层状地基分析的超级有限层法*

田管凤，汤连生

(1.中山大学地球科学系，广州 510275;2.中山大学应用力学与工程系，广州 510275;3.广东省地质过程与矿产资源探查重点实验室，广东广州 510275)

学者Cheung Y K［1］曾首先提倡采用有限层模型去逼近夹层板对全三维问题进行分析。之后，有限层法被应用于一般力系作用下的层状横向各向同性弹性连续地基的分析［2－3］。对于层状地基的良好适应性使有限层法得到进一步发展并应用于地基基础工程的分析。例如，在有限元法的基础上［4］，结合有限层法分析竖向荷载或倾斜荷载下的桩土共同作用以及箱形基础与横向同性土的共同作用［5－7］;建立三维横观各向同性土体固结的有限层法分析地基参数对地基沉降和固结性状的影响［8－9］;运用弹性黏弹性对应原理及拉氏变换给出黏弹性地基比奥固结有限层格式，分析地基蠕变变化规律［10］。在以上文献相关有限层法的计算理论中，选择的层元位移函数基本都是采用一次多项式与双重级数相乘的模式，本文暂且称之为传统有限层法。相关算例也表明了传统有限层法在求解多薄层 (薄层，指层元宽度与厚度的比值大于15;反之，为厚层)地基问题中得到比较满意的结果。然而，对于多厚层地基问题的有限层法分析暂未见有文献讨论。

本文着重从解决多厚层弹性地基问题出发，改进有限层元的位移模式，建立相应的一般有限层法。在此基础上，引入超级有限元思想，建立超级有限层法，以更好地适用于求解层状地基问题。

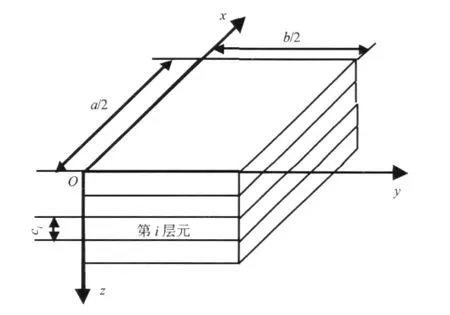
图1 有限层法计算模型Fig.1 Calculation model of finite layer method

1 6参数一般有限层法

1.1 物理模型

如图1坐标系中，有限体域的层状地基采用N层弹性均匀有限层元计算模型，矩形层元的平面尺寸a×b，图中所示为1/4层元。第i层元厚度为ci，i=1，2，….n。层元的四边采用简支约束，x= ±a/2边界上，y向水平位移v=0，竖向位移w=0;y= ±b/2边界上，x向水平位移u=0，竖向位移w=0。底板约束条件可按自由无支承、刚性光滑支承和刚性粗糙支承等情况分别考虑。

1.2 层元分析

1.2.1 6参数位移模式 结合有限层法基本原理［3］，考虑层元四边简支的边界条件，x、y、z三向位移u、v、w分别采用双重级数函数形式:

式中，a1i，mn、a2i，mn、a3i，mn(i=1，2，…，6)分别是位移u、v、w沿z方向变化的多项式系数。系数向 量 {aj}mn= {aj1，mn，aj2，mn，aj3，mn，aj4，mn，aj5，mn，aj6，mn}T，j=1，2，3。

在有限元法中选择位移模式时，常采用多项式的形式，其项数通常等于单元边界上的外结点的自由度数，过多过少都是不合适的。同样，在有限层法中，层元的自由度包含上下节点的三向位移共6个，因此式 (2)的竖向位移函数选择了包含6项的5次完全多项式。基于式 (1)、(2)建立的有限层法称之为6参数有限层法。

1.2.2 多项式系数的相关性分析 设层元应力向量 {σ}={σx，σy，σz，τxy，τyz，τzx}T;应变向量为{ε}={εx，εy，εz，γxy，γyz，γzx}T;则刚度矩阵［11］

式中，d1=E(1 － μ)/［(1+ μ)(1 － 2μ)］，d2=Eμ/［(1+ μ)(1 － 2μ)］，d3=E/［2(1+ μ)］，E 和μ为层元弹性模量和泊松比。

依据弹性体的静力平衡方程［12］，在暂时不考虑体力的条件下，有

将弹性层元的位移、应变、应力关系代入式(4)，整理得到

由于式 (4)及式 (5)对于任意x、y、z都必须成立，因此式 (6－1) ～ (6－3)对x、y一阶导数必然为零。将式 (6－1)(6－2)分别对x、y求导可得

对比式 (7－1)、(7－2)、(6－3)，由于x、y、z的任意性，三式中均含有相同的cos kmxcos kny项，则［kmF1(z)］、［knF2(z)］、［F3(z)］中的对应zi－1(i=1，2，…，6)项系数必需分别对应相同，才能保证三个方程的一致性收敛能够同时成立。从而推导得到系数向量{a1}mn、{a2}mn、{a3}mn间存在以下关系:

式中，矩阵 ［A2］mn、 ［A3］mn为多项式系数向量间的关系矩阵。可见，在层元位移模式的18个多项式系数中，由于其间存在相关性，实际独立的系数只有6个，正好与层元上下节面位移数目相同。

1.2.3 层元节面位移向量 设层元厚度为c，取其上下界面i、j节面的位移向量 {δ}mn=

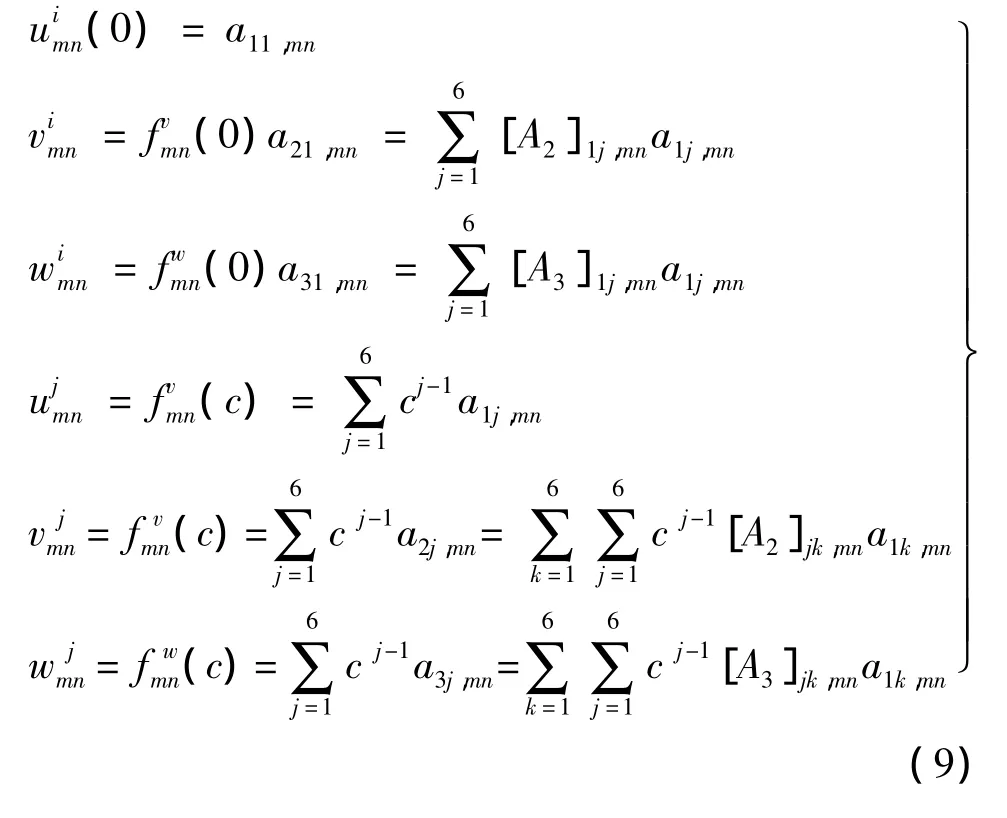
为基本未知量，则其 中， 矩 阵 ［R1］mn=， ［R2］mn=［A2］mn，［R3］mn= ［A3］mn，j=1，2，…，6。

1.2.4 层元刚度矩阵 据应变向量的定义可推导层元应变矩阵 ［B］mn，以及层元刚度矩阵 ［S］mnmn=［D］［B］mndV 的表达式。 ［S］mnmn的求解采用高斯－勒让德积分法。

1.2.5 层元等效荷载向量 以层元表面局部作用竖向均布力p为例，矩形面积形心位置 (x0，y0)，分布长度和宽度分别为l1、l2。则层元的等效荷载向量为

1.3 整体分析

设多层地基有限域中包含N个层元，可将层元刚度矩阵 ［S］mnmn顺序依次组装成3N+3阶整体刚度矩阵 ［K］mnmn和整体荷载向量 {F}mn。依据第N层元底面约束条件修改刚度矩阵［2］。如果底部采用自由条件，可作不处理。求解体系平衡方程即可得到各层元的节点位移参数向量 {δ}mn，经过m、n级数循环计算r×s次后叠加得到最后结果。当计算变量值的第三位有效数字不再随m、n值的增大发生变化而保持稳定作为级数收敛标准。

2 超级有限层法

2.1 超级有限层元模型

将层状地基作为单个或多个超级有限层元，单个超级层元包含多个小层元。如图2，在此超级层元内，第k小层元的界面分别为k和k+1，所在超级元内竖向局部坐标分别为 ξk和ξk+1。超级层元位移函数、节面位移向量、形函数等同2.2。

图2 超级有限层法计算模型Fig.2 Calculation model of super finite layer method

2.2 小层元与超级有限层元间的运算矩阵转换

设小层元k的上下节面位移

则根据超级有限层元的位移计算式，可得

式中，N'ij=Nij|z=ξk;N″ij=Nij|z=ξk+1，i=1，2，3;j=1，2，…，6。［A］mn为小层元与超级层元间的节面位移转换矩阵。

据超级有限元法的基本原理［13］，小层元相应于超级层元的转换刚度矩阵

转换荷载向量

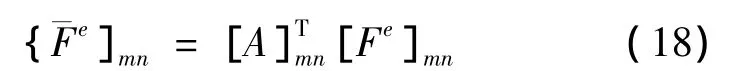
式中，［Se］mnmn和［Fe］mn分别为小层元的一般有限层刚度矩阵和荷载向量。

2.3 超级有限层元的集合与计算

单个超级有限层元的刚度矩阵和荷载向量是所含所有小层元的相应转换刚度矩阵和荷载向量}的依次迭加［13］。整个系统的运算矩阵按照所包含的超级有限层元在系统中的位置，按一般有限层法集合。根据整个系统平衡方程计算出超级有限层元的位移参数向量 {δ}mn后，小层元的位移、应变、应力可再经过矩阵转换求解得到。

以上基于6参数一般有限层法推导得到的超级有限层法，称之为6参数超级有限层法。

3 算例

有限层法的提出是为了解决竖向不均匀的层状地基问题。但是，为了验证本文中提出的6参数一般有限层法以及超级有限层法的有效性和准确性，有必要先将均匀弹性地基在不同情形下的位移或应力值与已有文献的解析解或数值解进行比较。

3.1 不同厚度的有限域地基单层计算

有限域单层地基采用均匀弹性的四边简支方板模拟，材料剪切模量G，弹性模量E，泊松比μ=0.3;方板边长a，板厚h=0.01 m，板的上表面满布均匀竖向荷载q=1 kPa，底面自由无约束。通过改变板的平面尺寸a，计算不同厚宽比h/a条件下板的上表面中心竖向位移w0及板底部中心的水平应力σx0。分别采用本文6参数一般有限层法与其他文献计算结果比较，见表1。

3.2 有限域地基的单层与多层计算

仍采用均匀弹性板模拟单层与多层有限域地基，板的各物理参数同3.1。将板厚h分单层和多层等不同情形，分别采用6参数一般有限层法、6参数超级有限层法计算w0及σx0，并与有限元法结果比较，见表2。

表1 不同厚度的有限域地基单层计算结果Table 1 Results of the finite single layer ground with different thickness

表2 有限域地基的单层与多层计算结果Table 2 Results of the finite ground of single-layer and multi-layer

3.3 半无限体地基计算

当采用有限层法计算的体域足够大时，可以近似为半无限体，用于求解半无限弹性地基的应力和位移。参考文献 ［2］，体域尺寸取水平方向L=B=20 m，厚H=12 m，底部采用刚性粗糙支承约束。弹性体材料常数E=5000 kPa，μ=0.3。均布方形荷载作用在体域表面中心，边长LQ=1 m，荷载集度p=1 kPa。分别采用分层和单层计算，结果见表3。

表3 半无限空间体表面中心的竖向位移Table 3 Vertical displacement of the surface centre of semi-infinite body

4 讨论

4.1 一般有限层法计算单层地基的合理性

据表1，对作用均布荷载的四边简支单层板中心处的表面竖向位移和底面水平应力值计算表明，6参数一般有限层法与已有文献的改进厚板解析解有良好的一致性［14］，位移和应力的误差范围分别小于2.5%、5.8%。说明6参数有限层法在用于计算厚层和薄层的单层地基具有合理性，为下文多层地基计算提供理论依据。然而，改进厚板解析解则只能对单板进行计算，显然不具备该优点。

根据有限层法层元分析，上下节面位移参数共有6个。本文提出的6参数位移模式，共含18个未知系数，即 a1i，mn、a2i，mn、a3i，mn(i=1，2，…，6)。但是，在应用弹性体静力平衡方程整理后发现，系数间存在如式 (8－1)(8－2)的相关性。这样，实际上独立的系数只有6个，其数目与层元节面位移数目完全对应，从而保证了有限层位移参数的完备性。据式 (1)，6参数位移模式包含了层元的刚体位移和常应变，即常数项和一次项;并且层元内位移连续，层元之间位移协调。这些条件保证了有限层法在双重级数计算时的收敛性。可见6参数有限层法这一半解析半数值法在弹性板分析中的有效性。

4.2 超级有限层法计算多层地基的合理性

据表2，采用单层和多层的不同方式，分别应用6参数一般有限层法和6参数超级有限层法，计算均布荷载下简支方板中心处的表面竖向位移和底面中心水平应力。通过将各种不同厚宽比的情形进行比较发现，在单层计算时，基于一般有限层原理推导得到的超级有限层法与一般有限层法的结果是完全一致的，除了计算程序中数值计算的些许误差之外。板表面中心位移计算结果与有限元法相比有很好的一致性，误差在0.12%～2.78%之间，进一步说明了6参数有限层法的合理性和准确性。然而，相比有限元法，超级有限层法不仅具有半解析法的计算数值准确的特点，而且具有层元网格简洁、计算快捷的优点。

在多层计算时，超级有限层法计算位移和应力结果与单层解有很好的一致性，误差都在0～1.26%之间。然而，一般有限层法的多层和单层计算比较发现，只有在h/a＜0.1时结果才一致;随着h/a增大，结果发生较大变化;在h/a=0.4时，多层计算位移值竟然达到单层计算值的10倍。因此说明，6参数一般有限层法仅适合于多层薄板计算。

应用有限层法的目的是为了适应地基的层状特点。如果将有限层法应用于均匀材料，则不管是采用多层还是单层的形式，结果都能达到很好的一致性，这样才能保证有限层法的有效性。

综合表1、表2算例结果，无论地基是薄层还是厚层，6参数超级有限层法都能很好的适应;而6参数一般有限层法则只适合于薄层地基分析。究其原因在于对层元间高阶变形的协调性要求的满足程度不同。一般有限层法中，层元间节面位移可以保证层元在节面处位移的连续协调性，但无法进一步保证层元之间位移的斜率等高阶变形的协调性，这样只有在薄层条件下比较适合采用。而超级有限层法，将所有小层元叠加为一超级层元，具有统一的超级层元位移函数，从而可以保证超级元内小层元间位移及其斜率等高阶变形的协调性，因此可以适用于多种厚度层元的计算。

4.3 有限层法计算半无限空间体的合理性

在采用有限体域模拟计算半无限空间体时，可以相对荷载作用面积，将有限的体域扩大进行近似计算。据表3，应用各种有限层法计算半无限空间体表面作用小面积荷载时的中心竖向位移与解析解比较。多层计算时，6参数超级有限层法接近Boussinesq解;而单层计算时，6参数有限层法和超级有限层法与Boussinesq解完全一致。说明6参数一般有限层法适用单层地基，而6参数超级有限层法则同时适用单层和多层地基。显然，超级有限层法可以解决布氏解所未能解决的层状地基问题。

4.4 级数收敛性确定

算例计算分析表明，达到收敛时的级数项m、n的取值主要受到荷载作用面积相对于体域尺寸大小不同的影响;而受层元的厚宽比h/a的影响较小。

在表1和表2中，表面满布均载的单层或多层有限域地基的计算结果都是在m和n均小于20时达到收敛标准得到的。但如表3中的小面积分布力作用时则需要计算较多项，计算位移结果在m和n接近50时才达到收敛标准。

此外，在表1和表2计算时发现，层元越薄(h/a越小)，收敛时需要的级数项m、n值越小。有的薄层 (h/a＜0.1)计算甚至在m=n=2时已达收敛。但即使层厚增大，m、n也未超过20。说明层元h/a对级数收敛性影响较小。因此，收敛稳定判断应以计算变量值相对稳定为标准。

5 结论

1)提出6参数一般有限层法，位移模式不仅满足了层元间的位移协调性，而且参数个数符合完备性要求。在用于单层地基分析时，位移和应力计算值与有限元解或解析解一致。然而由于不能满足层元间高阶变形的连续性，故仅适用于单层或多薄层地基;用于分析多厚层地基则误差较大。

2)提出6参数超级有限层法，既具有一般有限层法位移模式的完备性优点;同时满足超级层元内小层元间高阶变形的连续性，弥补了一般有限层法的不足。因此可以适用于各种厚度的单层和多层地基分析。

本文提出的超级有限层法对于层状地基分析的层数、层厚具有很好的适应性，将有利于层状地基理论的深入研究。

［1］CHEUNG Y K.结构分析的有限条法［M］.谢秀松，王贻荪，译.北京:人民交通出版社，1985:271－278.

［2］张问清，赵锡宏，宰金珉.任意力系作用下的层状弹性半空间有限层分析方法［J］.岩土工程学报，1981，3(2):27－42.

［3］宰金珉，宰金璋.高层建筑基础分析与设计［M］.北京:建筑工业出版社，1993:32－33.

［4］刘祚秋，温少荣，周翠英，等.桩、土、刚性承台相互作用下桩基内力计算新方法［J］.中山大学学报:自然科学版，2004，43(4):33－37.

［5］王旭东，魏道垛，宰金珉.群桩—土—承台结构共同作用的数值分析［J］.岩土工程学报，1996，18(4):30－36.

［6］赵明华，邹新军，邹银生，等.倾斜荷载下基桩的改进有限元—有限层分析方法［J］.工程力学，2004，21(3):129－133.

［7］肖仁成，赵锡宏.有限元和有限层元研究横向同性土对建筑物沉降的影响［J］.岩土力学，2007，28(10):2133－2137.

［8］梅国雄，宰金珉，赵维炳，等.横观各向同性土体三维比奥固结有限层解法［J］.中国工程科学，2004，6(7):3－47.

［9］梅国雄，宰金珉，赵维炳.横观各向同性土体有限层分析［J］.岩土力学，2005，26(2):225－230.

［10］夏君，梅国雄，梅岭，等.考虑固结的黏弹性地基的有限层法［J］.岩土工程学报，2009，31(3):437－441.

［11］郑颖人，孔亮著.岩土塑性力学［M］.北京:中国建筑工业出版社，2010:155－159.

［12］杨桂通.弹性力学［M］.北京:高等教育出版社，1998:12－15.

［13］曹志远，刘永仁，周汉斌.超级有限元法及其在结构工程中的应用［J］.计算结构力学及其应用，1994，11(4).

［14］钟正华，罗建辉.横观各向同性板的弹性理论和弹性改进理论及一种新的厚板理论［J］.应用数学和力学，1988，9(4):341 －354.

［15］王焕定，吴德伦.有限单元法及计算程序［M］.北京:中国建筑工业出版社，1997:190－191.