光子回波的求解及其应用*

陆龙钊，李 成，余向阳

(中山大学光电材料与技术国家重点实验室，广东广州 510275）

在非均匀展宽介质中，两个相隔一定时间的强短激光脉冲与共振吸收介质相互作用后，经过一定的时间后会自发辐射出一个光脉冲，这个光脉冲就是所谓的光子回波。光子回波是强短激光脉冲与物质近共振相互作用所产生的相干瞬态效应［1－2］。随着超短激光脉冲技术和量子光学理论处理方法的发展，人们对光子回波进行了深入的研究，并将其应用到了许多方面［3－4］。激光脉冲与物质的相互作用，在半经典理论框架下，可用 Maxwell－Bloch(MB)耦合方程描述［5］，其中Bloch方程描述在光场作用下的体系性质，Maxwell方程则描述了光场在体系中的特性。用Bloch矢量模型可对光子回波现象作出清晰的经典的唯象解释［2］，由此，可以较好地理解光子回波的物理机制。但要完全描述和理解光子回波物理图像并定量地给出光子回波信号的强度，则需要求解非均匀展宽体系的MB方程。MB只在某些特定的条件下，才能求得解析解，通常情形需要采用数值求解的方法，均匀和非均匀展宽体系MB方程数值算法都已经得到了很好的研究［6－11］。本文在非均匀展宽体系 MB方程数值解

1 基本理论

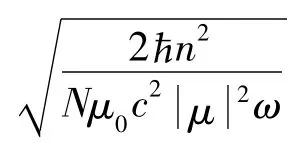
在薄样品近似下，可只考虑光场对体系的作用，而忽略光场在介质中的传播效应，因此光场不再随时间变化，这就可将坐标转到入射光场前进的坐标系中，由式 (1－d)可得薄样品后边界的光场为

由上式可见，对已知线型函数g(Δ)的介质，求出v后，便可求出光作用于介质后的光场强度，显然该光场强度与样品的厚度L成正比。v可由方程 (1－a)～(1－c)，即Bloch方程求得，这是一组非线性常微分方程，这里采用文献 ［7］所建立的校正四阶龙格－库塔 (RK4)法进行数值求解。这样，由 (2)式就可计算薄样品近似下光子回波信号的强度。而光子回波的唯象解析也是基于薄样品近似在Bloch矢量模型上得出的。

通常，实现光子回波的实验样品都是有一定厚度的吸收介质，光场在通过吸收介质时，介质厚度必然会强烈影响光场的传播特性［11－12］。因而对实际实验条件下的光子回波的特性而言，薄样品近似虽然可以解析一些现象，但显然不是一个很好的近似。当考虑样品的厚度时，求解 MB耦合方程(1)，才能得到体系与光场的性质，方程 (1)是一组非线性偏微分－积分方程，其求解是复杂的，这里我们在前期工作的基础上，采用文献 ［10］所建立的“预报 －校正四阶龙格 －库塔(PCRK4)”法建立了厚样品光子回信号强度的求解方案。当初边界条件已知时，就可计算厚样品中光子回波信号的强度。

2 计算结果与讨论

数值计算求解方程 (1)的初始条件为:

边界条件为初始入射脉冲，假定脉冲为高斯型的，则有

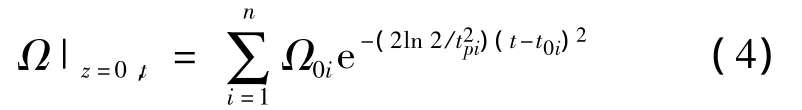
介质的非均匀展宽线型g(Δ)假定为高斯型，其归一化的形式为

式中，Δd为半高宽。

2.1 二脉冲光子回波

两个相隔时间为t1=t02－t01的强短激光脉冲与共振吸收介质相互作用后，经过t1的时间后会观测到由介质自发辐射出的一个光脉冲，这就是二脉冲的光子回波。薄样品近似下双脉光子回波信号，在特定条件下，经过适当的近似，可得到回波信号的解析解［13］，虽然解析解可以很好解释光子回波形成的物理机制，但只能给出半定量的结果。为了定量给出光子回波信号的强度，就需要采用数值方法进行求解，以便更深入而全面地描述光子回波的形成机制及影响信号强度的因素。

图1显示了共振 (Δ=0)且忽略了驰豫时间(Γ1=0、Γ2=0)时，薄样品近似下二脉冲光子回波信号的强度。计算时各参数为:L=1，tp1=tp2=1，Δd=3，t01=5，t02=15，S01=π/2，S02=π。图1中点线是输入光脉冲 (z=0)的强度，实线是样品后边界处 (z=L)光场的强度。从图中可以看出:在第二个脉冲作用后，经过t1时间间隔，出现了光子回波。这个结果与解析解及矢量模型［5］分析是一致，也说明了所建立的数值算法是可靠性。

图1 光学薄样品中的二脉冲光子回波Fig.1 A two－pulse photon echo in optically thin media

虽然解析解的结果可以得到二脉冲光子回波强度以及退相时间对光子回波强度的影响，但MB方程中的其它参数，诸如失谐量、驰豫时间、非均匀展宽线宽以及激发脉冲的强度等，对光子回波信号强度的影响是解析解所不能完全给出的，而用数值求解的方法，可以计算各种参数对光子回波信号强度的影响。

图2(a)显示了退相时间T2对光子回波信号强度的影响。从图中可以看出光子回波信号的强度随着T2的增大而迅速增大，当T2大过一定值后光子回波强度增加变慢，最后趋向于平缓。这是由于T2越小，退相过程就越快，经过第二个脉冲作用后偶极矩相位能够反向趋于一致的数目越少，因此光子回波的强度就较小;反过来，T2越大，退相过程越慢，偶极矩相位能够反向趋于一致的数目越多，因此光子回波强度就较大。当T2≥t1时，在t1时间内T2对退相过程的影响可以忽略，光子回波强度趋于定值。光场载波频率与共振频率的失谐也会影响光子回波的强度。图2b给出了失谐量对光子回波强度的影响。从图中可以看出:失谐量绝对值越大，光子回波信号的强度越低，整个曲线以Δ=0为对称分布，说明正、负失谐的影响是相同的。

图2 退相时间 (a)失谐量 (b)对光子回波强度的影响Fig.2 Peaks of echo power for different transverse

图3显示了厚样品的光子回波强度的三维图，计算的参数与图1相同。从图中可以看出，两个入射脉冲的强度随介质厚度的增加而减小，光子回波信号的强度则随介质厚度的增加先增大后减小，这意味着实现最强的光子回波与介质的厚度的选取有关。在时间坐标上，光子回波出现的位置与薄样品近似下是相同的。

图3 光学厚样品中的二脉冲光子回波Fig.3 A two－pulse photon echo in optically thick media

2.2 三脉冲光子回波

在三脉冲作用下，光子回波的特性变得复杂，已无二脉冲光子回波那样清晰的物理图像。三脉冲光子回波也被称为受激光子回波。其中，第一个输入脉冲称为“写”脉冲，它的作用是实现介质中原子基态与激发态间的相干;随后输入的第二个脉冲称为“数据”脉冲，它的作用是将相干性传递给基态与激发态间频率依赖的“数据”脉冲，此时“数据”脉冲的信息也被存储在介质中;然后在某个时刻输入第三个脉冲，称之为“读”脉冲，这个脉冲的作用是激发光子回波［14］。

图4是在薄样品近似下，三脉冲光子回波的计算结果。三个脉冲的入射脉冲面积分别为S01=π/2、S02=0.1π和S03=π/2，脉冲的时间间隔为t1=t02－t01=10和t2=t03－t02=20，其他计算参数与图1相同。从图中可以看出，在第三个入射脉冲作用后，经过时间t1后会出现一个脉冲，这个脉冲称为受激光子回波。

图4 光学薄样品中受激光子回波Fig.4 A stimulated photon echo in optically thin media

图5给出了厚样品中的受激光子回波强度的三维图，除样品空间参数外，所选其它参数与图4同。从图中可以看出，三个入射脉冲的强度随介质厚度的增加而逐渐变小，光子回波强度随介质厚度的增加先增大后减小，其它性质与薄样品近似下受激光子回波的特性是一致的。受激光子回波携带了第二个输入脉冲，即数据脉冲的信息，这一点在多脉冲光子回波中会体现的更明显。

图5 光学厚样品中受激光子回波Fig.5 A stimulated photon echo in optically thick media

2.3 多脉冲光子回波

图6显示了多脉冲入射时所产生的光子回波，写脉冲的面积为0.5π，每个数据脉冲的面积为0.025π(组成编码11101101)，读脉冲的面积为0.5π，写脉冲与第一个数据脉冲间的时间间隔为20，最后一个数据脉冲与读脉冲间的时间间隔为70。从图中可以看出，薄样品近似下光子回波所携带的信号编码与数据脉冲的编码完全相同［15］，读出时间间隔与写入时间间隔一致。图7给出了厚样品中多脉冲入射的情况下的光子回波的计算结果。

图6 光学薄样品中多脉冲光子回波Fig.6 A multiple－pulse photon echoes in optically thin media

图7 光学厚样品中多脉冲光子回波Fig.7 A multiple－pulse photon echoes in optically thick media.

如果将二脉冲入射情况下的第一个脉冲改成多个数据脉冲 (每个“数据”脉冲的面积为0.025π， “读”脉冲为 π)，组成编码11101101，则得到的光子回波如图8所示。此时最后一个“数据”脉冲与“读”脉冲间距，与“读”脉冲与第一个光子回波间距相同，这个性质与二脉冲光子回波相同，并且光子回波所对应的编码为10110111，与数据编码顺序正好相反。

编码数据的存储与读取在时间轴上是满足一定规律的:图7显示编码数据的存储与读取与受激光子回波脉冲间隔一致，而图8给出的编码数据存储与读取与二光子回波脉冲间隔一致，都可用于实现光脉冲信号的存取。编码数据脉冲光子回波的这种特性，是实现光脉冲数据存储与读取的有效方式之一。

图8 光学厚样品中多脉冲光子回波Fig.8 A multiple－pulse photon echoes in optically thick media

3 结论

光子回波信号的数值解法是在非均匀展宽二能级体系MB耦合方程数值算法的基础上建立的。在光学薄样品近似条件下，数值计算了二脉冲光子回波与三脉冲光子回波，与解析解的结论是一致的，表明所建立数值解法是可靠性的，并讨论了弛豫时间对光子回波信号的影响。进一步计算了厚样品情况光子回波信号，讨论了介质厚度对光子回波强度的影响，结果表明光子回波的强度随介质厚度的增加先增大后减小，这意味着有最佳的介质厚度实现最强的光子回波信号。编码数据脉冲的光子回波是实现光脉冲数据存储与读取的有效方式之一，并满足一定的规律。本文就存取时间间隔、编码顺序等进行了初步研究，对编码数据脉冲光子回波的更深入的研究，诸如实现多比特编码数据脉冲的有效可靠存取等，将在后续工作的进行更深入的研究。

［1］KURNIT N A，ABELLA I D，HARTMANN S R.Observation of a photon echo［J］.Phys Rev Lett，1964，13:567.

［2］ABELLA I D，KURNIT，HARTMANN S R.Photon echoes［J］.Phys Rev，1966，141:391.

［3］BOYE D M，FEOFILOV S P，MELTZER R S.Two－pulse photon echo studies of optical dephasing in CaF2:Eu2+［J］.J Lumin，1998，76/77:60 －63.

［4］OLSON R W，LEE H W，PATTERSON F G，et al.Optical density effects in photon echo experiments［J］.J Chem Phys，1982，76(1):31 －39.

［5］ALLEN L，EBERLY J H.Optical resonance and two－level atoms［M］.New York:Dover，1987.

［6］余向阳，周建英.飞秒相干瞬态过程的Bloch方程描述［J］.中山大学学报:自然科学版，1999，38(2):24－27.

［7］郭莹莹，余向阳.光学Bloch方程的数值解法［J］.中山大学学报:自然科学版，2005，44(5):108－110.

［8］蒋月，余向阳.二能级体系Maxwell－Bloch方程的数值求解及其应用［J］.中山大学学报:自然科学版，2007，46(s2):176－179.

［9］张华荣，蒋月，李成，等.均匀展宽介质中激光超短脉冲面积的演化规律［J］，光子学报，2009

［10］李成，张华荣，余向阳.非均匀展宽体系Maxwell－Bloch方程的求解［J］.中山大学学报:自然科学版，2009，48(4):36 －41.

［11］YU X Y，LIU W，LI C.Near－resonant propagation of short pulses in a two－level medium［J］.Phys Rev A，2011，84:033811.

［12］AZADEH M，CORNISH C S，BABBITT W R，et al.Efficient photon echoes in optically thick media［J］.Phys Rev A，1998，57:4662.

［13］TSANG L，CORNISH C S，BABBITT W R.Analytic solutions of the Maxwell– Bloch equations for high photon－echo efficiency of multiple pulse sequences［J］.J Opt Soc Am B，2003，20:379.

［14］STAUDT M U，HASTINGS－SIMON S R，NILSSON M，et al.Fidelity of an optical memory based on stimulated photon echoes［J］.Phys Rev Lett，2007，98:113601.

［15］LUO B，ELMAN U，KRÖLL S，et al.Amplification of photon echo signals by use of a fiber amplifier［J］.Opt Lett，1998，23:442.