列主元SVD-QR方法修剪策略参数调整的D-FNN算法研究*

张德丰，马子龙

(1.佛山科学技术学院计算机系，广东佛山 528000;2.哈尔滨工业大学电子工程系，黑龙江哈尔滨 150001）

模糊神经网络控制在控制领域里目前已经成为一个研究热点，把神经网络应用于模糊系统，可以解决模糊系统中的知识抽取问题;把模糊系统应用于神经网络，神经网络就不再是黑箱了，人类的知识就很容易融合到神经网络中。将模糊系统与神经网络适当地结合起来，吸取两者的长处，则可组成比单独的神经网络系统或单独的模糊系统性能更好的系统。由于二者既有共性又有互补性，将两者有机地结合起来，发挥各自的优势，是智能控制领域研究的主要方向和发展趋势之一。

1 算法的理论分析与确定

1.1 列主元SVD-QR方法修剪策略

修剪技术对于动态时变非线性系统的辨识是非常必要的。如果在学习进行时，检测到不活跃的模糊规则并加以剔除，则可获得更为紧凑的D-FNN结构。在本文中我们将采用列主元SVD-QR方法作为一种修剪技术来选择重要的模糊规则。

列主元SVD-QR方法最初由Golub等［1］提出，以解决回归分析中的子集选择问题，在本文中用这种方法从给定的规则库中提取最重要的模糊规则。这种方法的基本思想是用H(b)θ(b)替换如下线性回归问题中的Hθ

其中，H(b)∈Rn×b由H的b个列构成，这b个列在H中的位置决定了用规则库中哪些规则来逼近向量D。

假设H∈Rn×v的SVD有式H=U∑ST给定，并且通过式 (2)来定义矩阵

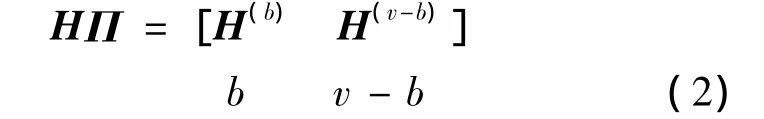
其中，Π∈Rv×v是一个交换矩阵。Golub等人证明［2］:如果

其中，σb(H(b))和σb(H)分别为H(b)和H的第b个奇异值。

这个结果表明，为了获得充分独立的列子集，即对应于模糊规则中最重要的子集，交换矩阵Π的选择使得产生的S'11子矩阵应不是病态的，从而‖(S'11)－1‖2尽可能地小。这意味着计算的子集H(b)趋向于使它的最小奇异值σb(H(b))最大化［3］。解决这个问题可以采用Golub等人提出的方法，即通过计算矩阵列主元的QR分解来解决［4］，其中∈和∈由下式来定义:

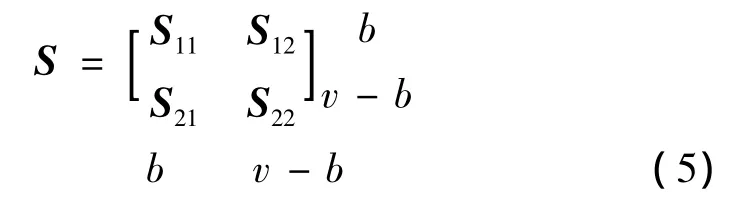
特别地，如果用列主元的QR分解来计算［5］:= ［R11R12］b v－ b (6)其中，Q∈Rb×b是正交矩阵，Π∈ Rv×v是交换矩阵，且R11∈Rb×b是上三角矩阵，则式 (3)意味着:

注意到 R11为非奇异，而且 ‖(S'11)－1‖2=。因此列主元法可产生一个非病态的R11和S'11。

矩阵Π的每一列只含有一个“1”(其他的元都为0)。“1”在Π中的位置决定了H的列在HΠ中的位置及其在规则库中的位置。为了说明这个问题，假设

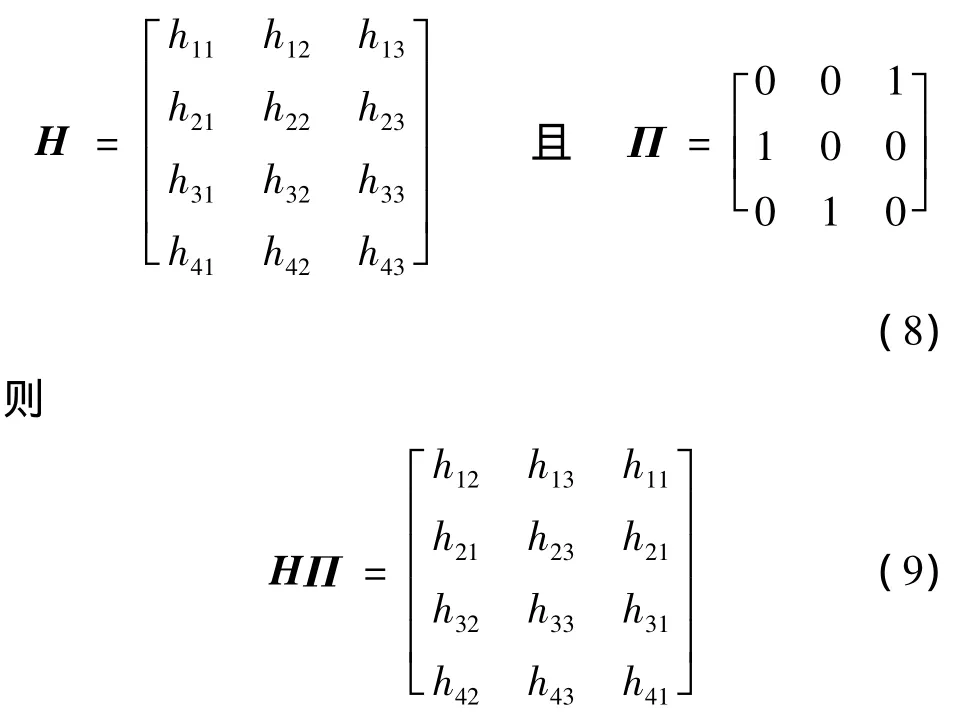
如果想用两条模糊规则建立一个模型，则应该选择第二和第三个规则［6］。

b个最重要的模糊规则的候选者可以通过求解如下简化方程得到:

其中，θ(b)= ［θ1，θ2，…，θb］T且 H(b)需要像前面一样通过使用b个最重要的模糊规则进行归一化处理［7］。

列主元的SVD-QR方法可以归纳成如下几个步骤:

1)计算H的SVD，也即H=UΣST同时保存Σ和S。

2)检查 Σ =diag(σ1，σ2，…，σv)中的奇异值，确定用来构建模型的模糊规则数 b，其中 b≤rank(H)。

4)基于b个最重要的模糊规则构造归一化矩阵 H(r)∈ Rn×b

5)用SVD方法求解H(b)θ(b)=D得到θ(b)。

SVD-QR算法不需要明确地构造相关矩阵，因此，避免了不必要的数字和舍入误差。此外，众所周知，与特征值相比，奇异值的计算更有效，且具有更高的数值计算稳定性。因此，从应用的角度来看，SVD-QR算法优于ED(特征值分解)算法［8］。

1.2 D-FNN参数调整方法

卡尔曼滤波 (Kalman filter，KF)算法可以用于结果参数调整。本文中，我们还选择扩展的卡尔曼滤波方法 (extended Kalman filter，EKF)来调整这些参数。作为一种非线性更新算法，EKF方法可以用来调节D-FNN的所有参数。由于全局的方法将涉及大矩阵运算，遇到巨大计算负担以及占用大量的内存，因此，这种全局方法可以被划分为一系列可处理的子问题。在实际应用中，可以用卡尔曼滤波 (KF)方法来调节结果参数，同时，EKF方法用于更新前提参数的中心和宽度，从而使得所有参数都被修正。这一思想等价于把全局算法分解为一系列解耦的算法［9］。

图1所示为EKF用于D-FNN参数调整的原理图。实验结果表明，高斯中心对系统性能影响不大，因此只对高斯宽度进行更新。

图1 EKF用于D-FNN参数调整的原理图Fig.1 EKF for D-FNN parameter adjustment principle diagram

结果参数的更新是线性的，而高斯宽度的更新是非线性的，可以用EKF作如下优化:

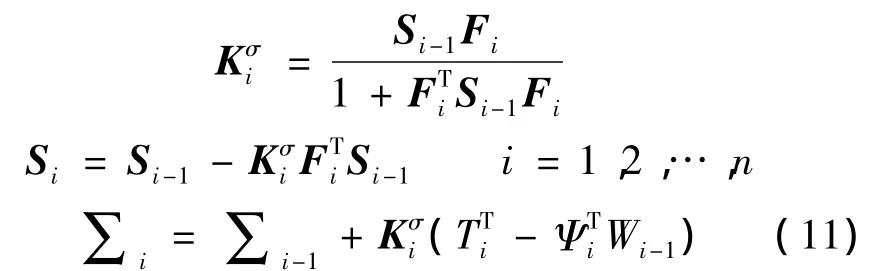
初始条件为∑0＞0以及S0=ρI，其中，ρ为一个小的正数，是i第次观测的增益矩阵，Si是第i次观测误差协方差矩阵，∑i=(σ1，σ2，…，σu)表示经过i次迭代后的高斯宽度向量，Fi=(δσ1，…，δσj，…，δσu)是第 i次观测宽度的梯度向量。

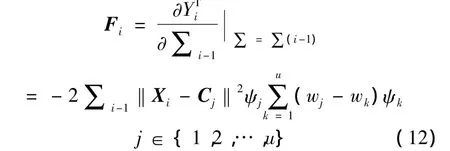
其中，Cj和wj分别是中心和第j个RBF单元的权值，ψj是第 j个归一化层的输出［10］。

需要强调的是，KF或EKF算法用于D-FNN，当一条规则产生/去除或者宽度有任何的调整时，将产生额外的计算负担，即在这些情况下，迭代将必须从第一个样本开始。

2 实验结果与分析

在本文中，我们的目的是验证采用列主元SVD-QR方法修剪策略与卡尔曼滤波方法来调整这些参数的D-FNN系统能否逼近一个动态而且是时变的系统，通过药物注射系统的直接逆控制来验证我们所采用算法的有效性。

当D-FNN在药物注射系统中作为控制器时，我们的目标是得到适当的控制行为u(t)，使输出值y(t)逼近期望值r(t)，为了实现这个目标，涉及到学习和应用两个阶段。在学习阶段，潜在对象的时变动态逆模型被D-FNN辨识，然后，D-FNN在应用阶段作为控制器产生控制行为［11］。

逆模型通常由式 (13)表示的NARX模型经过简单推导得到式 (14):

由式 (14)可以看到u(t)的产生还需要知道未来的值y(t+1)。为了克服这个问题，通常用r(t+1)代替y(t+1)。这个假设是合理的，因为r(t)与参考信号有关，通常被称为前一步［12］。

而另一个问题是逆映射f－1是否一直存在?这里暂不考虑式 (14)中的逆模型是否存在，可以用NARX模型直接构造如下的逆模型:

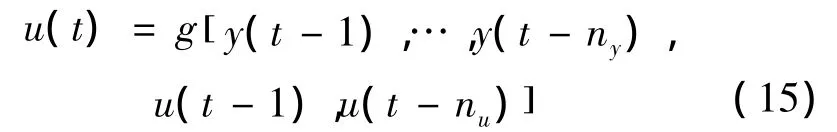
从而g≈f－1。应当指出，在物理意义上g不是f的准确逆模型，它只是数学上逼近这个逆映射［13］。

一般的病人响应模型描述如下［14］

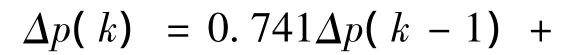
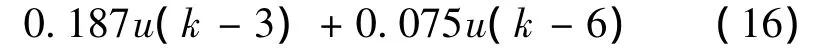
为了产生训练数据，药物注射率u(k)取为:

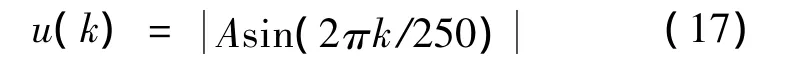
设A=50，初始条件为:当t≤0时，Δp(t)=0，u(t)=0，根据式 (16)和式 (17)提取200个样本。式 (16)的逆模型取为:

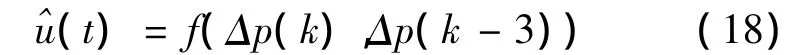
其中，f是D-FNN，它代表式 (16)的逆映射。基于列主元SVD-QR方法参数调整的D-FNN控制器训练的结果如图2所示。

图2(a)是训练阶段的输出误差;图2b是训练阶段的均方根误差;图2(c)是训练阶段期望和实际的注射率;图2(d)是训练阶段期望与实际注射的误差。

图2 训练阶段参数变化模型训练结果Fig.2 Training phase parameter changes in model training results

然后，把训练好的D-FNN用于控制对象。假定采样时间是15 s，病人初始的血压设为140 mm-Hg(1 mmHg=133.322 Pa)，最后的血压要求降低到100 mmHg，如图3a所示。如果期望的血压变化中含有方差为1 mmHg的白噪声，如图3b所示。图3c显示了在噪声环境下的血压误差，药物注射率和血压之间的关系如图3d所示。由仿真结果可以看到血压随着药物注射的变化而平稳地变化，并没有明显的延迟，这表明D-FNN对系统进行了很好的建模。仿真的结果如下:

血压变化量 Δpmax=5.91;平均动脉血压MAPmin=97.3;平均动脉血压变化量ΔMAPmax=2.63

由上述仿真结果可以看到:血压的变化很好地满足了药物注射系统的约束条件。

为了跟踪模型的时变特性，对一种参数和结构都随时间变化的复杂时变系统进行仿真。D-FNN的性能根据Δpmax和 RMSE进行了评估，结果如表1所示。

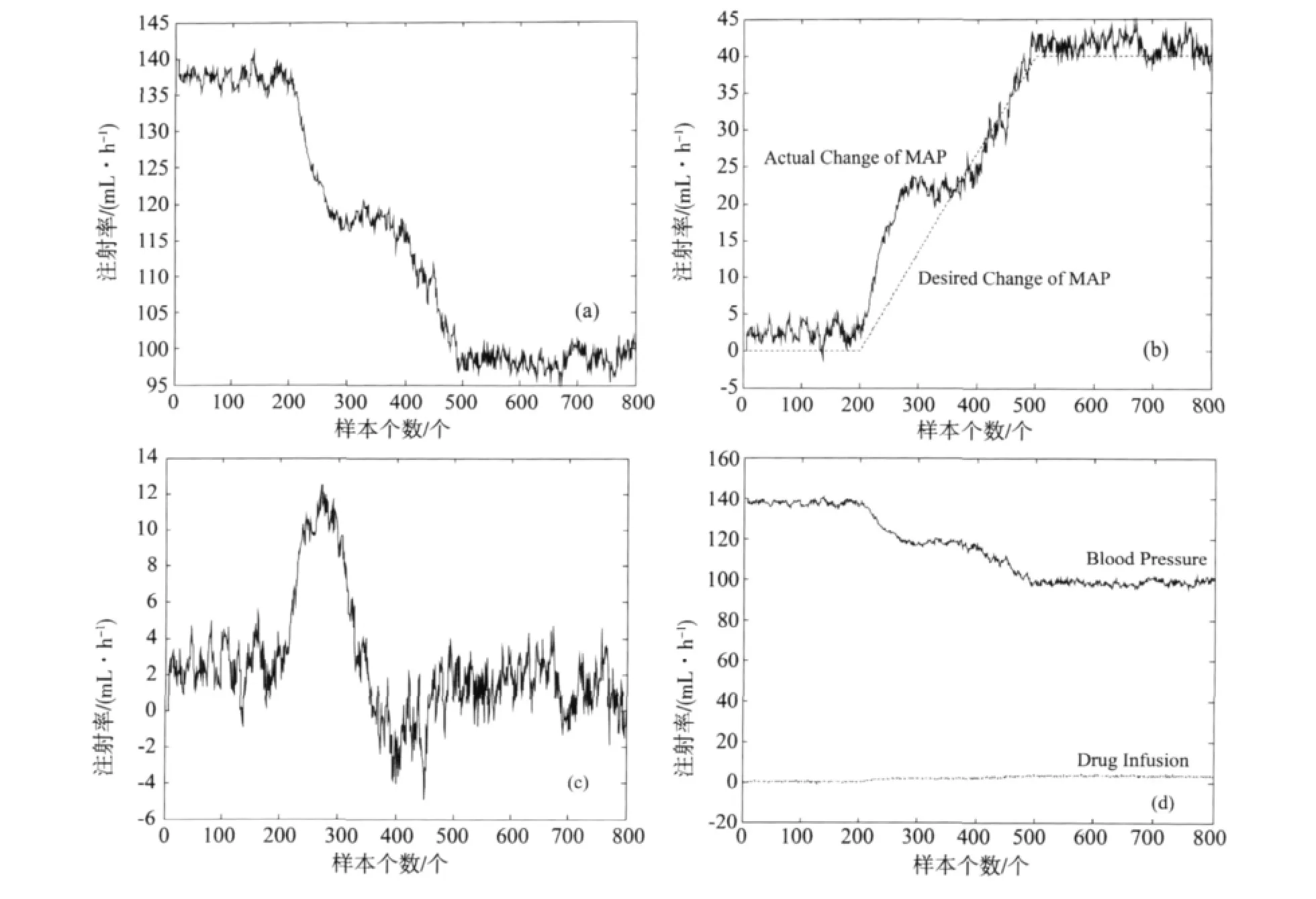
图3 测试阶段参数变化模型测试结果Fig.3 Parameter changes in the model test results of the testing phase

表1 D-FNN控制器的性能Table 1 The performance of the D-FNN controller

文献 ［15］中的结果列于表2中。与文献［15］的方法 IANC相比，我们的测试结果 (图3d)非常稳定，即使在噪声环境下也没有大的振荡。D-FNN控制器的性能根据期望和实际MAP变化的最大误差 Δpmax来评估，同时，与文献 ［15］相比较的结果列于表2中。

表2 IANC与D-FNN的性能比较Table 2 Performance comparison of IANC with D-FNN

从仿真结果来看，由于使用了列主元SVD-QR方法修剪技术，规则数很快达到稳定，使得网络结构没有持续增长，避免了过拟合及过训练现象，因而确保了系统的泛化能力。

考虑系统作为时变结构，从表2、图3d来看，仿真结果表明D-FNN控制器具有良好的性能，没有出现明显的延迟和震荡，这也表明D-FNN很好地学习了模型特性，也说明D-FNN控制器优于文献 ［16］的方法。

3 结论

一个规则可能最初是活跃的，但逐渐对系统几乎没有贡献了。因此，修剪技术对于动态时变非线性系统的辨识是非常必要的。如果在学习进行时，检测到不活跃的模糊规则并加以剔除，则可获得更为紧凑的D-FNN结构。可以用KF方法来调节结果参数，同时，EKF方法用于更新前提参数的中心和宽度，从而使得所有参数都被修正。EKF是基于在线的学习算法，该算法可用于平滑、滤波或者预测非线性动态系统的状态，同其他基于梯度的在线算法相比，EKF可以加快收敛速度。仿真结果表明，由于使用了列主元修剪策略与参数调整算法使得D-FNN具有更紧凑的系统结构、强大的泛化能力以及快速的学习速度。

［1］PLATT J.A resource-allocating network for function interpolation［J］.Neural Computation，2007，19(2):213－225.

［2］BRUNELLI R，POGGIO T.Face recognition:features versus templates［J］.IEEE Trans Pattern Analysis and Machine Intelligence，2010，25(10):1042－1053.

［3］马莉，张德丰，马子龙.滑动窗与修剪技术的动态模糊神经网络方法研究［J］.中山大学学报:自然科学版，2010，49(1):48－52.

［4］HONG Z.Algebraic feature extraction of image for recognition［J］.Patt Recog，2009，24(2):211 －219.

［5］TURK M A，PENTLAND A P.Eigenfaces for recognition［J］.Cognitive Neuroscience，2008，3(1):71 －86.

［6］WANG L X，MENDEL J M.Fuzzy basis function，universal approximation，and orthogonal least squares learning［J］.IEEE Trans Neural Networks，2009，3:907 －914.

［7］EICKELER S，MUELLER S，RIGOLL G.High quality face recognition in JPEG compressed images［C］.Proc IEEE Int Conf Image Processing，2008:672－676.

［8］WU S Q，ER M J.Dynamic fuzzy neural networks:a novel approach to function approximation［J］.IEEE Trans Syst Man Cybern Part:B，2010，30:358 －364.

［9］LU Y，SUNDARARAJAN N，SARATCHANDRAN P.A sequential learning scheme for function approximation by Using minimal radial basis function networks［J］.Neural Computation，2009，19(2):461－478.

［10］任爱红.模糊随机过程函数列均方差一致Henstock积分的可积性［J］.中山大学学报:自然科学版，2010，51(4):41－44.

［11］CHELLAPPA R，WILSON C L，SIROHEY S.Human and machine recognition of faces:a survey［J］.Proc IEEE，2009，93(2):705 －740.

［12］VALENTIN D，ABDI H，O’Toole A J，et al.Connectionist models of face processing:a survey［J］.Patt Recog，2009，27(4):1209 －1230.

［13］JANG J-S R.ANFIS:adaptive-network-based Fuzzy inference system［J］.IEEE Trans Syst Man Cybern，1993，23(3):665－684.

［14］KADIRKAMANATHAN V，NIRANJAN M.A function estimation approach to sequential learning with neural networks［J］.Neural Computation，2008，16(4):954－975.

［15］POLYCARPOU M M，CONWAY J Y.Indirect adaptive nonlinear control of drug delivery systems［J］.IEEE Trans Automat Contr，2010，43:849 －856.

［16］BEHBEHANI K，CROSS R R.A controller for regulation of mean arterial blood pressure using optimum nitroprusside infusion rate［J］.IEEE Trans Biomedical Engineering，2010，47:513 －521.