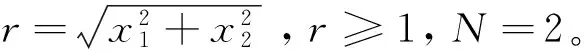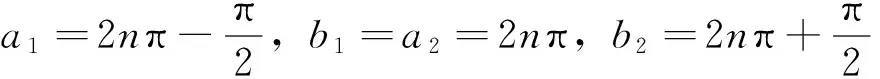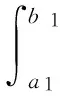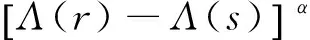二阶非线性椭圆型微分方程新的振动准则
林全文,庄容坤
(1. 广东石油化工学院数学系,广东 茂名 525000;2. 惠州学院数学系, 广东 惠州 516007)
考虑如下二阶非线性椭圆型微分方程
▽·(A(x)▽y)+q(x)f(y)=e(x),x∈Ω
(1)

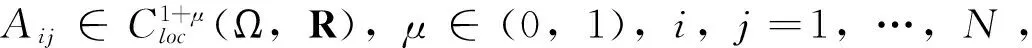
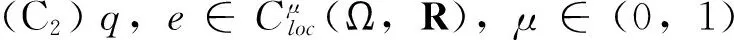
(C3)f∈C1(R,R),且对所有y≠0,yf(y)>0,f′(y)≥K>0,K为常数。

偏微分方程的振动理论一直受到众多学者的关注。对于如下拟线性椭圆型微分方程
▽·(A(x)▽y)+q(x)f(y)=0
(2)
Noussair 和Swanson[2]利用如下偏Riccati变换
(A▽y)(x)
(3)
将Wintner型定理推广到方程(2),其中α∈C2为正函数。Swanson 在文献[3]中总结了方程(2)在1979年以前的振动结果。有关方程(2)的最新的一些研究结果请读者参阅文献[4-7]及其所列的参考文献。最近作者在文献[8]中利用偏Riccati 变换技巧及H(r,s)型函数,获得方程(2)的若干振动准则,其中的一个结果可以表述如下:
定理A 假设f(y)/y≥K|y|y-1,y≠0,K>0,v>1。令
其中Sr={x∈RN:x=r},r> 0, dσ表示RN中球面积分元,ωN表示RN中单位球面表面积。若limr→∞Λ(r)=∞, 且对每个T≥a0,下面的条件成立:
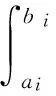
(A1) 存在T≤a1 且q(x)≥0(不恒等于零),x∈G(a1,b1)∪G(a2,b2); (A2) 存在ci∈(ai,bi),i= 1, 2,使得T≤a1 (4) (5) 则方程(1) 是振动的。 2006年,Yang[9]在对双曲型偏微分方程的振动性的研究中,引入新的核函数H(r,s,l),得到若干新的Kamenev型振动准则。受此工作及Philos[10], Kong[11]等工作的启发,本文定义如下函数集R。 定义1 令E0={(r,s,l):0≤a0≤l (H1)H(r,r,l)=0;H(r,l,l)=0,r>l≥a0,且H(r,r,l)>0, (r,s,l)∈E0。 (H2)H(r,r,l) 在E对第二变元存在连续的偏导数且存在函数h∈C(E0,R)使得 定义2 令D= {(r,s):r≥s≥a0},D0={(r,s):r>s>a0},H1和H2∈C1(D,R)。 称函数对,如果存在h1和h2∈C1(D0,R)满足下列条件: (H3)Hi(r,r) = 0,r≥a0且Hi(r,s)>0,∀(r,s)∈D0,i=1,2; 将上面定义的新型函数作为核函数,建立方程(1)的若干新的振动准则。这些振动准则比现有的结果具有更高的一般性,并能得到方程(1)的解的零点分布的一些信息。 为方便起见, 我们引入如下记号 其中Sr={x∈RN:x=r},r>0,dσ表示RN中球面积分元,ω为RN中单位球面积。K为条件(C3)中的常数。 定理1 假设对任意的T≥a0, 存在T≤a1 (6) 如果存在H∈R 使得 (7) 对i= 1或i= 2成立。则方程(1) 是振动的。 证明若不然,不失一般性设方程(1)存在非平凡解y(x) 使得y(x)>0,x≥T≥a0。 定 义 (A▽y)(x),x∈G[T,+∞) (8) 和 (9) 由方程(1) 及(8)式,可得 (10) 其中WT为W的转置。 对V(r)求导并利用Green公式得,得 (11) 再由(11)式及(9)式,得 (12) 由假设知,可选取a1,b1≥T,使得e(x)≤0,x∈I1=Ga1,b1(a1 (13) 将(13)式的变量r改为s,并两边同乘以H(bi,s,ai)再从ai到bi(bi≥ai≥T) 积分得 (14) 即 这与假设(7)矛盾。定理1证毕。 在定理1中取H(r,s,l)=H1(r,s)H2(s,l),其中(H1,H2)∈Ξ, 经简单的计算,可得如下结论。 定理2 假设对每个T≥a0,存在T≤a1 (15) 对i=1或i=2成立。则方程(1)是振动的。 在定理2中若取H1= (r-s)α,H2=(s-l)β,α,β>1, 则可得如下结论。 定理3 假设对每个T≥a0,存在T≤a1 (16) 对i=1或i=2成立。则方程(1) 是振动的。 定义 在定理2中取H1=[Λ(r)-Λ(s)]α,H2=[Λ(s)-Λ(l)]β, 其中α,β>1, 可得如下振动准则。 定理4 假设对每个T≥a0,存在T≤a1 (17) 对i=1或i=2成立,则方程(1) 是振动的。 (18) 对i=1或i=2成立,则方程(1) 是振动的。 证明注意到 (19) 由(18)-(19)式,得 (20) 由(18)式,(20)式得 上式蕴含(17)式当α,β分别用2α和2代替时(17)式成立,从而由定理4知,方程(1) 是振动的,定理5证毕。 类似分析可得如下定理。 (21) 对i=1或i=2成立。则方程(1) 是振动的。 例1 取η1>η2>0,则下面的非线性椭圆型微分方程 (22) 是振动的,如果 γ(-12π2-144π+576)-η1π3>0 取K=1,则 g(r) =ωλ(r)rN-1= 2πη1 对a2,b2类似可得 由定理3知方程(22) 是振动的。 注1 由于引入新的核函数H(r,s,l),在特殊情况下该核函数可选取为Philos型振动准则的核函数的积H1(r,s)H2(s,l),因而定理1-6 是新的。 参考文献: [1] GILBAG D, TRUDINGER N S. Elliptic partial differential equations of second order [M]. New York: Spinger-Verlag, 1983. [2] NOUSSAIR E S, SWANSON C A. Oscillation of simlinear elliptic inequalities by Riccati transformation [J]. Canad J Math, 1980, 32(4): 908-923. [3] SWANSON C A. Semilinear second order elliptic oscillation [J]. Canada Math Bull, 1979, 22: 139-157. [4] XU Z T. Riccati techniques and oscillation of semilinear elliptic equations [J]. Chin Ann of Math, Ser A, 2003, 24(5): 565-574. [5] XU Z T. Oscillation and nonoscillation of solutions of second order damped elliptic differential equations [J]. Acta Mathematical Sinica, Chinese Series, 2004, 47(6): 1099-1106. [6] XU Z T, XING H Y. Kamenev-type oscillation criteria for semilinear elliptic differential equation [J]. Northeast Math J, 2004, 20(2): 153-160. [7] ZHUANG R K, WANG Q R, ZHU S M. Domain oscillation criteria for second order nonlinear elliptic differential equations [J]. Acta Mathematical Sinica, Chinese Series, 2005, 48(3): 527- 534. [8] ZHUANG R K. Annulus oscillation criteria for second-order nonlinear elliptic differential equations [J]. J Comput Appl Math, 2008, 271(1): 268-276. [9] YANG Q. On the oscillation of certain nonlinear neutral partial differential equations [J]. Appl Math Lett, 2007, 20(8): 900-907. [10] PHILOS GH G. Oscillation theorems for linear differential equations of second order [J]. Arch Math, 1989, 53: 483-492. [11] KONG Q K. Interval criteria for oscillation of second order linear differential equations [J]. J Math Anal Appl, 1999, 229: 258-270.
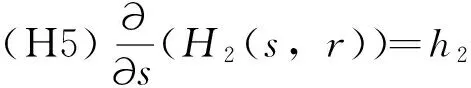
1 主要结果
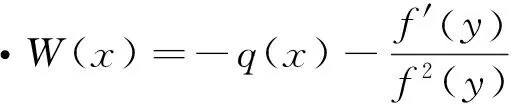
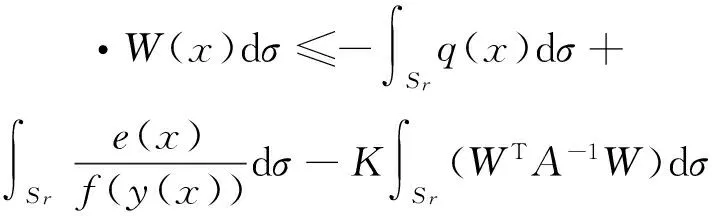
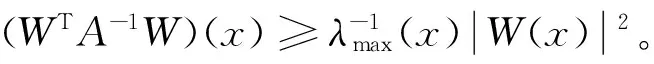
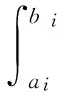
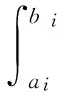
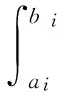
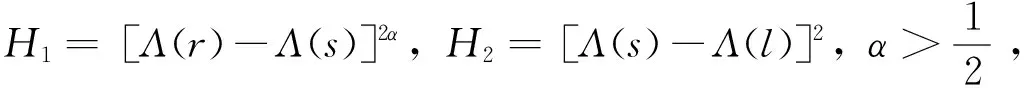
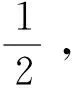

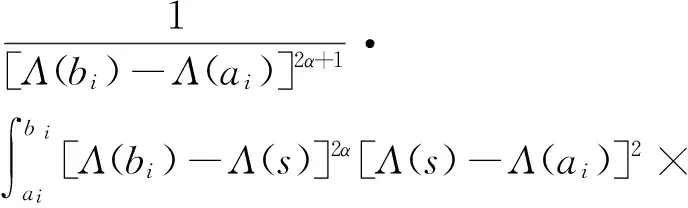
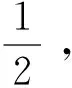
2 例子