多元位置3值连续相位调制解调方法
靳 一 吴乐南 何 峰 余 静
(东南大学信息科学与工程学院,江苏 南京 210096)
引 言
近年来,高速增长的宽带无线业务对无线通信提出了越来越高的要求,直接导致空中的无线电频谱资源愈加紧缺.如何在单位频带内高速传输信息,即提高频谱利用率,已成为新一代信息传输系统的核心竞争指标和关键性技术.鉴于此,一种称作超窄带(Ultra Narrow Band,UNB)调制的高频谱利用率技术受到关注.从其发明人H. R. Walker[1-2],到国内的郑国莘[3-4]、吴乐南[5]、周正[6]和王红星[7-8]等团队均对此展开了研究.其中,连续相位的扩展二元相移键控(Extend Binary Phase Shift Keying with Continuous Phase,CP-EBPSK)[5]、随机极性CP-EBPSK[9]和多元位置随机极性改进的CP-EBPSK(Modified CP-EBPSK,MCP-EBPSK)[10-11]等不对称连续调相技术,即使在严格的-60 dB(甚至更低的)功率带宽下,仍呈现出了较高的频谱利用率.具体在调制端,随机极性CP-EBPSK利用调相极性(即相位正负)的随机化大幅压低了CP-EBPSK功率谱中的离散线谱;而多元位置随机极性MCP-EBPSK又利用功率谱成型和多进制调制进一步提高了随机极性CP-EBPSK调制的频谱利用率.但在接收端,对于这些CP-EBPSK类型调制信号的冲击滤波输出响应,均首先采用包络检波消除信号调制相位的随机极性,再门限判决实现解调.虽然简单,却是一种非相干解调方式,理论上还非最佳.
本文着重从两方面继续改进,一方面,注意到上述相位调制中引入随机极性仅仅是为了消除功率谱中的线谱,正负相反的极性本身并未承载任何信息,如能有效利用,即可调制1位数据,同时也不致影响对于线谱的抑制,经过加扰的数据码流本身就是随机的.为此,引入3值调相取代上述的随机调相,先后提出了3值MCP-EBPSK调制和多元位置3值MCP-EBPSK调制,从而在相同的码元周期内每个符号可比随机极性调相多传输log23-log22≈0.58 bit数据,提高了信息传输速率和频谱利用率.
另一方面,为了分辨信号相位并进行理论上性能更好的相干解调,设计了基于反向传播(Back Propagation,BP)神经网络[12]和支持向量机(Support Vector Machine,SVM)[12-14]的非线性判决器,获得了更好的解调性能,从而提升了不对称连续调相通信系统的能量利用率.
1 多元位置3值MCP-EBPSK调制
1.1 3值MCP-EBPSK调制
3值的MCP-EBPSK调制在单个码元周期[0,NTc]内定义为:
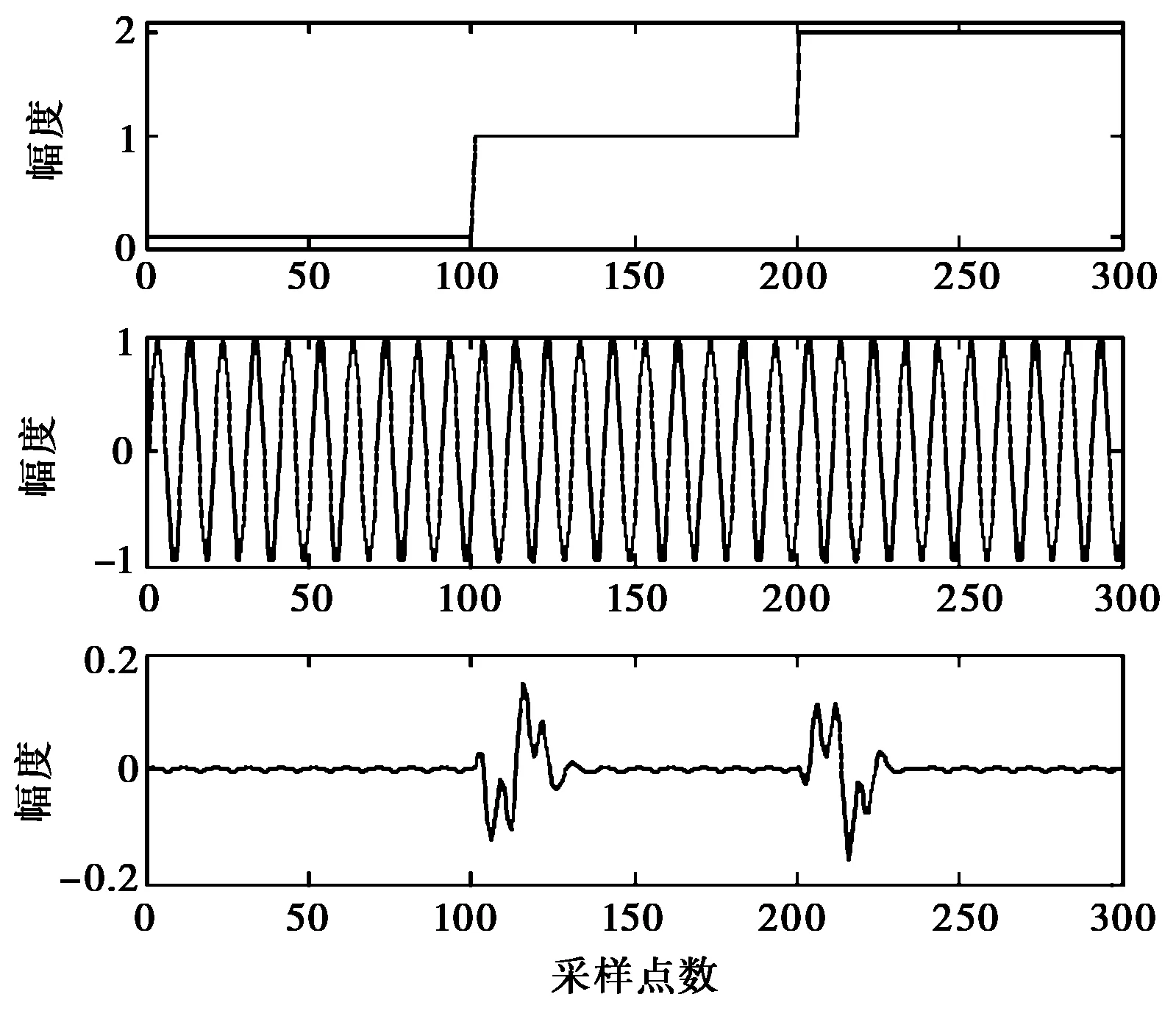
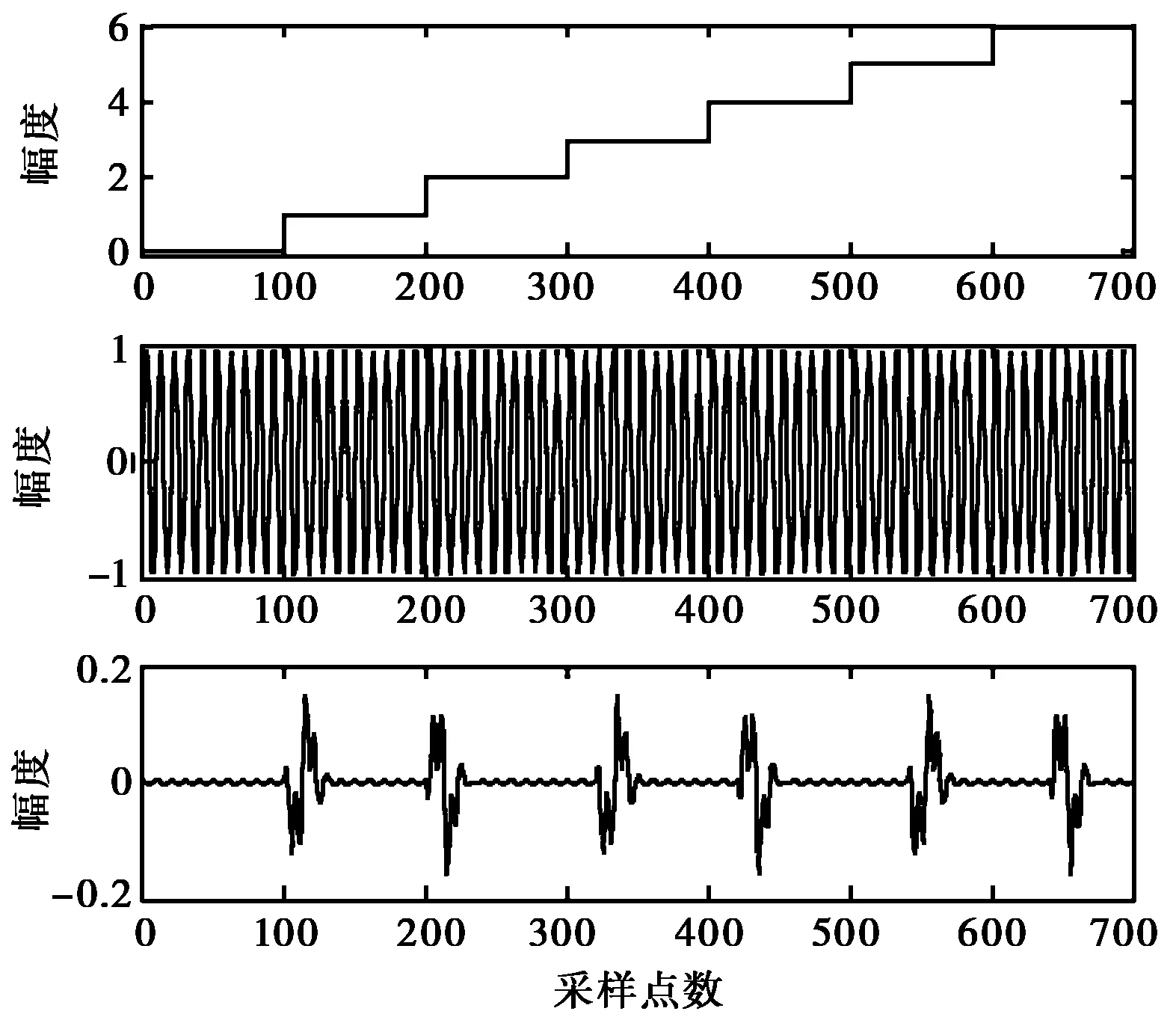
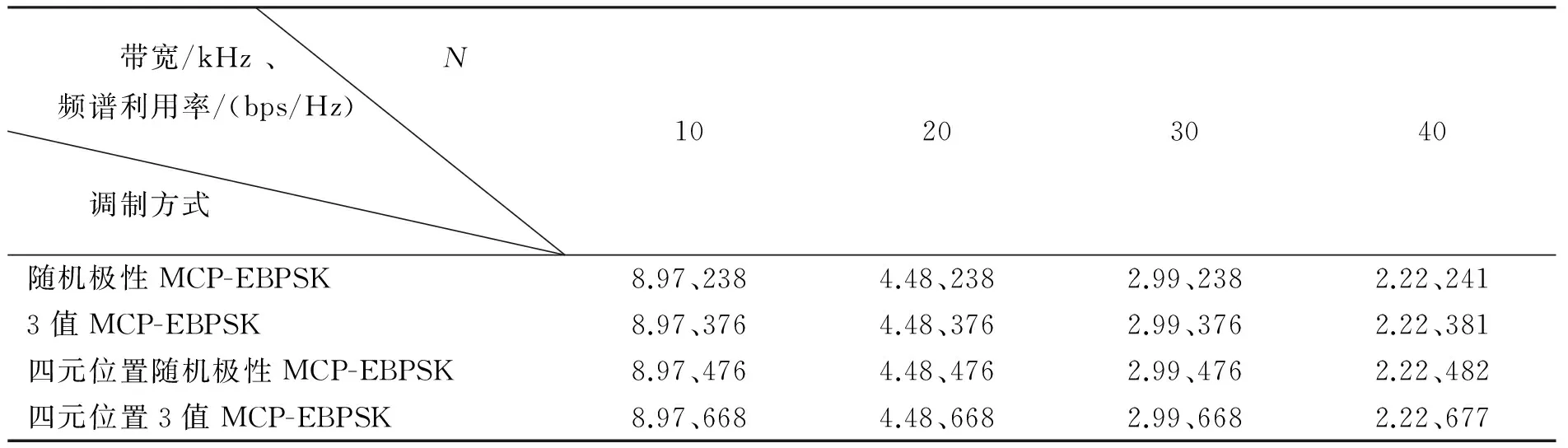
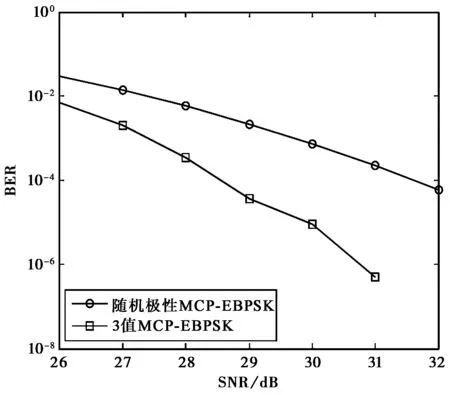
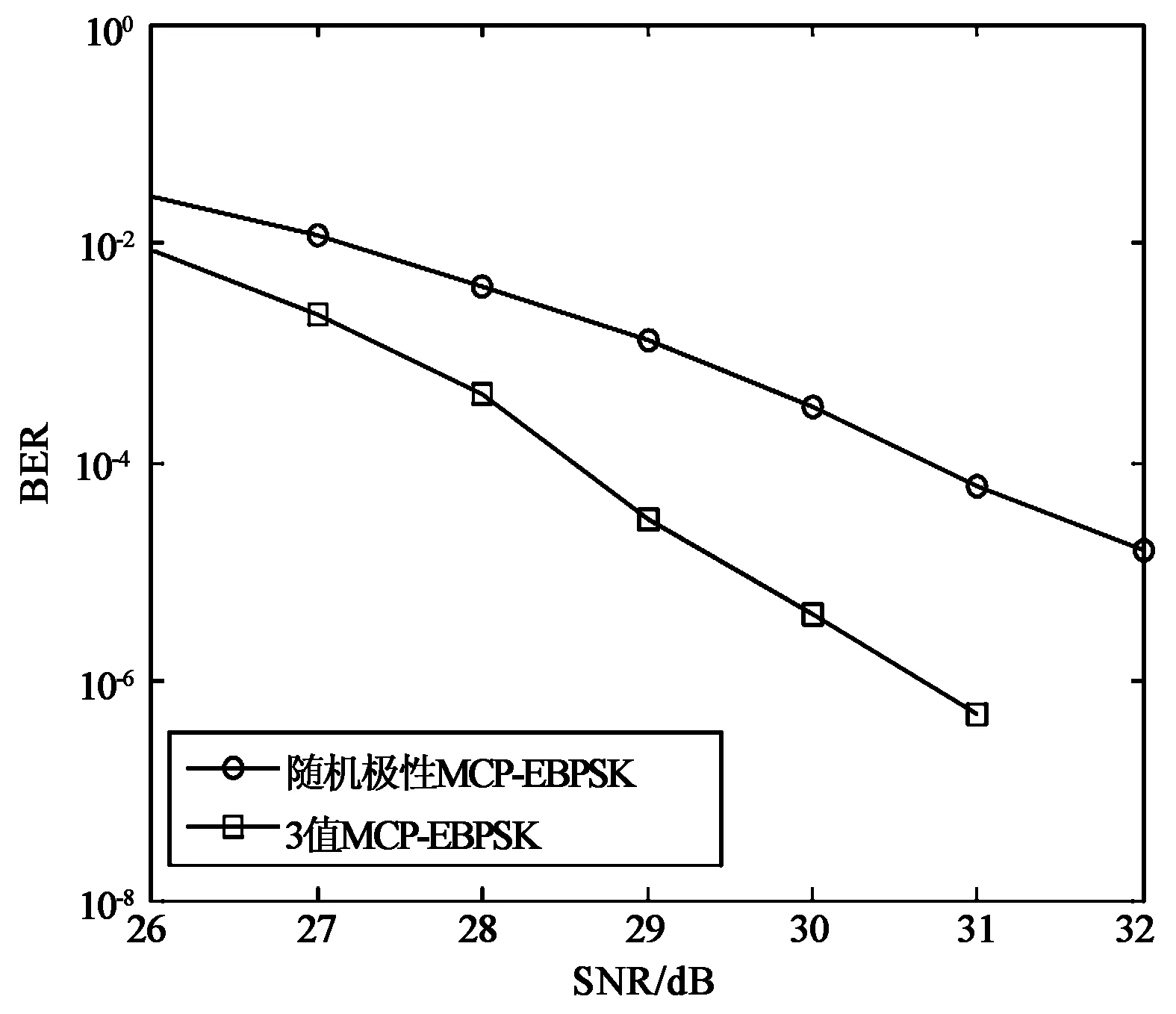
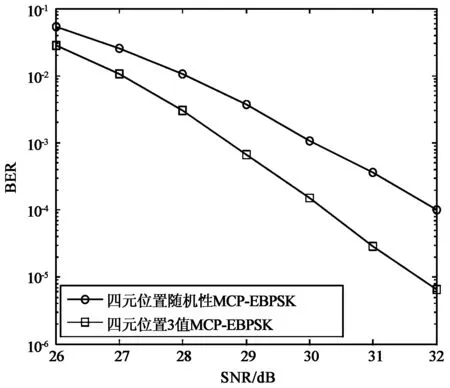
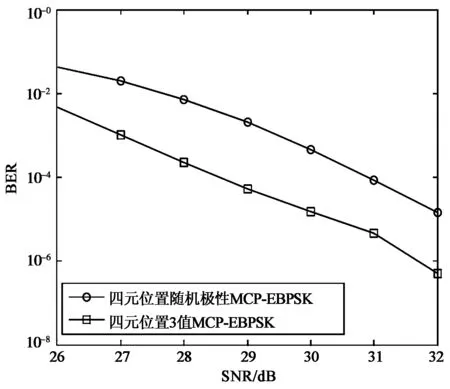
S0(t)=sinωct0≤t (1) (2) (3) 式中:S0(t)、S1(t)和S2(t)分别代表码元“0”、“1”和“2”的调制波形;ωc为调制载波的角频率;Tc=2π/ωc为载波周期,码元周期为N个载波周期; 码元“1”和“2”的调制时段为K个载波周期(N和K均为整数); 0<Δ<1为调相指数;η∈(0,1]为功率谱形状调节系数.当N=4,K=2,Δ=η=0.5时,可得如图1所示的调制信号波形. 图1 3值MCP-EBPSK调制信号 在式(1)~(3)所示的3值MCP-EBPSK调制的基础上,充分利用码元周期内的相位跳变位置和极性来进行二维调制,则扩展成了多元位置3值MCP-EBPSK调制,其表达式为: S0(t)=sinωct0≤t (4) S2k-1(t)= (5) (6) 式中: 1,2,…,2k-1,2k为非“0”信息序列码元(k=1,…,M-1,M为随机调相时的进制数);S0(t)是发送码元为“0”的调制波形;S2k-1(t)是发送码元为“2k-1”的调制波形;S2k(t)是发送码元为“2k”的调制波形; 0≤rg<1为符号保护间隔控制因子.由M、K、N、η、Δ和rg构成了改变信号带宽、传输效率和解调性能的一组“调制参数”.与多元位置随机极性MCP-EBPSK相比,多元位置3值MCP-EBPSK调制信号具有相同的功率谱结构,但因在单个码元周期内传输的非“0”码元符号数是原来的2倍,即如果前者为M进制,则后者为2(M-1)+1=2M-1进制,故后者比前者每符号可多传输log2(2M-1)-log2M=log2(2-1/M)位数据,当M较大时约为1 bit,使信息传输速率和频谱利用率都得以提高. 数字冲击滤波器[15]是由1对共轭零点和多对共轭极点构成的无限冲击响应(Infinite Impulse Response,IIR)滤波器,在其极窄的通带内可将3值MCP-EBPSK调制信号的微弱相位跳变转化为具有明显差异的幅度冲击,并在输出波形上体现调制波形的极性变化,有利于解调.该特殊滤波机理同样适用于多元位置3值MCP-EBPSK调制信号的解调,使得冲击输出波形在幅度、位置和波形上均存在显著差异,可据此设计基于BP神经网络和SVM多分类器的解调器,具体方法将在2.2节中给出.目前,数字冲击滤波器的设计方法有人工设计和优化算法自动搜索两种,文献[15-16]已进行了详细描述,不再赘述.本文选用的数字冲击滤波器具有1对共轭零点和3对共轭极点,其传输函数为 (7) 式中: b1=-1.618 495 523 346 314;b2=1; a1=-1.973 401 307 621 458; a2=1.707 892 238 042 286; a3=-0.700 903 759 306 155; a4=0.130 496 898 023 677; a5=-0.002 568 125 322 230; a6=0.000 019 814 679 492. 当载频fc=21.4 MHz,采样频率fs=10fc,N=10,K=2,Δ=0.1和η=1/2时,将3值MCP-EBPSK调制信号和四元位置3值MCP-EBPSK调制(即七进制)信号分别通过式(7)所示的数字冲击滤波器时,可得如图2(a)和(b)所示的冲击输出(从上到下依次为:信息序列,调制波形和冲击输出波形).从图2可看出:1)“0”码元和非“0”码元的冲击输出波形在幅度上差异明显;2)非“0”码元的冲击输出波形在时间位置上存在差异;3)奇数序号非“0”码元的冲击输出波形和偶数序号非“0”码元的冲击输出波形在幅度上正负极性颠倒(互为反相,例如图2(b)中的“1”和“2”码元,“3”和“4”码元). (a) 3值MCP-EBPSK调制信号冲击输出 (b) 四元位置3值MCP-EBSPK调制信号冲击输出图2 冲击输出波形对比 2.2.1 BP神经网络 BP神经网络[12]是一种最简单的神经网络,由输入层、隐含层和输出层3部分构成,被广泛的应用于函数逼近、模式识别和分类等领域.在此,仅阐述其作为多分类器的原理,具体步骤为: 1) 对样本集进行特征向量提取,划分训练集和测试集,并分别进行归一化处理; 2) 合理设计BP神经网络,其中输入层和输出层的神经元数分别由特征向量维数、类别数决定,隐含层神经元数可根据经验值设定; 3) 若训练样本的类别号为g,则对应的期望输出第g个神经元值为1,其余神经元值均为0,从而训练BP神经网络; 4) 依次输入测试样本,利用步骤3)得到的BP神经网络进行分类,若输出端的第m个神经元输出值最大,则类别号为m. 2.2.2 SVM SVM[12-14]是一种基于统计学习理论的模式识别工具,利用核函数法将低维空间的不可分数据映射到高维线性空间实现分类.经典的SVM二值分类算法[12]为: 1) 已知一组输入样本xi和对应的期望输出yi∈{+1,-1} (i=1,…,L); 2) 选择合适的核函数K(xi,x)=φ(xi)φ(x)及其参数; 基于以上的SVM二值分类,现有的SVM多分类器有直接法和间接法两种构造方法.直接法,即多类目标函数法,通过一次求解目标函数实现多类别分类,但计算量很大,仅适用于小数据样本.间接法通过组合多个二分类器构造多类分类,通常有one-against-one[14]和one-against-all两种形式.本文选用前者,其具体作法为: 1) 训练时,在任意两类样本间设计一个SVM二值模型,故有n个类别就需要设计n(n-1)/2个SVM二值模型; 2) 将测试样本分别经过所有的SVM模型,并选择得票最多的类别作为分类结果. 2.2.3 基于BP神经网络/SVM的解调器 根据2.1节所述的冲击滤波机理,若将单个码元周期内的冲击波形样本点幅值作为特征向量,则可设计一个BP神经网络或SVM多分类器来进行解调.多分类器需要经过训练才能使用,即优化分类器的参数(主要是结构和权系数).在此,就是让分类器“学习并记住”数字冲击滤波器对多元位置3值MCP-EBPSK调制信号的冲击波形在幅度、位置和相位极性上的差异,以期在真实环境中也能得到良好的分类性能,其模型如图3所示.可看出,该解调器的工作过程分为训练和测试两个阶段,具体如下: 1) 训练阶段 在一定信噪比下,随机选取固定数量的训练码元,并将调制后的多元位置3值MCP-EBPSK调制信号依次经过加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道和数字冲击滤波器.然后,将冲击滤波波形的归一化样本点幅值作为BP神经网络或SVM的输入向量,并针对训练码元序列设计合适的目标向量,从而训练BP神经网络或SVM. 2) 测试阶段 将测试码元的数字冲击滤波波形的归一化样本点幅值依次作为训练阶段所得BP神经网络或SVM的输入向量.然后,将BP神经网络或SVM的输出映射成码元,并和测试码元对比,进行误码率(Bit Error Rate,BER)统计.可看出,与文献[17]给出的基于BP神经网络和SVM的随机极性MCP-EBPSK解调器模型相比,图3所示的解调器无需对数字冲击输出波形进行包络检波,因为需要利用冲击波形的相位极性来实现解调,故在一定程度上减少了信息的损失. 图3 基于BP神经网络或SVM的解调器 保持仿真参数与2.1节一致,采用基于Hamming窗的Welch谱估计法对随机极性MCP-EBPSK和3值MCP-EBPSK调制信号进行功率谱估计.为保证谱估计的精度,仿真采用10万个码元和226点快速傅里叶变换(Fast Fourier Transform,FFT),得到了图4(a)和(b)所示的仿真结果.可以看出,两种调制方式的功率谱结构和形状几乎是相同的.同时,在同样的仿真条件下,对四元位置随机极性MCP-EBPSK和四元位置3值MCP-EBPSK调制信号进行了功率谱估计,得到了如图4(c)和(d)所示的仿真结果.可以看出,两种调制方式的功率谱结构和形状也几乎是相同的.为了进一步对比四种调制方式的功率谱特性,按照美国联邦通信委员会(Federal Communication Commission,FCC)严格的-60 dB(即信号的功率谱幅值为载频处功率谱幅值的10-6)带宽标准,统计了其-60 dB带宽和频谱利用率指标,得到了如表1所示的结果.可以看出:1) 四种调制方式的功率谱高度集中在载频附近,载频处幅度高于其它边带约70 dB(1千万倍),造成了其-60 dB带宽是单根谱线的“假象”;2) 四种调制方式的-60 dB带宽是相同的,但因不同调制方式在单个码元周期内传输的比特数不同(具体为,随机极性MCP-EBPSK在单个码元周期内传输比特数为1,3值MCP-EBPSK在单个码元周期内传输比特数为log2(3)≈1.58,四元位置随机极性MCP-EBPSK在单个码元周期内传输比特数为log2(4)=2,四元位置的3值MCP-EBPSK在单个码元周期内传输的比特数为log2(7)≈2.81),故频谱利用率也呈现同样的倍数关系. (a) 随机极性MCP-EBPSK (b) 3值MCP-EBPSK (c) 四元位置随机极性MCP-EBPSK (d) 四元位置3值MCP-EBPSK图4 功率谱对比 带宽/kHz、 N 频谱利用率/(bps/Hz)调制方式10203040随机极性MCP-EBPSK8.97、2384.48、2382.99、2382.22、2413值MCP-EBPSK8.97、3764.48、3762.99、3762.22、381四元位置随机极性MCP-EBPSK8.97、4764.48、4762.99、4762.22、482四元位置3值MCP-EBPSK8.97、6684.48、6682.99、6682.22、677 在此,依旧保持调制参数不变,采用1 000万个码元对随机极性MCP-EBPSK调制、3值MCP-EBPSK调制信号进行解调性能仿真,解调器分别为文献[17]和图3所示的BP神经网络/SVM模型.在训练信噪比为29 dB,测试信噪比为26~32 dB(该范围根据文献[17]来确定,若取值很小,则几乎不能解调成功)时,采用1 000个训练码元的情况下,分别利用BP神经网络和SVM进行解调,得到了如图5(a)和(b)所示的BER曲线(其中,BP神经网络的隐含层神经元数为5,SVM的核函数为径向基函数).可以看出:1) 当采用BP神经网络解调,在BER为10-4时,3值MCP-EBPSK获得约3 dB信噪比提升;2)当采用SVM解调,在BER为10-4时,3值MCP-EBPSK获得约2 dB信噪比提升.同时,在相同的仿真条件下,对四元位置随机极性MCP-EBPSK调制、四元位置的3值MCP-EBPSK调制进行解调性能仿真,得到了如图5(c)和(d)所示的BER曲线.可以看出:1)当采用BP神经网络解调,在BER为10-4时,四元位置的3值MCP-EBPSK获得约2 dB信噪比提升;2)当采用SVM解调,在BER为10-4时,四元位置的3值MCP-EBPSK获得约2.5 dB信噪比提升.这是由于在随机极性MCP-EBPSK和四元位置的随机极性MCP-EBPSK解调时,对冲击滤波输出波形进行了包络检波,损失了相位信息. (a) 基于BP神经网络的解调性能 (b) 基于SVM的解调性能 (c) 基于BP神经网络的解调性能 (d) 基于SVM的解调性能图5 误码率对比 与多元位置随机极性MCP-EBPSK相比,本文提出的多元位置3值MCP-EBPSK调制可获得更高的信息传输速率和频谱利用率,且在BER为10-4时获得约2 dB的信噪比性能改善(若以Eb/N0来度量,改善还要更大些,因为比特率提高了).然而,多元位置的3值MCP-EBPSK的解调性能距离无线应用尚有较大差距,这一方面可引入信道编码及多天线系统来进一步改善其传输性能,而另一方面可首先考虑有线信道增容,因为我国有关标准(GB6510-86:30 MHz~1 GHz声音和电视信号电缆分配系统;GY/T 106-1999:有线电视广播系统技术规范)规定:有线电视系统的载噪比≥43 dB. [1] WALKER H R. VPSK and VMSK modulation transmit digital audio and video at 15 bits/sec/Hz[J]. IEEE Transactions on Broadcast Engineering, 1997, 43(1): 96-103. [2] WALKER H R. Ultra Narrow Band Modulation Textbook[M/OL].[2012-08-10],http://www.vmsk.org/. [3] ZHENG Guoxin, FENG Jinzhen, JIA Minghua. Very minimum chirp keying as a novel ultra narrow band communication scheme[C]// Proceedings of Sixth International Conference on Information, Communications and Signal Processing. Singapore, December 11-13, 2007: 1-3. [4] ZHENG Guoxin, YANG Weiying. The orthogonal very minimum chirp keying (OVMCK) modulations with very high bandwidth efficiency[C]// IEEE International Symposium on Antenna and Propagation and USNC/URSI National Radio Science Meeting. San Diego, July 5-11, 2008: 3182-3185. [5] WU Lenan, FENG Man, QI Chenhao, et al. Recent patents on ultra narrow band modulations[J]. Recent Patents on Signal Processing, 2011, 1(1): 36-47. [6] LI Bin, ZHOU Zheng, ZOU Weixia. RPPK modulation with high data rates[J]. Science China: Information Sciences, 2010, 53(2): 344-354. [7] 王红星, 王洪利, 毛忠阳, 等. 基于循环谱特性的扩展二元相移键控解调算法[J]. 电波科学学报, 2010, 25(5): 935-939. WANG Hongxing, WANG Hongli, MAO Zhongyang, et al. The demodulation algorithm for EBPSK based on cyclic spectrum characteristic[J].Chinese Journal of Radio Science, 2010, 25(5): 935-939. (in Chinese) [8] 王红星, 王洪利, 张 磊, 等. EBPSK及其优化调制信号的二阶循环平稳特性分析[J]. 电波科学学报, 2010, 25(1): 42-46. WANG Hongxing, WANG Hongli, ZHANG Lei, et al. Cyclostationarity analysis on EBPSK and its optimization[J]. Chinese Journal of Radio Science, 2010, 25(1): 42-46. (in Chinese) [9] 张 宇, 应鹏魁, 吴乐南. 伪随机调制的CP-EBPSK通信系统[J]. 东南大学学报: 自然科学版, 2012, 42(2): 209-213. ZHANG Yu, YING Pengkui, WU Lenan. Pseudo-random modulated CP-EBPSK communication system[J]. Journal of Southeast University: Natural Science Edition, 2012, 42(2):209-213.(in Chinese) [10] 靳 一, 吴乐南, 冯 熳, 等.一种随机极性MCP-EBPSK调制解调器[J]. 电子与信息学报, 2012,34(7): 1647-1652. JIN Yi, WU Lenan, FENG Man, et al. An MCP-EBPSK modem with random-polar[J]. Journal of Electronics & Information Technology, 2012, 34(7): 1647-1652. (in Chinese) [11] 靳 一, 吴乐南, 冯 熳, 等.一种多元位置随机极性连续相位调制解调器[J]. 电波科学学报, 2012, 27(5): 931-936. JIN Yi, WU Lenan, FENG Man, et al. An M-ary and continuous phase modem with random-polar[J]. Chinese Journal of Radio Science, 2012, 27(5): 931-936. (in Chinese) [12] 高 隽. 人工神经网络原理及仿真实例[M]. 北京: 机械工业出版社, 2007. [13] LIN Kengpei, CHEN Mingsyan. On the design and analysis of the privacy-preserving SVM classifier[J]. IEEE Transactions on Knowledge and Data Engineering, 2011, 23(11): 1704-1716. [14] ANGULO C, GONZALEZ L. 1-v-1 Tri-class SV Machine[C]// Proceedings of the 11th European Symposium on Artificial Neural Networks. Bruges, April, 2003: 355-360. [15] 冯 熳, 高 鹏, 吴乐南. 超窄带调制信号的特殊滤波分析与仿真[J]. 东南大学学报: 自然科学版, 2010, 40(2): 227-230. FENG Man, GAO Peng, WU Lenan. Analysis and simulation of special filtering based on ultra narrow band modulated signal[J]. Journal of Southeast University: Natural Science Edition, 2010, 40(2): 227-230. (in Chinese) [16] 余 静, 吴乐南, 靳 一. 基于量子粒子群优化的数字冲击滤波器自动设计[J]. 东南大学学报:自然科学版,2012, 42(2):224-228. YU Jing, WU Lenan, JIN Yi. QPSO-based on auto-design of digital Impacting filters[J]. Journal of Southeast University: Natural Science Edition, 2012, 42(2):224-228.(in Chinese) [17] 靳 一, 吴乐南, 冯 熳, 等. 随机极性MCP-EBPSK传输性能[J]. 东南大学学报: 自然科学版, 2012, 42(6): 1031-1035. JIN Yi, WU Lenan, FENG Man, et al. Transmission Performance of MCP-EBPSK with Random Polar[J]. Journal of Southeast University: Natural Science Edition, 2012, 42(6): 1031-1035. (in Chinese)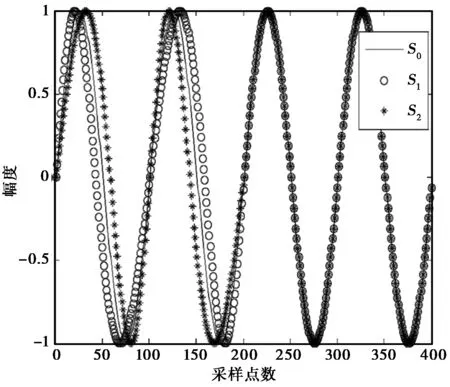
1.2 多元位置3值MCP-EBPSK调制
2 解调器
2.1 冲击滤波原理
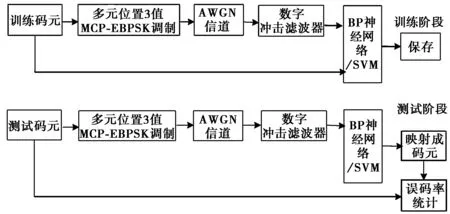
2.2 解调器模型
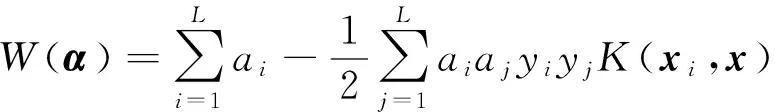
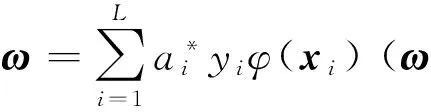
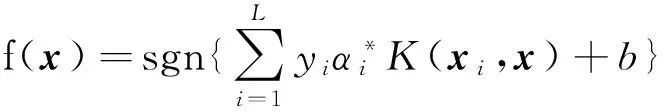
3 仿 真
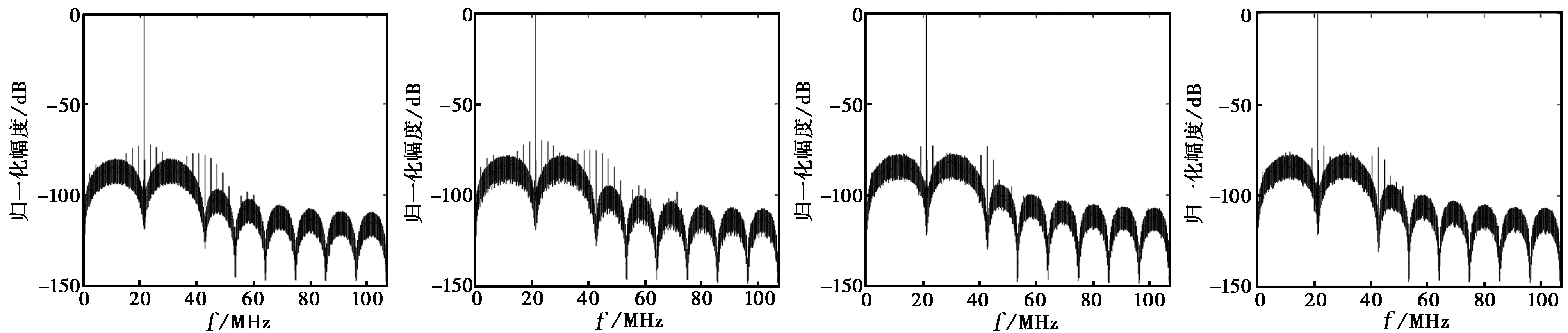
3.1 功率谱特性
3.2 解调性能
4 结 论

