试论独占加共享的频谱划分模式

吴乐南

(东南大学信息科学与工程学院，江苏 南京 210096)

引 言

目前普遍采用的频谱管理模式可追朔到20世纪初，当时认为频谱是有限的自然资源，为了避免相互干扰，必须通过政府行为将其划分成很多小频段分配给不同需求的用户独占. 香农、Nyquist按照理想矩形带宽所导出的信道容量和2 Baud/Hz的单位频谱利用率理论极限，即与这种矩形频谱划分相适应. 随着频谱资源的日益紧缺，矩形独占式频谱划分的低效备受关注.美国奥巴马指出目前这种频谱短缺现状已严重影响到美国国家技术创新能力的发挥，并在2010年6月特别签署了名为“发动无线宽带革命”的总统备忘录，督促尽快制订开放500 MHz频谱给无线宽带业务的时间表[1]. 许多西方发达国家如英国等，也都采取积极措施，开放频谱，促进创新. 我国也有相应举措.

而提高信息传输体制本身的频谱利用率和能量利用率，应该是解决频谱短缺和电磁污染的治本之策. 但是，丰富人类认知需完备基础理论体系，创立全新体制需突破传统理论框架，发展绿色通信需提升基本物理层性能，规划频谱改革需应对技术创新挑战. 为此本文将针对超窄带(Ultra Narrow Band, UNB)调制类似正弦波的信号特征以及我们的研究进展，提出超窄“频谱树”独占加较宽“频谱草”共享的非矩形频谱划分模式，归纳值得探索的研究方向，为解决频谱需求提供理论和技术思路.

1 现行矩形频谱划分的局限性

1.1 与工程现实不一致

由于矩形频响的理想滤波器不可实现，故邻带间干扰总是存在，只是根据频带划分必须低于一定门限，因而理论上的矩形频谱划分与实际上的工程带宽定义并不一致[2].传统的用户独占频谱管理模式，某种意义上也是一种频谱共享方式，只不过对不同用户带内外辐射功率有不同要求.

1.2 难以容纳新体制

根据由理想矩形带宽导出的经典信道容量

C=Blog2(1+SNR),

(1)

能量效率的极限(带宽B趋于无穷大)启示了时域的冲激函数波形和频域的白噪声功率谱，奠定了脉冲超宽带(Impulse Radio-Ultra Wide Band, IR-UWB)技术的理论框架；而频谱效率的极限(带宽B趋于零)则启示了时域的正弦波形和频域的冲激线谱，理应对偶地建立所需信噪比(Signal to Noise Ratio, SNR)无穷大的超窄带技术的理论框架，无奈纯正弦波不携信息，而对正弦载波的任何微小数字调制，理论上都会使其频谱无穷展宽. 因而，欲容纳“类正弦”调制信号和阐释UNB通信系统，必须拓展经典的香农信道容量框架[3].

1.3 “封顶”技术进步

虽说用正弦信号承载信息几乎是近百年来通信系统的固有模式，但实际上相移键控(Phase Shift Keying, PSK)等常用调制信号由于抑制了载波，在频域已失去了正弦函数的基本特征，即载频处的冲激函数.因而经典的匹配滤波理论和传统的相关检测方法并不能合理阐释连同载波一起传输的类正弦通信体制的优异性能[4-7]，而实际系统的发射功率也不足以支撑多电平正交调幅(Multiple Quadrature Amplitude Modulation, M-QAM)、多进制调相(Multiple PSK, M-PSK)等多进制调制单纯以增加信号星座点数来提高频谱效率.因此，在经典信息论框架内，“高速”必须“宽带”，而通信效率的提高，也只能朝着式(1)的香农限不断“逼近”，包括引入多天线(Multi-Input Multi-Output, MIMO)等技术后的新极限.

1.4 导致资源浪费

传统的管理体制沿用独占式频谱分配策略将资源分配给固定的授权用户，在某种程度上导致了有限的频谱资源与高增长的频谱需求的矛盾. 对此虽然认知无线电(Cognitive Radio, CR)技术[8]着眼于从时间、空间和频率等多维度重复利用和共享频谱资源，将“频谱空穴”尽可能填满，有助于从顶层用好公共资源，但对物理层传输效率的提升即从底层减少频谱资源的占用，却无实质性改善.另外，针对非正弦信号的最佳接收机，用于解调类正弦的UNB调制信号也非最佳(详见2.2节).

2 类正弦体制的高效性

2.1 频谱利用率高效

我们曾指出，为了实现通过率带宽意义上的超窄带高效传输，必须在发射信号中保留一个正弦载波，并充分利用正弦载波的能量携带信息和提升解调性能[2]. 为此本节仅以一类扩展的二元相移键控(Extended Binary Phase Shift Keying, EBPSK)调制[2]为例，其简化表达式为

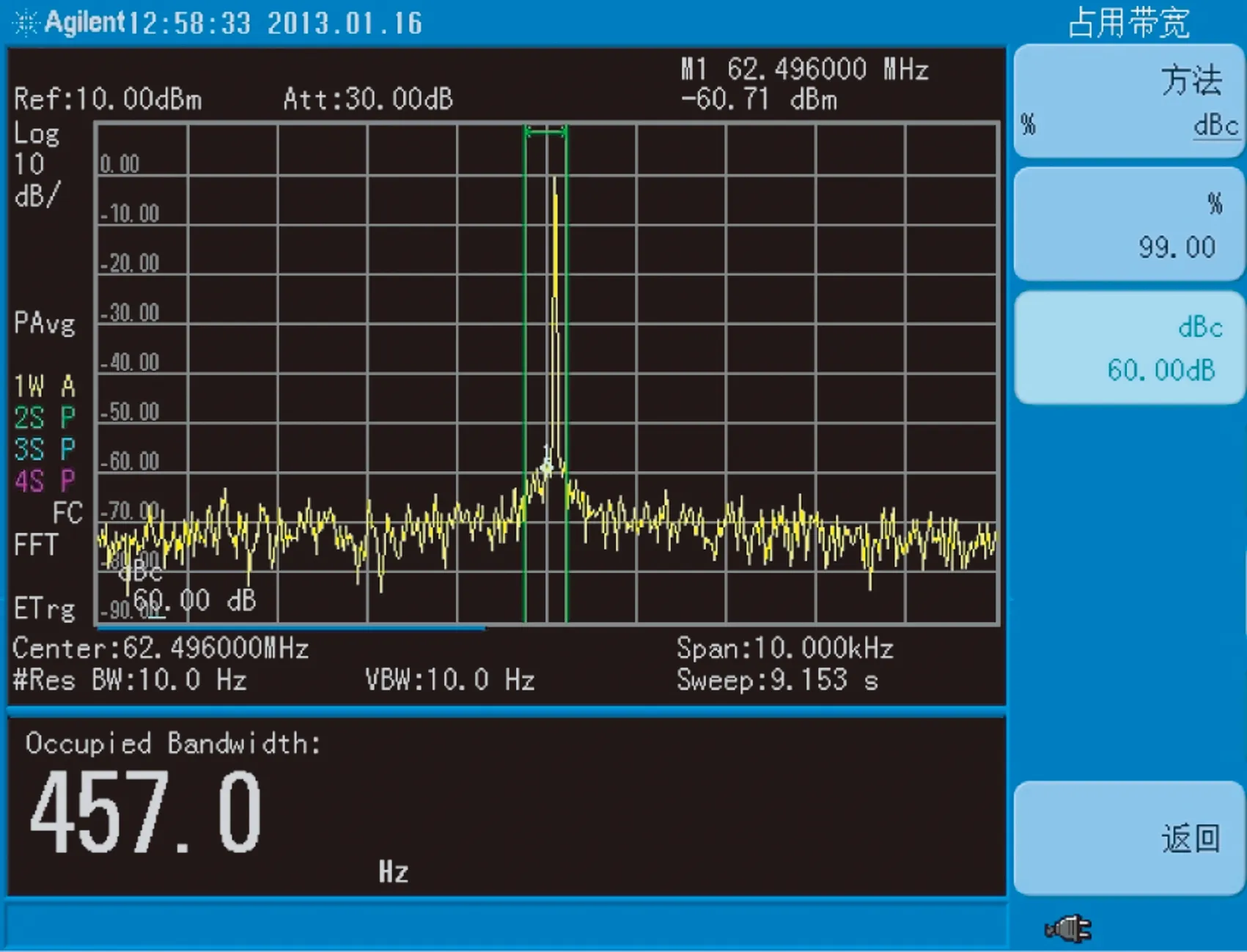
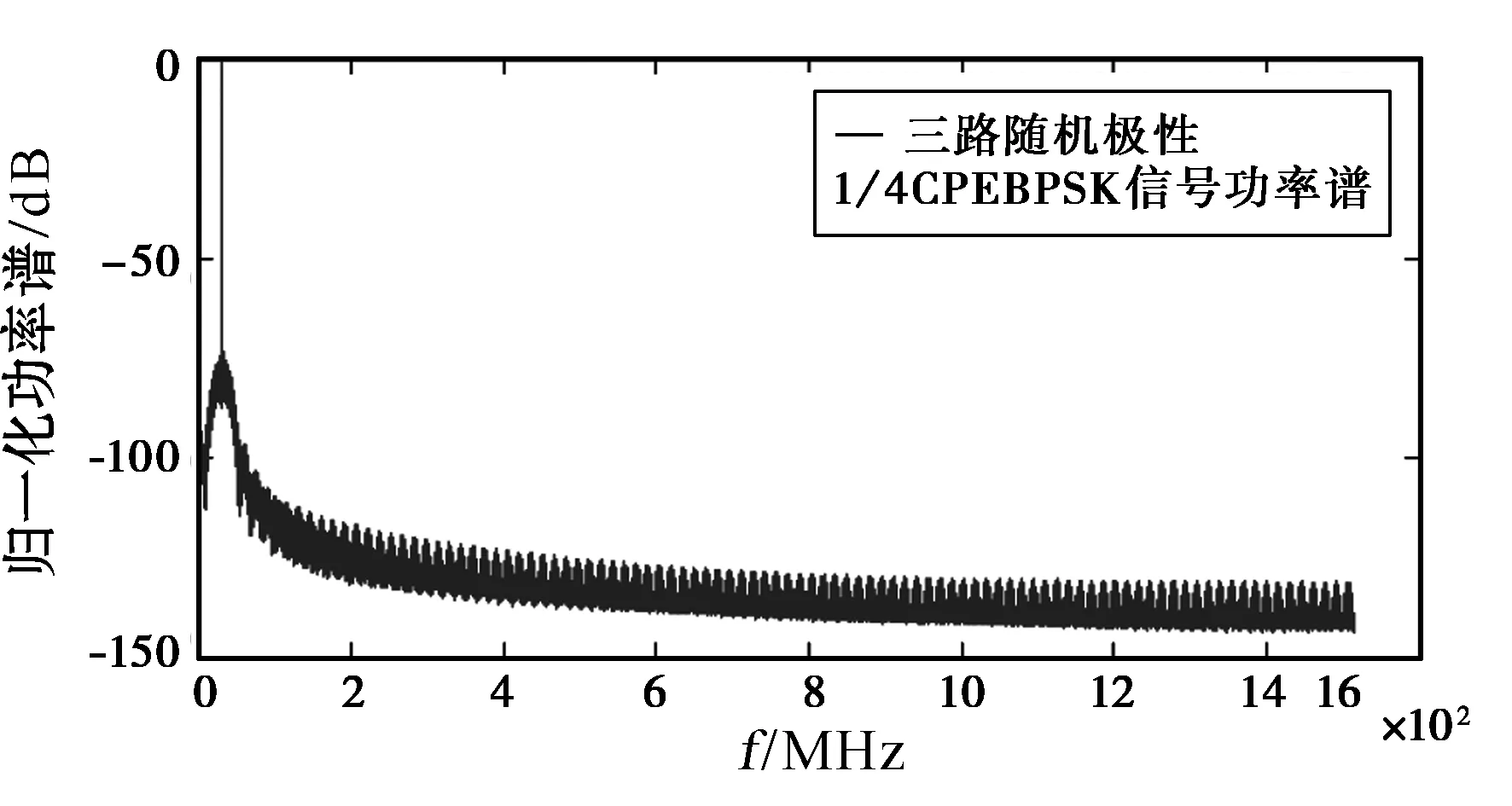
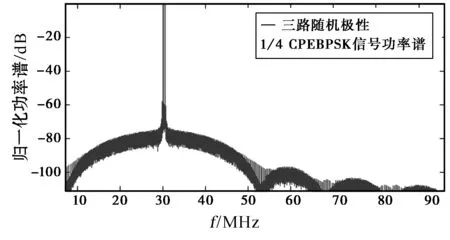
式中，s0(t)和s1(t)分别表示数据0和1的调制波形.在码元周期T(包含N个载波周期)内的键控调制时段τ

由于式(2)是0-1不对称的调制，于是可望在通过率带宽的意义上提高频谱利用率.式(2)又有以下3种更简单的特例.

1) 令B=A，得到反相调制(Phase Reversal Modulation, PRM)：

2) 令B=0，得到缺周期调制(Missing Cycle Modulation, MCM)：

3) 令A=0，得到窄脉冲调制，类似于传统的雷达脉冲：

由式(3)～(5)所表示的3种EBPSK调制的简单特例，具有熟知的(sincx)2功率谱包络，差别只是载波分量不同[9]. 极限情况取K=1甚至K=1/2，于是B=0而N足够大趋于UNB，而A=0则趋于IR-UWB. 表1给出缺周期调制在载频fc=2.4 GHz、N=1 200且发端未加任何成形滤波器时的仿真结果，此时传输码率为fc/N=2 Mbps. 可见，如果按照通过率带宽(即99%功率带宽)考核，此时3种K值的频谱利用率均超过1 500 bps/Hz；而当K=2时，即使按照严格的-60 dB功率带宽计算，也能达到bps/Hz>90的频谱利用率，且此时解调所需SNR<7 dB(详见2.2节).

表1 缺周期调制的效率

2.2 能量利用率高效

虽然类正弦调制通过极小化0-1波形差异得到了很高的频谱利用率，但若按照传统的相关检测思路去与0-1波形负相关的BPSK信号最佳接收机相比，当然不占优势[10-11]，必须充分利用正弦载波的能量提升解调性能.对此可指出如下事实：

1) 尽管经典匹配滤波器作为白噪声干扰下确知信号波形输出SNR最大的线性滤波器，对于正弦信号仍然适用，但那只是在一个(或有限的)码元周期T内.

2) 不对称的二进制调制为相邻码元提供了内在的保护间隔T-τ，有利于对接收信号进行多码元跨周期积累.

3) 常用的锁相环可匹配滤波正弦信号，但非线性环节引入了门限效应，而从各种基本的正弦振荡器、传统的高灵敏度超再生接收机，到近期的随机共振[12]和Duffing振子[13]，均表明谐振能更加快速有效地积累正弦能量.

4) 电容上电压不能突变，电感中电流不能突变，那么在谐振于EBPSK载频的窄带LC回路中，能量不能突变. 因此，对于“0”和“1”等概率的PRM或MCM信号，谐振回路平均有(2T-τ)/2T的时间是吸取、放大和存储载波能量，仅在码元“1”的键控调制起始处，要动用自己的储能来阻止输入信号载波相位或幅度的突变，从而产生输出电平反弹，波形幅度显著变化.τ时段后又继续“充电”，并周而复始. 且正弦载波是功率型信号，理论上能量无穷大，足以支撑回路储能；而理论上白噪声是连续谱，没有代表点频简谐振荡的离散线谱，即使在谐振点也难有大提升.

基于这些事实和分析，采用无限冲激响应(Infinite Impulse Response, IIR)结构，实现了一种特殊的单零点-多极点数字带通滤波器[14]，可在SNR<0时以幅度过冲突显出调制信息，故称数字冲击滤波器. 对于表1参数的MCM信号添加高斯白噪声(Additive White Gaussian Noise, AWGN)后，对冲击滤波响应的包络进行局部积分再门限判决，不加任何信道编码，并取误比特率BER=10-5时的信噪比计入表1(K=1和2时冲击滤波器取2对共轭极点，K=4时取4对共轭极点)，可见在如此高的频谱利用率下仍有不错的解调性能.

按照经典通信理论，正弦载波不含信息、白白浪费功率且可在接收端恢复，因而，现有系统几乎都抑制发射载波，难以解释表1中保留极强载波的MCM信号的优良解调性能. 其实，这就是利用载波能量提升解调性能的一种方式. 已经发现在AWGN信道当fc=10 MHz、K∶N=2∶20、BER=10-3并采用单零点-3极点冲击滤波器辅助解调时，MCM/PRM信号相对于式(5)的窄脉冲调制表现出了14 dB的“载波辅助增益”[9]. 采用人工神经网络判决取代幅度判决也证实了这一现象.

数字冲击滤波器的设计思路也可推广到模拟冲击滤波器[15]. 实测一个中心频率为62.5 MHz的晶体冲击滤波器，其-1.5 dB、-3 dB、-6 dB和-40 dB带宽分别只有0.50、1.06、2.25和5.88 kHz，而码率高达1.249 6 Mbps的PRM信号(周期调制，占空比约20%)却能顺利通过带宽如此窄的晶体滤波电路并在信息调制处产生陡峭的幅度冲击(图1).这一性能非现有物理层技术可比拟，更非经典滤波理念[16]、香农极限和最佳接收理论可解释，且这样的高能效还可望在表1所示的超高频谱利用率下同时达到.

图1 实测62.5 MHz晶体冲击滤波器对1.249 6 Mbps码率PRM信号(下)的冲击输出(上)

诚然，表1仿真时发端未进行任何限带. 而在同等的20 MHz带宽限制和BER=10-6时，经典的伪码扩频BPSK调制系统2 Mbps码率时SNR≈1.6 dB，而PRM系统3.5 Mbps码率时SNR≈0 dB，表明EBPSK系统提供了比伪码扩频BPSK系统更大的容量[17]. 而如果利用模拟的晶体冲击滤波器，则由于噪声带宽缩窄，接收机灵敏度更可望大幅提高.

3 独占加共享频谱划分模式的技术合理性

3.1 充分而灵活地利用现有频谱资源

图2是62.5 MHz的PRM发射功率谱实测，调制占空比K∶N=3∶1 600，码率53.5 kbps，其-60 dB功率带宽只有457 Hz. 可见，类似正弦波的UNB调制信号功率谱同时具有覆盖式和衬垫式频谱共享的特点，只是其“频谱树”带宽更窄，几乎就是载波的正弦信号频谱；而“频谱草”也可比UWB功率谱密度更低，直至淹没在背景噪声下. 独占加共享的频谱划分模式相当于在背景噪声下又开发出一层频谱资源，因其与正弦载波严格相关，故这一层类噪声频谱能被有效利用.若借此推进对于传统管理模式的改革，解决与现有无线系统的共存和电磁兼容，则可望将频谱利用率大幅提高.

图2 PRM信号发射功率谱实测

另一方面，如果允许独占加共享的频谱划分模式，就可将UNB调制信号中低而宽的“频谱草”保留到解调时提高处理增益. 模拟通信系统中解调器输出信噪比与输入信噪比的比值，叫做调制制度增益，或信噪比增益，而冲击滤波器将原先在时域不易察觉的相位调制转化或突出为更加明显的调幅-调相，放大了数据“0”和“1”的波形差异，有利于解调判决，在一定程度上得到了系统模拟部分的调制制度增益.

3.2 合理而自然地容纳密集多载波体制

尽管按照无线电管理部门现有的带宽定义，UNB体制都不难适应目前的频谱管理模式，但为了“旧瓶装新酒”而削足适履，显然不会是、也不应是一种最佳解决方案. 而在独占加共享的频谱划分模式下，以超窄“频谱树”为特征的不同频率单载波信道就可以“大胆”靠近和大部分重叠而形成更加密集的多载波传输体制，传输码率和频谱利用率可望显著提高，而能效也可利用冲击滤波器组来极大提升. 如果说，现有调制技术已将多根“铜线”捆绑成“电缆”，即将一系列窄带信道正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)成一个宽带系统，则UNB体制试图将铜线提速为“光纤”. 而欲将bps/Hz/SNR综合效率已超过现有“铜线”的“光纤”，再“高密度”地捆绑成容量巨大的无线“光缆”，就必须突破现行的矩形频谱划分模式.在此“高密度”意指UNB调制的各子载波不必拘泥于传统OFDM体制的正交性限制(理论上应只取决于接收机锁相环分辨力)，更无需连续地依序配置，完全可以见缝插针地随时置于任何“认知”到的频谱缝隙和频谱“破碎带”. 图3即为3路二进制随机极性MCP-EBPSK调制[18]的混叠功率谱，载频分别为30 MHz、30.3 MHz和30.6 MHz(为便于观看和仿真没有更靠近)，每路码率约300 kbps，且均能正常解调.

由于单载波的UNB调制本身码率高有利于时分；图1的PRM冲击滤波输出便于码分或进一步提高弱链路解调性能；图3的密集多载波模式便于频分；同时，该体制并不妨碍引入MIMO技术提升系统性能和实现空分. 因此，密集多载波体制有利于建立时-频-码-空多维复用宽带无线传输的理论框架和多维联合优化设计方法.

(a) 全局图

(b) 展宽图图3 3路随机极性MCP-EBPSK调制的混叠功率谱

4 亟待必要的理论支撑

通信史上，人为的矩形频谱划分实施约40年后才有了相应的香农信道容量，但该容量沿袭60余年后已无法包容和解释许多高效的类正弦体制. 而UNB是技术突破在先，理论解释滞后，故为了探索超窄“频谱树”独占加较宽“频谱草”共享的非矩形频谱划分模式，有必要平行地导出与之相应的非香农信道容量和单位频谱利用率极限，而并非简单地“修补”经典香农公式对于UNB体制的解释，这是信息科学和通信技术发展中亟待解决的关键科学问题，有助于信息理论的丰富与完备，可望引发新的无线电技术革命.其科学意义似可用非欧几何相对于欧氏几何来比拟.

欲导出严格的信道容量闭合表达式需要付出非常艰苦的努力，但先从某些合理近似开始仍有望取得有价值的进展. 从图3可见，由于“频谱树”极细、“频谱草”很低，邻道干扰大为降低，因而有理由推断按照所提频谱划分方法得到的信道容量将大于按照传统矩形或带状频谱划分所导出的香农信道容量. 直观上，在摩天高楼林立地区，若将全部地下面积和空间甚至裙楼都作为共用(停车场、商店等)，显然有更大的空间容量.

5 结 论

1) 主要适应原始无线电技术发展水平的传统矩形频谱划分，当今已非唯一且未必最佳.

2) 类正弦体制因保留强载波并利用冲击滤波器谐振多码元能量，同时呈现出了极高频谱利用率和较高能量利用率.

3) 为匹配类正弦信号的功率谱特征，提出了超窄“频谱树”独占加较宽“频谱草”共享的非矩形频谱划分模式，可充分而灵活地利用现有频谱资源，合理而自然地容纳密集多载波体制.

4) 欲突破现有矩形频谱划分模式，亟待平行地导出非矩形频谱划分模式下的信道容量表达式和单位频谱利用率极限，为频谱分配改革和通信体制创新奠定理论基础.

本文只是初步论证了独占加共享频谱划分模式的技术合理性，具体划分方法有待深究.

致谢本文的主要思路得益于和北京邮电大学周正教授的讨论，博士生陈志敏、硕士生王继武和但洁斌进行了仿真和测试，特此致谢！

[1] LOCKE G, STRICKLING L E. Plan and Timetable to Make Available 500 Megahertz of Spectrum for Wireless Broadband[R]. U.S. Department of Commerce, 2010.

[2] 吴乐南. 超窄带高速通信进展[J]. 自然科学进展, 2007, 17(11): 1467-1473.

WU Lenan. Advances in UNB high data-rate communications[J]. Advances in Nature Science, 2007, 17(11): 1467-1473.(in Chinese)

[3] FENG Man, WU Lenan. Special non-linear filter and extension to Shannon’s channel capacity[J]. Digital Signal Processing, 2009, 19(5): 861-873.

[4] WU Lenan, FENG Man. On BER performance of EBPSK-MODEM in AWGN channel[J]. Sensors, 2010, 10(4): 3824-3834.

[5] FENG Man, WU Lenan, et al. BER analysis and verification of EBPSK system in AWGN channel[J]. IEICE Trans Commun, 2011, E94-B(3): 806- 809.

[6] WALKER H R. Ultra Narrow Band Modulation Textbook[EB/OL]. [2012-01-08] http://www.vmsk.org/

[7] WU Lenan, FENG Man, QI Chenhao, et al. Recent patents on ultra narrow band modulations[J]. Recent Patents on Signal Processing, 2011, 1(1): 36-47.

[8] MITOLA J, MAGUIRE G Q. Cognitive Radio: Making software radios more personal[J]. IEEE Personal Communications, 1999, 6(4): 13-18.

[9] 吴乐南, 应鹏魁. 扩展的二元相移键控调制参数性能比较[J]. 电波科学学报, 2011, 26(5): 961-965.

WU Lenan, YING Pengkui. Extended BPSK comparison with various modulation parameters[J].Chinese Journal of Radio Science, 2011, 26(5): 961-965.(in Chinese)

[10] 杨东凯, 吴华森, 张其善. AWGN信道中超窄带调制VMSK的最佳解调性能[J]. 通信学报, 2008, 29(5): 128-132.

YANG Dongkai, WU Huasen, ZHANG Qishan. Best performance of UNB modulation VMSK in AWGN channel[J]. Journal on Communications, 2008, 29(5): 128-132.(in Chinese)

[11] 徐淑正, 张 鑫. VWDK调制真的可实现吗? [J]. 电子与信息学报, 2009, 31(8): 1985-1989.

XU Shuzheng, ZHANG Xin. VWDK: Just an illusion?[J]. Journal of Electronics & Information Technology, 2009, 31(8): 1985-1989.(in Chinese)

[12] WANG Youguo, WU Lenan. Noise-improved signal correlation in an array of autoregressive models of order one[J]. Fluctuation and Noise Letters, 2007, 7(4): L449-L459.

[13] 张 嵩, 芮国胜, 孙文军, 等. EBPSK 信号混沌振子检测原理与性能分析[J]. 中国电子科学研究院学报, 2011, 6(5): 485-498.(in Chinese)

ZHANG Song, RUI Guosheng, SUN Wenjun, et al. Principle and performance analysis ofchaotic demodulator for EBPSK signals[J]. Journal of CAEIT, 2011, 6(5): 485-498.(in Chinese)

[14] 冯 熳, 高 鹏, 吴乐南. 超窄带调制信号的特殊滤波分析与仿真[J]. 东南大学学报:自然科学版, 2010, 40(2): 227-230.

FENG Man, GAO Peng, WU Lenan. Analysis and simulation of special filtering based on ultra narrow band modulated signal[J]. Journal of Southeast University: Natural Science Edition, 2010, 40(2): 227-230.(in Chinese)

[15] YAN Kaokao, WU Lenan. Impacting filter design: From digital to analog[J]. International Journal of Research and Reviews in Soft and Intelligent Computing(IJRRSIC), 2011, 4(1): 98-100.

[16] 陈晓毅, 姚庆栋, 刘小成. 高效数字调制VMSK的错觉[J]. 电子与信息学报, 2003, 25(11): 1558- 1563.

CHEN Xiaoyi, YAO Qingdong, LIU Xiaocheng. The vmsk modulation delusion[J]. Journal of Electronics & Information Technology, 2003, 25(11): 1558- 1563.(in Chinese)

[17] 何善宝, 林益明, 吴乐南, 等. 星间链路新型信号体制设计[J]. 中国空间科学技术, 2011(4): 15-22.

HE Shanbao, LIN Yiming, WU Lenan, et al. Design of new signal system for inter-satellite links[J]. Chinese Space Science and T echnology, 2011(4): 15-22.

[18] 靳 一, 吴乐南, 冯 熳, 等. 一种随机极性MCP-EBPSK调制解调器[J]. 电子与信息学报, 2012, 34(7): 1647-1652.

JIN Yi, WU Lenan,FENG Man, et al. An MCP-EBPSK modem with random-polar[J]. Journal of Electronics & Information Technology, 2012, 34(7): 1647-1652.(in Chinese)