认知无线电中能效优先的多用户随机接入方法

甘小莺 陈时阳 王路洋 金荣洪

(上海交通大学电子工程系，上海 200240)

引 言

在认知无线电网络中[1-2]，无线资源有限，信道环境又具有时变性，因此，需要设计一种多用户随机接入方案，来协调用户之间的资源调度问题.Xin Liu等人[3]提出了一种基于时隙结构的机会调度方法，在这种时隙结构系统指定的一个时间段内，只有一个用户能够占用信道.该方法最重要的假设是调度者知道所有用户探测后的信道情况，也就是说，这种调度方案是集中式的.

在Ad-hoc网络中，当用户不知道其他参与者的信道情况时，就产生了分布式机会调度 (Distributed Opportunistic Scheduling, DOS) 问题.Dong Zheng等人[4-7]对分布式机会调度的吞吐量进行了研究，在他们提出的系统模型中，多个用户通过随机接入的方式竞争同一信道.在这样的网络中，DOS方案包括了联合信道探测和分布式的调度.上述研究考虑了完美和不完美信道信息以及时延约束等多种情况，然而，随着无线通信系统能耗问题的提出，仅分析系统的吞吐量，已经无法满足需求.

能耗被认为是评价系统效率的一个重要指标.随着网络服务数量的日益增加，可以预期将来通信系统的能耗会不断增长[8].提高能量效率，可以极大地降低能耗，同时也能够减轻影响全球的温室效应.

近年来，越来越多的科研人员开始关注能量效率的最优化问题.文献[9-10]研究了无线局域网(Wireless Local Area Networks，WLAN)中传输吞吐量和能量效率的关系，并讨论了传输吞吐量和能量效率同时达到最大化的问题.其中都使用了多用户竞争模型来建模WLAN的传输能耗.另外，文献[9]还分析了WLAN传输的能量特性对能量效率与吞吐量的影响.但是，上述多用户竞争模型并不是基于认知无线电网络的，没有考虑用户接入信道前的探测问题，也没有考虑用户接入信道时的资源调度问题.因此，将该模型直接应用到认知无线电领域，具有较明显的局限性.

为了分析认知无线电网络中随机接入算法的能量效率，论文首先提出了一种认知无线网络的能量消耗模型.随后，确立了以能量效率为目标函数的最大化问题，也就是最大化平均每焦耳能量下传输的比特数.当认知无线电网络工作在以网络为中心的模式时，所有的认知用户以最大化系统级能量效率为目标进行接入调度.通过运用最优停止原理[11]，可以证明，最优的接入和调度方案实际上是一个基于门限的判决准则，而该门限可以通过迭代算法来获得.在此基础上，还研究了能量效率最大化与吞吐量最大化之间的关系，并给出了使能量效率和吞吐量同时达到最大的充分条件.当认知无线电网络工作在以用户为中心的模式时，基于非合作博弈方法，给出了一种纳什均衡点的求解方法.最后，将用户为中心模式和网络为中心模式进行比较后发现，用户的自私行为会使系统级的能量效率下降.

1 系统模型

1.1 系统设置

考虑一个有M个认知用户的随机接入认知无线电网络.图1是一个有单个首要用户(Primary User, PU)和4个认知用户(Secondary User, SU)的认知网络[12].在首要用户未使用信道时，认知用户可以检测到信道空闲并使用该信道传输信息.文中，一个认知用户被看作是随机接入的一个候选者.首先，假设所有用户是经过同步的，即他们会在时隙开始阶段进行竞争、探测以及传输.在每次通信中，每位用户根据自身的传输需求以概率pm竞争信道；在竞争过程中，用户花费时间τ1来向所有认知用户广播一个极短的竞争数据包(见图2)，并通过监听数据包是否和其他用户发出的数据包发生碰撞来得到竞争结果.当有且仅有一个用户竞争信道时(该用户广播的竞争数据包没有发生碰撞)，该用户获得信道，一个竞争环节结束.S(n)表示在第n次竞争中成功的用户.假设用户对信道进行了Ki次竞争后，用户S(i)获得了信道，随后，它将会用时间τ2探测信道，并得到一个可能的传输速率RS(i).如果RS(i)能够满足停止标准，用户S(i)就会向其他认知用户广播一个数据包，表明该信道将被其用于数据传输，时长为T.那么，其他的用户将会保持空闲直到下一次竞争环节开始.如果用户S(i)发现其传输速度不满足停止准则，那么就会放弃使用该信道并以概率pS(i)进行随机退避，所有的用户将再次竞争这一信道.假设在τ1时间内有不止一名用户发送数据包竞争信道，则数据包将发生碰撞，所有用户将在接下来的τ2时间内保持空闲(这个空闲的τ2时间一般在微秒级别，作用是为了保证下一次所有用户的竞争仍然是同步的)，并进行随机退避，等待下一次竞争.如果没有用户在τ1时间内竞争，则该时隙被视为空闲.

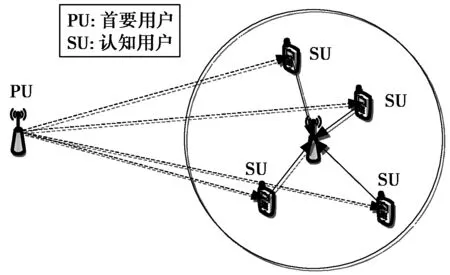
图1 认知无线电网络结构示意图

图2 传输回合示意图

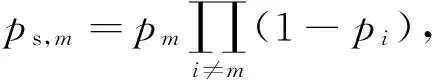
1.2 能量设置

假设每个用户的竞争功率、探测功率和传输功率分别为Pc、Pp和Pt,m，m=1,2,…,M.竞争功率和探测功率是统一的，而传输功率则取决于用户的信道状态.当一个用户空闲时，假设它不消耗能量.

由此可得

TE[Pt,S(N)],

(1)

假设N，Ki,Ci,i=1,2,…,是独立的，同时，Ki和Ci是同分布的.为了简化表示，这里用K和C代替.

2 分布式机会调度：以网络为中心的合作式优化

本节对联合探测与分布式机会调度进行研究.在网络为中心的模式下，能量效率的优化是系统级的.假设整个认知网络成功地进行了L次传输，那么系统级能量效率可以定义为

(2)

式中WNl是包含Nl个竞争环节的第l次传输回合的能量损耗.当L→∞时，能量效率η为

(3)

优化的目的是找出一种最优的停止准则N*，使得长时间下的能量效率最大化，表述如下：

(4)

2.1 最优停止原理

通过使用文献[11]中的最优停止准则，得到如下定理.

定理1最优停止准则N*存在并且有[11]

N*=min{n≥1:RS(n)≥η*Pt,S(n)},

(5)

式中η*是下列方程的唯一解：

(6)

由此可见，停止准则是一个基于门限的策略.在η*确定后，每一个用户都可以根据他们探测到的传输速率决定是否停止.当RS(n)不小于门限η*Pt,S(n)时，用户S(n)就会开始数据传输.否则，他会放弃这次机会，所有的用户开始新的一轮竞争.

假设Rm的累积分布函数(Cumulative Distribution Function, CDF)是Fm(r)，将这一结果带入定理1的结论，可以得到如下推论：

推论1在异构网络中，最大能量效率是下面方程的唯一解：

(7)

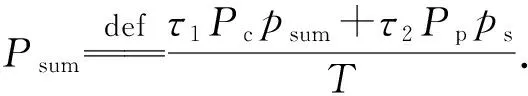
令

为了求解η=φ(η)，给出如下迭代算法[4]

ηk+1=φ(ηk),k=0,1,2,…，η0=0.

(8)

算法的收敛性证明见附录A.

2.2 能量效率与吞吐量的一致性讨论

当能量效率和吞吐量能够同时达到最大时，可以认为能量效率与吞吐量具有一致性.为了研究这个问题，首先，将等式(7)和文献[4]中吞吐量门限的表达式进行比较，即：

(9)

最大吞吐量x*是方程(9)的唯一解.

(10)

3 分布式机会调度：以用户为中心的非合作博弈

3.1 非合作博弈

当所有的认知用户行为表现为自私而不是合作时，需要在非合作环境下研究这种博弈.在这种设置下，每一个用户都希望最大化自己的能量效率，此时，仍旧可以运用最优停止原理来解决这一问题.在合作优化中，所有的用户具有同一个门限，然而，非合作博弈给出的解是一个向量η=(η1,η2,…,ηM)，而对应的每一个用户的传输速率门限为(η1Pt,1,η2Pt,2,…,ηMPt,M).

根据最优停止原理[11]，如果用Fm(r)表示每个用户传输速率的CDF，并假设用户m的停止门限为ηmPt,m，那么用户m的平均能量效率可以表示为

(11)

现在，可以把以用户为中心的非合作博弈定义为

(12)

3.2 纳什均衡点的迭代求解

定义1向量η可以定义为一个纳什均衡当且仅当对于任意的用户m有

(13)

基于文献[13]的方法，可以认为当方程

(14)

成立时，式(12)存在纳什均衡点.同时，假设用户m根据式(15)更新它的门限：

ηm(k+1)=φm(η(k)),m=1,2,…,M,

(15)

则该算法收敛到一个纳什均衡点[4].

4 数值结果分析

假设用户的传输速率由香农信道容量给出

R=ln(1+ρh2)nats s/Hz

(16)

式中：ρ是系统信噪比(Signal to Noise Ratio, SNR)；h是瑞利分布中相应的信道衰落.得到用户m上传输速率的累积分布函数为

(17)

4.1 合作优化的数值结果

将式(17)代入式(7)，可以得到

(18)

表1 异构网络用户接入参数

表2 异构网络用户传输功率Pt,m

根据式(8)中的迭代算法，数值解将会在迭代后收敛到最大能量效率η*，图3给出了异构网络中求解η*的迭代步骤和结果.

图3 异构网络中求解η*的迭代步骤和结果

根据推论1可知，图3中点划线y=φ(η)和实线y=η的交点是(η*,η*)，η*表示最大能量效率.虚线轨迹表示收敛路径.

图4给出了异构网络中能量效率和吞吐量之间的关系.为分析能量效率与吞吐量的一致性，首先假设每个用户的传输功率相同且为Pt，同时有Pt=100 mW，Pc=Pp=5 mW.在图4中，当传输速率停止门限从0向∞增大时，蓝色曲线从黑色标记处开始延伸到坐标轴的原点.在速率门限取确定值时，纵轴表示其能量效率，横轴表示其吞吐量.计算吞吐量的方法参见文献[4]中的式(35).图4中的红色圆点和红色方点分别表示取得最大能量效率处和取得最大吞吐量处.可以发现，当能量效率取得最大值时，吞吐量不能取得最大值，反之亦然.

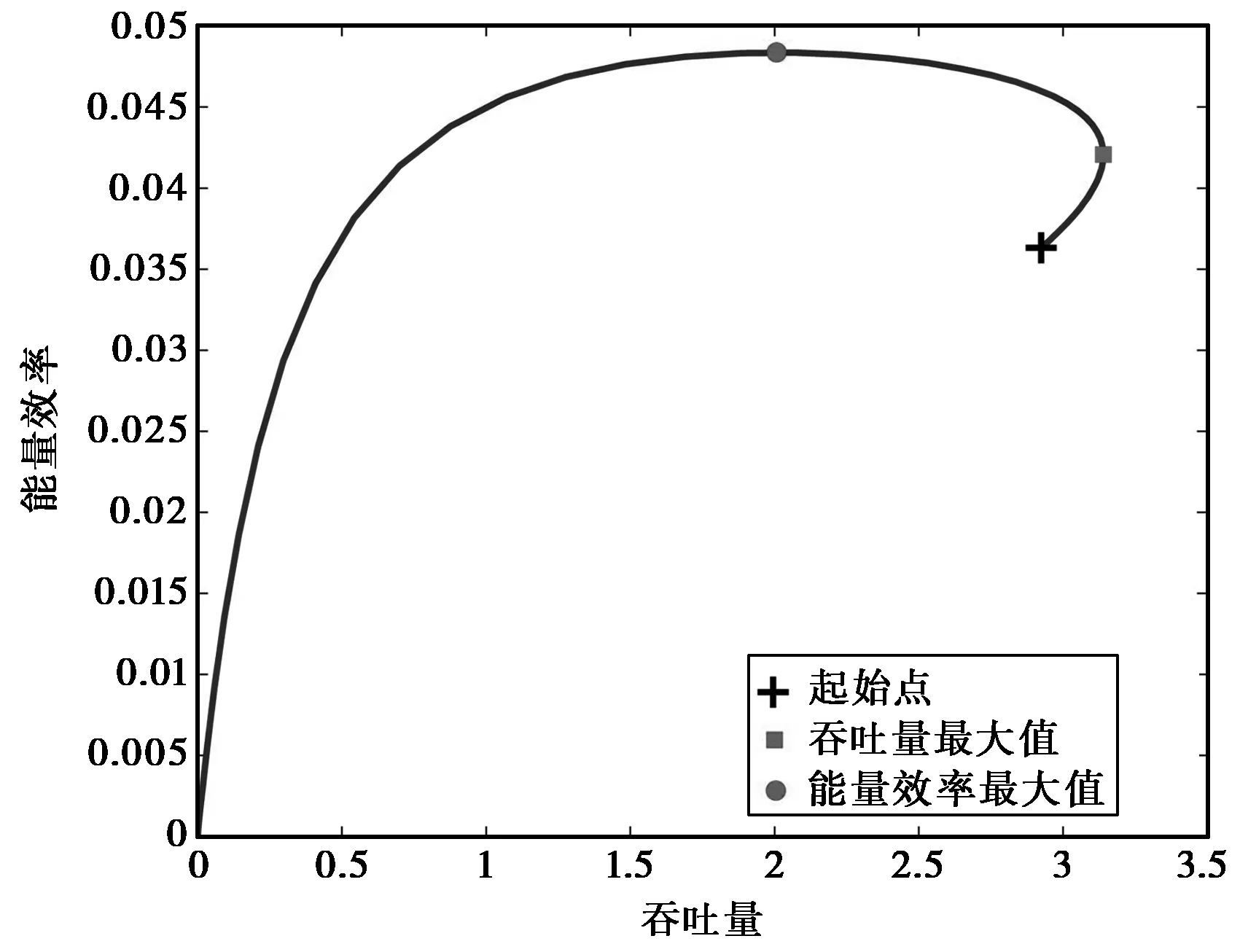
图4 异构网络中能量效率和吞吐量之间的关系

图5给出了Pt改变时能量效率和吞吐量的关系.在图5中，设定Pc=Pp=5 mW不变，并改变传输功率.数值计算结果显示，当Pt=5 mW时，两个最大点几乎相互重叠，此时τ1Pcpsum+τ2Ppps≈(τ1+τ2)Pt，也就是基本符合吞吐量和能量效率一致性的充分条件(10).因此，最大能量效率和最大吞吐量可以在Pt=5 mW处同时达到.但是，当Pt较小时(Pt=0.5 mW)，两个最大点之间的距离非常明显.从图5可以看出：当系统吞吐量最大时，会牺牲11%的能量效率；当系统能量效率最大时，吞吐量损失为5%.因此，当Pt比较小时，应该重点关注最大化能量效率，这样，既能得到最大的能量效率又不损失过多的吞吐量.当Pt比较大时(Pt=20 mW)，应该重点关注最大化吞吐量，这时能量效率的损失会很小.

图5 Pt改变时能量效率和吞吐量的关系

图6给出了Pc和Pp给变时，能量效率和吞吐量的关系.在图6中，设置Pt=5 mW，由图可见，当τ1Pcpsum+τ2Ppps≈(τ1+τ2)Pt时，能量效率最大点与吞吐量最大点重合.此外，当Pc和Pp取值较小时(Pc=Pp=0.1 mW)，应该重点关注吞吐量的最大化，而当Pc和Pp取值较大时(Pc=Pp=100 mW)，应该关注能量效率的最大化.

图6 Pc和Pp改变时能量效率和吞吐量的关系

4.2 非合作博弈的数值结果

图7给出了异构网络中，非合作博弈相对合作优化在能量效率上的损失.首先，在0和0.5之间生成1 000个随机数.当用户数增加时，从中选出一个数来表示新用户的竞争概率pm.参数设置如表3所示.

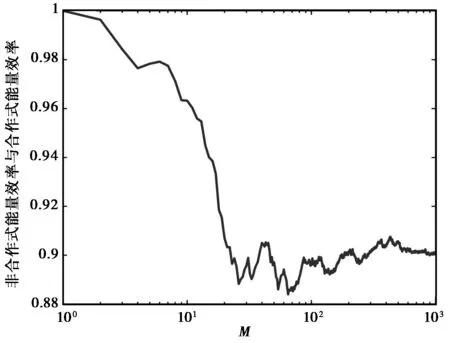
图7 能量效率的损失和用户数的关系

Pt,m/mWPc/mWPp/mWτ1/sτ2/sT/s5110.070.031

在图7中，纵轴代表非合作博弈与合作优化的系统级能量效率之比，横轴表示用户数.由图7可见：当用户数趋近于无穷时，比值将会收敛到0.9.同时，图7的曲线存在波动，这是因为增加了新的用户会影响到系统的参数配置，而在异构网络中，纳什均衡点并不唯一，因此，从一个纳什均衡点变到另一个纳什均衡点，就引起了曲线的波动.尽管如此，曲线的收敛趋势依然很清楚.

5 结 论

论文提出了一种能效优先的多用户随机接入方法.该方法利用最优停止理论，能够实现接入算法能量效率的最大化.在此基础上，论文推导了使能量效率和吞吐量同时达到最大的充分条件.数值计算结果表明：当传输功率与竞争功率和探测功率相比足够小时，算法能够在最大化能量效率的同时不损失过多的系统吞吐量.反之，如果传输功率远大于信道竞争功率和探测功率，则当系统实现吞吐量最大化时，能量效率损失较小.此外，论文还研究了用户行为对能量效率的影响.当用户数增大时，由用户行为自私性带来的相对损失百分比小于10%.作者下一步将对非合作博弈的纳什均衡点特性进行分析，以发现具有帕累托最优(Pareto Optimal)的纳什均衡点.

附录A

收敛性证明如下：

正文图3中，两条曲线分别为y=φ(η)和y=η，两者相交且只有一个交点(由推论1得).又经计算得φ(0)>0且φ(+∞)=0，所以两条曲线的关系如图3所示.

对于迭代的中间步骤，如果ηi<η*，则ηi+1=φ(ηi)≤φ(η*)=η*，这意味着，在迭代过程中，一旦有一个ηi在η*左侧，则ηj,j>i将一直保持在η*左侧.所以，当初始点设置为η0=0<η*时，根据以上证明可以知道，ηi≤η*,k=0,1,2,….又因为，y=φ(η)和y=η有且只有一个交点，且φ(0)>0，所以当η<η*时，φ(η)>η.于是，ηi+1=φ(ηi)>ηi.综上所述，{ηi}是一个递增，且有上界，因此，数列{ηi}一定收敛.

接着，将ηi+1=φ(ηi)改写为

Fm(ηPt,m)))).

(A1)

(A2)

至此，可以得到结论，这种递归的方法收敛，并收敛于η*.

证毕.

[1] 王 莹, 岳殿武, 王 谦, 等. 基于信道统计特征的认知无线电协作频谱检测[J]. 电波科学学报, 2009, 24(6): 1049-1054.

WANG Ying, YUE Dianwu, WANG Qian, et al. Channel statistics based cooperative spectrum sensing for cognitive radios[J]. Chinese Journal of Radio Science, 2009, 24(6): 1049-1054. (in Chinese)

[2] 马忠贵, 周贤伟. 基于自适应智能天线的认知无线电抗干扰方法[J]. 电波科学学报, 2010, 25(4): 767-772.

MA Zhonggui, ZHOU Xianwei. Interference suppression method in cognitive radio networks based on adaptive smart antenna[J]. Chinese Journal of Radio Science, 2010, 25(4): 767-772. (in Chinese)

[3] LIU X, CHONG E K P, SHROFF N B. A framework for opportunistic scheduling in wireless networks[J]. Computer Networks, 2003, 41(4): 451-474.

[4] ZHENG D, GE W, ZHANG J. Distributed opportunistic scheduling for ad hoc networks with random access: An optimal stopping approach[J]. IEEE Transaction on Information Theory, 2009, 55(1): 205-222.

[5] ZHENG D, PUN M O, GE W, et al. Distributed opportunistic scheduling for ad hoc communications with imperfect channel information[J]. IEEE Transaction on Wireless Communications, 2008, 7(12): 5450-5460.

[6] ZHENG D, PUN M O, GE W, et al. Distributed opportunistic scheduling for ad-hoc communications under noisy channel estimation[C]// IEEE International Conference on Communications. Beijing, May 19-23, 2008: 3715-3719.

[7] TAN S S, ZHENG D, ZHANG J, et al. Distributed opportunistic scheduling for ad-hoc communications under delay constraints[C]// 2010 Proceedings IEEE INFOCOM. San Diego, March 14-19, 2010:1-9.

[8] VAN DER PERRE L, VAN THILLO W, DEJONGHEET A, et al. Tomorrow’s wireless communication requires higher throughput and a small energy budget[J/OL]. Chip Design Magazine. 2010 [2012-09-27]. http://chipdesignmag.com/display.php?articleId=4214&issueId=39

[9] SERRANO P, GARCIA-SAAVEDRA A, HOLLICK M, et al. On the energy efficiency of IEEE 802.11 WLANs[C]// ACM/IEEE Int Conf Mobile Comput. Lucca, April 12-15, 2010: 932-939.

[10] BRUNO R, CONTI M, GREGORI E. Optimization of efficiency and energy consumption in p-persistent csma-based wireless lans[J]. IEEE Transactions on Mobile Computing, 2002, 1(1):10-31.

[11] FERGUSON T S. Optimal Stopping and Applications [M/OL]. 2006 [2012-09-27] http://www.math.ucla.edu/ ～tom/Stopping/Contents.html

[12] 王 超, 刘 涛, 杜利平, 等. 一种新的认知无线电主用户信号识别方法[J]. 电波科学学报, 2009, 24(6): 1119-1123.

WANG Chao, LIU Tao, DU Liping, et al. A new method for recognizing the primary user in cognitive radio[J]. Chinese Journal of Radio Science, 2009, 24(6): 1119-1123. (in Chinese)

[13] OSBORNE M, RUBINSTEIN A. A Course in Game Theory[M]. Cambridge: the MIT Press. 1994.