基于C60分子结构共形球面多波束天线的研究

徐俊珺 姜 兴 黄明华

(桂林电子科技大学信息与通信学院，广西 桂林 541004)

引 言

在卫星通信系统中，对天线波束覆盖角度要求较宽、天线的增益要求较高.传统的平面阵列天线通常只能覆盖±60°范围[1]，无法满足波束覆盖的要求.球型结构具有空间的完全轴对称性，可以克服平面阵扫描角度小的缺点，将天线波束覆盖范围扩展到±90°，并在此范围内能保持天线的增益、波束宽度不变[2-3].考虑采用球面结构，利用球面排列的天线单元形成子阵产生多个波束来覆盖整个用户区域.多波束切换天线属于空分多址技术，它通过对天线子阵输出的信号进行幅相加权，产生空间定向波束，使天线主波束对准用户信号到达方向[4].当每个单元放置在曲面上，单元的最大辐射方向指向曲面的法线方向，阵元间的互耦也能得到改善[5].共形球面阵列天线能够满足卫星通信系统中空中平台天线对波束覆盖的要求，当阵列较大、阵元数目加多时，它在设计、研制上往往比普通的平面阵复杂；对它的分析需要在三维坐标系下进行，并且单元天线的幅相加权值不仅与波束指向有关，还与每一阵元的位置有关；同时，由于阵元安置在曲面上，各阵元方向函数的最大指向不同[6]，通常的方向图乘积定理不适用于共形阵，这就增加了计算或综合方向图的困难，在这方面的研究相对较少[7-8].本文的工作是设计了一种基于球面排列的由五边形和六边形组合的C60多平面天线结构，推导了球面阵阵因子的方向函数，对该阵列的结构特点进行分析，并对其进行多波束的仿真研究.

1 建立球面共形阵列模型

天线单元在球表面沿着轴对称以C60分子结构分布，球面阵的阵元如图1所示排列，六边形和五边形的组合图形形式分布在半径为R的球面上.多平面表面与其对应的球面具有良好的近似性，它的近圆对称性使辐射波束自然地接近圆形.由于阵元的分布受到共形载体外形的限制[9]，分析的时候通常在三维坐标系下进行.在分析球面阵的阵因子时，考虑应用投影法先将三维模型问题投影到二维平面上,应用同心圆环阵的阵因子，再加上俯仰角θ对应的参数变化即可求出.球面阵二维投影的几何结构如下图2所示[10]，N个阵元均匀分布在二维平面中的同心圆周上.

图1 共形球面阵的C60分子几何结构

图2 二维投影的同心圆环模型

如图2所示，球面上的在每一个圆环单元可以按圆环阵的方向函数来分析，假设N个单元对于观测点P(R,θ,φ)都是可见的，即不考虑由于曲率而导致的天线单元被球体全部或部分遮挡的情况，设球面阵的半径为a，每n个圆环对应的空间俯仰角为θn.每一个圆环的半径为b=asinθn，电流的振幅为Inm，每个单元天线的方向函数为f(θ′,φ′)，圆环上对应的每一阵元的方位角为φnm，下角标n表示第n环，m表示每一环上的第m个单元.激励电流的相位为e-jΨnm.当考虑观测点为无穷远处，R≫a，假设观测点到球面中心与到每一圆环的中心距离近似相等，r为观测点到天线单元的距离，圆环上各单元与球心之间的波程差[11]为

R-r=asinθnsinθcos(φ-φm)+acosθcosθn

(1)

求出球面阵的阵因子

φnm)+cosθcosθn]+jΨnm}

(2)

图3 共形球面阵的坐标及空间变量

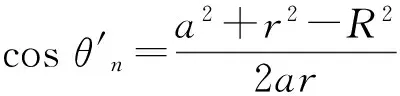
(3)

cosθcosθn)/2aR

≈sinθnsinθcos(φ-φm)+cosθcosθn

(4)

cosθcosθn).

(5)

r在(o′x′y′)面上的投影为

(6)

r在x′轴上的投影为,Rcosθsinθn

(7)

(8)

圆环球面阵在远区的合成辐射场为

cos(φ-φnm)+cosθcosθn]+jΨnm}

(9)

2 C60结构球面天线的特点及波束的仿真研究

C60分子结构是由12个正五边形环和20个正六边形环的球形三十二面体构成(又称截角二十面体).它可以看作是在正二十面体上截去12个顶角后在新的顶角位置放上60个单元形成的球形32面体(图4).顶角截去后得到12个五边形，原来的20个面则形成六边形，在每一个定点位置放置一个天线单元，每个顶点所连接的3个单元组成一个天线子阵.这种结构的特点是：每一个顶点单元到与之相连接的3个单元的空间距离是相等的；正五边形和正六边形的内角分别为108°和120°，顶点到其他3个单元的空间夹角分别为120°、120°和108°.

图4 正二十面体截去顶角后在每个顶角点位置放入5个单元形成的球形32面体

对半球面结构多平面天线的具体尺寸进行分析：半球型C60结构(30个单元)，按圆环角度分析采用4层圆环分布，每一环的阵元分别为5、5、10、10元(图2).最外环的10元不能再形成顶点，整个半球形成20个单元子阵，由于球结构的完全轴对称性分布，每个子阵的结构是相似的，产生的波束的特性也是相似的，仅需要分析单元子阵的波束特性即可.首先，设球的半径为R，第一圆环的俯仰角为θ1，第一圆环和第二圆环呈圆内接正五边形，阵元间投影夹角为108°，设球面每个单元天线的空间距离L满足L=2sin 36°·R·sinθ1，第二圆环的俯仰角为θ2，L=2R·sinθ2/2，并且sin(θ1+θ2)=2sinθ1，求出θ1=20.07°，θ2=23.35°，L=0.404R，以此类推θ3=15.65°，θ4=21.12°，半球形C60结构天线阵的空间张角为80.19°，由于顶点单元到与之相连接的3个单元的空间距离是相等的，每个单元到顶点的张角为23.3°(图5).图6给出了单元天线的方向图，通过函数拟合得到单元的方向性函数f(θ′,φ′)， 并带入到球面阵的方向函数中(方程9)，利用阵列方向图综合的自适应算法，得到一个在子阵顶点的法向方向为最大辐射方向的波束，波束俯仰角为15.6°，见图7.表1给出子阵中单元的幅度和相位的加权因子.

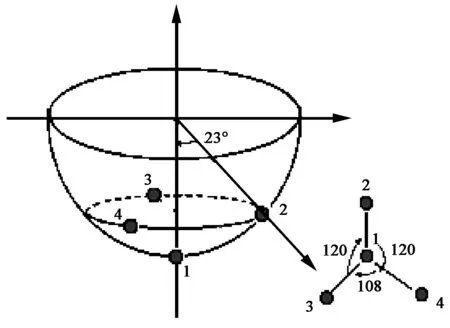
图5 单元子阵的空间分布

图6 单元天线方向图

图7 4单元天线子阵方向图

幅相单元1单元2单元3单元4振幅21.21.21.2相位/(°)0-3582-82

3 结 论

本文设计了一种基于C60分子结构排列、在波束的覆盖范围及阵元间距一定的条件下构造了球面对称分布的多平面共形阵模型.推导了球面阵因子以及共形单元在坐标系的阵因子方向函数，并对其结构进行了分析和仿真.利用自适应加权算法，天线子阵单元能够形成一个在子阵顶点的法向方向为最大辐射方向的波束.通过研究，对复杂的共形阵列的建模问题提供了有益的启示，也为今后多波束形成提供了参考.

[1] ZHOU P Y, INGRAM M A. Pattern synthesis for arbitrary arrays using an adaptive array method[J]. IEEE Transaction on Antennas and Propagation, 1999, 47(5): 862-869.

[2] 陈腾博, 陈轶博, 焦永昌, 等.采用非线性最小二乘法实现圆环天线阵的方向图综合[J].微波学报, 2005, 24(1): 1-4.

CHEN Tengbo, CHEN Yibo, JIAO Yongchang, et al. Synthesis of the circular antenna array by the nonlinear least square method[J]. Journal of Microwares, 2005, 24(1): 1-4. (in Chinese)

[3] 欧阳骏, 杨 峰, 聂在平, 等.基于遗传算法的载体上共形天线阵列优化[J]. 电波科学学报, 2008, 23(2): 356-359.

OUYANG Jun, YANG Feng, NIE Zaiping, et al. Optimizing design of conformal antennas array on platform with GA method[J]. Chinese Journal of Radio Science, 2008, 23(2): 356-359. (in Chinese)

[4] CHUNG Y C, HAUPT R. Low side lobe pattern synthesis ofspherical arrays using a genetic algorithm[J]. Microwave and Optical Technology Letters, 2002, 32(6): 751-754.

[5] WETTERGRN T A. Element directivity compensation for beam forming a curved array[J]. IEEE Signal Processing Letters, 2004, 11(10): 854-848.

[6] 杨 鹏, 杨 峰, 聂在平, 等.MUSIC算法在圆柱共形天线阵DOA估计中的应用研究[J]. 电波科学学报, 2008, 23(2): 288-291.

YANG Peng, YANG Feng, NIE Zaiping, et al. DOA estimation of cylindrical conformal array by MUSIC algorithm[J]. Chinese Journal of RadioScience, 2008, 23(2): 288-291. (in Chinese)

[7] HUANG Z Y, BALANIS C A. Adaptive beamforming using spherical array[C]//IEEE Antenna and Propagation Society Interna-tional Symposium, 2005, 4A: 126-129.

[8] 张 奋. 圆柱共形微带天线的设计与研究[D]. 西安: 西北工业大学, 2006.

ZHANG Fen. Design for Cylindrical Conformal Microstrip Antenna[D]. Xi’an: Northwestern Polytechnical University, 2006. (in Chinese)

[9] 毛文辉,朱 旗,王少永, 等. 宽波束柱面共形毫米波微带天线设计[J]. 电波科学学报, 2008, 23(2): 272-275.

MAO Wenhui, ZHU Qi, WANG Shaoyong, et al. Design of cylindrical conformal millimeter-wave microstrip antennas with broad beamwidth[J]. Chinese Journal of Radio Science, 2008, 23(2): 288-291. (in Chinese)

[10] FRANEK O, PEDERSEN G F, ANDERSEN J B. Numerical modeling of a spherical array of monopoles using FDTD method[J]. IEEE Trans on Antennas and Propagation, 2006, 54(7): 1952-1963.

[11] 杨继波, 陈客松, 胡进峰, 等. 球面阵列的阵元分布及副瓣特性分析[J]. 中国电子科学研究院学报, 2009, 14(6): 584-588.

YANG Jibo, CHEN Kesong, HU Jinfeng, et al. Spherical antenna array element distributions and analysis of the sidelobe characteristic[J]. Journal of China Academy of Electronics and Information Technology, 2009, 14(6): 584-588.(in Chinese)