高技术产业与经济增长关系的实证分析

张华平

（华北水利水电学院，郑州 450011）

0 引言

近年来，我国高技术产业快速发展，高技术产业增加值由1995年的1080.52亿元增加到2010年的16571.34亿元，年均增长20%；同时，我国总体经济水平保持高速增长。2010年国内生产总值（GDP）达397983亿元，同比增长10.3%。自1995年以来，我国高技术产业增加值和GDP都呈现快速增长趋势，但是二者是否存在着互为因果的关系？它们彼此之间会产生什么样的冲击？为回答这些问题，本文以1950～2010年的时间序列数据，采用动态计量模型检验二者的关系，为促进高技术产业与经济增长的协调发展提供参考。

1 变量选取与数据处理

本文的研究涉及二个变量，即高技术产业发展与经济增长。在度量指标的选取上，着重考虑以下几点：一是指标代表性，即指标能反映变量的本质特征；二是数据可获性，即指标数据便于获取和更新；三是简明性，即指标应尽可能的少，易于推广应用。关于高技术产业发展的衡量，相关指标很多，如高技术产业新产品总产值、工业销售额、主营业务收入等。结合高技术产业发展的内涵，选取目前应用最为广泛的“高技术产业增加值（单位：亿元）”来度量高技术产业发展状况，反映高技术产业新创造财富和附加值的高低。考察经济增长的最常用指标是国内生产总值（单位：亿元），对一国总体经济运行表现作出的概括性衡量，具有国际可比性，是联合国国民经济核算体系中最重要的总量指标。

上述指标数据来自《中国科技统计年鉴》、《中国统计年鉴》或者通过计算获得，考虑到指标数据的统计时期，选取样本空间为1995～2010年，具体数据如表1所示。为了消除物价变动对高技术产业增加值和国内生产总值的影响，利用表1中的以1995年为基期的价格指数（%）对它们进行平减，得到相应的实际变量。

同时，为了消除数据中存在的异方差，分别对各实际变量取对数，即：LHTI=log(HTI)，LGDP=log(GDP)；计算LHTI与LGDP的相关系数，如表2所示。高技术产业增加值与国内生产总值的相关系数为0.987495，呈现高度相关，反映它们之间的密切关系，说明建立计量经济模型来解释它们之间的关系是比较合适的。

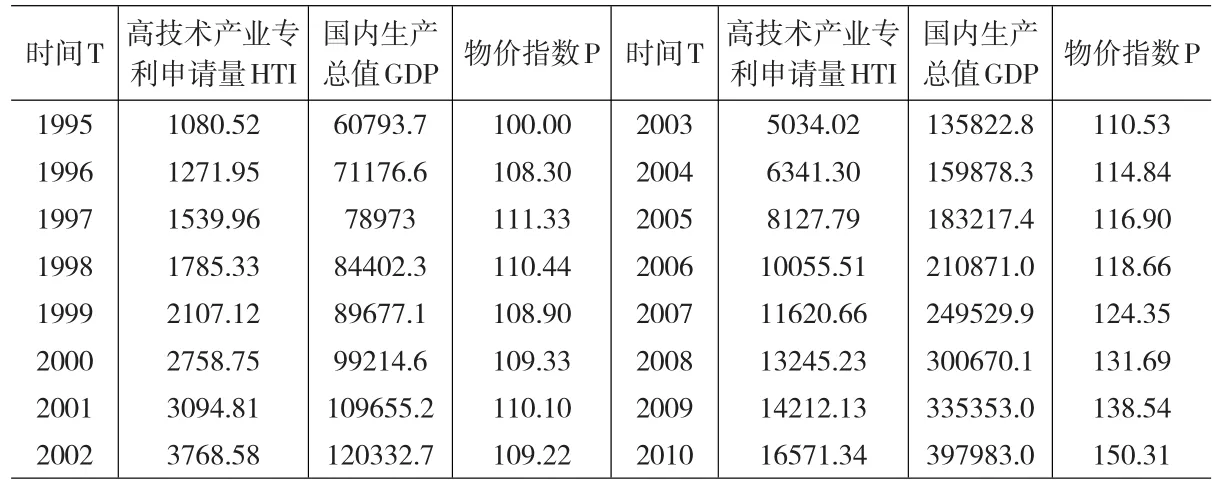
表1 各变量原始数据

表2 LHTI与LGDP相关系数表

2 计量模型与分析方法

本文利用计量经济学中的协整理论、格兰杰因果检验、误差修正模型及方差分解等方法，从以下五个方面验证高技术产业发展与经济增长之间的长期均衡关系和双向动态作用。

2.1 平稳性检验

考虑到经济现象大多数的时间序列是非平稳序列，易出现“伪回归”问题。故在建立模型前，需要对数据的平稳性进行单位根检验。检验方法主要有DF检验、ADF检验、PP检验、ERS检验和NP检验等，在实际应用中，ADF检验法更为常见。

2.2 协整关系检验

若非平稳性序列存在同阶单整，则可以对其进行协整分析。常用的协整检验方法包括EG两步检验法和Johansen协整检验法，前者适用于双变量协整检验，后者适用于多变量（＞2）协整检验。如果变量间存在协整关系，表明它们之间存在长期稳定的均衡关系。

2.3 误差修正模型

根据Granger定理，一组具有协整关系的变量一定存在误差修正模型。将协整方程的误差修正项作为引入变量，建立误差修正模型（ECM），用以解释变量由于某种原因短期偏离长期均衡的调整机制。

2.4 格兰杰因果检验

协整检验表明了变量之间存在长期均衡关系，但无法揭示变量之间是否存在因果关系及影响方向，格兰杰因果检验为解决此问题提供了方法和思路。一般地，如果变量X是变量Y的（格兰杰）原因，则X的变化应先于Y的变化。

2.5 方差分解

为了进一步研究我国高技术产业与经济增长之间相互作用的动态过程，本文对模型采用方差分解的技术方法，即将系统的预测均方误差按其成因分解为自身冲击、其它变量冲击所构成的贡献率，从而了解各变量冲击对模型内生变量的相对重要性。

3 实证过程

由图1可见，LHTI和LGDP的折线图带有明显的趋势性，可能是非平稳序列。因此，需要对序列进行平稳性检验。

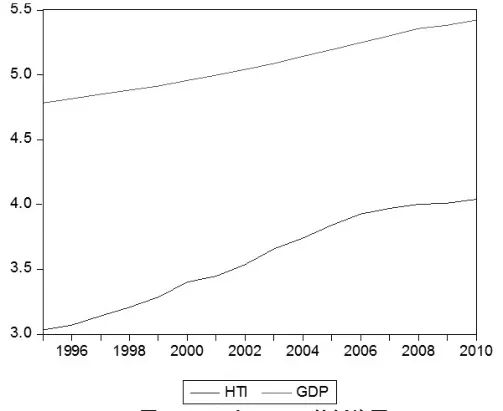
图1 LHTI和LGDP的折线图

3.1 单位根检验

本文采用ADF检验法对LHTI、LGDP及其差分项序列进行单位根检验，见表3。结果表明：时间序列变量LHTI、LGDP均属于非平稳的时间序列，其一阶差分变量iLHTI和iLGDP仍然属于非平稳时间序列，但其二阶差分变量iiLHTI和iiLGDP却成为了平稳的时间序列，因此，LHTI和LGDP均是二阶单整序列。

3.2 协整关系检验

分析表明LMJ和LYM均为二阶单整，故可以继续进行协整分析。本文采用选用EG两步检验法来检验LHTI和LGDP的长期关系。

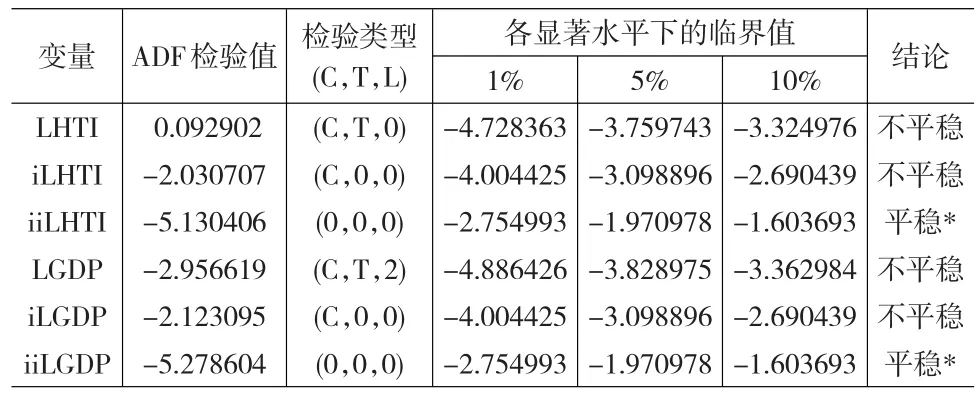
表3 平稳性检验结果

首先对LHTI和LGDP进行回归分析，并对其残差序列进行平稳性检验(括号内的数为t检验值)，得到协整方程为：

其次，令E表示协整方程的残差序列，对协整方程残差项进行单位根检验，结果见表4。

表4 协整方程残差项ADF检验

检验结果表明：在5%的显著水平下，LHTI和LGDP存在协整关系，即存在长期均衡。

3.3 消除自相关

在LHTI和LGDP关系协整分析时，发现方程的DW值偏小（DW=0.5892），可能存在自相关问题。如图2所示，回归模型的残差存在着高度的正相关。同时，采用偏相关系数法对此进行检验，结果显示第1期偏相关系数的直方块超过虚线部分，表明方程残差项存在一阶自相关。

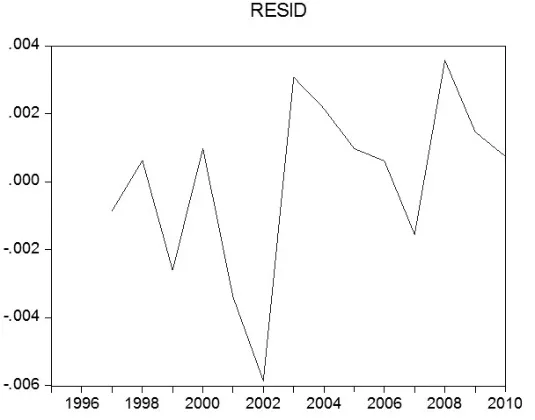
图2 回归模型的残差趋势图

为此，继续选用Cochrane-Orcutt迭代法消除自相关，得到LHTI和LGDP关系模型的最终协整方程为：

经检验，系数显著性、方程显著性及模型拟合度都良好，且不存在自相关和异方差。该方程显示，高技术产业增加值与GDP之间存在正相关的关系，高技术产业增加值每提高1个百分点，GDP将上升0.1604个百分点。

3.4 误差修正模型

利用LHTI和LGDP差分后的序列、各变量的滞后期以及初始方程残差项的滞后一期做回归分析，从一般到特殊的检验过程中，将统计上不显著的滞后变量逐渐剔除，最终得到反映高技术产业增加值与GDP之间短期动态均衡关系的误差修正模型：

误差修正模型各个变量通过了显著性检验，说明模型拟和效果较好。误差修正项系数小于0，符合反向修正原则。从短期来看，滞后一期的高技术产业增加值以0.1783的比率对当期经济增长产生负影响；滞后一期的非均衡误差以0.4342的比率对当期河南省经济增长作出修正，即经济增长的短期波动向长期均衡的调整力度为0.4342。

3.5 格兰杰因果检验

格兰杰因果关系检验对于滞后期长度的选择有时很敏感，不同的滞后期可能会得到完全不同的检验结果。本文利用信息法则即根据AIC和SC的数值大小将最优滞后阶数确定为2，检验结果见表5。

表5 Granger因果关系检验结果

结果表明，在5%的显著水平下，我国高技术产业发展与经济增长呈现出单向的格兰杰因果关系，即高技术产业发展是经济增长的格兰杰原因，但经济增长并不是高技术产业发展的格兰杰原因，表明我国高技术产业发展在一定程度上推动了经济增长，但经济增长并没有带来高技术产业发展。

3.6 方差分解

在Eviews中，根据VAR的输出结果绘制出表6和表7的高技术产业增加值和GDP的方差分解结果。

由表6发现，我国高技术产业增加值在第一期只受自身波动冲击的影响，从第二期开始直至以后各期来自其自身的扰动冲击逐渐缓慢下降；我国高技术产业增加值来自GDP的冲击是大体上逐渐上升的（除了在第五期略有下降外）。但是，无论从短期还是长期来看，我国高技术产业增加值波动受自身冲击的影响居于主导地位，受经济增长冲击的影响是有限的。该方差分解结果与前面的格兰杰因果检验的分析结论都是一致的。

表7显示，我国GDP的波动在第一期同时受到其自身和高技术产业增加值波动冲击的影响，之后各期来自其自身的冲击大体上呈现逐渐下降的趋势，而来自高技术产业增加值的冲击大体上呈现逐渐上升的趋势。从长期来看，高技术产业增加值变化的冲击能解释GDP变化的90%以上。同样，上述方差分解结果与前面的格兰杰因果检验的分析结论也是一致的。

4 结论

基于1995～2010年的时间序列数据，利用计量经济学中的协整理论、向量误差修正模型、格兰杰因果检验及方差分解技术，对我国高技术产业与经济增长关系进行动态分析，得出如下结论：

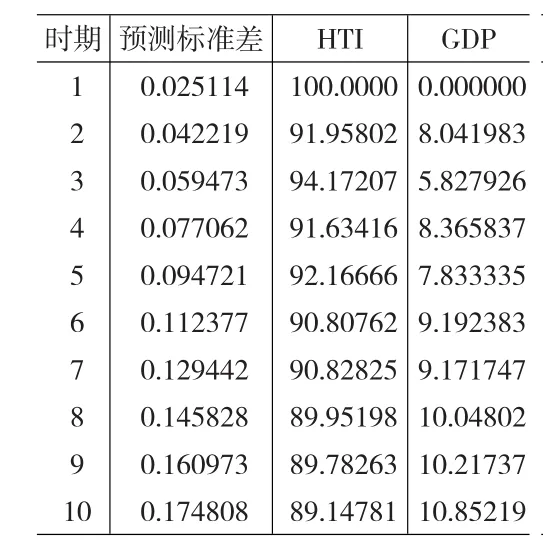
表6 变量HTI方差分解结果

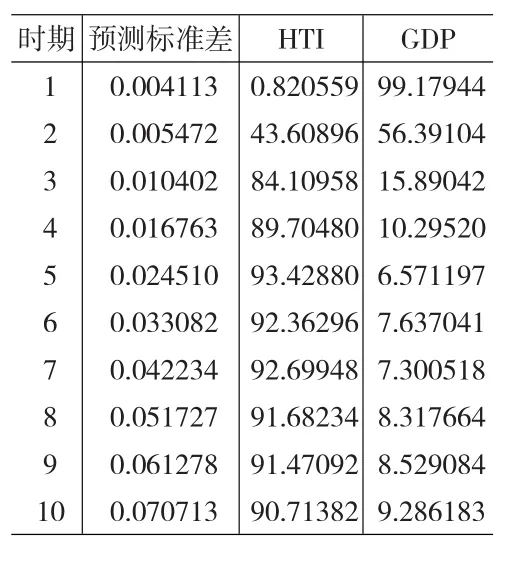
表7 变量GDP方差分解结果

（1）协整分析表明：我国高技术产业与经济增长之间具有协整关系，即存在长期稳定的关系。通过协整方程发现，我国高技术产业增加值每增加一个百分点，GDP将上升0.1604个百分点。显然，我国高技术产业对经济增长的推动作用是巨大的，经济增长对高技术产业的依赖性极强。

（2）误差修正模型表明：经济增长受自身或高技术产业的影响存在一定的滞后性。从短期来看，滞后一期的高技术产业增加值以0.1783的比率对当期经济增长产生负影响；滞后一期的非均衡误差以0.4342的比率对当期河南省经济增长作出反向修正。

（3）格兰杰因果关系检验表明：我国高技术产业与经济增长之间呈现单向的因果关系，即高技术产业是经济增长的格兰杰原因，但经济增长并不是高技术产业发展的格兰杰原因。说明我国高技术产业在某种程度上带动了经济发展，但是经济增长并没有推动高技术产业发展。

（4）方差分解结果表明：我国经济增长受高技术产业增加值冲击的影响占据主导地位，受自身冲击的影响有限；我国高技术产业发展主要受自身冲击的影响，受经济增长冲击的影响仅为10%左右。该分析结果与格兰杰因果检验结果是一致的。

综上，我国高技术产业与经济增长之间存在长期的均衡关系，但它们之间并没有形成良性互动。一方面，由于强烈的辐射效应，高技术产业带动关联产业发展，进而带来整个国民经济的发展。但是，另一方面，由于认识不到位、政策措施不配套，及我国产业构成比例不合理、技术创新环境薄弱等原因，制约了高技术产业发展，GDP增加并没有带来高技术产业增加值的提高。

[1]胡水晶.湖北高技术产业关联拉动经济增长研究[D].武汉：武汉理工大学,2009.

[2]梁丽丽.高技术产业对区域经济增长的贡献研究[D].合肥：合肥工业大学,2009.

[3]王晨,刘志蛟,张希等.上海市高技术产业与经济增长关联性的实证分析[J].科技风,2010,(9).

[4]王月嵩.高技术产业对经济增长的贡献度分析——以深圳市为例[J].现代商业,2011,(5).