住房保障领域中的一类非对称博弈问题分析

徐 江

（郑州大学管理工程学院，郑州 45000）

1 问题的提出

伴随快速城市化进程的是城市商品住宅价格的持续大幅快速上涨，以及城市弱势群体的日趋庞大，动辄数十万元甚至数百万元的房价使这一群体的住房问题逐步成为演变了重大的社会民生问题[1,2,3]。为此，国家相继出台了多项政策及措施来应对和解决城市弱势群体的住房保障问题，在住房体制改革纲领性文件的国务院（1998）《关于进一步深化城镇住房制度改革加快住房建设的通知》中，提出了要加快解决城镇住房困难的居民住房问题；到了2010年更是密集出台了大量的有关保障性住房建设的指导性文件，例如，国务院（2010）紧急出台《关于坚决遏制部分城市房价过快上涨的通知》，其中再次要求“加快保障性住房安居工程建设”；住建部等六部委（2010）联合印发的《关于做好住房保障规划编制的通知》要求到2012年末，需要基本解决1540万户低收入住房困难家庭的住房问题，力争到“十二五”期末，人均住房建筑面积13m2以下低收入住房困难家庭基本得到保障；国家七部委（2010）联合发布的《关于加快发展公共租赁住房的指导意见》指出要将城市中等偏下收入住房困难家庭、以及有条件地区的新就业职工和有稳定职业并在城市居住一定年限的外来务工人员，纳入公共租赁住房的供应范围。但是，从1998年开始至今，国家虽然一直强调要建立保障性住房供应体系，却远远没有达到应有的保障效果。由于对住房保障领域中各利益主体行为互动机理的分析研究还不够深入，住房保障政策未能充分有效地规范和制约这些利益主体的行为，是导致保障性住房建设进度缓慢、保障性住房遇冷的重要因素。本文从“有限理性”的演化博弈角度，探讨了住房保障领域中政府与城市弱势群体的非对称博弈问题，具体分析了两者理性程度的差异对于社会住房保障均衡收益的影响。

2 政府与城市弱势群体之间的博弈特征分析

传统博弈理论认为博弈参与人都是完全理性的。但是由于知识、信息等约束，人们在面对复杂问题时，可能有很大的理性局限（即有限理性）。“有限理性”(bounded rationality)的博弈参与人往往并不能在一开始就能做出最优策略，通常需要通过学习和试错等来寻找较好的策略；有限理性也意味着在博弈中至少有一部分博弈参与人不会采用完全理性博弈的均衡策略；有限理性还意味着博弈均衡可能在到达后再次偏离[4]。非对称博弈是在“有限理性”的不同特征参与人群体之间进行的演化博弈，由于支付矩阵是非对称的而得名。泽尔腾[5]首次探讨了有限理性的博弈各方的非对称博弈均衡问题，在引入角色限制行为的基础上提出了极限ESS，从而将传统的进化稳定策略引入到了非对称博弈，非对称博弈问题也因此可解。

2.1 模型的基本假设

政府与城市弱势群体之间关于住房保障政策的非对称博弈问题是一类个体参与者（政府）与群体参与者（城市弱势群体）间的非对称博弈。它的模型参数可设定如下[6,7]：

（1）a1为在政府采取“只说不做”的住房保障政策下，城市弱势群体进入非保障性住房市场，即“不信任并不等待”保障性住房时的收益；（2）b1为政府“只说不做”时的收益；（3）a2为政府推行“说到并做到”住房保障政策时，城市弱势群体采取“信任并等待”策略所享受到的住房保障政策收益；（4）-b2为政府“说到并做到”时的负收益；（5）a3为当住房保障成为社会共识后，城市弱势群体所获取的长期无形收益；（6）b3为推行“说到并做到”的住房保障政策给政府所带来的社会稳定、城市竞争力等方面的长期收益；（7）-a4为政府“只说不做”时，部分城市弱势群体仍然单方面“信任并等待”保障性住房的负收益；（8）b4为政府采取“只说不做”的住房保障政策时，因部分城市弱势群体采取“信任并等待”策略，而使政府意外获取社会暂时稳定等的收益。

假设初始状态时，城市弱势群体群体中采取策略A（“不信任并不等待”）的比例为x，采取策略B（“信任并等待”保障性住房）的比例为1－x；针对城市弱势群体的策略，政府采取策略M（“只说不做”）概率为y，采取策略N（“说到并做到”）概率为1－y。

根据以上设定的参数，构造双方的非对称博弈模型如图1示。

图1 政府与城市弱势群体间关于住房保障政策的非对称博弈模型

2.2 理性程度均等条件下的非对称博弈分析

政府与城市弱势群体的t次重复博弈，可以用模仿动态方程[6,7]（replicator dynamics equation）来模拟和分析。

由图1，城市弱势群体的期望收益为：

采取策略A(“不信任并不等待”)的期望收益G11＝ya1+(1-y)(a2-a1)；

采取策略B(“信任并等待”)的期望收益G12=y(a1-a4)+(1-y)(a2-a1+a3)；

群体平均期望收益G1=xG11+(1-x)G12；

政府的期望收益为：

采取策略M(“只说不做”)的期望收益G21=xb1+(1-x)(b1+b4)；

采取策略N(“说到并做到”)的期望收益G22=x(b3-b2-b1)+(1-x)(b3-b2)；

政府的平均期望收益G2=yG21+(1-y)G22；

双方的模仿动态方程分别为：

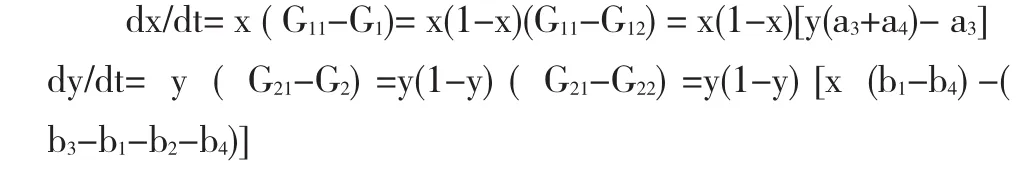
从模仿动态方程对城市弱势群体的博弈策略进行分析：当y*=a3/(a3+a4)时，dx/dt≡0，即政府真正推行住房保障政策，推行力度达到启动点y**＝1-y*＝a4/(a3+a4)时，城市弱势群体中进入非保障性住房市场与信任并等待的比例处于大致均衡的状态；当y＞y*时，x1=0与x2=1是两个稳定状态，其中，进化稳定策略是x2=1，即当政府不能“说到并做到”时，信任并等待保障性住房的城市弱势群体将逐步消失，进入非保障性住房市场将是群体共识；当y＜y*时，x1=0与x2=1仍然是两个稳定状态，其中，进化稳定策略是x2=0，即城市弱势群体“信任并等待”的策略与政府“说到并做到”的住房保障政策良性互动，并逐渐达到帕累托最优状态。

政府推行住房保障政策暗含了必须以政府信用、社会稳定、城市竞争力等的实际长期收益为重，即b3＞b1+b2+b4。当 x*=(b3-b1-b2-b4)/(b1-b4)时，dy/dt≡0，即当城市弱势群体“信任并等待”的比例达到临界点x**=1-x*=(2b1+b2-b3)/(b1-b4)时，政府“说到并做到”的住房保障政策处于稳定状态；其中，b3＜2b1+b2，这表明政府推行住房保障政策的长期收益是有边界的，住房保障政策不能解决所有的城市住房问题。当x＞x*时，博弈的稳定状态是y1=0与y2=1，其中，进化稳定策略是y2=1，即在城市弱势群体强烈“不信任并不等待”住房保障政策情形下，住房保障政策有逐步演变为“只说不做”的可能；当x＜x*时，y1=0与y2=1是博弈的稳定状态，其中，博弈的进化稳定策略是y2=0，即政府的“说到并做到”与城市弱势群体的“信任并等待”良性互动，达到了帕累托最优状态。

双方关于住房保障政策的非对称博弈演化趋势如图2所示。该博弈的进化稳定策略(ESS)为(1,1)和(0,0)，并且最终的博弈均衡情况取决于系统的初始状态。当博弈的初始状态落在区域Ⅳ中时，系统将逐步收敛到帕累托劣解(1,1)，即（不信任并不等待，只说不做）；当博弈的初始状态位于区域Ⅰ中时，系统将会逐步收敛到帕累托最优均衡(0,0)，即（信任并等待，说到并做到）；当初始状态落在区域Ⅱ、Ⅲ中时，系统演化的方向是不确定的，即有可能进入区域Ⅳ而收敛到(1,1)，也有可能进入区域Ⅰ而最终收敛到(0,0)。其中，x*=(b3-b1-b2-b4)/(b1-b4)与 y*=a3/(a3+a4)是该博弈结构特性变化的阚值。

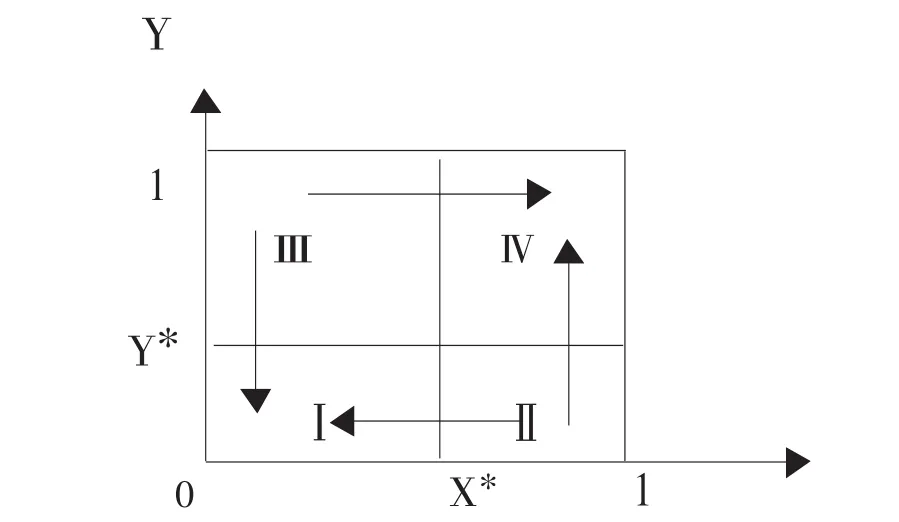
图2 住房保障政策的非对称博弈演化相位图

2.3 理性程度不等条件下的非对称博弈分析

从图1和图2中可以看到政府与城市弱势群体关于住房保障政策的非对称博弈仍然存在着多重Nash均衡：一个是帕累托劣均衡（A,M），即（“不信任并不等待”，“只说不做”）；另一个是帕累托最优均衡（B，N），即（“信任并等待”，“说到并做到”），在2b1+b2＞b3＞b1+b2+b4条件下成立。

演化博弈理论隐含了博弈双方有限理性程度均等的假设，因此，在面临多重Nash均衡时，与完全理性的博弈参与者类似，理性程度均等的博弈方同样难以做出协调一致的反应。为解决这一问题，米尔格朗和罗伯茨[7]提出了承诺偏好的假设，即博弈各方不管特定的均衡是什么，都只采取某一特定的战略；刘德海[8]提出：只有打破博弈双方理性水平的均等性假设，在完全理性的博弈方通过锁定具有帕累托最优的Nash均衡策略带引下，有限理性的对方在不断试错的重复博弈过程中才能最终收敛于具有帕累托最优的Nash均衡，双方也才有可能走出多重Nash均衡选择的困境。

与典型的演化博弈问题有所不同，住房保障政策的非对称博弈是一类一对多的非对称博弈，具有斯坦克尔伯格博弈特征。第一，政府（个体参与者）拥有更多的博弈信息，更为了解博弈结构和博弈策略，因而能够决策更为理性，即“高理性的”、“老练的”，符合斯坦克尔伯格领导者的条件；第二，城市弱势群体（群体参与者）的信息和学习能力相对弱势，更容易采取“短视的”、“幼稚的”低理性策略[9,10]。作为斯坦克尔伯格追随者在重复博弈中通过学习、试错可逐步达到最优策略。

因此，可以进一步假设在博弈的初始状态，城市弱势群体内部分别采取A策略（不信任并不等待）和“B”策略（信任并等待）的比例分布为θ(A)=x，θ(B)=(1-x)。

在重复博弈中，如果“高理性的”政府，作为博弈中的斯坦克尔伯格领导者，坚持以住房保障政策的长期收益为重，始终选择并锁定“有远见的”N策略（说并做），那么他的 长 期 收 益 可 以 用u(SN)= ∑t[(b3-b2)θt(B)+(b3-b2-b1)θt(A)]δt表示，其中，δ为政府未来阶段收益的贴现因子，其意义为政府是否具有“远见的”，并比较注重未来阶段 的 收 益 ，t为 重 复 博 弈 次 数 ，θt(A)∈(0,1)，θt(B)=1-θt(A)。随着t→∞，此时δt→1，θt(A)→0。在重复博弈中，“短视的”、“幼稚的”群体参与者通过学习与试错最终明白政府的N策略选择，并逐步全面采取相应最优的反应策略B（信任并等待），即θt(B)→1，城市弱势群体的长期收益将跃升到a2-a1＋a3，同时政府的长期收益u(SN)趋近b3-b2，从而实现帕累托最优的稳定Nash均衡（B，N）。

在重复博弈中，如果“高理性的”、“老练的”政府采取欺骗策略，可以实现更大的当期收益。即在博弈的最初阶段政府选择N策略，当“短视的”、“幼稚的”群体参与者逐渐收敛于B策略后，再将N策略转换为M策略，这样，政府通过误导城市弱势群体使博弈暂时收敛于帕累托最优的收益（a2-a1+a3，b3-b2），然后转换到策略M，这样就获得了几乎全部的群体参与者停留在B策略所造成的当期收益， 其 中θt(B)≈1 ，θt(A)≈0。显然，政府在先（B，N）然后（B，M）的收益大于在Nash均衡（A，M）中的收益。

3 结语

在住房保障政策的非对称博弈问题上，政府主要有“只说不做”与“说并做”二种博弈策略，城市弱势群体可以采用的二种主要博弈策略是“信任并等待”与“不信任并不等待”保障性住房。如果政府（斯坦克尔伯格领导者）能够选择并锁定“有远见的”“说并做”策略时，在重复博弈的过程中，作为斯坦克尔伯格追随者的城市弱势群体通过学习与试错，将会逐步摒弃“短视的”策略，全面采取相应的最优策略，从而解决多重Nash均衡精炼问题，实现住房保障政策的社会最优均衡。但是，为实现当期收益最大化，“高理性的”、“老练的”政府还存在着采取欺骗性策略的可能。依据本文提出的非对称博弈模型，政府在制定实施住房保障政策时，应重点关注以下几个方面：要充分发挥政府的信息与资源优势，坚持高理性；要以社会经济发展的长期收益为重，避免决策的短期行为（即b3＞b1+b2+b4）；珍视政府信用，住房保障政策要“说到并做到”，降低对b4的期望值；要加强住房保障政策的宣传，随着住房保障的社会意识逐步深入人心，a3、b3会不断增加，a4与b2也将同步下降，从而将有效减少住房保障政策的执行成本，即降低了y**和x**，帕累托均衡收益也将提升至（a2－a1＋a3,b3－b2）。同时，对于城市弱势群体来说应做到：密切关注政治、经济和社会等各方面的动态信息，不断提升自身的理性水平；顺应国家住房保障政策的导向，准确把握租购时机，既充分享受住房保障政策的优惠a2，又尽量避免非理性行为，减少a4的发生。

[1]张建坤,王效容等.“蚁族”保障性住房的PPP模式设计[J].东南大学学报（哲学社会科学版）,2012,(2).

[2]黄安永,朱新贵.我国保障性住房管理机制的研究与分析[J].现代城市研究,2010,(10).

[3]李新保障房的定位和融资[J].中国房地产金融,2012,(4).

[4]谢识予.经济博弈论[M].上海：复旦大学出版社,2006.

[5]Selten,R.Evolutionary Stability in Extensive Two-person Games[J].Math.Soc.Sc,1983,（5）.

[6]张良桥.进化稳定均衡与纳什均衡[J].经济科学,2001,(3).

[7]Milgrom,P.,J Roberts.Predation,Reputation and Entry Deterrence[J].Econometrica,1992,(50).

[8]刘德海,徐寅峰等.个体与群体之间的一类博弈问题分析[J].系统工程,2004,(12).

[9]徐江,刘应宗等.建筑节能激励政策的非对称博弈分析[J].电子科技大学学报(社科版),2006,(3).

[10]Basu,K.Stackelberg Equilibrium in Oligopoly：an Explanation Based on Managerial Incentives[J].Economics Letters,1996,(49).