基于支持向量机与相关向量机的高光谱图像分类

齐 滨，赵春晖，王玉磊

(哈尔滨工程大学信息与通信工程学院，哈尔滨150001)

20世纪80年代初，在多光谱遥感技术基础上出现了高光谱遥感技术，通过成像光谱仪记录带有地物光谱信息的太阳辐射信号，在可见光、近红外、短波红外、中红外等电磁波谱范围内利用狭窄的光谱间隔成像，获取近似连续、反映地物属性的光谱特征曲线;将表征地物属性特征的光谱信息与表征地物几何位置关系的空间信息有机地结合在一起，使地物的精确定量分析与细节提取成为可能。随着遥感图像处理技术的不断发展，高光谱遥感图像的光谱分辨率不断提升，与传统的多光谱遥感相比，高光谱图像提供的地物光谱信息更加丰富，使其无论在描述地物细节方面还是鉴别地物类别方面都有大幅度的提高，为地物精确分类的实现提供了有利的保障［1］，高光谱遥感的发展得益于光谱成像技术的逐渐成熟。光谱成像技术是集信号检测技术、探测器技术、精密光学技术和计算机信号处理技术于一体的综合性技术，其最大特点是将二维成像技术与光谱探测技术相结合，在对目标地物的空间特征进行成像的同时，对每个空间像元经过色散形成几百乃至几千个窄波段，进行近似连续的光谱波段覆盖，这样获得图像的每个像元将包含多个光谱特征。因此形成的高光谱数据可以用三维“数据立方体”形象地描述，其中二维表征地物的空间位置特征，另外一维表征地物的光谱波段特征［2］。

高光谱图像分类被定义为根据高光谱图像的光谱特征，对图像像素进行划分，将具有相似特征属性的像素划分为同一类，是高光谱图像处理的重要研究内容之一［3］。支持向量机是建立在结构风险最小化准则和VC维理论基础上，根据统计学理论，在有限的训练样本信息下，通过权衡经验风险与置信风险，在机器学习模型复杂度与机器学习方法能力之间寻求最佳折衷，在解决小样本、非线性以及高维模式识别中表现出特有的优势，具有较好的泛化能力［4］。相关向量机是在贝叶斯框架基础上提出的一种稀疏机器学习模型［5］，与支持向量机相比，相关向量机不受梅西定理的限制，可以构建任意的核函数，不需要设置惩罚因子，不仅获得二值输出，而且获得具有统计意义预测概率的结果输出。由于RVM引入了超参数向量，使得RVM更加稀疏，极大地减少了核函数的计算量，使得测试时间更短，具有更强的泛化能力［6］。由于支持向量机和相关向量机在处理高维数据分类时具有较高的分类精度，为此本文通过对支持向量机与相关向量机的理论对比分析，将这两种机器学习算法应用于高光谱图像分类中。实验结果表明，这两种机器学习算法均能较好地处理高光谱图像中存在的非线性特性，相比之下，支持向量机的总体分类精度要略高于相关向量机。

1 支持向量机分类器

支持向量机的基本思想是寻求一个最优分类超平面，使原数据中的两类样本可以被尽可能的分开，并且这两类样本间具有尽可能大的距离［7－8］，如图1所示。

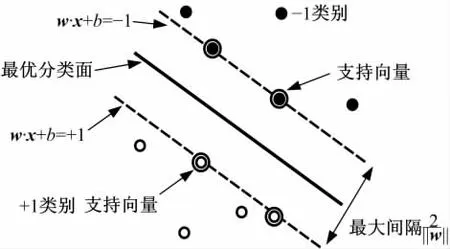
图1 具有最大间隔的最优分类超平面Fig.1 Optimal classification hyperplane with maximal margin

训练样本集{(x1，y1)，…，(xn，yn)}∈(RN，Y)，yi∈Y={－1，1}，i=1，2，…，n，支持向量机的目的为寻找最优分类超平面(w·x)+b=0的参数w和b，使得标号为+1和-1的样本点分别位于分类面的两侧。设标号为+1或-1的样本点中，通过距最优分类面距离最近且与最优分类面平行的两个平面为

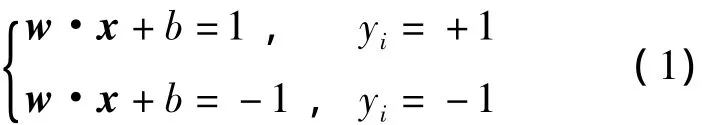
两个平面间的距离为

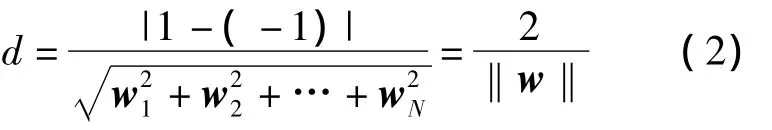
因此支持向量机的最优化问题转变为对下式权值向量w和参量b的求解

对于一般分类问题，由于存在线性不可分情况，为此引入松弛变量ξi，原凸二次规划问题变为

式中:ξ=(ξ1，ξ2，…，ξn);C＞0为惩罚参数。引入拉格朗日乘子αi和βi，式(4)求解方程为

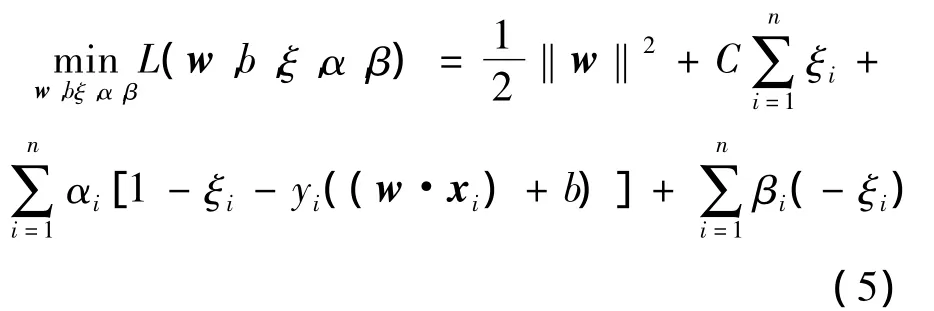
对w，b，ξi分别求偏导得

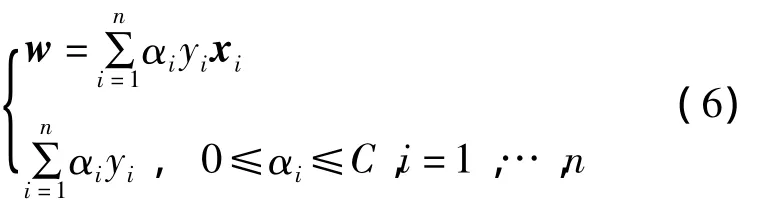
将式(6)代入式(5)中得到关于α的函数

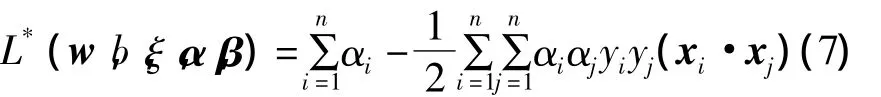
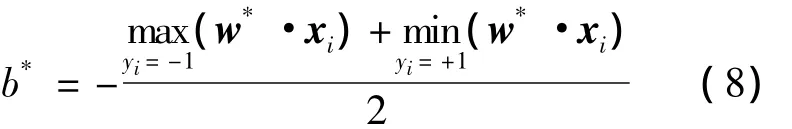
对于高维空间，如果用内积K(x，x')代替最优分类面中的点积(x·x')，求解上述问题后，得到的支持向量机判别函数为

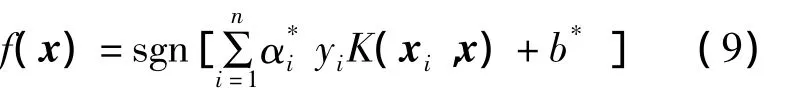
式中:

2 相关向量机

2.1 贝叶斯模型

对于两类分类问题，假定训练样本集为{xn，tn，xn∈Rd为训练样本，tn∈{0，1}为训练样本标号，ti为预测样本标号，ti=yi+εi，其中:w0为分类预测模型;εi为均值为0，方差为σ2附加噪声，εi～N(0，σ2)，ti～N(yi，σ2)。假设训练样本集独立同分布，观测结果向量t服从下式分布

RVM通过样本标号t预测测试样本标号t*

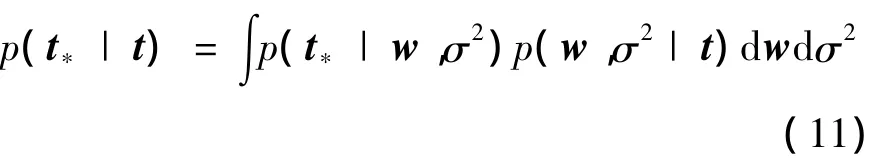
为使权值向量w的大部分分量为0，减少核函数的计算量，为权值向量w添加附加条件。设wi服从均值为0，方差为 α－1i的分布wi～ N(0，)

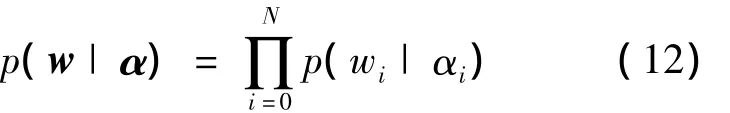
式中:α为权值向量w先验分布的超参数向量。

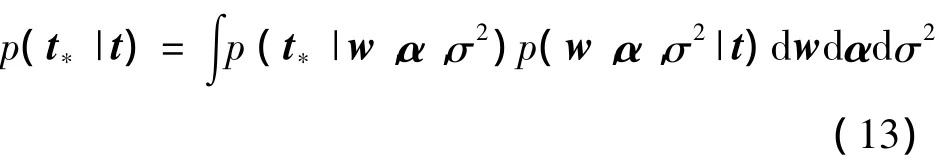
式中:p(t*|w，α，σ2)=N(t*|y(x*;w)，σ2)。

2.2 模型参数估计

由于p(w，α，σ2|t)不能通过积分获得，故利用贝叶斯公式将其分解

对p(t|w，σ2)和p(w|α)的乘积的积分得

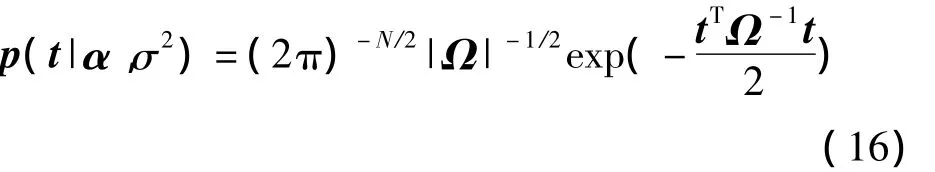
式中:Ω=σ2I+ΦA－1ΦT，A=diag(α0，α1，…，αN)

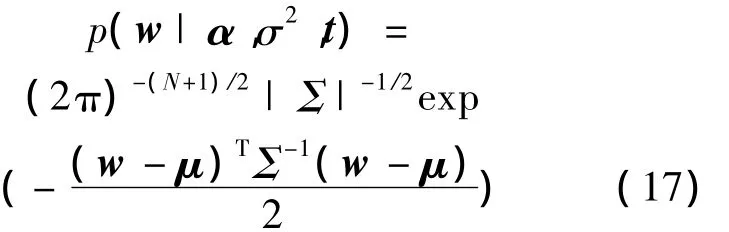
式中:Σ=(σ－2ΦTΦ+A)－1，μ=σ－2ΣΦTt。

由于p(α，σ2|t)∝p(t|α，σ2)p(α)p(σ2)，因p(α，σ2|t)无法积分求解，使用最大似然函数法近似替代p(α，σ2|t)，即

αMP和的迭代求解过程如下所示

式中:Σi，i是Σ中第i项对角线上的元素，对于给定的初始α与σ2初值，通过式(19)的不断更新，获得逼近的αMP和。足够多次更新后，大部分的αi会接近无限大，与之对应的wi为0，其他αi接近有限值，此时对应的xi称之为相关向量。

2.3 相关向量机分类

对于二分类问题，目标值{ti只能为0或1，我们采用S形函数对非线性基函数映射，进行类别判定

若每次观测都为独立事件，得到观测结果为

对于权值w，使用最大似然法对其求解

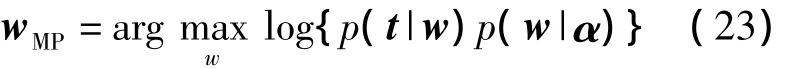
3 实验结果与分析

为验证SVM和 RVM的分类性能，使用AVIRIS高光谱数据对这两种算法进行验证。高光谱图像拍摄于1992年6月，图像为美国印第安纳州印第安农林实验区的一部分，如图2所示。图像大小为144×144，共220个波段，去除一些受噪声影响较大的波段，从原始的220波段中选取200个波段作为研究对象。实验选取9类样本像素点个数较多的地物对SVM和RVM的分类性能进行比较，主要包括:玉米1、玉米2、牧场、灌木、干草、大豆1、大豆2、大豆3和乔木。训练样本与测试样本如表1所示。

图2 AVIRIS高光谱图像Fig.2 AVIRIS hyperspectral imagery

表1 训练样本与测试样本Table 1 Training sam p les and testing sam p les

为便于比较，支持向量机和相关向量机均采用高斯径向核函数，由于支持向量机含有规则化系数C，在分类时需要设置，因此使用交叉验证网格搜索法来获取。对于本实验所使用的AVIRIS数据，获取得到的规则化系数C=181.02，高斯径向核函数的参数γ=1.41。为便于与支持向量机比较，相关向量机的核函数参数设置与支持向量机相同。支持向量机和相关向量机的分类结果如图3所示，各类分类精度与总体分类精度如表2所示。

表2 SVM和RVM的分类精度Table 2 Classification accuracy of SVM and RVM

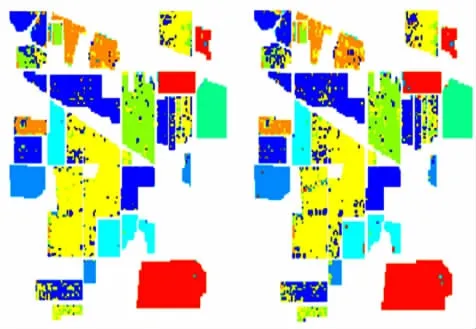
图3 AVIRIS数据的分类结果Fig.3 Classification results of AVIRIS data

从表2中可以看出，相对于玉米1、玉米2、大豆1、大豆2和大豆3等5种地物，牧场、灌木、干草和乔木等4种地物的各类分类精度较高。与相关向量机相比，支持向量机的总体分类精度略高。

4 结束语

本文介绍了支持向量机和相关向量机的理论基础、基本原理和算法的实现。支持向量机是建立在结构风险最小化准则和VC维理论基础上，依据统计学理论，在训练样本信息有限的情况下，在机器学习模型复杂度与机器学习能力之间寻求最佳折衷，很大程度上克服了传统机器学习中的维数灾难和局部极小等问题。核函数的引入使得支持向量机在解决非线性数据处理和高维数据模式识别中表现出显著的优势。相关向量机的训练是在贝叶斯框架下进行的，在先验参数的结构下基于主动相关决策理论移除不相关的点，从而获得稀疏化的模型。在样本数据的迭代学习过程中，大部分参数的后验分布趋于零，非零参数所对应的学习样本，与决策域的样本并不相关，因此这些样本体现了数据中最核心的特征。与支持向量机相比，相关向量机没有规则化系数，核函数不受梅西定理的限制，可以构建任意的核函数，不需要对惩罚因子做出设置，不仅获得二值输出，还可以获得具有统计意义的概率输出，但在训练时间上，相关向量机要比支持向量机长。支持向量机和相关向量机对非线性问题和不可分问题的处理技巧体现了这两种机器学习算法的独特优势。

［1］Li J，Bioucas JM，Plaza A.Spectral－spatial hyperspectral image segmentation using subspace multinomial logistic regression and markov random fields［J］.IEEE Transanctions on Geoscience and Remote Sensing，2012，50(3):809－823.

［2］Zhang L，Zhang L，Tao D.On combining multiple features for hyperspectral remote sensing image classification［J］.IEEE Transanctions on Geoscience and Remote Sensing，2012，50(3):879－893.

［3］Zhong Y，Zhang L.An adaptive artificial immune network for supervised classification ofmulti－/hyperspectral remote sensing imagery［J］.IEEE Transactions on Geoscience and Remote Sensing，2012，50(3):894－909.

［4］Lin K P，Chen M S.On the design and analysis of the privacy－preserving SVM classifier［J］.IEEE Transanctions on Knowledge and Data Engineering，2011，23 (11):1704－1717.

［5］Mianji F A，Zhang Y.Robust hyperspectral classification using relevance vectormachine［J］.IEEE Transanctions on Geoscience and Remote Sensing，2011，49(6):2100－2112.

［6］Wei L，Yang Y，Nishikawa R M.Relevance vector machine for automatic detection of clusteredmicrocalcifications［J］.IEEE Transanctions on Medical Imaging，2005，24(10):1278－1285.

［7］Tarabalka Y，Fauvel M，Chanussot J.SVM－and MRF－based method for accurate classification of hyperspectral images［J］.IEEE Geoscience and Remote Sensing Letters，2010，7(4):736－740.

［8］Pal M，Foody G M.Feature selection for classification of hyperspectral data by SVM［J］.IEEE Transactions on Geoscience and Remote Sensing，2010，48(5):2297－2307.