应用PCA理论进行多人脸姿态估计的方法

宋怀波，史建强，2

(1.西北农林科技大学机械与电子工程学院，陕西杨凌712100;2.西安交通大学机械工程学院，西安710049)

人脸姿态识别通过确定二维图像中的人脸在三维空间中的姿态，近似地计算人脸对应于三维空间坐标轴的偏转角度［1］。人脸姿态识别是多姿态人脸识别的关键步骤，只有确定了人脸姿态信息，才能实现对人脸姿态的正确识别。人脸姿态识别在人机交互［2］、智能监控［3］、虚拟现实［4］和司机疲劳检测系统［5］等方面有着广泛的应用。

人脸姿态识别的方法大致分为基于模型的方法和基于人脸特征的方法两类［6］。基于模型的方法［7－8］通过建立人脸与几何模型的对应关系，提取人脸的某些特征，利用已知几何模型实现人脸姿态的识别。这种方法的准确率和效率较高，但由于姿态的多样性，二维与三维特征点之间的几何对应关系建立比较困难;基于人脸特征的方法［9－10］假设人脸姿态和人脸图像的某些特征间存在某种对应关系，通过建立人脸姿态与这些特征的对应关系进行人脸姿态的识别。为确定这些关系，需要对大量不同姿态的人脸图像通过统计方法建立特定的对应关系。这种算法简单，由于以整个人脸图像作为研究对象，对人脸图像的考虑更细致，对表情、光照等条件的影响鲁棒性更强，但由于需要建立大量训练样本，其计算量一般较大。

本文提出了一种基于PCA算法的人脸姿态识别方法，即利用大量的图像样本得到人脸姿态和人脸图像在特征空间投影之间特定的对应关系。使数据可在一个低维的空间进行处理，同时保持了原始数据的绝大部分有效信息，从而解决了人脸特征方法中数据空间维数过高的问题，降低了运算量也提高了运算速度，而且该方法的准确率和效率也较高。

1 PCA原理

PCA作为一种降维方法，将高维空间上的数据投影到低维子空间中，并使得在最小二乘意义下的低维表示能够更好的描述高维空间上的原始数据［11－12］。如设已知变量X为k维，欲将维数压缩为g(g＜k)，需求得输入向量的相关矩阵的特征值和特征向量，并对其特征值由小到大进行排列，将保留大部分能量信息的g个特征值对应的特征向量构成特征子空间。

1.1 SVD基本理论

由于图像的维数较高，在求解特征值和特征向量时，其求解过程比较耗时，一般采用奇异分解方法实现［13］。其基本原理为:设A是秩为P的N ×P维矩阵，则存在两个正交矩阵

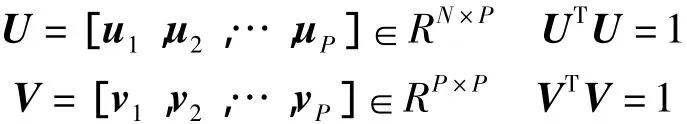
已知对角矩阵

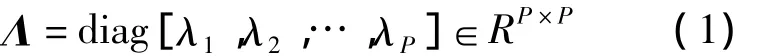
且λ1≥λ2≥…，≥λP，使得

式中:λi(i=1，2，…，P)为矩阵AAT和ATA的非零特征值，ui、vi分别是AAT和ATA对应的正交归一特征向量。

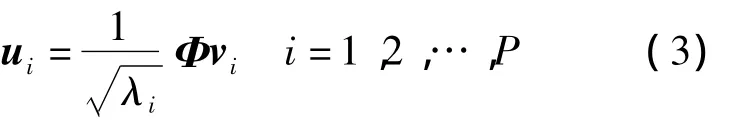
式中:ui(i=1，2，…，P)即为求得的特征向量。

1.2 特征子空间的创建

对于一幅m×n大小的样本图像，按列排列构成一个m×n维的列向量，即:X=［x1，x2，…，xm×n］T，则对于同一类样本中的N个样本图像集合可用矩阵［X1，X2，…，XN］表示，设这N张样本图像的均值为μ，对集合中的样本进行处理，将各样本减去μ，计算离散差值，组成矩阵

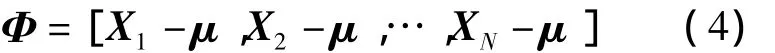
X的协方差矩阵

特征值等式如下

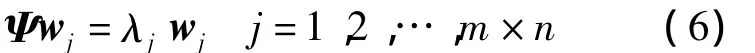
通过式(6)可求出矩阵Ψ的特征值λj和特征向量wj。将特征值由大到小的顺序进行排序，则对应的特征向量组成的矩阵为

至此，m×n维特征子空间构造完成。

2 基于PCA的人脸姿态估计

2.1 多人脸姿态估计流程

研究表明，人脸图像处于一个低维线性空间中，且不同姿态的人脸在该低维线性空间具有可分性，其重点是找到该低维线性空间。在PCA方法中，通过对读入的人脸图像进行训练，得到各自类别的特征子空间来进行处理。在完成该步骤后，即可将测试样本分别向训练好的各个子空间进行投影，根据其在子空间内投影距离的大小进行姿态的估计。

2.2 人脸姿态数据库的创建

人脸姿态数据库由23类共690个样本组成，每类姿态 30个样本，部分样本来自 http:// download.csdn.net/down/2591527/tinypeter。所有样本均归一化为32×24大小。多姿态人脸样本库在竖直方向有平视、仰视30°、仰视60°、俯视30°、俯视60°五种姿态类型。各类中还包括水平方向旋转不同角度的类型，其中平视类中各有直视0°、左右旋转30°、左右旋转60°和左右旋转90°七类姿态，仰视30°、仰视60°类中各有直视0°、左右旋转45°和左右旋转90°五类姿态，俯视30°、俯视60°类中各有直视0°和左右旋转45°三类姿态。图1给出了仰视30°向右旋转45°及左旋转90°姿态的示例。

图1 仰视30°向右旋转45°及左旋转90°姿态库中的人脸Fig.1 faces of looking up at 30 degrees，rotating right 45 degrees，rotating left 45 degrees in poses atlas

2.3 姿态子空间维数的确定方法

应用PCA理论进行姿态估计的关键是寻求各类别样本集的子空间维数，目前还没有一个通用的计算方法。为了保证获取足够多的信息而又不会使信息丢失过多，本文采用计算信息量的方法求取子空间的维数［14］

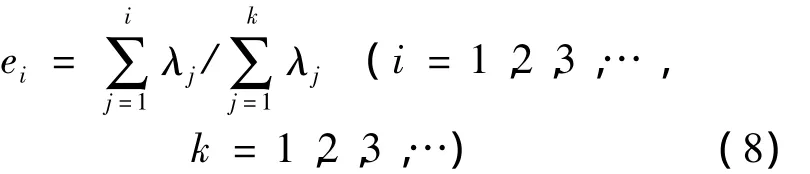
这种子空间维数确定方法有效地保持了训练样本集的主要信息，而又使得其始终处于一个较低的线性维数之中，便于信息的快速处理。在姿态估计阶段，将待测样本按下式投影到各子空间

通过计算测试样本在该空间内的投影大小即可获得其姿态估计的结果，其分类方法按2.4节处理。

2.4 分类识别

经过特征提取后，测试样本最终成为特征空间中的一个点，通过计算距离或角度即可实现姿态的识别。采用欧式距离测度进行姿态分类的公式如下

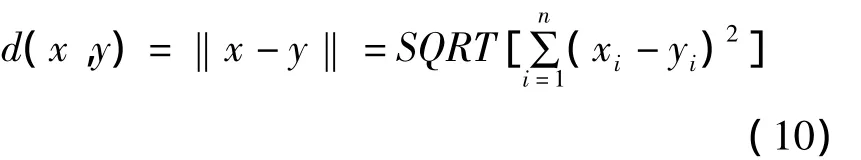
式中:x，y为n维特征空间的两个点。分别计算测试样本在各子空间中的投影距离并选择距离最小的一类子空间即可实现其姿态的估计工作。

3 实验结果分析

3.1 测试样本的选择

为了验证本方法的有效性，在每一类姿态样本中随即选择30个样本进行训练，并选取75张不同于训练样本的不同姿态的样本进行测试。部分样本示例如图2所示。

图2 部分测试样本图像Fig.2 Partial testing samples

3.2 实验结果及讨论

为了验证姿态子空间维数对识别结果的影响，在式(8)中，分别选取不同的截取阈值进行处理，已得到不同的子空间维数，不同子空间维数下的姿态估计结果如图3所示。

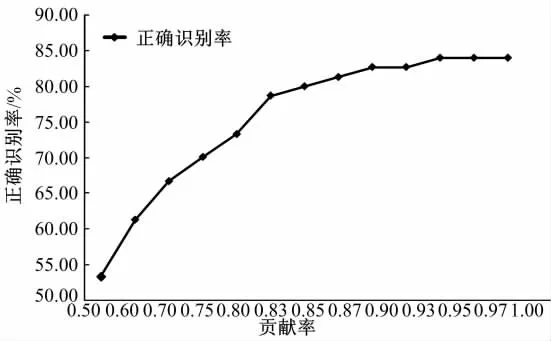
图3 不同的贡献率对于其识别率曲线图Fig.3 Estimation rate by choosing different subspace dimensions

由图3可以明显发现，随着方差贡献率的增大，姿态估计准确率也稳步提高。同时可以看出，在贡献率较小时，微小的变换也会造成姿态估计结果的显著变化，如贡献率从0.5增加到0.6，识别率提高了近10%。之后随着方差贡献率的进一步增加，姿态估计准确率也随之提高并趋于平稳。当贡献率达到0.95后，人脸姿态的正确估计率基本趋于稳定。

4 结束语

利用PCA算法所具有的计算方法简单和计算效率高的特点，将其应用于多人脸姿态估计中。实验结果表明，该方法的最高姿态估计准确率可达84%;方差贡献率对识别结果具有较大影响，方差贡献率越大则姿态估计正确率越高，但当贡献率达到一定值时，姿态估计准确率将趋于稳定。

不足之处在于，文中采取能量信息截取的方法来选取子空间维数，未能实现最优子空间维数的选取，如何去除无效的特征向量以及如何选取最优的子空间维数是下一步研究的重点。

［1］JiQiang，Hu Rong.3D face pose estimation and tracking from amonocular camera［J］.Image and Vision Computing，2002，20(7):499－511.

［2］薛雨丽，毛峡，郭叶，等.人脸交互中的人脸表情识别研究进展［J］.中国图象图形学报，2009，14(5):764－772.

Xue Yu－li，Mao Xia，Guo Ye，et al.The research advance of facial expression recognition in human computer interaction［J］.Journal of image and graphics，2009，14(5):746－772.

［3］宋红，石峰.基于人脸检测与跟踪的智能监控系统［J］.北京理工大学学报，2004，24(11):966－970.

Song H，Shi F.Face detection and tracking for intelligent surveillance system［J］.Journal of Beijing Institute of Technology，2004，24(11):966－970.

［4］李旭东.用于人脸表情图像与动画合成的图像变形方法［J］.武汉大学学报信息科学版，2007，32(9): 796－799.

Li Xu－dong.Image morphing method for facial expression image and animation synthesis［J］.Journal of Geomatics and Information Science of Wuhan University，2007，32(9):796－799.

［5］李志春.驾驶员疲劳状态检测技术研究与工程实现［D］.镇江:江苏大学，2009.

Li Zhi－chun.Research on driver’s fatigue status detection technology and realization in engineering［D］. Zhenjiang:Jiangsu University，2009.

［6］Yun Fu，Thomas Huang.Graph embedded analysis for head pose estimation［C］//7th International Conference on Automatic Face and Gesture Recognition，2006:3－8.

［7］刘金葵.正面人脸判别的方法研究［D］.广州:中山大学，2009.

Liu Jin－kui.The research of the positive face discrimination［D］.Guangzhou:Central South University，2009.

［8］孙昊翔.关于人脸姿态估计方法的研究［D］.长春:吉林大学，2007.

Sun Hao－xiang.The research of the face pose estimation［D］.Changchun:Jilin University，2007.

［9］Chen Q，Wu H，Shimada T.A robust algorithm for 3D head pose estimation［C］//International Conference on Multimedia Computing and Systems，Nara，1999:697－702.

［10］Hu Y X，Chen L B，Zhou Y，et a1.Estimating face pose by facial asymmetry and geometry［C］//IEEEConf.on FG’04，2004:651－656.

［11］Hu F，Wang Y，Wu H.Mobile telemedicine sensor networks with low－energy data query and network lifetime considerations［J］.Mobile Computing，2007，5(4): 404－417.

［12］张媛，张燕平.一种PCA算法及其应用［J］.微机发展.2005，15(2):69－72.

Zhang Yuan，Zhang Yan－ping.An algorithm of PCA and its application［J］.Microcomputer Development，2005，15(2):69－72.

［13］王宏拥，廖海斌，段新华，等.基于奇异值与特征融合矩阵的自适应人脸识别［J］.计算机工程与应用，2010，46(7):162－164.

Wang H Y，Liao H B，Duan X H，et al.Weighted adaptive face recognition using singular value and featurematrix［J］.Computer Engineering and Applications，2010，46(7):162－164.

［14］孙即祥.现代模式识别［M］.北京:国防科技大学出版社，2002.