基于光谱相似度量的高光谱图像异常检测算法

王玉磊，赵春晖，齐 滨

(哈尔滨工程大学信息与通信工程学院，哈尔滨150001)

高光谱遥感图像具有很高的光谱分辨率，是一种图谱合一的新型遥感数据。借助其丰富的光谱信息，可以反映目标间的细微差异，使人们能够发现许多在常规遥感中无法或难以探测的地面目标，这为目标检测提供了有利的支持，因而越来越受到人们的重视。异常检测是高光谱图像处理的一个重要分支，它能够在没有先验光谱信息的情况下检测到与周围环境存在光谱差异的目标，在军事防御、农业、地质探测、医疗诊断以及环境监控等方面都有重要的应用，成为了高光谱目标检测领域的一个研究热点。从已有文献中可知，异常目标具有以下特性:(1)它是unexpected;(2)与背景相比，它的样本空间非常小;(3)它的发生概率非常低;(4)异常目标与周围背景的光谱信息有很大的区别。

文献［1］提出了一种基于广义似然比检测(GLRT)的异常算子，并称之为RX异常算子。目前RX算子及其改进模型已成功应用于高光谱图像异常探测［2－6］，并已成为高光谱异常检测的一个基准算法。该算法是一种局部异常检测算法，用于在高斯背景统计特性和空间白化的条件下检测空间模式己知而光谱特性未知的目标物，其渐进意义下的检测器将原始算法简化为求待检测点到周围背景均值的马氏距离。RX算法是在一些简化的假设条件下构造的似然比检测算子，直接利用RX算法对高光谱图像进行处理将会产生较高的虚警概率。这主要是由两方面原因造成的: (1)RX算法中所采用的局部统计模型假定数据是空间不相关的，或者是空间白化的，且数据要求服从局部正态分布，然而，由于实际地物分布是复杂多变的，这种假设不能全面地描述真实场景的情况;(2)当RX算法直接用于高光谱图像处理时，需要计算样本的协方差矩阵及其逆矩阵，而协方差矩阵的维数会随着波段数目的增加而迅速增加，这将会带来巨大的计算量。

近年来，随着统计学习理论的快速发展和逐步完善，应用核机器学习算法对高光谱图像进行处理成为可能。将高光谱数据映射到高维的特征空间进行处理，充分挖掘其隐含的非线性信息，进一步提高高光谱小目标与背景之间的分离性能。目前已有学者Kwon对传统高光谱小目标检测算法，RX算子进行了改进［2］，利用核函数将原始空间光谱信号映射到高维特征空间，进而实现了小目标的异常检测;通过与传统高光谱小目标检测算法检测性能的比较，得出核算法在提高目标检测概率和降低虚警方面有显著提高，然而该算法仍然是基于RX的基本假设基础的前提下，并且仍然需要巨大的计算量。

为了去除对背景模型的假设以及提高异常检测算法的实时性，本文提出了一种新型无假设模型的快速异常检测算法。首先讨论了光谱相似度量的方法及其效果，选用光谱角余弦作为光谱相似度量准则;然后从端元提取入手，采用迭代误差分析方法(IEA)对高光谱数据进行异常端元提取;最后采用核函数方法，利用得到的异常端元作为参考数据，以核光谱角余弦(KSAC)作为相似度量准则，对所有像素点进行判别，得到异常检测结果。

1 光谱相似度量

很多光谱图像处理算法都是基于光谱相似或者光谱距离的，从而估计两个光谱向量的相似程度。

欧氏距离是传统的基于几何学的向量距离，其计算公式如下

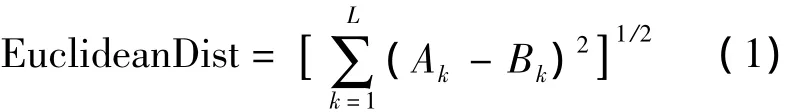
欧氏距离是向量距离最简单的计算方法，但是却不是精确的方法。

图1和图2分别给出了两组模拟数据。图1给出了两个弱相关的向量(r2≈0.000 6)，而图2则给出了两个强正相关的向量(r2≈0.999 3)。

通过式(1)计算两组数据的欧氏距离均为0.481 18。若以欧氏距离作为相似度标准，两组数据的欧氏距离相同，应得到相同的判别结果。然而，从图1和图2中很明显可以看出，第一组数据是弱相关甚至不相关的，而第二组数据具有强相关性。因此欧氏距离并不能很好地反应向量的相似程度。

图1 两个弱相关向量(欧氏距离为0.481 18)Fig.1 Two weakly correlated vectors

图2 两个强正相关向量(欧氏距离为0.481 18)Fig.2 Two strong positive correlated vectors

光谱角余弦(Spectral Angel Cosine，SAC)是一种计算光谱相似度的方法［7］，它同时反映了光谱向量在数值上的差异和光谱曲线之间、形状之间的差异。相比马氏距离，用光谱角余弦作为光谱相似度测量具有明显的优点。光谱角余弦的计算公式如下

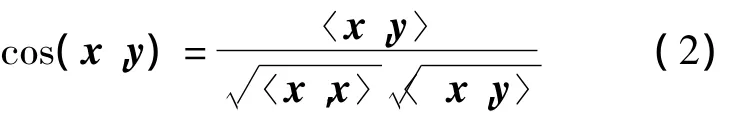
式中:x和y为像元的光谱向量;〈·，·〉为内积运算。光谱角作为两个光谱向量的夹角，光谱角越小，两个光谱向量的相似度就越高，SAC就越接近1。

同样以图1和图2两组模拟数据为例，以光谱角度作为光谱相似度量的标准，计算两组数据的相似程度。图1通过式(2)计算得两个光谱向量的光谱角为32.662 6°;而图2通过式(2)计算得两个光谱向量的光谱角为3.799 2°。两组数据得到的光谱角度差异较大，通过设定适当的角度阈值，图1两个光谱向量可认为是不相似的，而图2两个光谱向量可认为是相似的，用此标准得到的结果是比较符合实际情况的。

2 基于光谱相似度量的异常检测算法

2.1 端元提取算法

光谱相似度量方法需要有特定的参考光谱向量，在此可用端元提取的方法来获得。

高光谱数据端元提取是理解高光谱数据，进而对高光谱数据进行下一步处理(如混合像元分解、分类、地物识别)的重要前提。目前，高光谱数据端元提取的主要方法有纯像元指数法(Pure Pixel Index，PPI)、N－FINDR、迭代误差分析法(Iterative Error Analysis，IEA)、顶点成分分析(Vertex Component Analysis，VCA)、最大距离法单行体体积法等［8－10］。在此选用了迭代误差分析法对高光谱数据进行端元提取。

迭代误差分析(IEA)是一种不需要对原始数据降维或去冗余而直接对数据进行处理的端元提取方法。迭代误差分析是建立在线性混合模型的基础上，线性混合模型可表示为:

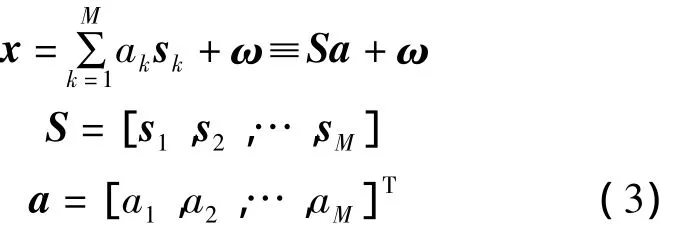
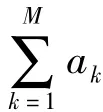
在式(1)中，假设端元矩阵S已知，则x的最小均方估计为:

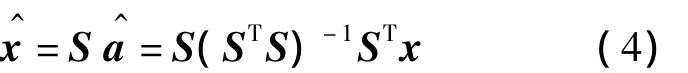
均方根误差表示为模长:

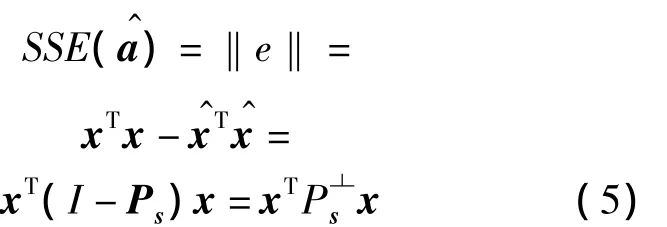
迭代误差分析算法的步骤如下:

首先，给定一个初始向量(一般为图像中所有光谱的均值向量)，用它来代替式(2)中的S;

第二，用得到的S计算均方根误差，对图像数据中每个向量通过式(3)求取均方根误差，得到一幅误差图像;

第三，选择误差图像中较大的点，并以此点为中心，以一定角度为门限，选择与此点角度较小的点进行平均，将得到的平均波谱作为第一个端元。

重复上面步骤，直至找到规定数量的端元或者均方根误差小于一个特定门限。

2.2 异常检测算法

在采用IEA算法获取异常端元后，就可用异常端元作为参考端元，对所有像元进行相似度量，从而实现异常检测。相似度量准则采用核光谱角余弦准则［11］。

光谱角余弦如式(2)所示，将原始输入数据空间通过非线性映射函数Φ映射到高维特征空间中，此时式(2)变为

由于特征空间的维数很高(甚至可能趋于无穷)，同时由于非线性映射函数未知，这使得直接在特征空间进行计算变得很困难甚至不可能实现。核函数方法可以将特征空间的点积转化为输入空间数据的核函数实现，从而巧妙地避开了在高维的特征空间计算点积。

核函数k(x，y)表示如下:

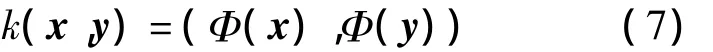
常用的核函数有高斯径向基核函数和多项式核函数，数学模型分别如下:

高斯径向基核函数:

多项式核函数:

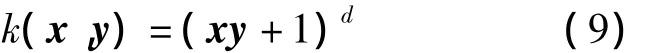
在此选用高斯径向基核函数(RBF)，这是因为当选用高斯径向基核函数时，若x=y，则有k(x，y)=1，因而式(6)的分母部分为1，可大大降低式(6)的复杂度。

将式(7)和式(8)代入式(6)并化简得KSAC的数学表达式为:

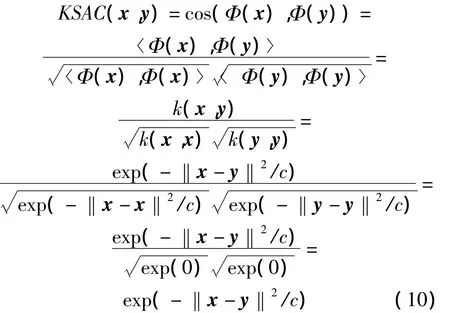
式中:x是待检测像元的光谱向量;y是参考像元的光谱向量，即端元光谱向量。

根据式(10)，将IEA算法获取的异常端元代入y，x为待检测像元，设定合适的阈值即能得到异常检测结果。算法流程如3所示。

图3 算法流程Fig.3 Algorithm flowchart

4 仿真实验与结果分析

为了验证算法的有效性，利用真实的高光谱图像进行仿真实验，实验中采用的高光谱图像数据是由AVIRIS传感器获取的美国圣地亚哥机场图像，如图4所示。该数据已经过大气校正和几何校正等预处理，是以反射率数据形式进行存储的，关于该高光谱图像数据的具体的参数如表1所示。

从原始图像中截取60×60的一段含有四个飞机目标的子图，图5为截取的高光谱子图的第一个波段示意图及地面目标分布。本文分别以光谱角余弦(IEA_SAC)与核光谱角余弦(IEA_ KSAC)作为光谱相似度量准则，设计了高光谱异常检测算法。

图4 高光谱图像数据源Fig.4 Hyperspectral data

表1 实验用高光谱图像数据源参数Table 1 The parameters of hyperspectral imagery for numerical experiment

图5 第1波段及地面目标分布图Fig.5 The 1st band and real target distribution

4.1 端元提取

实验中，在对高光谱数据进行归一化处理后，用IEA算法对高光谱数据进行端元提取。其中，IEA算法有两个重要的参数，即参与平均的波谱数目R和角度门限θ。参与平均的波谱数目R决定了所提取出的端元是背景端元还是异常端元，这是因为背景数目要远远多于异常点的数目。因此，在提取出的端元中，如果参与平均的波谱数目较多，一般为背景端元;反之，参与平均的波谱数目较少，应为异常端元。角度门限θ决定了光谱是否参与平均，一般来说，角度门限θ较小。

为了验证参数范围对算法鲁棒性的影响，我们讨论参与平均的波谱数目R和角度门限θ对端元提取的影响。实验中对IEA算法分别设置不同的参数进行端元提取，得到的结果如表2和表3所示。

表2 θ=8°时IEA算法中参与平均的波谱数目Table2 The average spectrum number in IEA at θ=8°

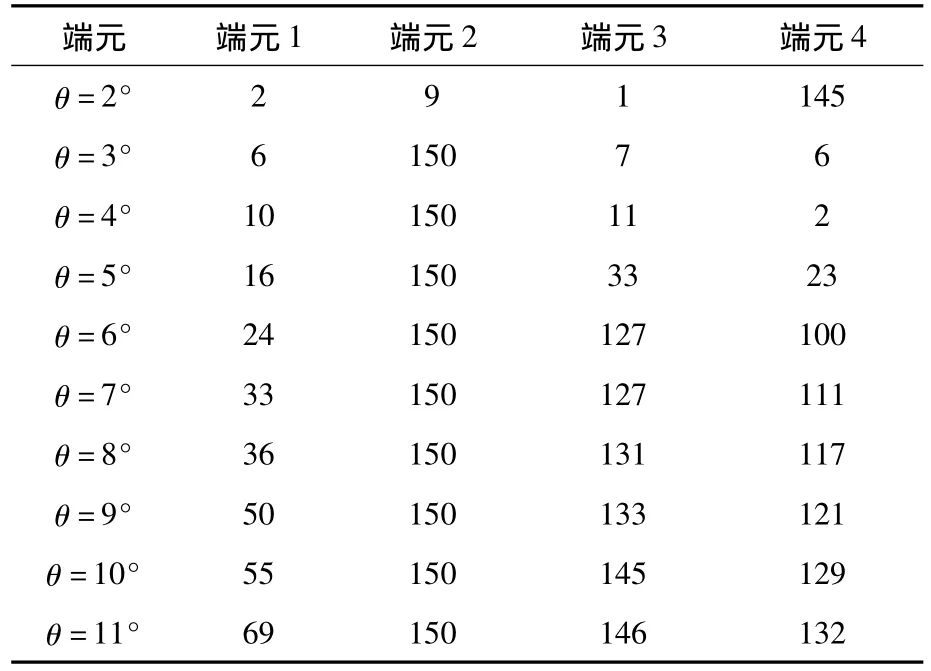
表3 R=150时IEA算法中参与平均的波谱数目Table3 The average spectrum number in IEA at R=150

通过表2可以看出，参与平均的像素数R对IEA算法没有太大影响。但是当R取值很小，各个端元参与平均的波谱数目比较接近，此时无法判断该端元是异常端元还是背景端元;当R到达一定值后，此参数对端元提取的结果就没有太大的影响。此时，为了节省计算量，应尽量选取较小的R值，故需根据与图像总像素数的比例选取合适的R值。由表3分析可得，当角度门限θ为2°～5°，由于角度过小，得到的结论并不完全准确。随着角度门限的增大，参与端元1平均的像素数始终较少，但是光谱之间的差异会随之增大，此时不能保证参与平均的像素均属于同一端元。因此，角度门限应尽量取较小值，但并不是越小越好。

本文中设置参数R=400，θ=8°，在IEA算法的每次循环中，由R和θ所确定的参与平均波谱的数目如表4所示。

表4 IEA算法中参与平均的波谱数目Table 4 The average spectrum number in IEA algorithm

从表4中可以看出，参与端元1平均的波谱数目只有36个，说明此端元为异常，即目标端元。

4.2 异常检测

将得到的目标端元作为参考端元，可以进行相似度量从而完成异常检测。首先采用式(2)的光谱角余弦表达式作为相似度量判别式，异常检测结果如图6所示，图6(a)为原始高光谱图像第一波段，图6(b)为IEA_SAC算法检测结果二值化图。

图6 IEA_SAC异常检测结果Fig.6 IEA_SAC anomaly detection result

采用式(10)的核光谱角余弦表达式作为相似度量判别式。检测结果如图7所示。其中图7 (a)为原始高光谱图像第一波段，图7(b)为IEA_ KSAC算法检测结果二值化图。

图7 IEA_KSAC异常检测结果Fig.7 IEA_KSAC anomaly detection result

IEA_SAC算法与IEA_KSAC算法的阈值取值区间如表5所示。阈值取值区间是指得到余弦最大值与最小值之间的差异。从表5中可以看出，KSAC的取值区间明显大于SAC取值区间，可明显降低算法对阈值选择的敏感度。同时，由于引入高斯径向基核函数对KSAC进行化简，从而无需多次计算内积，使式(10)的计算复杂度低于式(5)。从表2算法运行时间可以看出，KSAC算法的运行时间还不到SAC运行时间的一半，当数据量较大时，KSAC的效率要明显高于SAC。

表5 阈值取值区间与运行时间Table5 Threshold value interval and running time

从检测结果二值化图(见图7和图8)中可以看出，基于核光谱角余弦的异常检测算法的检测效果比较理想，飞机目标被很好地检测出来。同时，由于该算法没有大量的矩阵运算及内积运算，因此算法复杂度较低，运算速度快。

5 结束语

本文提出了一种新型的高光谱异常检测算法。该算法利用光谱相似度量的方法，通过计算当前像素点与参考异常端元的相似性进行异常判断。文中给出了基于高斯径向基的核光谱角余弦(KSAC)的定义及表达式，并设计了基于KSAC的高光谱图像异常检测算法。该方法适用于实际的高光谱图像异常检测，并具有检测效果好、算法复杂度低、运算速度快的特点。然而，核函数中参数优化是一个重要的研究方向，文中并没有给出核函数及参数的优化，因此在参数选择上径向基核函数的宽度是靠大量仿真实验比较得出的，没有实现自动选取，该项工作有待进一步进行研究。

［1］Irving S Reed，Yu Xiao－li.Adaptive multiple－band cfar detection of an optical pattern with unknown spectral distribution［J］.EEE Transactions on Acoustics Speech and Signal Processing，1990，38(10):1760－1769.

［2］Heesung K，Nasrabadi N M.Kernel RX－algorithm:A nonlinear anomaly detector for hyperspectral imagery［J］.IEEE Transactions on Geoscience and Remote Sensing，2005，43(2):388－397.

［3］梅锋，赵春晖.基于空域滤波的核RX高光谱图像异常检测算法［J］.哈尔滨工程大学学报，2009，30 (6):697－702.

Mei Feng，Zhao Chun－hui.Spatial filter based anomaly detection algorithm for hyperspectral imagery kernel RX detectors［J］.Journal of Harbin Engineering University，2009，30(6):697－702.

［4］Zhao Chun－hui，Wang Yu－lei，Mei Feng.Kernel ICA feature extraction for anomaly detection in hyperspectral imagery［J］.Chinese Journal of Electronics，2012，21 (2):265－269.

［5］赵春晖，胡春梅.基于目标正交子空间投影加权的高光谱图像异常检测算法［J］.吉林大学学报:工学版，2011，41(5):1468－1474.

Zhao Chun－hui，Hu Chun－mei.Weighted anomaly detection algorithm for hyperspectral image based on target orthogonal subspace projection［J］.Journal of Jilin U－niversity(Engineering and Technology Edition)，2011，41(5):1468－1474.

［6］王斯博，杨春玲.基于RX算法的高光谱红外弱小目标检测［J］.红外技术，2010，32(4)::204－208.

Wang Si－bo，Yang Chun－ling.Detection of dim small targetbased oil rx algorithm for hyperspectral ir imagery［J］.Infrared Technology，2010，32(4):204－208.

［7］James Norman Sweet.The spectral similarity scale and its application to the classification of hyperspectral remote sensing data［D］.New York:State university of New York，College of Environmental Science and Forestry，2002.

［8］Antonio Plaza，Pablo Martínez，Rosa Pérez，et al.A quantitative and comparative analysis of endmember extraction algorithms from hyperspectral data［J］.IEEE Transactions on Geoscience and Remote Sensing，2004，42(3):650－663.

［9］Sun Li－xin，Zhang Ying，Bert Guindon.Improved iterative error analysis for endmember extraction from hyperspectral imagery［J］.Processing of SPIE，2008，7086: 11－18.

［10］李智勇，郁文贤，赵和鹏.迭代误差分析方法在高光谱异常检测中的应用［J］.系统工程与电子技术，2008，30(12):2340－2344.

Li Zhi－yong，Yu Wen－xian，Zhao He－peng.Application of iterative error analysis in hyperspectral anomaly detection［J］.Systems Engineering and Electronics，2008，30(12):2340－2344.

［11］谌德荣，孙波，陶鹏，等.基于核光谱角余弦的高光谱图像空间邻域聚类方法［J］.电子学报，2008，36 (10):1992－1995.

Chen De－rong，Sun Bo，Tao Peng，et al.Spatial neighboring clustering method for hyperspectral imagery based on kernel spectral angel cosine［J］.Acta Electronica Sinia，2008，36(10):1992－1995.