岩石三维图像重建算法分析

方莹莹，滕奇志，何小海，杨晓敏，李征骥

(1.四川大学电子信息学院，成都610064;2.四川大学图像信息研究所，成都610064)

研究储集层孔隙空间的几何形状和拓扑结构对石油地质实验工作有重要的意义。其中一项最重要的应用就是对储集层中的油气开采以及地质科学的研究分析。而真实岩石三维微观结构的直接测量方法，现在均是通过X射线同步断层显微成像技术(XCT)、核磁共振成像技术等得到，但XCT设备价格昂贵，核磁共振成像得到的图像分辨率不高，造成直接测量技术得不到广泛应用。故利用岩石样本的二维薄片图像进行三维微观结构重建是目前国内外研究的一个方向［1］。由于岩石的二维薄片图像反映了其三维结构固有的统计特性，利用薄片图像重建的三维结构，与真实三维结构在统计学上等价，能反映真实样本的特性，可用于储集层的特性研究，如微观孔隙结构、渗流特性等［2］。

目前国内外学者研究较多的三维图像重建方法主要有:模拟退火重建算法(SA)、基于傅里叶变换的高斯域截断算法(FFT)、基于多点地质统计重建算法(MPS)，以及基于这三种算法的一些改进算法。本文先对三类重建算法进行描述以及重建过程差别、重建时间进行对比分析，最后用三类算法对同一幅CT图进行重建，并对重建结果进行比较分析，得出综合性结论。

1 重建算法

1.1 基于快速傅里叶变换的截断高斯域方法

该算法基本思想是:利用Wiener－Khinchin定理，通过傅立叶变换生成具有与参考图像相同二阶统计分布的三维结构。由于傅立叶变换的结果需要利用孔隙度对其截取，因此这一方法又被称为基于快速傅里叶变换的截取高斯场重建方法。

基于FFT截断高斯域算法的重建过程为［3］: (1)首先计算二维参考图像的归一化两点自相关函数和孔隙度，其中，二维参考图像的归一化两点自相关函数是通过快速傅里叶变换得到;(2)将得到的归一化自相关函数转换为只与r相关的一维数组，并进行校正，经映射得到三维空间的自相关函数，此时三维空间自相关函数仍是与方向无关的一维数组;(3)根据对称性，获得三维空间三个方向的相关函数;(4)根据Wiener－Khinchin定理，对三维自相关函数做快速傅里叶变换，得到实数域的三维空间高斯场;(4)依据二维参考图像的孔隙度对该高斯场进行截断，得到由两相组成的(孔隙和颗粒)三维结构。

文献［2］提出了将粒子群优化算法(PSO)引入FFT算法中，目的是在不断的寻优过程中得到与二维参考图像最接近的三维空间的两点相关分布，使得重建过程最优。

1.2 基于模拟退火的重建算法

模拟退火算法的基本思想是［4］:通过不断变换两个不同相的点，寻找全局最优的重建结果。

重建过程为:(1)计算二维参考图像的归一化两点自相关函数(或者线性路径等统计特性参数)和孔隙度，并根据孔隙度随机生成具有相同孔隙度的三维结构;(2)随机寻找位于不同相位(孔隙相和岩石相)的两点进行交换，计算交换前后系统的能量;(3)根据Metropolis准则判断是否接受新生成的结构，如果接受，则用新结构代替原结构，否则保留原结构;(4)不断重复步骤(2)和步骤(3)，直至三维结构的能量低于设定值，或者交换次数大于设定的门限值。

1.3 基于多点地质统计的重建方法

MPS重建算法的基本思想是:使用参考图像把先验模型明确而定量地引入到建模当中，其最终模拟结果是由参考图像中的概率信息决定［5－6］。

MPS重建过程［7］是:(1)利用设定模板扫描二维参考图像，建立动态搜索树;(2)进行随机布点得到初始结构;(3)对每个待模拟点，在搜索树中搜取该待模拟点的条件数据概率，以此决定该待模拟点属于孔隙相或者岩石相;(4)遍历所有待模拟点，重复步骤(3)，直至所有待模拟点被准确布点［8］。

2 三种重建方法分析

重建时间方面:(1)FFT算法在计算二维参考图像两点相关函数以及获得三维空间高斯域时均采用了快速傅里叶变换，重建过程以秒为单位，重建时间最快;(2)PSO算法作为FFT算法优化算法，基本过程和FFT算法一致，但由于增加了多次找寻与参考图像最接近的自相关函数的步骤，所以其重建时间大幅增加，但重建时间仍少于SA和MPS算法;(3)MPS算法，重建过程中采用了搜索树的优化方法，将重建时间缩短，但重建过程中采用了三重模板进行重建，导致重建时间增加;(4)由于SA算法是个寻找全局最优的过程，在整个过程中，对每次交换前后的系统能量均需进行计算比较，为了重建结果达到最优，会在合适范围内选择尽可能更低的温度，以及更多的交换次数，故造成重建过程耗时较长。

重建的误差分析:(1)FFT重建过程中，为了加快重建速度，首先通过傅里叶变换得到二维图像的自相关函数，而其重建结果的三维自相关函数也是通过快速傅里叶变换得到的，但快速傅里叶变换对重建结构造成影响，引入一定误差;接着，由于重建得到的三维空间的函数是服从正太分布的连续实数，所以必须根据孔隙度对此连续实数进行截断，才能得到符合要求的两相三维结构，这使得重建结果的两相相对集中，导致结果出现误差。(2)PSO算法也会进行截断，故会出现结果偏差情况，但其三维结构的两点自相关函数是一个寻优过程的最优解，所以重建结果较FFT算法的形态以及连通性上更接近于真实结构。(3)理论上，SA算法是一种全局最优搜索算法，在约束函数的约束下，经过多次不同相位的两点交换、能量更新迭代后可以将初始的随机孔隙空间结构优化到与真实三维结构误差最小的最优状态。但由于SA算法中，选取的约束函数只是描述两点间关系的低阶函数，比如两点相关函数、线性路径函数等，虽然较FFT算法可以采用更多的结构信息，但并不能反映多孔介质中多个点之间的关系情况，所以使得采用SA算法重建得到的三维结构与原始多孔介质在连通性上有一定的偏差，不能很好地描述三维孔隙结构的长连通性。(4)MPS算法利用参考图像中的先验模型进行重建，将参考图像中多点间的相关性引入重建结构，避免了FFT和SA仅利用低阶统计信息而产生误差的情况，能很好地恢复孔隙相(或岩性)的几何形态(尤其是相边界)，因此其重建结果优于FFT和SA算法;但由于其重建结果需要参考图像的更多信息，故对参考图像的要求也更高。

3 重构实验结果分析

在本文中，使用三类重建算法，均是基于二维参考图片的统计特性，重建出与参考图像具有相同统计特性的三维图像。为了验证三类重建算法的正确性，我们选择CT扫描真实岩心获得的二维序列图像中的一幅，作为重建算法的参考图片，并以序列图构建真实岩心的三维结构作为标准，同时，为了定量分析重建效果，采用线性路径、局部孔隙度和局部渗透性三个分析函数，对三类算法重建结果进行分析比较。

图1是选取适合的参考图像(其中，白色部分表示孔隙)，图2(a)～图2(e)分别为CT序列图、FFT、PSO、SA以及MPS构建的1283像素大小的三维孔隙空间结构图(其中，图形中显示部分表示孔隙)。视觉形态上，发现SA和PSO算法重建结果相较于FFT和MPS更接近于真实三维结构，但是SA算法重建结果中存在许多孤立的颗粒(即孔隙)，造成连通性被破坏。同时，发现FFT算法重建三维结构尺寸明显大于真实结构，并且孔隙分布不均匀，较集中。而MPS算法出现很多模糊的边缘，需要进行多次平滑。该结果与理论分析相一致。

图1 砂岩二维参考图像Fig.1 Image of a thin section from sandstone

3.1 数字岩心线性路径分析

线性路径函数L(u，u+r)指长为r的线段［u，u+r］完全位于孔隙中的概率，是多孔介质结构的形态描述函数之一，其中包含一定的连通性信息。

图2 不同方法构建的1283像素大小的三维空隙空间结构图Fig.2 The pore space in a 1283 voxels subregion of samples CT，FFT，PSO，SA and MPS

图3为CT序列图和FFT+PSO、SA、和MPS三类算法重建结果线性路径函数的分布曲线。可以看出PSO和SA重建结果的曲线与CT序列图基本吻合，MPS和FFT重建结果与CT序列图差距较大，其中MPS曲线位于CT序列图曲线下方，而FFT位于其上方，再次说明MPS重建结果中孔隙的线性长度要小于CT序列图，而FFT则大于CT序列图。

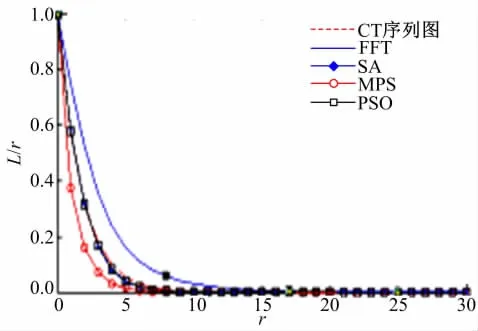
图3 原始CT序列，FFT，PSO，SA以及MPS线性路径曲线Fig.3 Linear path function for samples of CT，FFT，PSO，SA and MPS

3.2 数字岩心均质性分析

定义K(O，L)表示一个以O为多孔介质内部点为中心、L为边长的立方体的测量单元，在此测量单元中计算三维结构局部特征，如局部孔隙度、局部渗透性等。局部孔隙度分布函数:

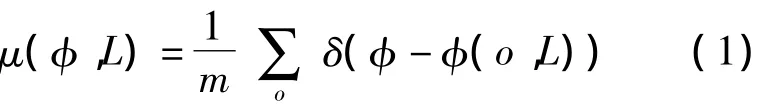
式中:m为测量单元的个数;δ(x)为狄拉克分布函数。当测量单元长度一定时，该函数曲线为孔隙度为φ的测量单元占所有测量单元的比例，它能反应三维结构中孔隙度的分布情况，分布越集中，曲线开口越小，三维结构均质性越好。

图4为CT序列图和FFT+PSO、SA、和MPS三类算法重建结果的局部孔隙度的分布曲线，取局部测量单元的边长L=450μm。从图4中可以看出MPS、SA、PSO曲线的峰值位置对应的孔隙度非常接近，是由于峰值位置对应的孔隙度为全局孔隙度，与理论一致。FFT曲线与其他四条曲线差异较大，因为L=450μm时，某些测量单完全位于FFT重建三维结构的岩石颗粒中，导致测量单元整体的孔隙度较小，再次说明FFT重建结果中岩石和孔隙尺寸均偏大。同样，SA曲线和MPS曲线的开口最小，其均质性优于PSO和FFT重建结果，而PSO均质性优于FFT。

图4 局部孔隙度分布曲线Fig.4 Lacal porosity distributions for sam ples CT，FFT，PSO，SA and M PS

3.3 局部渗透性结果分析

局部渗透性［9］是衡量某一孔隙度测量单元的连通性能函数，首先定义渗透特征函数为:

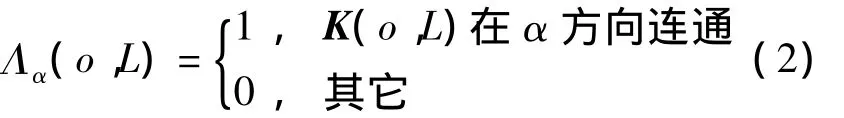
式中:α的取值为x、y、z、3、c，取3表示三个方向，c表示三个方向任意一个方向。当某个α方向上渗透特征函数为1时，表示该方向上，测量单元是连通的。

α方向上的局部渗流概率定义为［9］:

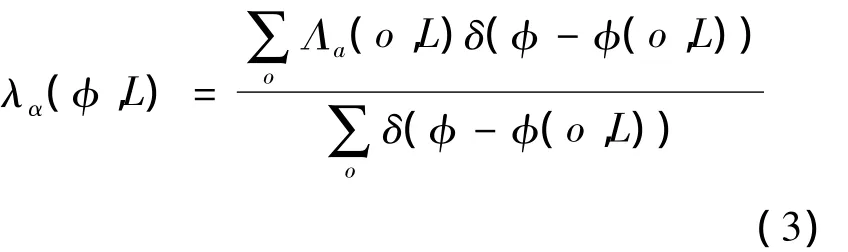
由式(3)可以看出，局部渗流概率表示孔隙度为φ的测量单元中，在α方向上连通的测量单元所占的比例。可以发现当特征长度L一定时，局部渗流概率曲线会随着局部孔隙度的增大而增大;渗流性越好的三维结构曲线，变化速度越快。

图5为CT序列图和三类算法重建结果的局部渗透性分布曲线，此时选取XYZ三个方向均连通的情况。对比曲线，可以发现当L=450μm时，MPS曲线最接近于真实三维结构，PSO次之，这两种重建结果均能较好的反映真实结构的连通特性;FFT三个方向的连通性最差。

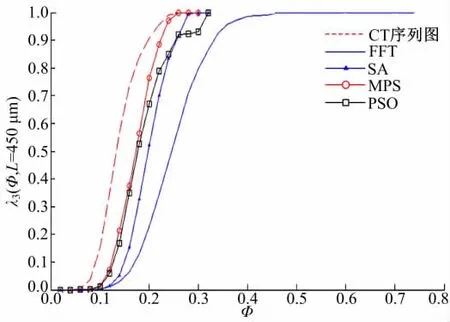
图5 原始CT序列，FFT，PSO，SA以及MPS局部渗透性曲线Fig.5 Fraction percolation cells versus L for samples of CT，FFT，PSO，SA and MPS

4 结束语

本文中，实现FFT(包含优化算法PSO)、SA、MPS三类重建算法对同一张真实的二维CT图片进行三维重建，通过分析比较三类重建结果与真实岩心的外观形态、低阶统计信息——线性路径、局部信息——局部孔隙度以及局部渗流概率，得出三类重建算法中MPS和PSO算法，较SA和FFT算法更加接近于真实岩心的孔隙岩石特征以及渗流特性，更能有效地描述岩石的微观特性。

［1］Kwiecien M J，Macdonald IF，Dullien F A L.Three－dimensional reconstruction of porous media from serial section data［J］.Journal of Microscopy，2011，159(3): 343－359.

［2］唐棠.基于二维图像的砂岩结构三.维重建及特性分析［M］.成都:四川大学，2009.

Tang Tang.Three－dimensional reconstruction and characterization of sandstonemicrostructure from two－dimensional images［M］.Chendu:Sichuan University，2009.

［3］Liang ZR，Fernandes C P，Magnani FS，et al.A reconstruction technique for three－dimensional porous media using image analysis and Fourier transforms［J］.Journal of Petroleum Science and Engineering，1998，21(3－4): 273－283.

［4］De Castro Martins.Image reconstruction using interval simulated annealing in electrical impedance tomography［J］.IEEE Engineering in Medicine and Biology Society， 2012，59(7):1861－1870.

［5］张挺.基于多点地质统计的多孔介质重构方法及实现［M］.合肥:中国科学技术大学，2009.

［6］BurcArpat G，Jef Caers.Conditional simulation with patterns［J］.Mathematical Geology，2007，39:2177－203.

［7］HiroshiOkabe，Martin JBlunt.Pore spac reconstruction usingmultiple point statistics［J］.Journal of Petroleum Sisticscience and Engineering，2005，46(1－2):121－137.

［8］黄丰.多孔介质模型的三维重构研究［M］.合肥:中国科学技术大学，2009.

［9］Jing Hu，Piet Stroeven.Local porosity analysis of pore structure in cement paste［J］.Cement and ConcreteResearch.2005，35(2):233－242.