共形阵低副瓣方向图综合性能分析

杨永建 樊晓光 王晟达 马 健

（空军工程大学航空航天工程学院，陕西 西安710038）

引 言

近年来，基本粒子群优化（Particle Swarm Optimization，PSO）算法［1-2］因其理论简单、易于编程实现且没有太多参数需要调整，取得了一系列研究成果，各种改进的PSO算法［3-5］可克服基本PSO算法早熟收敛、易陷入局部极值的问题.在阵列天线方向图综合中，PSO算法也取得了一系列研究成果［6-9］.尽管PSO算法及其改进算法在阵列综合中被证明是有效的，但PSO算法是一类不确定的算法，是一类概率型的全局优化算法，其收敛性因其随机因素的影响很难从数学上进行证明.根据文献［10］分析表明，PSO算法的收敛性与参数（如加速因子、迭代次数）的选取有关，但所选参数并不能保证PSO算法一定收敛.文献［11］从加速因子选取的角度对PSO算法的稳定性进行了分析，通过其所选的加速因子，可以保证PSO算法达到收敛，但其所需的迭代次数并不能精确计算，这表明即使PSO算法一定收敛，但其所需的迭代次数并不是固定的，每次试验所需的迭代次数不尽相同，这从侧面说明当迭代次数足够大时，一定能够保证PSO算法寻找到最优解.但在实际应用中，为了保证算法的有效性，迭代次数不可能设置的太大，因此，在迭代次数固定时，为了保证PSO算法的稳定性和有效性，对其性能分析应在统计意义下进行分析.目前，对于PSO算法有效性的分析大多是根据PSO算法是否能够达到要求进行分析的［6-8］.

本文通过定义有效性和稳定性两个性能指标，运用蒙特卡洛（Monte-Carlo）试验对PSO算法在阵列综合中的性能从统计角度进行了分析，并分析了不同阵列在运用二分粒子群优化（Dichotomy Particle Swarm Optimization，DPSO）算法进行综合时所能达到的最高性能及适应度函数对算法性能的影响.

1 PSO及DPSO算法

基本PSO算法的迭代公式如下：

式中：ω为惯性权重；c1和c2为学习因子，又称为加速因子；νki是第i个粒子当前运动速度向量；xki是第i个粒子的位置向量；pbest，i是第i个粒子自身历史的最优位置向量；gbest，i是群体的最优位置向量；rand1和rand2是（0，1）之间的随机数；上标k表示是第k次的迭代；下标d表示向量的第d维.

PSO算法在求解优化问题时，首先随机初始化一个种群，赋予其随机的位置和初速度.粒子在整个搜索空间飞行搜索，通过向自身最优和群体最优的不断学习，调整飞行速度，搜寻整个空间的最优解.每次飞行后都会更新个体最优值和群体最优值.当寻找到最优解或达到最大迭代次数，算法终止.这时的群体最优值即为求解得到的最优解.

文献［12］详细介绍了DPSO算法原理，验证了DPSO算法在阵列综合中的有效性.DPSO算法主要通过利用粒子本身的随机因素产生两个不同的分裂粒子，再通过对这两个分裂粒子的适应度值比较选优，选择具有较强寻优能力的粒子作为下一代粒子的本体参与下次的迭代.这符合“优胜劣汰”的生物进化规则，将大大提高粒子的寻优能力，减小算法所需的迭代次数.

2 低副瓣方向图性能分析

采用PSO算法或其改进算法进行低副瓣方向图综合时，主要从算法性能和所综合的方向图性能两个方面来考虑.主要影响因素有：

1）算法机制.不同的算法具有不同的收敛速度，且综合方向图性能也不尽相同.通常，一些改进算法会在原有算法的基础上提高算法的收敛速度或提高综合方向图的性能.

2）适应度函数构造.对同一问题构造不同的适应度函数会导致综合方向图结果的不同，不同的适应度函数可以从不同的角度对所综合的方向图性能进行改善.

3）阵列形式.不同的阵列形式有着不同的综合结果，分析不同阵列形式所综合的方向图性能有利于实际的决策.

2.1 适应度函数的选取

在综合低副瓣方向图时，适应度函数的选择应根据综合方向图的具体要求进行设计.文献［6-9］在综合低副瓣方向图时同时考虑了零陷的设置，文献［13］在综合低副瓣方向图时同时考虑了主瓣宽度的设置.

式中：α、β分别为权重系数；LMSL是最高旁瓣电平；LSLV是参考旁瓣电平；LNUL是最大零陷深度；LNLV是参考零陷深度.式（3）中第一项描述副瓣电平误差，第二项描述零陷误差.当综合低副瓣方图时，通常取α＝1，β＝0.

式中：LRSL为相对副瓣电平；AHP为主瓣半功率宽度角.在文献［13］中还给出了式（4）的其他改进表达式，这里不再讨论.

从低副瓣综合的要求来看，并不需要进行零陷的设置，并且如果进行多余的零陷设置可能造成收敛速度的下降.在综合低副瓣方向图时，考虑主瓣宽度是必要的，通常副瓣的降低必然会导致主瓣的展宽，但主瓣的展宽程度在一定范围内是可以修正的.为了直观地描述综合后方向图的性能，同时便于分析其有效性，这里直接取适应度函数为副瓣电平误差，有

2.2 基于统计的性能指标设计

为了分析PSO算法综合低副瓣方向图的性能，从统计的角度定义以下两个指标：

定义1：设Monte-Carlo试验次数为N，在N次试验结果中，有m次试验不满足设计要求，则算法的有效性值为

通常设计要求是有一个范围的，即在误差在一定范围内时，可以认为试验满足设计要求.这里定义当误差小于0.5dB时，认为试验满足设计要求.

定义2：将N次试验结果的误差值的方差定义为算法的稳定性值.

稳定性值越小，说明算法越稳定，粒子的活性较弱；反之，则算法稳定性较差，粒子的活性较强.粒子活性越强，粒子寻优能力越强，但并不能说稳定性值越大越有利于实际问题的解决，太大的稳定性值，会造成算法的稳定性较差，这在实际中是不允许的.

3 共形阵低副瓣方向图综合性能分析

均匀线阵、均匀圆环阵、圆柱共形阵和圆锥共形阵的阵列形式如图1所示，其中圆环上阵元均匀分布.

在阵元为全向阵元时，

1）均匀线阵的方向图函数为

式中：N为阵元数目；d为均匀线阵的间隔；an为第n个阵元的馈电电流幅值大小；βn为馈电相位，可由方向图指向唯一确定；k0＝2π/λ为自由空间的传播波数，λ为波长.

2）均匀圆环阵的方向图函数为

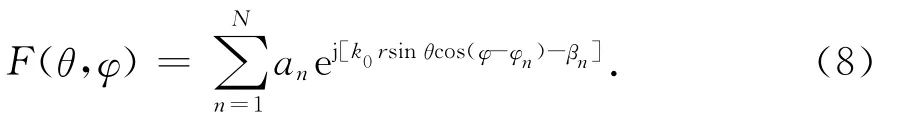
式中：r为圆环半径；φn＝2π（n-1）/N （n-1，2，…，N）表示阵元的方位角.

3）圆柱阵［12］的方向函数为

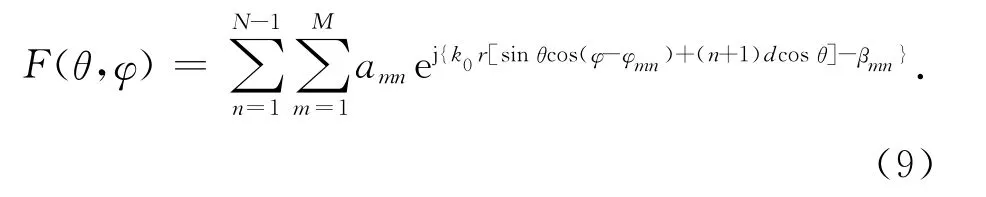
式中：amn表示第n层圆环上第m个阵元的馈电电流幅值；βmn为馈电相位；φmn表示该阵元的方位角；为相邻两层圆环间的间距.

4）圆锥阵的方向图函数为

式中：θn，φmn分别表示第n层阵元的俯仰角、第n层第m个阵元的方位角；rn为圆锥面上任意阵元到参考点的距离.

图1 阵列建模

仿真1 阵列综合中DPSO算法与PSO算法性能对比.仿真参数设置：Monte-Carlo试验次数N为50次，粒子规模为30，分别用DPSO算法和PSO算法对16元均匀线阵低副瓣方向图进行综合，参考副瓣电平为-30dB，最大迭代次数为50次.适应度函数如式（5）所示.

仿真结果：在50次 Monte-Carlo试验后，各次试验适应度函数的最小值所构成的曲线如图2所示.

仿真分析：从图2可以看出，DPSO算法的平均最小适应度值为-0.724dB，PSO 算法的为2.417 8dB.DPSO算法最小适应度值小于0.5dB的次数为47次，其有效性值为94%，PSO算法的为2次，其有效性值为4%.DPSO算法最小适应度值的方差为0.586 4，PSO算法的为3.011 3.可见DPSO算法其有效性和稳定性要大大优于PSO算法，是一种有效且稳定的算法.

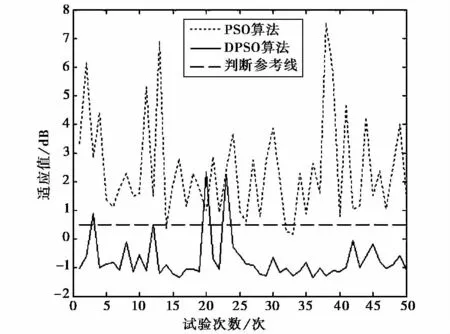
图2 线阵低副瓣综合时，适应度函数的最小值随实验次数的变化曲线

仿真2 DPSO算法在共形阵综合中的性能分析.

仿真参数设置：Monte-Carlo试验次数N为50次，粒子规模为30，参考副瓣电平为-30dB，最大迭代次数为50次.适应度函数如式（5）所示，主瓣宽度不要求.

仿真结果：在50次 Monte-Carlo试验后，各次试验适应度函数的最小值所构成的曲线如图3所示.

仿真分析：在采用式（5）的适应度函数时，由图3可以得出以下结论：

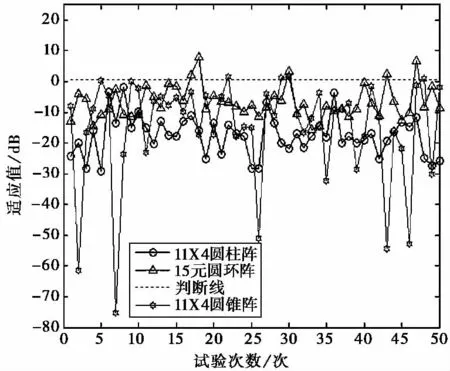
图3 三种阵列低副瓣综合时，适应度函数的最小值随实验次数的变化曲线

1）圆柱共形阵采用DPSO算法综合低于-30dB的方向图时，其有效性值为100%，可达到的最低副瓣电平约为-59dB，但此时有效性值仅为2%.副瓣电平的均值约为-37.6dB，若综合副瓣电平低于-37.6dB的方向图，其有效性值为58%.稳定性值约为41.2，其稳定性较差，粒子的活性较好.因此，如果对副瓣电平要求比较低，但最低不超过-59dB时，可以在增加迭代次数的条件下，使圆柱共形阵的副瓣电平达到期望值.

2）圆环阵采用DPSO算法综合低于-30dB的方向图时，其有效性值为92%，可达到的最低副瓣电平约为-45.6dB，但此时有效性值仅为2%.副瓣电平的均值约为-36.7dB，若综合副瓣电平低于-36.7dB的方向图，其有效性值为64%.稳定性值约为27.4.因此，如果对副瓣电平要求比较低，但不低于-45.6dB时，可以增加迭代次数，使副瓣电平达到期望值.

3）圆锥共形阵采用DPSO算法综合低于-30dB的方向图时，其有效性值为92%，可达到的最低副瓣电平约为-105dB，但此时有效性值仅为2%.副瓣电平的均值约为-45dB，若综合低于-45dB的方向图，其有效性值仅为10%.稳定性值约为296.3.因此，如果要求副瓣电平低于-105dB，其有效性值非常有可能为0，因为稳定性太差.

通过以上分析可以得出，在阵列方向图综合中，DPSO算法的综合性能不仅与最大迭代次数有关，而且与阵列形式有着密切的关系.其中圆锥共形阵运用DPSO算法时所能达到的副瓣电平很低，但其主瓣宽度展宽非常严重，需要对其主瓣宽度进行控制.

仿真3 适应度函数对DPSO算法性能影响分析.

仿真参数设置：Monte-Carlo试验次数N为50次，粒子规模为30，参考副瓣电平为-30dB，最大迭代次数为50次，圆柱、圆锥共形阵阵列形式与仿真2相同.适应度函数为式（5）取绝对值.

仿真结果：在50次 Monte-Carlo试验后，各次试验适应度函数的最小值所构成的曲线如图4所示.

图4 共形阵低副瓣方向图综合时，适应度函数的最小值随实验次数的变化曲线

仿真分析：在对适应度函数取绝对值后，由图4可以得出以下结论：

1）圆柱共形阵的平均最小适应度值约为0.002 6dB，其 稳 定 性 值 为 0.000 4，有 效 性 为100%.

2）圆锥共形阵的平均最小适应度值约为0.053 7dB，其稳定性值为0.079 0，有效性为98%.

对比仿真2中DPSO算法在圆柱、圆锥共形阵的性能，可以看出DPSO算法的性能与适应度函数的构造有密切的关系.所采用的两种适应度函数从不同方面对算法的性能进行了说明：若对适应度函数不取绝对值，则有利于分析DPSO算法在不同副瓣电平要求下所能达到的性能；若对适应度函数取绝对值，则有利于从实际要求的角度分析DPSO算法的性能.

从以上三个仿真可以看出，运用DPSO算法进行阵列方向图综合时，DPSO算法的性能可从有效性、稳定性两个方面进行说明.DPSO算法的性能与迭代次数、阵列形式和适应度函数的构造有着密切的关系.

4 结 论

文章通过定义有效性值和稳定性值两个参数对PSO算法在阵列综合中的性能从统计的角度进行了分析.通过分析PSO算法与DPSO算法在线阵低副瓣综合中的性能，说明了DPSO算法的高效性、有效性和稳定性.通过分析圆环阵、圆锥阵和圆柱阵低副瓣综合中的性能，说明了DPSO算法与阵列形式密切相关，有利于阵列形式的选择.通过对适应度函数取绝对值，分析了DPSO算法在圆柱阵和圆锥阵低副瓣综合中的性能，说明了适应度函数对DPSO算法性能的影响.仿真分析表明所定义的两个性能指标完全可以从实际应用角度分析算法性能及阵列形式的选择，具有较强的实际应用指导意义.

［1］SHI Yuhui，EBERHART R C.Emprical study of particle swarm optimization［C］∥Proc of the Congress on Evolutionary Computation.Washington D C，1999：1945-1950..

［2］BOERINGER D W，WERNER D H.Particle swarm optimization versus genetic algorithms for phased array synthesis［J］.IEEE Trans on Antennas and Propagation，2004，52（3）：771-779.

［3］SHI Y，EBERHART R C.A modified particle swarm optimizer［C］∥Proceeding of the IEEE Congress on Evolutionary Computation（CEC 1998）.Piscataway，1998：69-73.

［4］EBERHART R C，SHI Y.Comparing inertia weights and constriction factors in particle swarm optimization［C］∥ Proceedings of the 2000Congress on Evolutionary Computation.La Jolla，2000，1：84-88.

［5］EBERHART R C，SHI Y.Fuzzy adaptive particle swarm optimization［C］∥ Proceedings of the Congress on Evolutionary Computation.Seoul，2001，1：101-106.

［6］焦永昌，杨 科，陈胜兵，等.粒子群优化算法用于阵列天线方向图综合设计［J］.电波科学学报，2006，21（1）：16-20.JIAO Yongchang，YANG Ke，CHEN Shengbing.Application of particle swarm optimization in antenna array pattern synthesis［J］.Chinese Journal of Radio Science，2006，21（1）：16-20.（in Chinese）

［7］金荣洪，袁智皓，耿军平.基于改进粒子群算法的天线方向图综合技术［J］.电波科学学报，2006，21（6）：873-877.JIN Ronghong，YUAN Zhihao，GENG Junping，et al.The pattern synthesis of antennas based on a modified particle swarm optimization algorithm［J］.Chinese Journal of Radio Science，2006，21（6）：873-877.（in Chinese）

［8］刘 东，冯全源.基于停滞检测粒子群算法的阵列天线方向图综合［J］.电波科学学报，2009，24（4）：697-700.LIU Dong，FENG Quanyuan.Pattern synthesis of antennas based on modified PSO algorithm with stagnation dection［J］.Chinese Journal of Radio Science，2009，24（4）：697-700.（in Chinese）

［9］肖龙帅，黄 华，夏建刚，等.基于近邻粒子群优化的阵列天线方向图综合［J］.通信技术，2009，42（9）：52-53.XIAO Longshuai，HUANG Hua，XIA Jiangang，et al.Array antennas beam pattern synthesis based on neighborhood particle swarm optimization ［J］.Communications Technology，2009，42（09）：52-53.（in Chinese）

［10］高 尚，杨静宇.群智能算法及其应用［M］.中国水利水电出版社，2006：112-117.

［11］张 玮，王华奎.粒子群算法稳定性的参数选择策略分析［J］.系纺仿真学报，2009，21（14）：4339-4334.ZHANG Wei，WANG Huakuai.Analysis on parameter selection for stability of particle swarm optimization algorithm［J］.Journal of System Simulation，2009，24（4）：697-700.（in Chinese）

［12］杨永建，王晟达，马 健，等.基于改进粒子群算法的共形阵列天线综合［J］.现代雷达，2012，34（12）：64-67.YANG Yongjian，WANG Shengda，MA Jian，et al.Conformal antenna array beam pattern synthesis based on improved particle swarm optimization ［J］.Modern Radar，2012，34（12）：64-67.（in Chinese）

［13］TIAN Yubo，QIAN Jian.Improve the performance of a linear array by changing the spaces among array elements in terms of genetic algorithm［J］.IEEE Transactions on Antennas and Propagation，2005，53：2226-2230.