宽带高斯型功率谱噪声信号相关特性分析

王 钊 顾 红 苏卫民 樊劲宇

（南京理工大学电子工程与光电技术学院，江苏 南京210094）

引 言

宽带随机信号具有测距精度高、距离速度无模糊、截获概率低、抗干扰能力强等优点，被广泛应用于雷达系统［1-4］.在宽带雷达中，高速运动目标的回波不仅表现为多普勒频移，也表现为回波包络（或带宽）的压缩或展宽，这种现象称为多普勒色散现象［5-6］.相关函数是雷达匹配滤波器输出的结果，它是雷达的分辨力及检测性能分析的基础，多普勒色散现象的存在使得窄带相关函数不再适用，很多学者对随机信号的宽带相关函数进行了研究，但是研究都局限在多普勒色散积较小的情况，讨论也并不完整［7-8］.

Remley，W.R.通过理论推导，分析了多普勒色散效应对矩形谱宽带随机信号相关输出的影响，但是由于矩形谱宽带随机信号的限制，使得分析过程中忽略了载波的多普勒频率对相关输出的影响［9］.Sune R.J.Axelsson针对矩形谱随机信号旁瓣较高的缺点，提出了无旁瓣的高斯谱随机信号，并分析了其抗干扰性能，同时分析了其宽带平均相关函数，但是并没有给出闭合的表达式，也没有分析多普勒色散积较大的情况［8，10-11］.

利用高斯谱噪声调频信号来产生高斯谱的噪声信号，推导了高斯谱随机信号宽带相关函数均值的解析表达式，通过计算机仿真验证了表达式的正确性.在此基础上分析了高斯谱随机信号的宽带相关函数在多普勒色散积较大的情况下出现双峰的特点并解释了其原因，讨论了宽带相关函数的双峰宽度与多普勒色散积的关系，以及双峰位置与相对带宽的关系.上述分析为宽带高斯谱噪声雷达的分辨力和检测性能分析以及系统的参数设计提供了理论基础.

1 信号模型

雷达发射噪声调频信号的表达式为

式中：Aσ表示目标的幅度衰减因子；Ar＝AσA表示回波幅度；α＝（c-v）/（c＋v）为时间尺度因子；τ0＝2R0/（c-v）为初始距离的延时；c为光速.当多普勒色散积γ远小于1时，回波模型退化为窄带模型［12］，其中多普勒色散积定义为

式中：B表示信号带宽；T表示信号时宽.

当e（t′）为均值为0，方差为σ2n的带限高斯白噪声时，其概率密度函数为

式中ΔFn表示高斯白噪声的带宽，其功率谱密度为

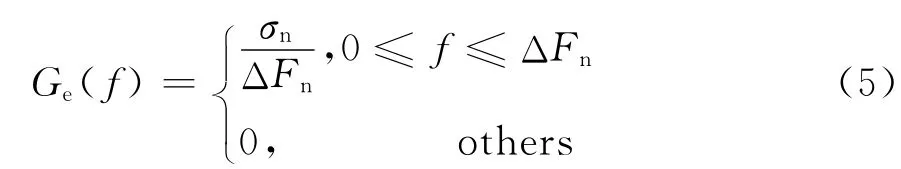
令mfe＝KFMσn/ΔFn.当mfe＞＞1时，噪声调频信号的功率谱密度Gs（f）与调制噪声的概率密度函数f（e（t′））呈线性关系，于是噪声调频信号的功率谱密度亦为高斯型

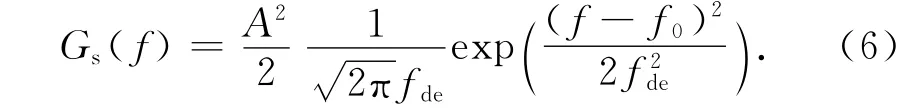
式中fde＝KFMσn.当mfe＞＞1时，噪声调频信号的带宽为可见噪声调频信号的带宽与调制噪声的带宽没有关系，而与其方差和调制指数成线性关系［13］.由式（6），根据维纳-辛钦定理可得噪声调频信号归一化自相关函数为［14］

本文讨论的宽带高斯谱噪声信号以宽带高斯谱噪声调频信号为例展开，所得到的结论适用于其他宽带高斯谱噪声信号.涉及的高斯谱噪声信号都是由高斯谱噪声调频信号所代替.

2 高斯谱噪声信号的宽带相关函数

根据式（2）给出的噪声调频信号的宽带回波模型，宽带信号的相关函数定义为［10］

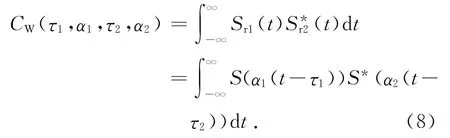
式中，α1，τ1与α2，τ2分别表示参考信号与回波信号的尺度因子及延迟时间，令α＝α1/α2，τ＝α2（τ1-τ2），则式（8）可写为

且当α＝1，τ＝0时，参考信号与回波信号完全相关，宽带相关函数的相关峰最高.将式（2）带入式（9），可得

式中Aχ＝Arexp（j2πf0ατ）为常数项.

时宽带宽积大的噪声信号的相关函数特性接近于它的均值，于是对式（10）取均值运算，可以得到

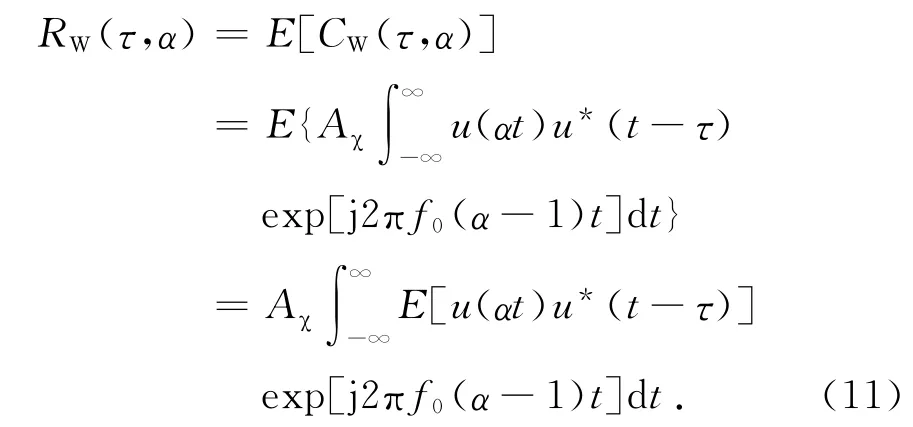
式中E［u（αt）u＊（t-τ）］为平稳随机过程u（t）的自相关函数，且只与时间差有关，可以写为

式中：U表示信号能量；T为信号持续时间；ε＝1-α.因此，式（12）可写为

当v＜＜c时，式（13）可以写为

式中：fd＝2vf0/c为多普勒频率；τ＝2R/c为延时.将式（7）代入式（14）得到高斯谱随机信号的宽带相关函数的均值表达式

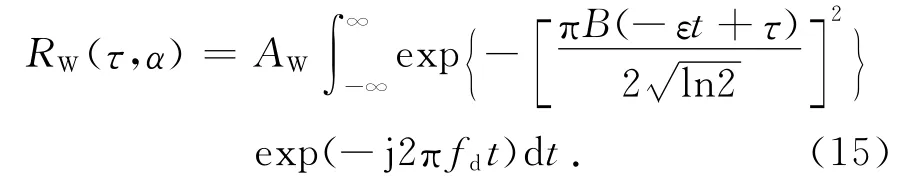
式中AW＝AχU/T.由于此时回波信号时宽为T/α时，积分限取 ［-T/（2α），T/（2α）］，可得

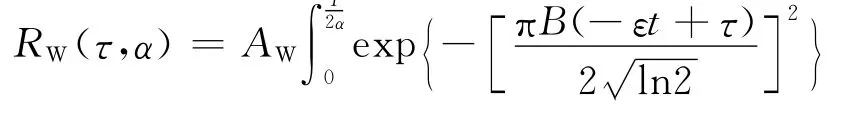
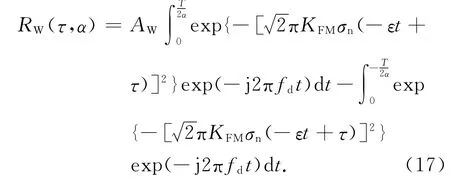
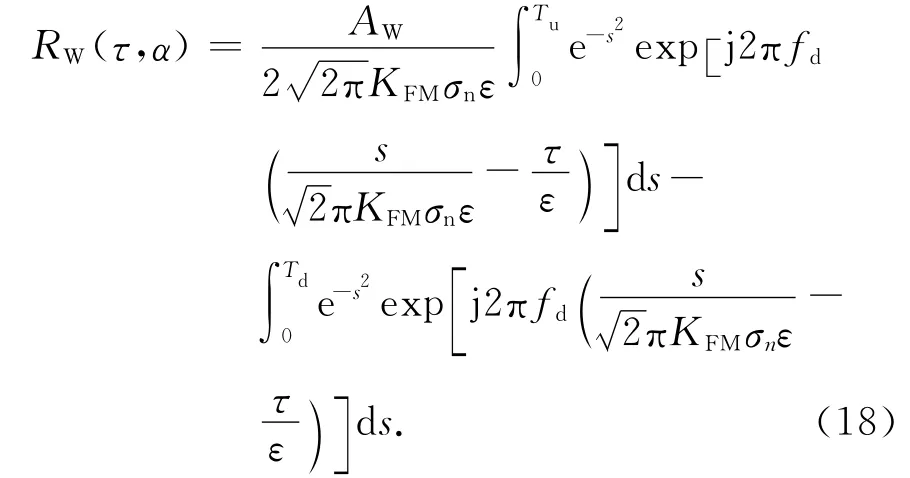
3 仿真验证

本节通过计算机仿真验证上述相关函数的正确性.噪声调频信号载频f0＝1GHz，处理时宽T＝30μs，采样频率fs＝2.5GHz，调制基带噪声为标准正态分布，带宽为Bb＝100MHz，调制指数为KFM＝212.33MHz，mfe＝KFMσn/ΔFn＝2.12，满足条件mfe＞＞1，经计算得噪声调频信号带宽B＝500MHz.此时信号带宽为500MHz，相对带宽为50%，满足宽带信号要求.

图1对比了仿真数据与理论数据的结果.图1（a）和（b）分别给出了多普勒色散积γ为0和2时的宽带相关函数输出以及主峰放大以后的仿真结果及理论结果，其中求取仿真结果样本均值时的Monte Carlo实验次数为50.从图1可以看出，在γ＝0时，理论结果与仿真结果绘制所得的两条曲线几乎重合，在γ＝2时，两条曲线存在微小的偏差，这主要由于噪声调频信号的随机性，当信号处理的时长有限时，其匹配滤波器的输出存在一个噪声基底［11］.同时，从图1（b）可以看出宽带相关输出在γ＝2时会出现双峰，且双峰的位置分别位于0和2距离门处.仿真实验验证了本文推导的宽带高斯谱噪声相关函数的正确性.

图1 理论准确性分析

根据宽带相关函数，可以得到其宽带平均模糊函数的表达式［11］

图2给出了高斯谱随机信号宽带平均模糊函数与窄带平均模糊函数.图2（a）给出了f0＝2B时，根据式（20）绘制的高斯谱随机信号宽带平均模糊函数的理论结果，其中多普勒色散积在-5～5之间搜索，搜索步长为0.01，对应的目标速度范围为［-50km/s，50km/s］，以同样的目标速度绘制窄带平均模糊函数，如图2（b）所示.从图2可以看出宽带平均与窄带平均模糊函数虽然同为图钉型模糊函数.但是窄带平均模糊函数仅存在一条穿越0距离门的主脊，而宽带平均模糊函数不仅存在一条穿越0距离门的主脊，同时存在一条斜跨0距离门的主脊背，这主要是由于宽带平均模糊函数在多普勒色散积较大时出现双峰现象导致.

图2 高斯谱噪声信号平均模糊函数

图3给出了多普勒色散积不同时的宽带相关函数.图3（a）为f0＝B/2时，多普勒色散积γ＝-5，-3，-1，1，3，5时宽带相关函数结果.可以看到，随着多普勒色散积的增加，宽带相关函数的峰值下降并展宽，当多普勒色散积大于3时，主峰的两端出现突起，类似双峰.图3（b）为f0＝2B时，多普勒色散积γ＝-5，-3，-1，1，3，5时宽带相关函数结果.可以看到，随着多普勒色散积的增大，宽带相关函数出现明显的双峰现象，双峰之间的距离伴随多普勒色散积的增大而渐远且幅值降低，其中一个峰始终保持在0距离门，而另一个峰所处的距离门与多普勒色散积相同.由此可见，双峰的特性不但与多普勒色散积有关，也和载频相关.下面将对这类双峰现象展开研究.

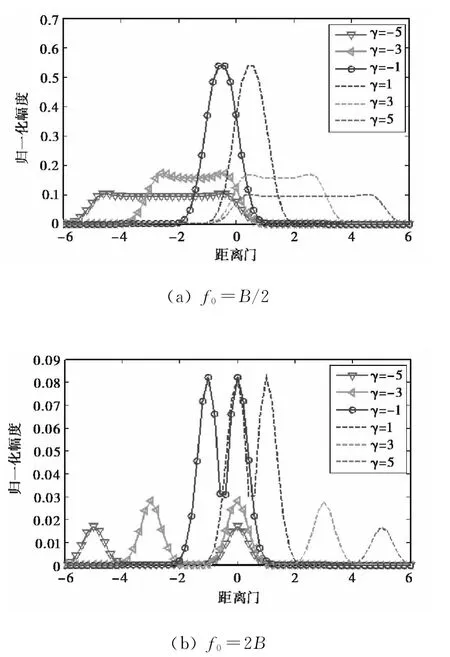
图3 多普勒色散积对宽带相关输出的影响

4 宽带相关函数特性分析

当v＜＜c时，宽带相关函数的表达式可以写为

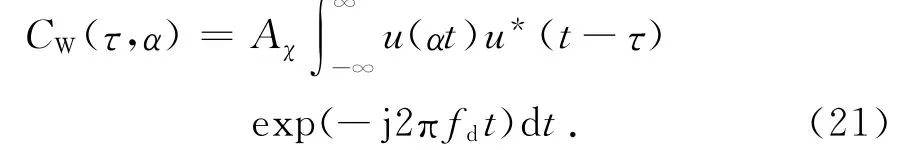
将宽带相关函数分为两个部分，一部分是m（t，τ）＝u（αt）u＊（t-τ），表示了回波信号与参考信号的滑动共轭相乘的过程，另一部分是j2πfdt）dt，表示了m（t，τ）在载波多普勒频率fd频点的能量.也就是说宽带相关函数便是回波信号与参考信号滑动共轭相乘的结果在载波多普勒频率fd频点的能量.

在窄带噪声信号滑动共轭相乘的过程中，当回波信号与参考信号之间的时延为零时，定义为0距离门，此时的参考信号与回波信号完全相关，完全相关的地方共轭相乘以后为直流.由于噪声信号的随机性，在非0距离门处，回波信号与参考信号之间是完全不相关的，完全不相关的地方共轭相乘以后仍为随机信号.

对于宽带信号来说，当多普勒色散积较大时，回波信号相对于参考信号会发生时间上的压缩或展宽，使得其滑动共轭相乘的过程与窄带信号有所不同.假设v≪c，其信号的采样间隔为ts，将m（t，τ）＝u（αt）u＊（t-τ）展开，并表示为离散形式，可以得到

式中：2vnts/c表示回波信号的时延；τ表示参考信号的时延.可以看出对于回波信号的不同样点，其时延是时变的，且样点之间时延的变化量固定为2vts/c.距离门为零时，τ＝0，假设回波信号样点n1的时延2vn1ts/c＝1/B，当时延大于一个距离门时信号完全不相关，则只有在n＜n1＝c/（2vBts）时的回波信号与参考信号是相关的，这里认为距离门为0时的参考信号与回波信号为部分相关.距离门为1时，τ＝1/B，假设样点n2的时延2vn2ts/c-τ＝0，样点n3的时延2vn3ts/c-τ＝1/B时，则只有在0＜n＜n3＝c/（vBts）之间的回波信号与参考信号都是相关的，这里同样可以定义为部分相关.同理，距离门为ρ时，τ＝ρ/B，则（ρ-1）c/（2vBts）＜n＜ （ρ＋1）c/（2vBts）之间的回波信号与参考信号是相关的.为了保证样点的取值在信号时宽内，需要满足0＜n＜T/ts，而时宽T与多普勒色散积γ的关系为T＝γc/（2vB），于是可得0＜n＜γc/（2vBts）.结合上面的表达式，可以得出宽带噪声信号在滑动的过程中是一个部分相关的过程，且在距离门为ρ时，回波信号与参考信号的相关部分出现的样点为

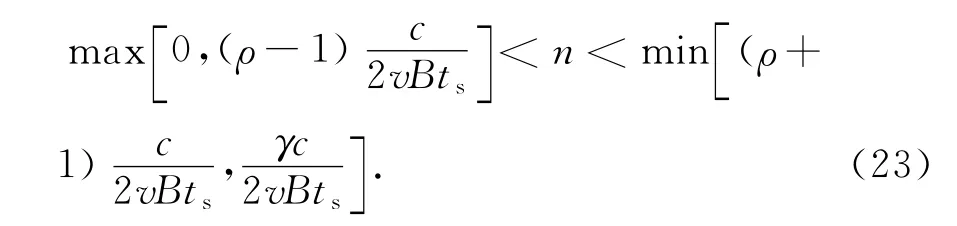
为了能具体说明问题，进行如下仿真.噪声调频信号载频f0＝400Hz，处理时宽T＝1s，采样频率fs＝1 000Hz，调制基带噪声为标准正态分布，带宽为Bb＝40Hz，调制指数为KFM＝84.93Hz，mfe＝KFMσn/ΔFn＝84.93Hz/40Hz＝2.12，满足条件mfe＞＞1，计算得噪声调频信号带宽为B＝200 Hz.此时信号的相对带宽为50%，仍然满足宽带信号要求.假设此时的多普勒色散积为2.那么根据上面的推导，可知0～2距离门处会有部分信号相关的情况出现，根据式（23）可知，当距离门为0，1和2时，信 号 相 关 的 部 分 分 别 为 ［0，c/（2vBts）］，［0，c/（vBts）］，［c/（2vBts），c/（vBts）］.很明显，当距离门为0和2时，信号相关的部分较少，而距离门为1时，信号相关的部分较多.从而可以推断出共轭相乘以后的结果，0和2距离门处直流分量较低，1距离门处直流分量较高.图4为m（t，τ）在0，1和2距离门处的波形，其中实线为单次样本的仿真结果，虚线为多次样本的统计结果.图4（a）为m（t，τ）在第0距离门的实部与虚部波形，此时信号的左端存在直流分量，直流分量的能量为图4（a）中虚线所包围的区域.图4（b）为m（t，τ）在第1距离门的实部与虚部波形，此时信号的中间部分出现直流分量，直流分量的能量为图4（b）中虚线所包围的区域，可以看出此时包围的区域近似为为图4（a）的二倍.图4（c）为m（t，τ）在第2距离门的实部与虚部波形，此时信号的右端出现直流分量，直流分量的能量为图4（c）中虚线所包围的区域，与图4（a）相同.

图4 参考信号与回波信号共轭移位相乘的结果

由于信号的总能量是固定的，当直流分量能量较高时，非直流分量的能量便会降低，并且随着频率的增大，能量降低越明显.由于宽带信号的相关结果可以表示为m（t，τ）在多普勒频率点fd处的能量，通过分析的m（t，τ）的能量分布，便可以得出宽带信号的相关特性.载波多普勒频率接近零时，宽带相关函数表示了直流分量的能量，因此相关函数在距离门为1处的幅值将大于距离门为0和2处的幅值，相关函数呈单峰形式.当载波多普勒频率增加时，宽带相关函数表示了非直流分量的能量，因此相关函数在距离门为1处的幅值将小于距离门为0和2处的幅值，相关函数在距离门0以及距离门2处出现双峰.图5给出了多普勒为0和4/T时的相关结果的统计值，可以看出，当多普勒为0时，相关峰呈现单峰形式，但是单峰跨越多个距离门，当多普勒为4/T时，相关峰呈现双峰形式，分别位于0和2距离门.由于信号的载波多普勒频率为fd＝f0（α-1），那么在尺度因子α固定时，载波多普勒频率的大小由信号的载波决定，从而信号载波的取值也决定了相关峰的形状.

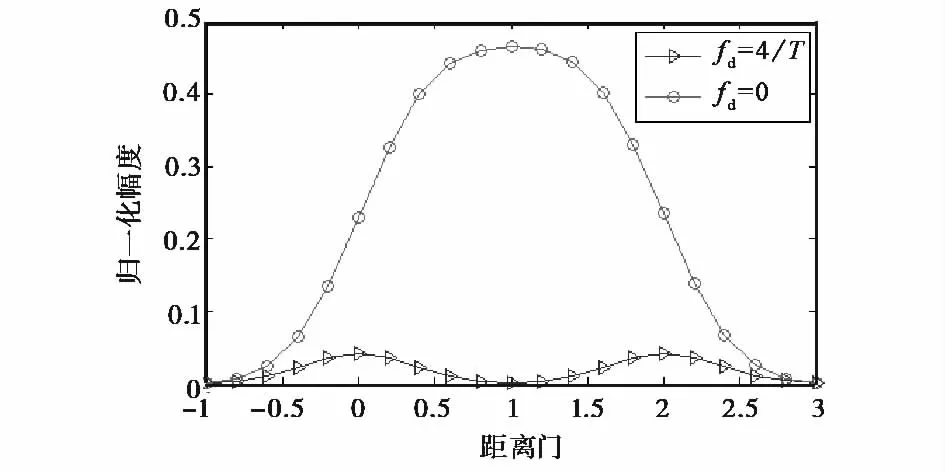
图5 载波多普勒不同时相关结果比较（统计值）

上面分析了多普勒色散积为2时的情况，m（t，τ）部分相关时的距离门为0，1和2，而双峰出现在0和2距离门处.这个结论可以很容易地扩展到多普勒色散积大于2时的情况，当多普勒色散积为γ时，出现部分相关的距离门将为0，1，2，…，γ，在距离门0和γ处将出现双峰.然而实际上，双峰的位置只有在载波多普勒频率较大时才会出现在距离门0和γ处，下面的仿真将说明这一问题.

图6给出了多普勒色散积γ＝2，3，4，信号相对带宽在0.2到2之间变化时，宽带相关函数双峰位置的变化曲线.可以看出，当信号相对带宽较高时，双峰的位置会随着相对带宽的减小而逐渐远离，当相对带宽等于1时，双峰的偏移量达到最大，分别在0和γ处出现双峰，而后相对带宽的减小将不影响双峰的位置.由此可得，多普勒色散积决定了双峰的最大距离，而相对带宽则决定了双峰的分离程度.

图6 多普勒色散积与双峰位置的关系

5 结 论

本文利用高斯谱噪声调频信号进行宽带回波信号的分析，推导了高斯谱噪声调频信号的宽带相关函数均值解析表达式，并通过仿真验证了表达式的正确性，为进一步定量分析高斯谱宽带噪声信号的分辨力及检测性能提供了理论基础.基于所得表达式分析了宽带相关函数的特性，得出在多普勒色散积较大时宽带相关函数产生双峰的结论，并证明了其双峰是由于回波的尺度变换，从而在多个距离门内出现部分相关的情况所导致.而后讨论了双峰位置与多普勒色散积及相对带宽之间的关系，得出多普勒色散积决定了双峰的最大距离，而相对带宽决定了双峰的分离程度的结论，为宽带噪声雷达系统的参数设计提供了依据.下一步工作将主要为宽带噪声信号的分辨力及检测性能的研究，以及如何在双峰存在的情况下有效地检测目标.

［1］CHEN W J，NARAYANAN R M.Comparison of the estimation performance of coherent and non-coherent ambiguity functions for an ultrawideband multi-inputmulti-output noise radar［J］.IET Radar，Sonar ＆ Navigation，2012，6（1）：49-59.

［2］SUN H，LU Y，LIU G.Ultra-wideband technology and random signal radar：an ideal combination［J］.IEEE Aerospace and Electronic Systems Magazine，2003，18（11）：3-7.

［3］LIU G，GU H，SU W.Development of random signal radars［J］.IEEE Transactions on Aerospace and Electronic Systems，1999，35（3）：770-777.

［4］张新相，吴铁平，陈天麒.随机信号雷达抗干扰性能分析［J］.电波科学学报，2008（1）：189-194.ZHANG Xinxiang，WU Tieping，CHEN Tianqi.ECCM capabilities of random signal radar［J］.Chinese Journal of Radio Science，2008（1）：189-194.（in Chinese）

［5］WEISS L G.Wavelets and wideband correlation processing［J］.IEEE Signal Processing Magazine，1994，11（1）：13-32.

［6］陈隽永，徐继麟.宽带信号模型及分辨力性能研究［J］.电波科学学报，2001（1）：128-130.CHEN Juanyong，Xu Jilin.Reaserch on the model and resolution of wideband signal［J］.Chinese Journal of Radio Science，2001（1）：128-130.（in Chinese）

［7］DAWOOD M，NARAYANAN R M.Generalised wideband ambiguity function of a coherent ultrawideband random noise radar［C］∥Radar，Sonar and Navigation，IEE Proceedings，2003，150（5）：379-386.

［8］AXELSSON S R J.Random noise radar/sodar with ultrawideband waveforms［J］.IEEE Transactions on Geoscience and Remote Sensing，2007，45（5）：1099-1114.

［9］REMLEY W R.Doppler dispersion effects in matched filter detection and resolution［J］.Proceedings of the IEEE，1966，54（1）：33-39.

［10］AXELSSON S R J.Generalized ambiguity functions for ultra wide band random waveforms［C］∥International Radar Symposium，2006.

［11］AXELSSON S R J.Noise radar using random phase and frequency modulation［J］.IEEE Transactions on Geoscience and Remote Sensing，2004，42（11）：2370-2384.

［12］KELLY E J，WISHNER R P.Matched-filter theory for high-velocity，accelerating targets［J］.IEEE Transactions on Military Electronics，1965，9（1）：56-69.

［13］LÜJ，GU H，SU W.High speed target echo modeling of noise frequency modulated signal radar［C］∥IET Radar Conference，Guilin，2009.

［14］武 昕，李 澍，刘 畅，等.基于特征参数的随机噪声雷达相关输出研究［J］.电波科学学报，2012（3）：543-550.WU Xin，LI Shu，LIU Chang，et al.Correlation output of random noise radar based on characteristic parameters［J］.Chinese Journal of Radio Science，2012（3）：543-550.（in Chinese）