认知频谱切换延时及用户容量的排队论分析

王 玲 彭启琮 彭启航

（上海电力学院电子与信息工程学院，上海200090）

引 言

随着无线多媒体应用的发展，频谱资源日益紧张，而且但大量研究表明传统的固定频谱分配方式导致频段在某些时间和空间上未被充分利用.认知无线电［1］是能够伺机利用授权用户没有使用的频谱空洞进行通信的技术，它的出现为减轻频谱资源的巨大压力提供了理论支持.

过去十年针对认知无线电的研究主要集中于物理层的频谱检测和频谱共享；而保障认知用户服务质量的多媒体接入控制（Media Access Control，MAC）子层控制机制也在近年得到越来越多的关注.由于授权用户有优先使用频谱的权限，在授权用户开始通信时认知用户必须立即空出占用的信道.因此，频谱切换在认知用户保持链接及重返未完成传输的过程中扮演着重要的角色.在传统无线通信系统中，频谱切换仅出现于用户移动至蜂窝小区之外或者信号衰落时［2］.与此相比，认知无线电网络中，当授权用户出现在共享的频段内，认知用户则可能需要进行频谱切换以保持通信.这导致认知频谱切换将更加频繁并且与授权用户的行为紧密相关.

可用频谱资源的不固定为设计频谱切换机制引入了新的挑战.实际上，认知用户要在时变的可用频段中选取切换目标信道，以及确保尽可能小的性能衰减是非常困难的.文献［3］提出了一种单用户最优的MAC层短视检测接入算法，采用轮循机制在每个时隙选择合适的信道进行接入和传输.文献［4］则通过预测主用户行为，对待检测的信道排序，将搜索频谱机会的延时尽可能缩短.而文献［5］在数据传输的同时进行空闲信道搜索，也为了达到缩短切换延时的目的.上述文献虽然考虑了频谱切换延时，但侧重于分析不同检测机制与搜索频谱机会延时之间的关系.我们注意到频谱切换延时不仅取决于搜寻可用信道的时长，还与授权用户以及认知用户对目标信道的占用方式有关系.文献［6-8］提出了一种占先重返（Preemptive Resume，PR）模型，在没有其他空闲信道的情况下，认知用户的频谱切换是在原信道上完成的；而文献［9］则对这种不转移信道的认知服务时长做了排队论分析.这类机制有效地保持了认知数据链接，但重新获得数据传输的延时可能过长，这对延时敏感的服务是不能被接受的.［10-11］均针对认知无线电IP电话（Voice over IP，VoIP）服务中由于授权用户介入导致的丢包率，以及服务质量（Quality of Service，QoS）限制下的系统容量做出了分析.其中文献［11］还利用大偏差理论得到了VoIP系统中有效带宽和有效容量的数学表达.但上述文献仅给出了到达速率为常数的数据包级别的延时分析，并没有涉及用户级别的频谱切换延时以及切换超时所导致的强制中断率这一QoS标准.

本文将从授权用户行为入手，着重分析由授权和认知用户交通信息影响的频谱切换延时.提出一种虚拟排队切换模型用于推导出切换延时的解析表达式，进而引出强制中断率限制条件下的用户容量的定义.给出仿真结果和数值分析证明本文算法的有效性.

1 系统模型

本文中的认知无线电系统包含C个信道，用户传输数据以时隙为时间单位，并且一个用户（授权用户或认知用户）同时最多只占用一个信道.授权用户享有最高的优先级，在其开始传输数据时，认知用户需要频谱切换以避免对授权用户的干扰.

1.1 频谱切换延时

首先定义频谱切换延时为认知用户传输被授权用户打断时刻至寻找到新的空闲信道恢复传输时刻的区间［8］.如图1所示，认知用户SU1被打断后系统中所有信道都为授权用户或其他认知用户占用；W 时隙后出现了新的频谱机会，SU1经历时长Ts搜索到空闲信道，将工作信道更新为信道2，从而完成了一次频谱切换.需要注意的是如果新的频谱机会先出现在认知用户原工作信道上，这样的重返传输本文也认定为频谱切换，这与传统通信系统中的频谱切换的定义是有区别的.将频谱切换延时表示为

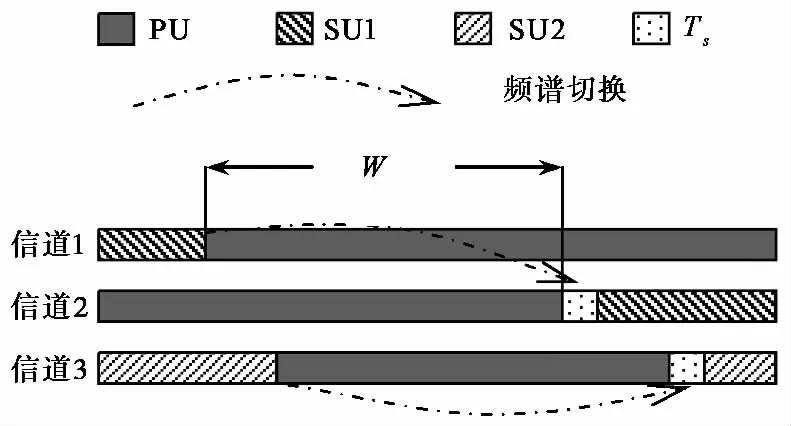
图1 认知无线电频谱切换及延时

式中，Ts是检测和搜索空闲信道的时间，由 MAC层检测机制决定，但这不是本文关注的重点.为了简化计算，本文假设频谱检测均是理想检测，即是无虚警和漏报并且即刻完成，因此设置Ts＝0.W 是指任一认知用户发起频谱切换请求后系统内没有可用空闲信道的时长，它由授权用户和认知用户行为以及频谱切换机制决定.

延时敏感的系统都有一个延时上限Dmax，当一次频谱切换延时超过此上限，则认为切换超时，把频谱切换超时概率表示为

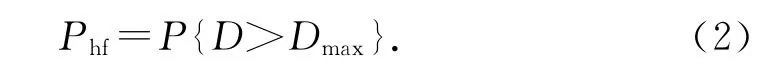
后续章节将会着重推导切换延时的概率分布.

1.2 授权用户行为

系统中总共C个信道，每个信道最多容纳一个授权用户传输数据，系统中存在的授权用户数量用随机变量NPU表示，它在区间［0，C］内变化.如果下一时刻随机变量取值只与该时刻取值相关，则可以用一马氏链来描述这一随机变量，将NPU的状态转移概率写为

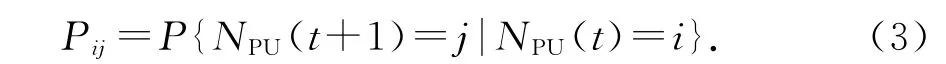
信道里的授权用户数量变化与授权用户的接入方式有关，为了方便分析，假设每个信道中授权用户数量是相互独立且同分布的.单个信道中的授权用户数量为两状态的马氏链，如图2所示，状态0表示该信道中无授权用户，认知用户可以利用该信道进行传输，而状态1则表示授权用户占用了该信道，信道中原有的认知用户需进行频谱切换.可以将式（3）中授权用户总数的转移概率确切地写为

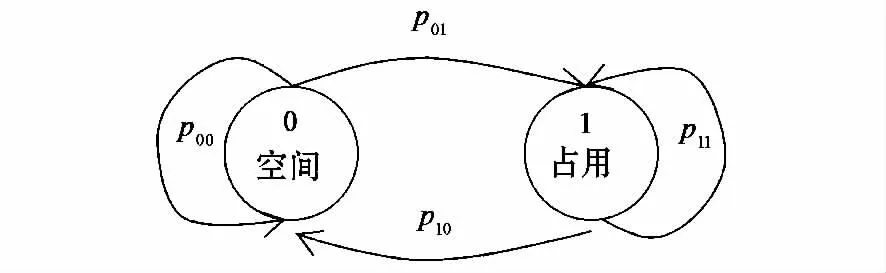
图2 单个信道授权用户状态转移图

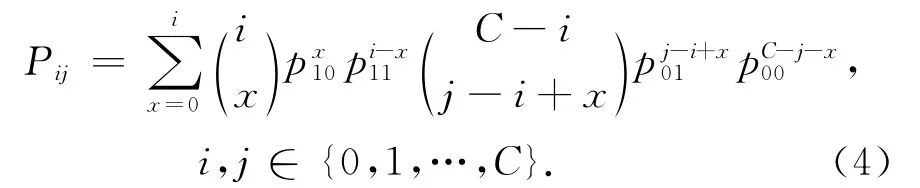
由马氏链理论［12］得到NPU的稳态分布

1.3 认知用户的虚拟排队切换机制

为了分析认知用户数量和频谱切换超时概率的关系，假设系统中始终有M（M≤C）个认知用户在工作.当一个认知用户传输数据的信道被授权用户出现占用时，认知用户发出频谱切换请求，进入缓冲队列等候频谱机会，同一时隙产生的多个请求，则按随机的排序方式进入队列.

与一般的排队模型不同的是，进入请求队列的认知用户并不释放原工作信道供基站统一搜索，而是用如下方式进行：1）处于队列头部的用户可搜索未被其他认知用户登记的共C-M＋1个信道（CM个非认知用户工作信道和头部用户的原工作信道），若寻找到空闲信道则实现频谱切换后退出队列；2）不处于队列头部的认知用户只检测原工作信道是否空闲，如果授权用户结束了传输，则认知用户重返该信道并退出缓冲队列；3）如果队列中用户等待时间超过了延时上限Dmax，则延时清零重新进入队列排队.可以看出，这样的排队模型有多个出口，并不符合单纯的先入先出规则，但只有队列头部用户才有可能通过频谱切换更改自己的工作信道，而非头部用户即使成功返回传输使用的也是同一工作信道，本文将这种机制称为虚拟排队.

由于本文不考虑频谱检测的延时，也就是在出现空闲信道的同时，系统中如果存在请求认知频谱切换的用户，则立刻完成频谱切换.当NPU≤C-M时，切换缓冲队列中不会有认知用户排队，因为新产生的切换请求能够在同一时间完成.所以，任意时刻缓冲队列长度Nh与授权用户数NPU有如下关系为

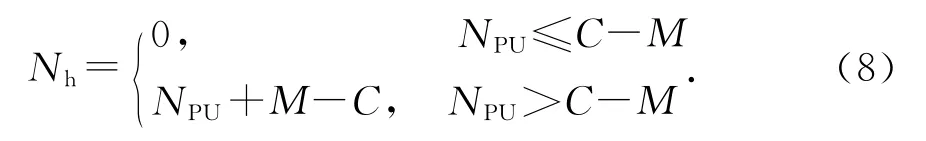
由此可直接得到Nh的稳态分布

2 强制中断率与用户容量

上节描述了虚拟排队切换机制，我们可以将频谱切换延时重新表述为一个认知用户从进入切换缓冲队列到离开队列的时长.以往的文献中没有给出过用户级别切换延时的解析表达.文献［11］虽然得到了延时的概率分布，但只分析了数据包到达速率为常数的认知无线电情景.进入缓冲区的包速率为常数，则可以利用延时状态的无记忆性用马氏链来描述.但本文中缓冲队列用户的到达和离开速率均不为常数，延时的分布也和每个时隙其他认知用户状态变化相关，这样很难找到闭合的数学表达式来计算切换延时的概率.本文采用一种分段近似的方式得到频谱切换延时的概率分布.

2.1 分段近似的频谱切换延时

从一个新发出切换请求的认知用户（下文称为观察用户）的视角出发，观察到缓冲队列中已有Nh0（0≤Nh0≤M-1）个用户，分为两种情况：

1）缓冲队列为空

观察用户进入到队列中，如果该时刻授权用户数小于C-M，观察用户即刻完成频谱切换不产生延时；仅当授权用户数为C-M时，观察用户成为缓冲队列头部，延时等待空闲信道，由此得到缓冲队列为空情况下观察用户产生延时的概率为

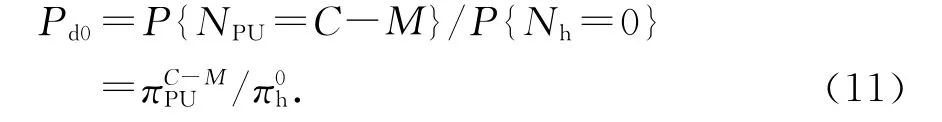
如前所述，作为队列头部用户可以在C-M＋1个信道搜索频谱机会，根据授权用户行为的统计特性，每个时隙搜索到空闲信道完成频谱切换的概率为

则延时Ths的概率分布为

由此可得到频谱切换超时的概率

2）缓冲队列不为空

在观察用户到达以前，缓冲队列中已经有Nh0（0＜Nh0≤M-1）个用户在排队等候频谱切换.从前文可知观察用户完成频谱切换退出队列有两个途径：①观察用户未成为队列头部前就在原信道完成的切换称为重返，记重返延时为TPR；②队列中之前的用户完成频谱切换以后，观察用户成为队列头部进而完成的切换称为转移，记转移延时为TSM.

重返延时的概率分布为转移延时则包含两个部分，一部分是观察用户之前的缓冲用户完成切换的时间记为TNh0；另外就是观察用户成为队列头部后直至完成频谱转移的时间Ths，它有着和式（13）一样的分布.转移延时TSM＝TNh0＋Ths.而观察用户的切换延时则满足

讨论TNh0的分布.从观察用户的角度看，某一时刻队列前方还有k个用户（0＜k≤Nh0），它们是在C-M＋k个信道中搜寻空闲信道，则出现n个空闲信道的概率为

一个时隙内出现空闲信道个数的期望为

这个期望值也就对应着每个时隙观察用户前方队列减少数量的均值，这个值只与前方队列长度k相关.由式（17）和（18）可知前方队列的长度决定了k个用户可搜索资源的数量，前方队列越长，可供搜索的信道越多，λk就越大使队列用户数减少的较快.因此，我们可以将λk看作是前方队列缩短的瞬时速率，而将前方队列长度由k缩短为k-1的过程近似为速率λk的泊松过程，其间经历的时长tk服从均值为λ-1k的指数分布.由于系统是离散时间，将tk的概率分布整理为

式中Fk（t）是参数为λk指数分布的累积分布函数，

因此，TNh0为Nh0段时间的和为

式中，tNh0，tNh0-1，…，t1都是相互独立的，可以推导出TNh0的概率分布为

由此，得到了观察用户频谱切换延时相关的所有分布，进而推出观察用户进入队列时缓冲队列长度为Nh0情况下的切换超时概率

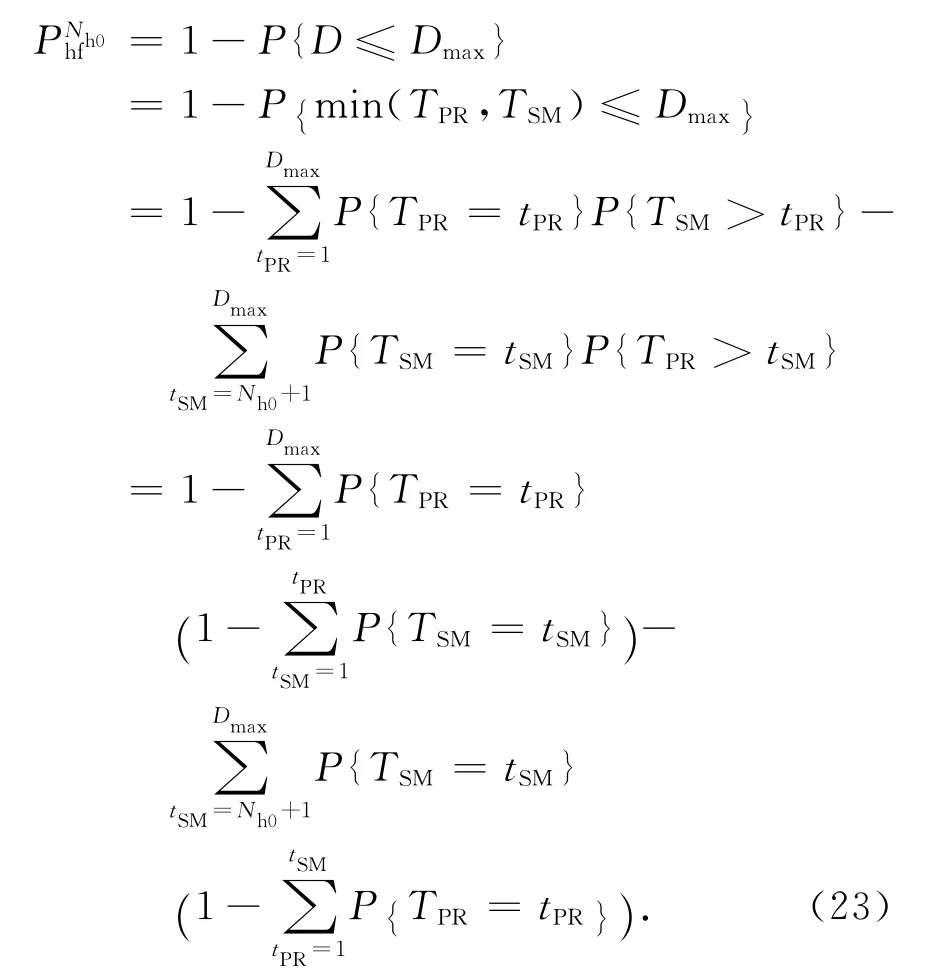
将TPR和 TSM的分布式（13）、（15）和（22）代入式（23）得到结果.

因为PNh0hf是观察用户进入队列时缓冲队列长度为Nh0的条件概率，所以根据全概率公式求得总切换超时概率为

2.2 强制中断率

上节中得到的切换超时率Phf是认知用户产生一次切换请求后超时的概率，而认知用户从进入系统到服务完成可能需要进行多次的频谱切换，一旦发生超时，则服务强制中断.所以，强制中断率不仅和切换超时率有关，还和认知用户发出频谱切换的次数有关.如果将认知用户服务时间的统计特性加入考虑，设任意时隙认知用户传输数据后完成服务的概率为μSU.不受授权用户打断情况下认知用户的服务时长分布为

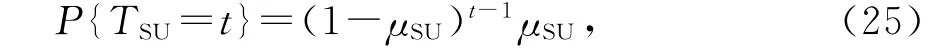
被授权用户打断需要进行频谱切换次数的条件概率为

对TSU进行累加，

认知用户服务过程中发生NSH次频谱切换最终导致强制中断的条件概率为

最终得到强制中断率PFT为

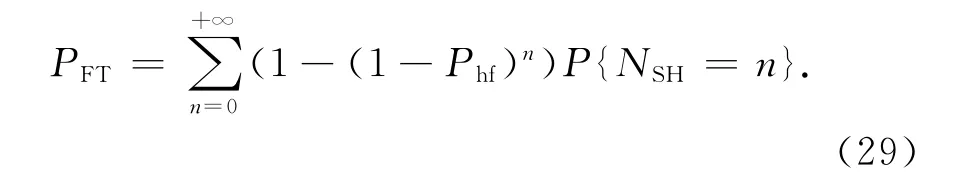
2.3 用户容量

强制中断率是一项重要的QoS标准，有其上限ε的限制.由2.2节中得出PFT的过程可知，强制中断率的取值除了和客观存在的信道条件及授权和认知用户的行为特性有关，更重要的是取决于存在于系统中认知用户的数量.显而易见，越多的认知用户会减少寻找到多余空闲频谱的机会，也就增加了延时，从而导致更多的用户因为超时中断了服务.因此，本文将能够满足强制中断率限制的最大用户数量定义为系统可支持的用户容量，表述如下

获得用户容量参数也有助于进一步地在系统中制定呼叫接入控制等功能.

3 数值结果与仿真

在MATLAB中对本文提出的虚拟排队切换模型和用户容量的结论进行了数值分析与仿真.假设系统中信道数C＝40，采用IEEE802.22标准中对时隙长度的设置为2ms，文献［11］中VoIP服务的延时限制100ms对应Dmax＝50.

选取了四组不同的授权用户行为参数，对应不同的信道条件，利用前文提出的虚拟排队模型，计算得到认知用户数量与频谱切换超时率的关系.从图3可以看出，当切换超时率小于10-1数量级时，理论推导结果和仿真数值能很好的吻合.当超时率继续增大时，理论所得和仿真值的差距变大，这是由于虚拟排队模型中用户切换超时后会退出队列重新发起切换请求，但在分段近似计算过程中，没有将超时概率近似为用户退出队列速度的一部分，只考虑了用户通过频谱切换途径退出队列的速度，队列头部超时后继续处于头部寻找频谱机会从而增加了队列后方用户超时的概率.但过大的切换超时概率造成的强制中断率是不能被系统接受的，因此在切换超时率较小的条件下利用本文提出的模型分析系统性能是准确的.

图3 认知用户数对频谱切换超时概率的影响

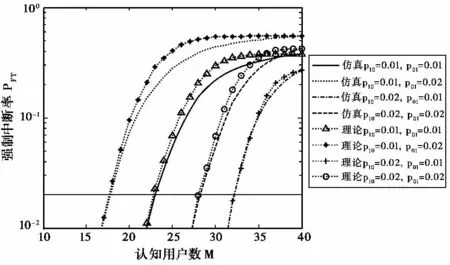
图4 认知用户数与强制中断率的关系（μSU＝0.01）

从图3中的参数对比可看到，同样p10（0.01或0.02）参数的两组超时概率取值有着一样的上限.容易理解的是当认知用户数同信道数相同时，没有多余的信道可供频谱转移，所以，切换延时服从式（15）的分布，这个上限也就仅由p10决定而与标志着授权用户到达间隔时间的参数p01无关.第一组（p10＝0.01，p01＝0.01）和第四组（p10＝0.02，p01＝0.02）的信道空闲稳态概率pI都为0.5，但第四组中的参数表明授权用户更快的转变状态，因此缩短了认知用户寻找信道的时间.

设定μSU＝0.01，得到认知用户数与强制中断率的关系，如图4所示.图4中标出了强制中断率的限制ε＝0.02，很容易得到不同信道条件下的用户容量.理论分析数值和仿真结果也能够很好的吻合.

4 结 论

认知系统中授权用户拥有更高优先级，为了分析授权用户行为如何对认知用户的频谱切换产生影响，本文从切换延时的角度出发，提出了新的虚拟排队切换模型对其进行理论推导；并利用了分段近似的方法得到了强制中断率和用户容量的解析解，这一结论在切换超时率较小的情况下是成立的.仿真与数值分析的结果也证实了本文模型的有效性.获得的用户容量参数可以为进一步的呼叫接入控制提供支持.

［1］MITOLA J，MAGUIRE G Q.Cognitive radio：making software radios more personal［J］.IEEE Personal Communications，1999，6（4）：13-18.

［2］HAYKIN S S，MOHER M.Modern Wireless Communications［M］.Pearson Prentice Hall，2005.

［3］ZHAO Q，KRISHNAMACHARI B，LIU K Q.On myopic Sensing for multi-channel opportunistic access：structure，optimality，and performance［J］.IEEE Transactions on Wireless Communications，2008，7（12）：5431-5440.

［4］KIM H，SHIN K G.Efficient discovery of spectrum opportunities with MAC-layer sensing in cognitive radio networks［J］.IEEE Transactions on Mobile Computing，2008，7（5）：533-545.

［5］YOON S U.Voluntary spectrum handoff：a novel approach to spectrum management in CRNs［C］//2010 IEEE International Conference on Communications（ICC）.Cape Town，2010：1-5.

［6］WANG C W，WANG L C，ADACHI F.Modeling and analysis of multi-user spectrum selection schemes in cognitive radio networks［C］//IEEE 20th International Symposium on Personal，Indoor and Mobile Radio Communications.Tokyo，2009：828-832.

［7］WANG L C，WANG C W.Spectrum management techniques with QoS provisioning in cognitive radio networks［C］//5th IEEE International Symposium on Wireless Pervasive Computing （ISWPC）.Modena，2010：116-121.

［8］WANG L C，WANG C W，FENG K T.A queueing theoretical framework for QoS-enhanced spectrum management in cognitive radio networks［J］.IEEE Wireless Communications，2011，18（6）：18-26.

［9］王 玲，彭启琮，彭启航.基于收益的认知无线电多信道阶梯排队接入机制分析［J］.电子与信息学报，2012，34（8）：1944-1949.WANG Ling，PENG Qicong，PENG Qihang.Reward based multichannel step queuing access scheme in cognitive radio［J］.Journal of Electronics Information Technology，2012，34（8）：1944-1949.（in Chinese）

［10］LEE H.Capacity improvement and analysis of VoIP service in a cognitive radio system［J］.IEEE Transactions on Vehicular Technology，2010，59（4）：1646-1651.

［11］GUNAWARDENA S.Voice capacity of cognitive radio networks for both centralized and distributed channel access control［C］//IEEE Global Telecommunications Conference（GLOBECOM）.Miami，2010：1-5.

［12］COOPER R B.Introduction to Queueing Theory［M］.2nd ed.New York：Elsevier North Holland，1981..