双向抛物方程的并行方法研究

张青洪 廖 成 盛 楠 陈伶璐

（西南交通大学电磁场与微波技术研究所，四川 成都610031）

引 言

随着电磁波理论的迅速发展，基于电磁波技术的产品和设备被普遍应用于无线通信、电子对抗、雷达等诸多领域［1-3］，复杂环境与电波干扰等会对无线电系统的性能造成显著影响，因此，准确求解复杂环境中电磁波的传播特性具有重要的现实意义.

抛物方程方法（Parabolic equation，PE）最早由Leontovich和Fock［4］在20世纪40年代提出，它不仅可以处理不规则地形和不同电磁参数的地表结构对电波传播的影响，还能同时计算出复杂大气结构对电波传播所产生的折射效应，因此被广泛应用于预测和分析电磁波的传播特性［5-9］.传统的PE忽略了波的后向传播，当地表存在各种不规则的障碍物时，算法会带来较大误差，而双向抛物方程考虑了波的后向散射，其计算结果更准确［10-12］，因此，对双向抛物方程方法进行研究十分必要.

近年来，国内外学者对双向抛物方程展开了初步研究，如Ozgun等［13］用双向抛物方程模拟了大气波导环境下多刃峰及不规则地形环境中电磁波的总场分布，李德鑫等［14］提出了基于前-后向混合差分方法的递归双向抛物方程模型，并仿真分析了单刃峰和实际地形中的电波传播特性.目前处理多障碍物间的多次反射时，均是采用串行计算来完成，在大尺度传播环境中，障碍物间多次反射波的数量会显著增加，此时双向抛物方程计算所需的时间也将大大增加，而在电子战、指挥自动化等实际应用中，实时而准确地预测空间电磁特性具有至关重要的意义.为此，本文提出了基于OpenMP的双向抛物方程并行方法，并给出了具体的实现方案，通过与串行计算进行对比分析，验证了并行方法的正确性和高效性.

1 双向抛物方程模型

双向抛物方程模型是在传统前向抛物方程的基础上，引入后向抛物方程来计算电磁波的后向传播场，通过将各后向传播场累加至前向场，从而获得计算区域的电磁波总场分布.前向传播场可以通过传统抛物方程来计算，下边将介绍后向传播场的求解方法.

设电磁场时谐因子为e-iωt，在直角坐标系（x，y，z）下，由二维标量波动方程［15］可以推导出宽角型后向抛物方程

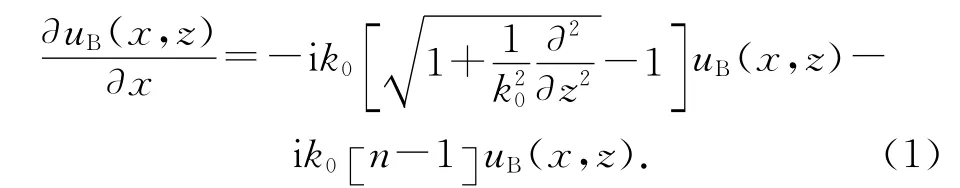
式中：n为媒质的折射率；k0为真空中的传播常数；uB（x，z）为沿x轴负向传播场的波函数.后向抛物方程分步傅里叶（Split-Step Fourier Transform，SSFT）解的形式为

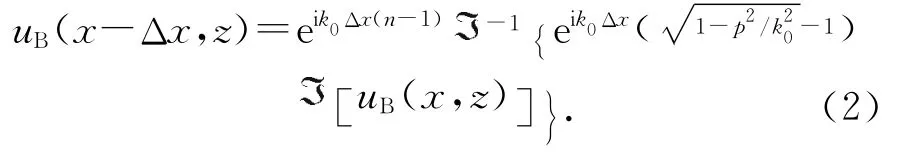
由后向抛物方程SSFT解的形式可知，其与前向抛物方程解的形式一致，只是传播常数和步长相差一个符号，因此在步进求解后向抛物方程时，只需将前向抛物方程中的传播常数和步长取相反数即可，其它过程不变.后向抛物方程初始场可以通过前向传播场和地形边界条件来求解.

在处理不规则地形时，将地形视为一系列刃峰组合，如图1所示，以相邻刃峰高度相差的数据点作为反射点，如图中“■”所示，用该处的反射场作为后向抛物方程的初始值，分别计算各刃峰处的反射场，总反射场为各刃峰后向反射场的累加，“●”为不同传播模式下的电波传播总场，“○”代表场的大小为0.

图1 不规则地形前向-后向传播

以x＝x0处的地形为例（如图1（b）假设h0为此处刃峰的高度，由切线上总场为零可求得后向抛物方程初始场的计算公式为

得到后向抛物方程的初始值后就可以通过其SSFT解法求解空间电磁波的后向场，进而求得空间总场的分布.对于x＝x0处的地形刃峰，在x＞x0的区域内仅有电波前向场，而x＜x0区域则为前向场和后向场的叠加，因此空间电磁波总场的计算公式为

若电波传播区域的地形为孤立的单调函数，地形的后向反射波不会被其它地形反射，当反射场运算至发射源或计算区域最大距离处时，算法结束；若电波传播区域存在多个不规则地形，则需要考虑地形间的多次反射波.以双刃峰环境为例，当第二个刃峰反射的后向场到达第一个刃峰时，被再次反射且沿前向步进，如此循环，电磁波在二刃峰间被多次反射，当达到一定的收敛条件后，算法终止，空间电波传播的总场为各前向传播场和后向传播场的总和.一般设定多次反射计算终止的条件为总场满足

式中：ψm-1和ψm分别为第m-1次和第m次反射后的总场；ε是指定的阈值，本文取0.01；· 为矢量的模值.

2 双向抛物方程并行方案

OpenMP是一个为在共享存储的多处理机［16］上编写并行程序而设计的应用编程接口，能够支持并行计算时对线程和变量的灵活设计和控制，具有简单、移植性好和可扩展等优点.OpenMP采用FORK-JOIN并行执行模式，主线程串行执行，当遇到派生点后，主线程创建出并行线程执行并行任务，直到算法结束，并行线程挂起或退出，如图2所示.本文将基于Open-MP实现双向抛物方程的并行算法.

图2 OpenMP并行执行模式

双向抛物方程计算空间总场时，先应用前向抛物方程计算电磁波的前向场，再将各障碍物的多次反射场叠加到前向场中，进而求得空间的总场分布.由于二个障碍物间后一次反射的初始值必须通过前一次反射场来计算，因此对于二障碍物间的多次反射不能通过并行计算来实现，而对于每二个障碍物间的反射，则可以分配到不同的线程来并行计算，以减少双向抛物方程总的计算时间.

通过上述分析，本文确定双向抛物方程的并行方案如图3所示，即先通过主线程计算得到空间的前向场，再通过OpenMP将各障碍物对间的多次反射分配到各子线程来计算，最后将求得到的各反射场叠加到前向场进而求得空间的总场分布.

图3 双向抛物方程并行方案

3 数值算例

3.1 双刃峰环境

假设发射天线高5m，频率为3GHz，水平极化波，天线方向图为高斯方向图函数，其能量3dB宽度为3°；地面为理想导电平面，大气环境为理想均匀大气；刃峰距离源的位置分别为20km，40km，高度分别为100m，150m.本文所有仿真的平台均为具有16个计算核心的服务器.

图4给出了电波传播35km时不同高度上的传播因子（Propagation Factor，PF），并将并行双向抛物方程方法与串行双向抛物方程及射线跟踪法的仿真结果进行对比.

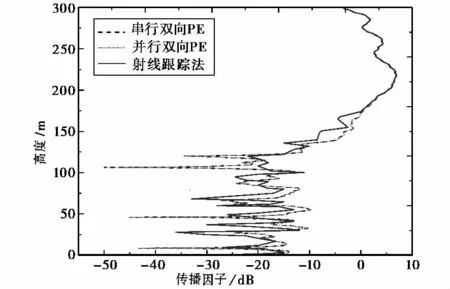
图4 电波传播35km时不同高度上的传播因子

由图4可以看出：并行双向抛物方程与串行双向抛物方程仿真结果完全一致，且与射线跟踪法的结果吻合很好，由此验证了并行双向抛物方程的正确性和有效性.

3.2 十五刃峰环境

并行程序的性能可由加速比来衡量，定义加速比为

式中：t1为串行求解所需时间；tN为N个线程并行求解所需时间.

本算例中源参数设置与双刃峰相同，假设地面为中等干燥地面，大气环境为表面波导，其大气折射率分布如图5所示.刃峰距离源的位置分别为10、25、40、50、65、70、80、95、105、120、140、155、170、180、195 km，刃峰高度分别为50、100、75、50、50、100、75、125、100、75、50、50、100、75、125m.

图5 表面波导修正折射率分布图

从图6和图7可以看出：随着线程数的增加抛物方程的计算时间逐渐减少，加速比逐渐增加，在线程数到达15时，并行双向抛物方程的计算时间为42.125s，相对于串行双向抛物方程减少了88.7%，计算速度得到大幅度提高，且此时加速比为8.8，加速效果很好.可见，采用并行方法后，有效地解决了双向抛物方程计算时间过长的问题.

图6 不同线程数的计算时间对比图

图7 不同线程数的加速比对比图

图8和图9分别是计算环境存在不同刃峰数量K时串行双向抛物方程及并行双向抛物方程的计算时间和加速比.

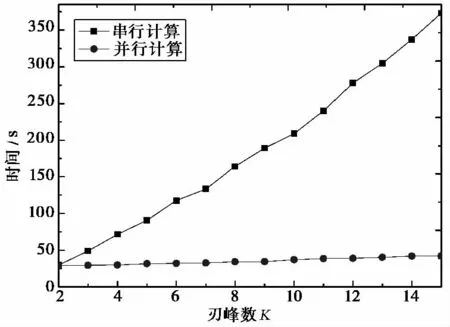
图8 不同刃峰数时串行和并行计算对比图

图9 不同刃峰数的加速比对比图

由图8可知：随着刃峰数的增加，串行双向抛物方程的计算时间几乎呈线性增长，而并行双向抛物方程的计算时间则变化不大，随着刃峰数量的增加，刃峰间的多次反射数量也会增加，进而导致串行双向抛物方程的计算时间也随之增加，而由于刃峰数小于最大线程数，增加的刃峰对间的多次反射被分配到空闲的线程并行执行，因此并行双向抛物方程的计算时间变化很小；在图9中：由于随着刃峰数的增加，参与并行计算的线程也随之增多，加速比也因此增加.可见，随着计算区域中障碍物数量的增加，并行双向抛物方程的加速效果也会更好.

3.3 实际地形

实际地形中，仿真预测了一中国移动GSM基站天线的电磁覆盖特性.假设基站位于N81°01′14″E36°16′54″处，选取基站至 N81°35′86″E36°25′74″的山区二维地形剖面作为仿真的地形数据，地面为中等干燥地面；设基站发射天线距离地面高度为55 m，频率为0.9GHz，垂直极化，天线垂直方向的半功率角为8°；大气采用标准大气环境，水平步长取为31.863m.

图10和图11分别给出了实际地形中前向抛物方程和并行双向抛物方程传播因子空间伪彩图，表格1列出了串、并行双向抛物方程计算性能的对比.

图10 前向抛物方程传播因子空间伪彩图

图11 并行双向抛物方程传播因子空间伪彩图

表1 并行双向抛物方程计算性能对比

由图10和图11可知：前向抛物方程没有考虑波的后向传播，因此在地形后方电磁波衰减很大，此时该区域没有基站信号覆盖，而双向抛物方程能够体现出各不规则地形对电磁波的后向反射，尤其在第一个和第二个山峰之间，反射波较大，基站天线在此处信号较好，其结果更加符合现实物理规律.在本算例中，并行计算的线程数为4，由表1可知：相对于串行计算，并行双向抛物方程的计算时间下降60.75%，加速比为2.55，这表明在实际应用中，并行方法能够有效地减少双向抛物方程计算的时间，起到了很好的加速效果，具有高效性.随着实际应用中地形数量的增加，并行双向抛物方程的加速效果将会更加明显.

4 结 论

双向抛物方程在求解大尺度、多障碍物环境中的电波传播特性时，计算时间会急剧增加，针对这一问题，本文提出了基于OpenMP的双向抛物方程并行方法.通过与串行双向抛物方程的对比可知，并行方法能够极大地减少计算时间，具有很好的加速效果.最后，本文以 N81°01′14″E36°16′54″至 N81°35′86″E36°25′74″间一GSM基站天线电磁覆盖特性的计算为例，展示了并行双向抛物方程在处理复杂地形中电波传播问题的高效性，表明该方法适用于实际多障碍物场景中电波传播特性的模拟和分析.

［1］蒋晓红，吕东强，肖 斌.认知无线电在山区无线通信中的应用研究［J］.无线电通信技术，2010，36（6）：55-57＋61.JIANG Xiaohong，LÜDongqiang，XIAO Bin.Investigation on cognitive radio to wireless communication in mountain area［J］.Radio Communications Technology，2010，36（6）：55-57＋61.（in Chinese）

［2］李大勇，叶琼龙.无人机在舰载电子对抗系统中的应用［J］.电子对抗技术，2004，19（1）：38-39＋46.LI Dayong，YE Qionglong.application of the pilotless aircraft in naval EW system［J］.Electronic Information Warfare Technology，2004，19（1）：38-39＋46.（in Chinese）

［3］朱 勇.直升机载预警雷达试验系统［J］.合肥学院学报：自然科学版，2008，18（3）：47-51.ZHU Yong.The test system of helicopter-borne surveillance radar［J］.Journal of Hefei Uni-versity（Natural Sciences Edition），2008，18（3）：47-51.（in Chinese）

［4］LEONTOVICH M A，FOCK V A.Solution of propagation of electromagnetic waves along the earth’s sur-face by the method of parabolic equation ［J］.J Phys USSR，1946，10（1）：13-23.

［5］JANASWAMY R.Path loss predictions in the presence of buildings on flat terrain：A 3-D vector parabolic equation approach［J］.IEEE Trans on AP，2003，51（8）：1716-1728.

［6］LI Dexin，ZHAO Xiuli，SHANG Yongshuang.Prediction of radio wave propagation over irregular terrain by the improved DMFT algorithm［C］∥Cross Strait Quad-Regional Radio Science and Wireless Technology Conference（CSQRWC），2011，1：75-78.

［7］郭建炎，王剑莹，龙云亮.森林中电波传播的抛物方程法［J］.电波科学学报，2008，22（6）：1042-1046.GUO Jianyan，WANG Jianying，LONG Yunliang.Parabolic equation model for wave propagation in forest environments［J］.Chinese Journal of Radio Science，2008，22（6）：1042-1046.（in Chinese）

［8］李广成，郭立新，吴振森，等.障碍物对蒸发波导中电波传播影响研究［J］.电波科学学报，2011，26（4）：621-627.LI Guangcheng，GUO Lixin，WU Zhensen，et al.Influence of obstacle towards electromagnetic wave propagation in the evaporation duct［J］.Chinese Journal of Radio Science，2011，26（4）：621-627.（in Chinese）

［9］来嘉哲，方广有，刘帅.战场电磁环境构建中的抛物方程应用研究［J］.雷达学报，2012，1（1）：63-68.LAI Jiazhe，FANG Guangyou，Liu Shuai.Research on constructing war-field electromagnetic environment using parabolic equation［J］.Journal of Radars，2012，1（1）：63-68.（in Chinese）

［10］ORAIZI H，HOSSEINZADEH S.Radio-wave-propagation modeling in the presence of multiple knife edges by the bidirectional parabolic-equation method［J］.IEEE Trans Vehicular Technology，2007，56（3）：1033-040.

［11］王 昆，杨永钦，龙云亮，等.多刃峰环境无线电波传播预测的双向抛物方程法［J］.电波科学学报，2011，26（6）：1058-1064＋1228.WANG Kun，YANG Yongqin，LONG Yunliang.Twoway parabolic equation approach for modeling radio wave propagation in the presence of multiple knife edges［J］.Chinese Journal of Radio Science，2011，26（6）：1058-1064＋1228.（in Chinese）

［12］WANG K，LONG Y.Propagation modeling over irregular terrain by the improved two-way parabolic equation method［J］.IEEE Trans on AP，2012，60（9）：4467-4471.

［13］OZGUN O.Recursive two-way parabolic equation approach for modeling terrain effects in tropospheric propagation［J］.IEEE Trans on AP.，2009，57（9）：2706-2714.

［14］李德鑫，杨日杰，官 巍，等.不规则地形条件下的双向抛物方程模型研究［J］.宇航学报，2012，33（2）：235-241.LI Dexin，YANG Rijie，GUAN Wei，et al.Research on two-way parabolic equation modeling under irregular terrain environment［J］.Journal of Astronautics，2012，33（2）：235-241.（in Chinese）

［15］LEVY M.Parabolic Equation Methods for Electromagnetic Wave Propagation［M］.London：IEEE，2000.

［16］陈国良.并行算法实践［M］.北京：高等教育出版社：2004.CHEN Guoliang.Practice of Parallel Algorithm［M］.Beijing：Higher Education Press，2004.（in Chinese）