前向雷达目标回波成分与特性分析
赵晓彤,郭琨毅,盛新庆,屈泉酉
(北京理工大学信息与电子学院电磁仿真中心,北京 100081)
前向雷达目标回波成分与特性分析
赵晓彤,郭琨毅,盛新庆,屈泉酉
(北京理工大学信息与电子学院电磁仿真中心,北京 100081)
一般认为双基地雷达在前向散射区(双基地角为135°~180°)的RCS较其他方向更大,前向雷达的应用正是建立在此优势的基础上。然而某些实际场景下天线所接收的电磁波并非散射波,而是散射波与发射天线辐射波的复矢量叠加。由于相位和电磁场极化方向的差异,总场表现出与散射场不同的变化特性。用全波法计算了扩展目标分别在近场、远场观测条件下前向区散射场、总场随距离和方位的变化,分析和总结了总场与散射场的数值特性差异。
双基地; 前向; 散射特性; 全波法
0 引 言
前向散射雷达是指工作在前向散射区的双基地雷达[1]。前向散射雷达相较于其他的雷达有以下特点[2]:当目标靠近基线,即雷达发射机和接收机之间的连线时,雷达截面积(radar cross section,RCS)会有大幅度上升。相较于单基地雷达,前向雷达截面积可增大20~40 dB;由于前向散射的特点,测得目标的远场RCS在高频区受目标的吸波涂层的影响很小。这些优势使前向散射雷达可以解决传统的单站雷达难以解决的问题,例如小型低空目标、隐身目标的探测。近年来,前向雷达的功能得到了很大的开发,在目标检测、跟踪与目标识别[1,3-8]雷达目标成像[9-11]等方面,前向散射雷达都有很广泛的应用;由于自身体制原因带来的杂波,文献[12-13]进行了建模与分析。
实际前向雷达所接收的回波信号的成分可能会包含发射天线直达波的影响,如对于宽波束雷达,在较宽的接收角度范围内,雷达接收的回波信号是总场,即散射电磁场与入射电磁场的复矢量叠加结果。由于相位和电磁场极化方向的差异,总场表现出与散射场不同的变化特性。
目前,前向散射一般采用阴影理论进行近似计算[14]。然阴影理论仅在远场条件下、光学区散射、正前向很小的角度范围内有效,其他情况下的计算结果会与实际结果相去甚远。因此,采用阴影理论近似计算结果研究前向雷达回波特性会存在问题。鉴于此,本文采用全波法-合元极技术(FE-BI-MLFMA)[15],计算了扩展目标在远场和近场观条件下的散射场和总场,分析了各成分随方位角、距离、双基地角、极化等参数改变的规律,总结了散射场和总场的变化特性差异。
1 前向雷达接收回波的计算
前向雷达与目标的几何位置关系如图1所示,其中发射天线为非窄波束天线[2]。当波束宽度较大时,在很大的双站角范围内,接收雷达处于总场接收区,此时入射波会对接收回波信号造成干扰。
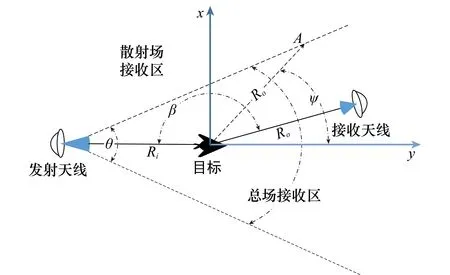
图1 前向雷达几何结构示意图Fig.1 Geometry of FSR

前向散射场的近似计算多基于阴影理论。该理论首先用巴比涅简化原问题,得到更简单却等效的问题。巴比涅原理的等效过程为:首先用与目标轮廓形状相同的不透明平板代替目标,然后再用一块无限大的互补屏(其空隙与平板相同)代替平板。由巴比涅原理可知,原目标的散射问题与无限大缝隙平板的散射问题(其缝隙与目标轮廓形状完全相同)等效。于是,对于不透明空隙平板,利用惠更斯原理计算其前向散射场[16],进而得到目标的双站RCS为
(7)
式(7)的积分作用在与目标投影轮廓相同的缝隙上。其中,λ为波长;k为散射场波数矢量;ρ为孔径平面内任一点的径向矢量;A为孔径面。双基地角为180°时,式(7)就简化为
(8)
该近似方法存在明显的局限性:该方法将立体目标直接等效为平板目标的近似很不严格;目标尺寸需远远大于自由空间波长;计算散射场时没有考虑极化问题;目标相对于发设计和接收机都处在远场范围内,即,R≥2D2/λ,其中R为目标与接收机(发射机)之间的距离,D为目标的最大尺度。
因此,当目标为扩展目标,其散射成分包括非光学散射贡献,且雷达处于目标散射的非远场区时,采用近似法计算目标的前向RCS会存在难以估计的误差,为了保证计算精度采用全波法计算。
为了说明近似法的误差,下文给出了某隐身飞机的远场双基地RCS计算结果。基于前向近似理论的近似法与全波法的计算结果如图2所示。入射方向为机头方向;入射频率为1.3 GHz;接收方向为xoy平面的前向散射区;全波法的极化方式为VV极化。由图可见,即使满足远场条件下,仅在β=180°±1.5°的较小范围内近似法与全波法的计算结果相吻合,误差小于3 dB,而其他角度下存在很大误差,双站角为181.8°时,误差约为15 dB。

图2 全波法与近似法的双基地RCS计算结果对比Fig.2 RCS comparison of different methods
2 典型目标的前向雷达回波计算
本文以3种典型扩展目标为例,详细计算了在不同入射距离、接收距离和方位处的入射场、目标散射场、总场的结果。3个目标分别为圆锥和两种不同的飞机,这3种目标对于空中飞行目标具有一定的代表性。目标的尺寸参数如表1,数值算例共有3组,具体的计算参数设置见表2。

表1 目标的尺寸参数

表2 目标的计算参数

图3 目标几何位置示意图Fig.3 Geometry of the targets
2.1远场入射、接收及接收方位变化
入射和接收距离满足远场条件,3个目标的散射场和总场幅度随双站角β变化的情况,如图4~图6所示。
图4展示了圆锥目标在前向散射区(双站角在180°±45°之间)的入射场、散射场和总场幅度的大小关系。由图4可见,散射场幅度仅仅在β=180°的正前向很大,约为2.43 V/m,稍稍偏离便迅速减小,如偏离2°则衰减为β=180°时幅度的1/10;由于散射场与入射场的复矢量叠加效果,总场幅度在β=180°±3°范围内剧烈振荡,幅度达4 dBV/m,始终大于散射场幅度。图5和图6为飞机目标在前向散射区散射场和总场幅度随双站角变化图。与圆锥类似,散射场幅度仅仅在β=180°很大,稍稍偏离则迅速减小:图5在β=180°+6°时减小为1/6,图6在β=180°±7°时减小为1/7;总场曲线振荡区域更宽,例如图6总场振荡的幅度达7 dBV/m,并且总场幅度大于散射场幅度。
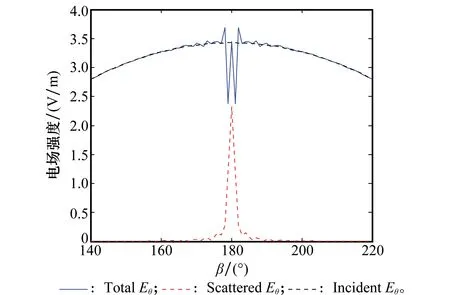
图4 圆锥的散射场总场幅度随β变化Fig.4 Comparison of electric field scattered by the cone between different components

图5 民用飞机的散射场和总场幅度随β变化Fig.5 Comparison of electric field scattered by the plane between different components

图6 隐身飞机的散射场和总场幅度随β变化Fig.6 Comparison of electric field scattered by X22 between different components
2.2近场入射,接收距离由近及远变化
在近场入射条件下,3个目标的散射场和总场幅度随接收距离的变化,如图7~图9所示。

图7 圆锥在近场入射下的前向散射场和总场幅度随Rr变化Fig.7 Comparison of electric field scattered by the cone under near field incidence between different components
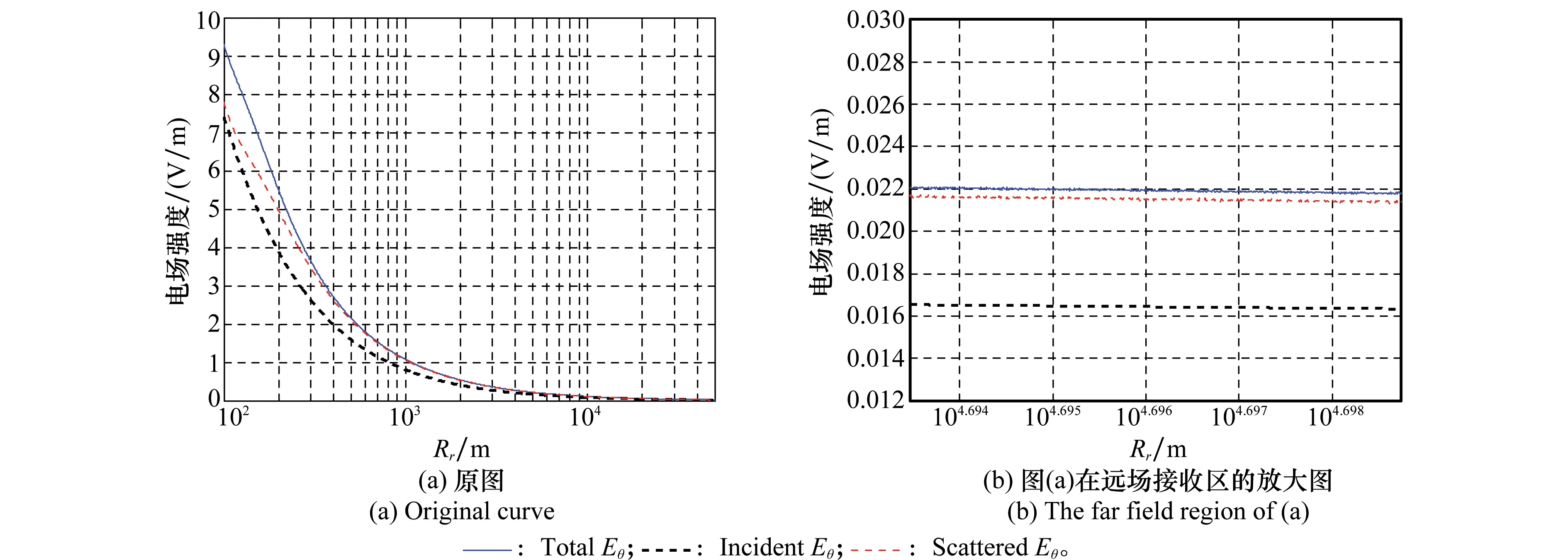
图8 民用飞机近场入射的前向散射场和总场幅度随Rr变化Fig.8 Comparison of electric field scattered by the plane under near field incidence between different components

图9 隐身飞机近场入射的前向散射场和总场幅度随Rr变化Fig.9 Comparison of electric field scattered by X22 under near field incidence between different components
图7可见,圆锥在接收距离Rr<0.4 km的非远场接收区,散射场幅度有很大振荡,总场也随之振荡;在逐渐进入远场接收区后,散射场和总场幅度大小趋于稳定,总场大于散射场。经计算,在远场区(Rr=1 km),散射场和总场的RCS分别为-13.8 dB、-5.7 dB,差别约为7.9 dB。图8可见,民用飞机目标总场幅度大于散射场幅度,在远场区(Rr=50 km),散射场和总场的RCS分别为33.4 dB、38.2 dB,相差4.4 dB。由图9所示,隐形飞机目标与其他目标不同,散射场幅度大于总场幅度,散射场和总场的RCS分别为33.5 dB、36.8 dB,相差3.3 dB。
2.3远场入射,接收距离由近及远变化
在远场入射条件下,3种目标的的散射场和总场幅度随接收距离的变化,如图10~图12所示。

图10 圆锥远场入射的前向散射场和总场幅度随Rr变化Fig.10 Comparison of electric field scattered by the cone under far field incidence between different components

图11 民用飞机远场入射前向散射场入射场和总场幅度随Rr变化Fig.11 Comparison of electric field scattered by the plane under far field incidence between different components

图12 隐身飞机远场入射的前向散射场和总场幅度随Rr变化Fig.12 Comparison of electric field scattered by X22 under far field incidence between different components
从图10 (a)可以看出,在近场接收区,散射场幅度振荡起伏很大,进而造成总场的起伏振荡。由图10 (b)可以观察到,在远场接收区(Rr=1 km),散射场和总场幅度的振荡趋于平稳。经计算,散射场和总场的RCS分别为46.8 dB、53.0 dB,差别约为6.2 dB。由图11和图12可见,在逐渐进入远场接收区,两种飞机目标的总场和散射场曲线趋于稳定,总场幅度大于散射场。民用飞机的散射场和总场的RCS分别为44.1 dB、53.8 dB,差别约为9.7 dB。在远场接收区(Rr=50 km),隐身飞机的散射场和总场的RCS分别为41.5 dB、52.1 dB,差别约为10.6dB;综上,在远场入射远场接收的条件下,前向散射场和总场求出的RCS值相差在6dB以上。三目标在近、远场条件下、正前向和偏离正前向3度时,总场与散射场的RCS数值差异,见表3所示。可见,总场与散射场的差异程度随距离和方位而剧烈变化,当总场中散射分量很小时,显然会造成雷达回波有效信号分离的困难。

表3 不同情况下总场与散射场RCS差值
3 结 论
本文采用矩量法,以3个典型扩展目标为例,计算与分析了近、远场条件下目标前向散射区总场与散射场数据,并得到一些有意义的结论,对前向雷达的应用具有一定的参考价值。
虽然前向散射区为β=180°±45°以内的很大角度,然而由弹头类目标、民航飞机、隐身飞机的散射场幅度随接收角度变化的结果可知,散射场仅仅在正前向附近非常小的角度内较大,偏离此范围则急剧下降,而且不同目标的前向散射效应的角度范围也不同:圆锥目标的角度范围为3°,民用飞机目标的角度范围为13°,隐身飞机目标的角度范围为11°。因此,前向雷达是否可以获得比单站雷达更强目标散射信号,需要先对具体目标散射方位特性预先计算。
由三目标的前向散射场幅度随接收距离的变化结果来看,在近场接收区总场与散射场幅度随接收距离剧烈振荡,而且两者的振荡特性存在明显差异。可见,在非远场条件下散射场和总场的差异随具体目标而异,无统一性的规律。总场幅度甚至为弱于散射场幅度,这会对分离雷达回波的有效信号造成困难。
依据远场入射和接收条件下三目标散射场和总场RCS定量计算结果可知:正前向观测时,圆锥的散射场比总场小约为6.2 dB;民用飞机的散射场比总场小约9.7 dB。隐身飞机的散射场比总场小约10.6 dB。当偏离正前向3°时,三目标的散射场和总场RCS差别则变为25.3 dB,13.2 dB,15.4 dB。可见总场与散射场的差异随双站角而剧烈变化,很多情况下相差会达10 dB以上。当总场中散射场幅度分量越小,造成分离雷达回波的有效信号的困难越大,特别对于低、小、慢目标,此问题更为严重。
[1] Wang H J.The disquisition of targets tracking in the bistatic forward scattering radar[D].Xian:Xidian University,2009.(王辉军.双基地前向散射雷达目标跟踪研究[D].西安:西安电子科技大学,2009.)
[2] Blyakhman A B,Runova I A.Forward sattering radiolocation bistatic RCS and target detection[C]//Proc.of the IEEE Radar Conference,1999:20-22.
[3] Cherniakov M,Abdullah R S,Jancovic A R,et al.Automatic ground target classification using forward scattering radar[J].IEE Radar,Sonar and Navigation,2006,153(5):427-437.
[4] Chen X L,Hu C,Zeng T.Automatic vehicle classification based on forward scattering radar[J].Science in China,Series F:Information Sciences,2012(11):1471-1480.(陈新亮,胡程,曾涛.一种基于前向散射雷达的车辆目标自动识别方法[J].中国科学(信息科学),2012(11):1471-1480.)
[5] Blyakhman A B,Myakinkov A V,Ryndyk A G.Measurement of target coordinates in three-dimensional bistatic forward-scattering radar[J].Journal of Communications Technology and Electronics,2006,51(4):397-402.
[6] Suberviola I,Mayordomo I,Mendizabal J.Experimental results of air target detection with a GPS forward-scattering radar[J].IEEE Trans.on Geoscience and Remote Sensing Letters,2012,9(1):47-51.
[7] Gashinova M,Daniel L,Sizov V,et al.Phenomenology of Doppler forward scatter radar for surface targets observation[J].IEE Radar,Sonar and Navigation,2013,7(4):422-432.
[8] Kovalev A N,Kovalev F N.Determination of the difference of the distances to a moving object in the forward-scatter radar systems with diversity reception[J].Radiophysics and Quantum Electronics,2014,57(6):441-445.
[9] Cao Y H,Zhang T,Luo B F.Experimental imaging results for forward scattering hedge radar[J].Modem Radar,2009,31(1):18-20.(曹运合,张涛,罗斌凤,等.前向散射雷达目标成像实验研究[J].现代雷达,2009,31(1):18-20.)
[10] Cheng H,Xiao L L,Teng L.An accurate SISAR imaging method of ground moving target in forward scatter radar[J].Science in China,Series F:Information Sciences,2012(55):2269-2280.
[11] Cheng H,Chao Z,Tao Z,et al.Radio holography signal reconstruction and shadow inverse synthetic aperture radar imaging in ground-based forward scatter radar:theory and experimental results[J].IEE Radar,Sonar and Navigation,2014,8(8):907-916.
[12] Hu C,Liu C J,Zeng T,Statistical analysis and simulation method of forward scattering clutter in bistatic radar[J].Journal of Signal Processing,2013(3):293-303.(胡程,刘长江,曾涛,等.双基地前向散射雷达杂波分析与模拟方法[J].信号处理,2013(3):293-303.)
[13] Gashinova M,Kabakchiev K,Daniel L,et al.Measured forward-scatter sea clutter at near-zero grazing angle:analysis of spectral and statistical properties[J].IEE Radar,Sonar and Navigation,2014,8(2):132-141.
[14] Glaser J I.Bistatic RCS of complex objects near forward scatter[J].IEEE Trans.on Aerospace and Electronic Systems,1985,21(1):70-78.
[15] Sheng X Q.A brief treatise on computational electromagnetics[M].2nd ed.Hefei:Press of University of Science and Technology of China,2008:17-42.(盛新庆.计算电磁学要论[M].2版.合肥:中国科学技术大学出版社,2008:17-42.)
[16] Gordon W.Far-field approximations to the Kirchoff-Helmholtz representations of scattered fields[J].IEEE Trans.on Antennas and Propagation,1975,23(4):590-592.
Characteristics analysis on forward scattering radar echoes
ZHAO Xiao-tong,GUO Kun-yi,SHENG Xin-qing,QU Quan-you
(Center for Electromagnetic Simulation,Beijing Institute of Technology,Beijing 100081,China)
Lots of applications are based on the bistatic radar system for its enhanced radar cross section (RCS)when the transmitter works on the forward scattering area (bistatic angle is larger than 135°).For radar in some practical situation,echoes include scattering signal and incident signal at a considerable range of the bistatic angle.The total field differs with the scattering field in many characteristics like phase,which will have influence on the applications of the forward scatter radar (FSR).The echoes of some FSR objects are simulated when the bistatic angle and distance between the receiver and the object changes.The echoes composition and characteristics are analyzed and the drawbacks of the shadow theory will be listed.
bistatic radar; forward scatter; echo characteristics; full-wave numerical method
2015-11-26;
2016-06-02;网络优先出版日期:2016-07-14。
国家自然科学基金-面上项目(61471041)资助课题
TP 18
ADOI:10.3969/j.issn.1001-506X.2016.11.12
赵晓彤(1992-),女,博士研究生,主要研究方向为雷达目标特性。
E-mail:694360944@qq.com
郭琨毅(1976-),女,硕士研究生导师,副研究员,博士,主要研究方向为雷达目标特性。
E-mail:guokunyi@bit.edu.cn
盛新庆(1968-),男,教授,博士研究生导师,博士,主要研究方向为电磁计算。
E-mail:xsheng@bit.edu.cn
屈泉酉(1988-),男,博士,主要研究方向为雷达目标特性。
E-mail:1426802347@qq.com
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20160714.1456.014.html

