基于卡尔丹方程的高分辨ROSAR成像算法及性能分析

张　俊,廖桂生,许京伟,朱圣棋

(西安电子科技大学雷达信号处理国家重点实验室,陕西 西安 710071)



基于卡尔丹方程的高分辨ROSAR成像算法及性能分析

张俊,廖桂生,许京伟,朱圣棋

(西安电子科技大学雷达信号处理国家重点实验室,陕西 西安 710071)

旋转式合成孔径雷达(rotor synthetic aperture radar,ROSAR)是一种新型的雷达成像模式,其圆形运动轨迹斜距历程造成传统二阶斜距近似法在宽方位波束场景下方位向散焦严重。针对这一问题,提出了一种基于卡尔丹方程解析表达式的ROSAR成像算法。考虑通过对回波信号的斜距表达式进行四阶近似,推导了回波信号的二维频谱,分析距离徙动对成像结果的影响,提出基于卡尔丹方程解析表达式实现距离徙动补偿,进而实现整个场景精确聚焦的成像算法并给出了算法的运算量。仿真实验验证了算法的有效性及在噪声环境下的稳健性。

旋转式合成孔径雷达; 二维频谱; 卡尔丹方程; 距离徙动; 四阶近似

0　引　言

合成孔径雷达(synthetic aperture radar,SAR)作为一种全天时、全天候的高分辨率成像雷达,在军事和民用领域有着广泛的应用[1-2]。旋转式合成孔径雷达(rotor synthetic aperture radar,ROSAR)是一种新型的雷达成像模式,它既保留了传统合成孔径雷达的优点,更具有重访周期短、全视域成像等优势,在应急救灾、自主避险等方面具有重要的应用价值[3-4]。

直升机ROSAR模式中,天线被固定在旋翼上,随旋翼一起做圆周运动,本质上,ROSAR成像是利用天线旋转运动形成的方位向圆弧实现合成孔径,从而在短周期内完成全视场二维成像。然而由于ROSAR天线运动轨迹为圆形,导致其斜距历程与传统直线SAR相比更为复杂,难以直接利用驻相原理计算二维频谱。文献[5]针对圆迹环扫SAR(CTSSAR)提出了二阶斜距近似求解驻相点的距离多普勒(range-Doppler,RD)算法,在方位角波束较小且距离分辨率较低的情况下,二阶近似可以满足成像的需求,但在方位角波束较大,距离分辨率要求较高的情况下,这种近似会产生较大误差,影响最终的成像结果。文献[6]提出的后向投影(back projection,BP)算法对于复杂频谱计算以及图像重建等问题都具有很好的效果,但由于对场景中的每一个点都进行了插值处理,整个算法的运算量巨大。文献[7]提出了一种改进ω-κ圆迹SAR算法,由于不需要计算驻相点,具有较好的聚焦结果,但计算量仍然较大。文献[8]提出了一种基于频域分析的ROSAR成像算法,其频谱展开仍然只保留二次项,虽然能够校正距离弯曲实现最终成像,但精度较低,当距离分辨率要求较高时,会由于距离徙动造成图像扭曲。文献[9]基于轨道近似的思想,将ROSAR的圆弧合成孔径转化为传统SAR的直线合成孔径,补偿相位误差后利用ω-κ算法进行聚焦,虽然能够实现最终成像,但图像散焦情况较为严重,难以满足高分辨的要求。

针对现有ROSAR成像算法存在的分辨率低、计算量大等问题,本文提出了一种新的高分辨ROSAR快速成像算法。通过分析推导ROSAR信号的斜距公式,对近似斜距的四阶项进行计算处理,基于卡尔丹方程解析表达式获得回波信号的二维频谱实现最终成像,分析了距离徙动对成像的影响并推导二维分辨率表达式,给出了整个算法的运算量分析,算法具有高分辨、低运算量的优点且在噪声环境下仍具有较好的稳健性。

1　ROSAR回波信号模型与问题分析

图1所示为ROSAR的几何模型。将天线固定在直升机旋翼上,其旋转半径为L,旋转角速度为ω。直升机载机高度为H,当天线旋转过一周时,会在地面形成一个圆环带照射场景。设天线俯仰角为φ,俯仰向波束宽度为θeBw,方位向波束宽度为θaBw,且天线照射方向始终与其运动方向垂直。为表述简便起见,选用圆柱坐标系表示目标方位,所以场景内的点目标P坐标为(rp,θp,0)。

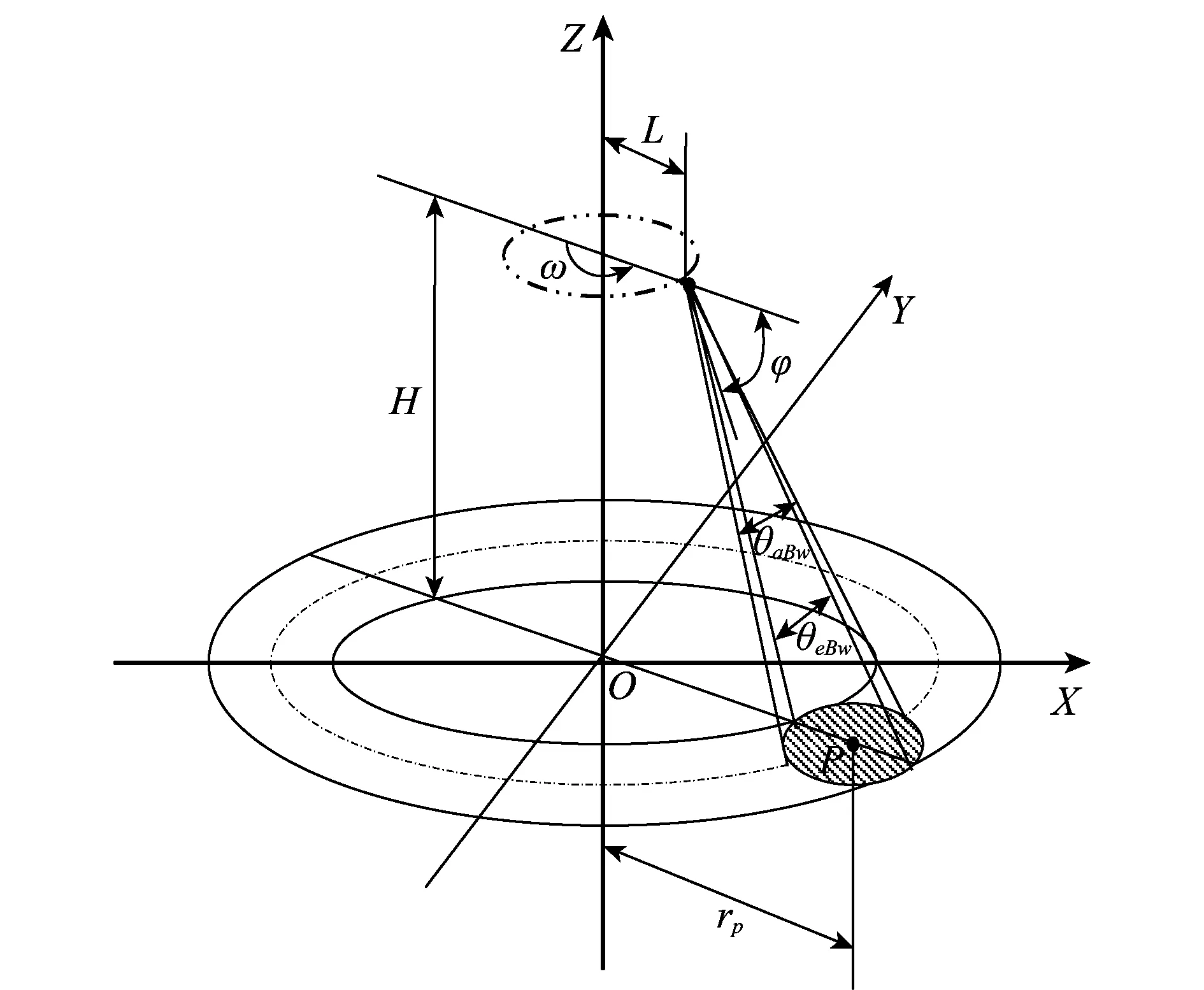
图1　ROSAR工作几何模型Fig.1　Geometric model of ROSAR

定义逆时针旋转方向为正,天线在某一时刻的旋转角为ωta,ta为慢时间,天线的位置可以表示为(L,ωta,H)。根据余弦定理,可以求出天线阵元与点目标P之间的斜距R(ta)表达式为

(1)

雷达发射的信号为线性调频信号,则点目标回波基带信号在距离-方位域(tr-ta域)形式可表示为

(2)

式中，Tp为发射脉冲宽度;γ为线性调频率;c表示光速;λ为雷达工作波长。下面结合式(1)推导回波信号sp(tr,ta)的二维频谱Sp(fr,fa)。

对式(2)沿距离向做傅里叶变换至距离频域,考虑到包络对成像结果影响很小,推导中忽略包络变化,因此得距离频率-方位信号表达式

(3)

式中，fr为距离频率;A1为距离向傅里叶变换后的信号包络。对式(3)沿方位向做傅里叶变换得到回波信号的二维频谱表达式

(4)

式中,fa为多普勒频率。已知距离频率二次项对方位向变换无影响,用驻相点法求解式(4)的积分变换形式,其积分项φ(ta)为

(5)

将斜距表达式(1)代入式(5),并关于ta求导。由驻相定理可知,满足积分项导数φ′(ta)取值为0时的ta为驻相点取值

(6)

2　基于卡尔丹方程的ROSAR成像方法

由上节中的分析可知,在推导ROSAR回波数据的二维频谱时,对其斜距近似的精确度将影响最终成像的质量。常用的二阶近似由于舍弃了高阶相位信息,在方位向波束宽度较大时会降低图像聚焦效果,由此考虑保留泰勒展开式中的四阶项,简化求解驻相点问题的同时,进一步提升了近似的精度,从而保证了最终成像的质量。

对式(1)中斜距R(ta)进行四阶泰勒级数展开如下

(7)

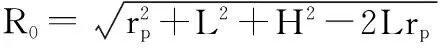
(8)

将式(8)代入式(5),得到近似后的相位φ(ta)为

(9)

(10)

利用式(10)求解驻相点

(11)

由上式不难看出,经过近似后的驻相点方程为三阶方程,既保留了更多的距离向信息,同时也对驻相点的求解进行了简化。求解相位φ(ta)的驻相点,实际是解式(11)的三阶方程的根。本文提出一种基于卡尔丹方程解析表达式的求解方法。将式(11)表达为卡尔丹方程标准形式,得到

(12)

其中l=0,且

(13)

(14)

根据卡尔丹方程性质[10]求解式(12),可知其存在判别式

(15)

式(15)取值不同时,卡尔丹方程的解对应不同的形式。

(1)当Δ≥0时,式(12)只存在一个实数解

(16)

(2)当Δ<0时,式(12)存在3个实数解

(17)

其中

(18)

在实际应用中,最终得到的是实数解,当Δ<0时,需要根据ROSAR的参数来选择,以确保实数解处于波束照射对应的一个脉冲周期之中从而具有实际的物理意义,即ta∈(-Tp,Tp)。

(19)

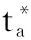
2.1相位误差分析

为了分析算法提出的四阶近似对成像结果的影响,需考虑高次项带来的相位误差。对斜距泰勒展开保留其高次项。由于展开后五次项系数为零,所以只考虑六次项带来的误差,更高次项的误差忽略不计,则有

(20)

其中q6为六次项系数,推导得出

(21)

由于实际应用中常存在fr≪fc,为简便起见,在计算相位误差时可将fr忽略不计。

选取ROSAR典型参数如表1所示,方位向波束θaBw的宽度选择90°,最终得到的六次项误差如图2所示。

表1　系统仿真参数

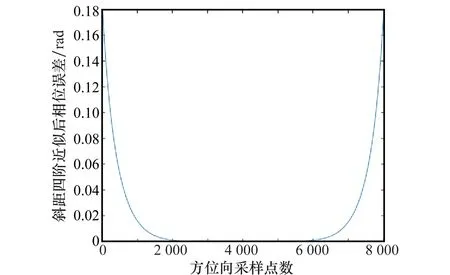
图2　四阶近似相位误差Fig.2　Phase error of fourth order polynomial

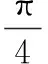
2.2距离徙动影响分析

在ROSAR模型下,对于距离半径相同,方位角不同的点目标,它们的距离徙动形状相同,表现为方位向的平移不变性。而对距离半径不同,方位角相同的点目标,它们的距离徙动形状也不相同,即表现为距离徙动空变性。这里主要讨论距离徙动的空变性,即相同方位角不同半径的点目标距离徙动。由式(1)定义距离徙动差为

(22)

式中,ΔR(θa,rsmax)表示场景最长边缘rsmax处的距离徙动;ΔR(θa,rsmin)表示场景最短边缘rsmin处的距离徙动;P(rsmax)与P(rsmin)分别表示场景最远处到天线的最短斜距与场景最近处到天线的最短斜距,即

(23)

由图1中ROSAR的几何模型易推出rsmax与rsmin的表达式

(24)

由式(24)可以看出,场景的最远距离rsmax与场景的最近距离rsmin均受俯仰角波束宽度θeBw的影响,俯仰角波束宽度不同时,最终得到的距离徙动差RCM(θa)也不同。选取俯仰角波束宽度θeBw为参变量,图3给出了距离徙动差RCM(θa)随方位角θa变化曲线图。

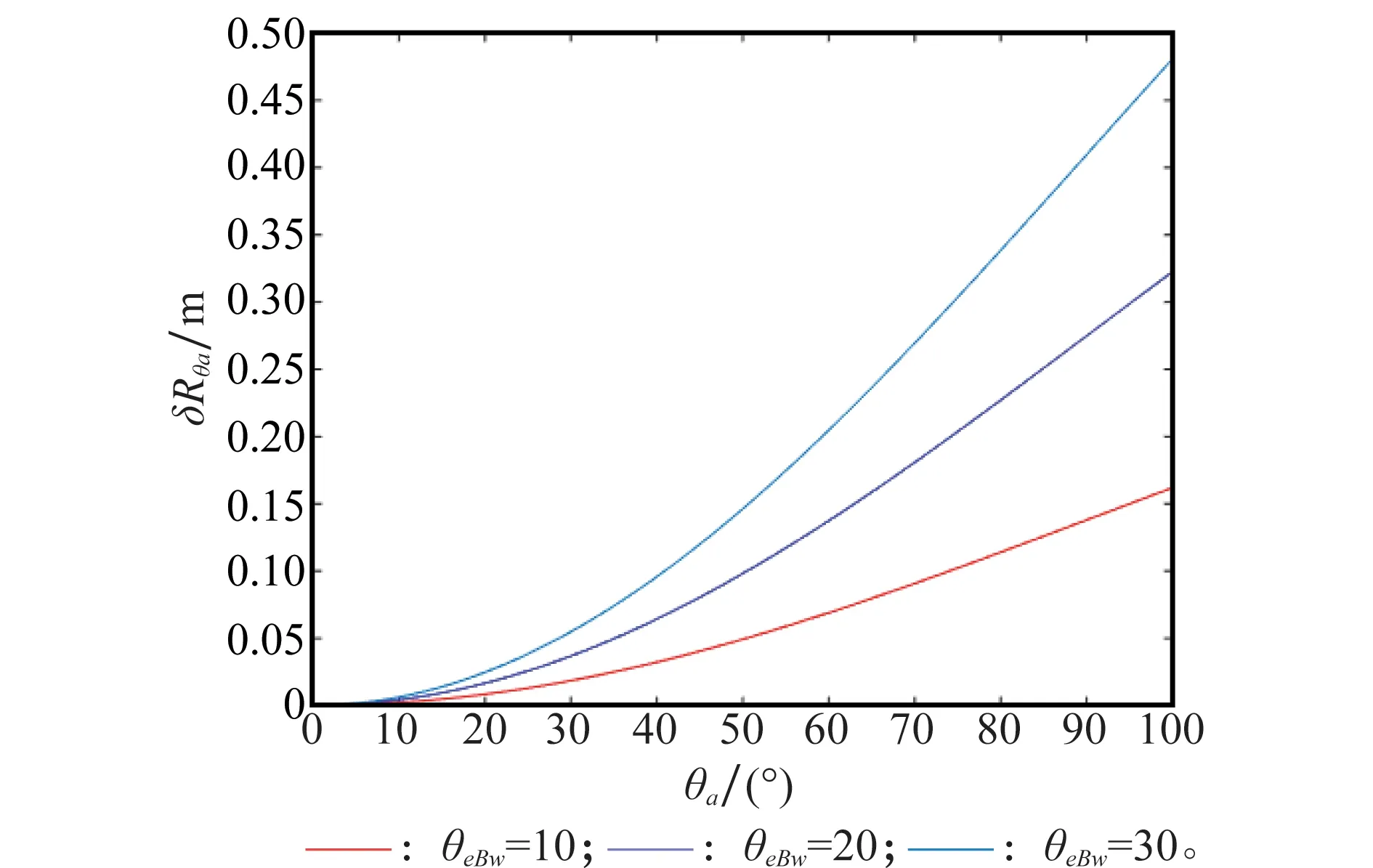
图3　距离徙动差RCM(θa)随方位角θa变化曲线Fig.3　Curve for rang cell migration difference Rcm(θa) respect to azimuthal angle θa

由图3可知,距离徙动差RCM(θa)随着方位角θa的增加而增加,且俯仰角波束宽度θeBw越大,距离徙动差的变化范围就越大。当距离分辨率ρr远大于距离徙动差RCM(θa)时,可以忽略距离徙动对最终成像的影响,但当距离分辨率ρr较高时,距离徙动差RCM(θa)的影响无法被忽略,需要考虑相应的补偿方法。

2.3具体成像流程

前几节分析推导了基于卡尔丹方程的ROSAR回波信号二维频谱及距离徙动对成像结果的影响。本节将讨论利用之前得到的二维频谱,并考虑高距离分辨条件下,通过消除距离徙动影响来设计算法成像流程。高距离分辨下,距离徙动对成像的影响不能忽略,若直接对此前推得的二维频谱进行方位压缩,只能对成像场景中心点附近精确聚焦,而场景边缘处的目标会由于距离徙动造成的多普勒调频率失配而导致散焦,因此,需要在方位压缩前对场景中产生距离徙动的目标进行补偿。考虑雷达系统参数满足如下关系

fc≫fr

(25)

所以可以将式(14)中的n近似为

(26)

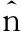
(27)

可以看出,近似后的相位也与距离频率无关,实现了距离向与方位向的去耦合,简化了补偿距离徙动相位差的操作。将式(27)代入式(19)得到新的二维频域表示式

(28)

选取与场景中心距离为Rc的一参考点,通过式(28)中距离为R0的点目标相位与距场景中心Rc的参考点相位相减得到需要补偿的距离徙动相位差

(29)

通过补偿式(29)所示的距离徙动相位差,就可以消除距离徙动带来的影响,实现方位向的良好聚焦。

整个算法的具体成像流程如下:

(1)通过二维快速傅里叶变换获得如式(19)所示回波信号的二维频谱;

(2)对信号进行距离脉压后,在频域对参考点处的频谱进行补偿,脉压函数与参考点补偿因子的表达式如下

(30)

(3)对补偿后的信号做距离向逆傅里叶变换至距离-多普勒域,对距离徙动相位差进行补偿,消除距离徙动对方位聚焦的影响,其补偿因子为

(31)

(4)进行方位向逆傅里叶变换得到最终聚焦的ROSAR图像。

图4给出了本文所提算法的流程图。

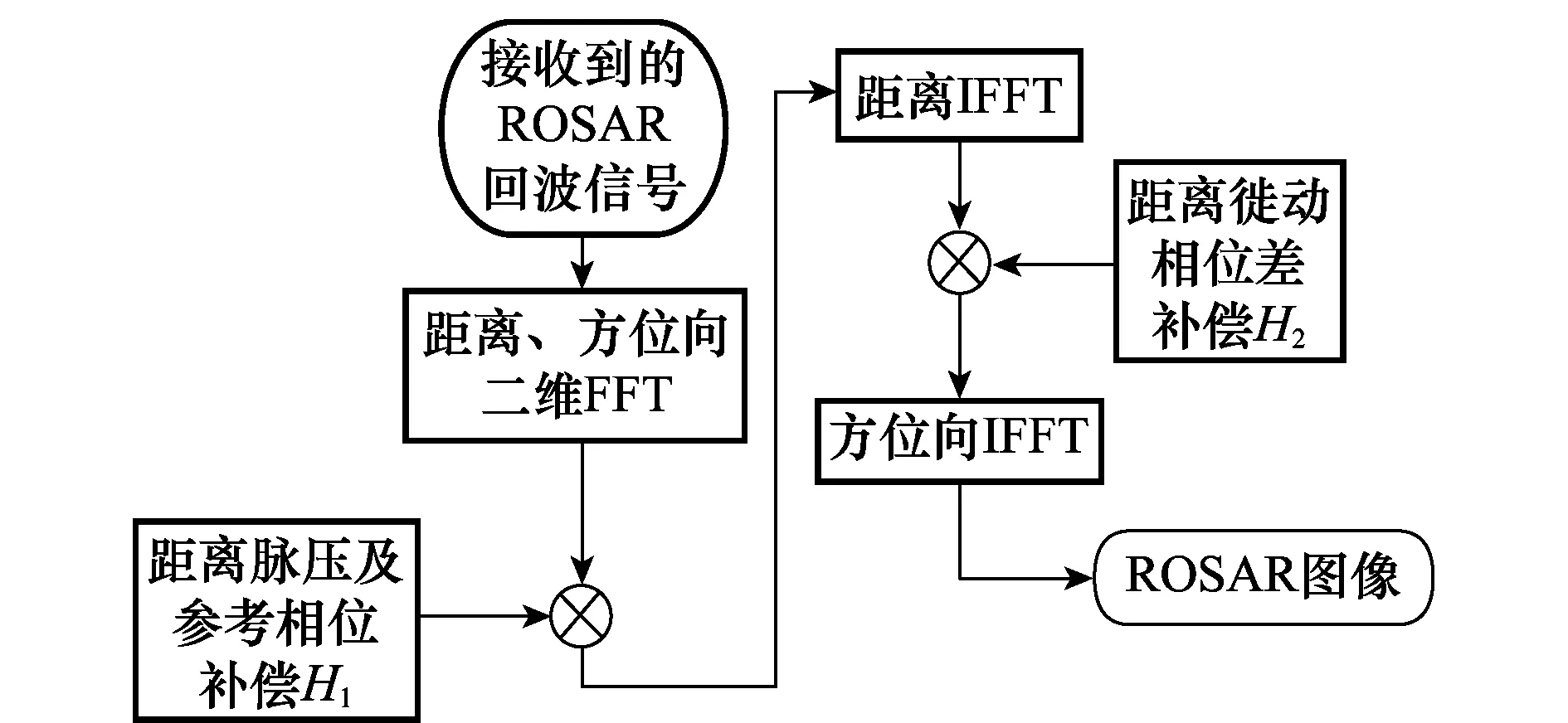
图4　算法流程图Fig.4　Flow diagram of proposed algorithm

2.4计算量分析

算法为获得更为丰富的相位信息实现良好聚焦,通过求解卡尔丹方程得到四次斜距历程的驻相点,在方位频域完成距离徙动的校正,避免了波数域算法距离徙动校正中的插值操作,有效降低了整个算法的运算量,本节通过估算浮点运算(floating point,FLOP)量,给出算法的计算量分析。

在成像算法中主要进行傅里叶变换/逆傅里叶变换、相位相乘、插值代换这三种基本操作,算法大部分的计算量都来自与这三种操作,因此分析中将不考虑匹配滤波器设置、预设插值核索引、插值点数等因素,而求解卡尔丹方程最终得到的是解析解,可以忽略其对算法计算量的影响。

已知N点FFT或IFFT的FLOT为5Nlog2(N),一次复数相位相乘需要6次,插值核长度为Nker时,每个通道内进行一次基带插值需要Nker次实数相乘与Nker-1次实数相加,由于复数据有两个通道,所以每一复输出点需要的所有FLOT为2(2Nker-1)。根据以上定义,结合图4的流程图,可以给出本算法的计算量

(32)

式中,Nra与Naz分别表示距离向采样点数与方位向采样点数,而插值核长度为Nker的插值操作的计算量为2(2Nker-1)NazNra/109,算法与传统ω-k等波数域成像算法相比,用距离徙动相位差补偿代替了插值操作,可以有效降低运算量。

图5给出了算法的计算量随回波采样点数变化曲线图,并与插值核长度为16的STOLT插值ω-k算法计算量进行比较,这里假定回波的方位向采样点数与距离向采样点数相同,不难看出当回波数据量较小时,两种算法的计算量接近,当数据较大时,本文所提算法计算量与ω-k算法相比明显降低。

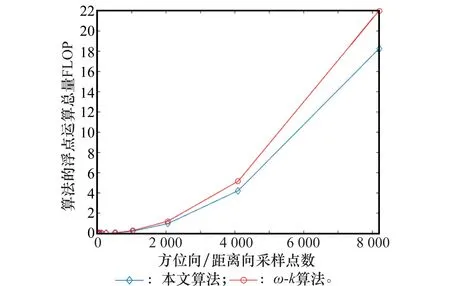
图5　计算量变化曲线Fig.5　Curve for variation of calculated amount

2.5分辨率性能分析

在距离维,ROSAR的距离分辨率与传统直线条带SAR相同,均为ρr=c/2B,其中B为信号带宽,c为光速。而在方位维,由于ROSAR方位维上方向随方位角的变化而改变,所以方位分辨率与传统直线条带SAR不同。假设有一点Q与点目标P位于同一平面且具有相同半径,而方位角差为Δθ,则可知其对应斜距为

(33)

对上式关于求导,得到对应的多普勒频差为

(34)

由于Δθ很小,所以上式又可以近似为

(35)

式中，PRF为脉冲重复频率；Na为方位向采样点数是距离点P最小方位分辨率的目标,则可推出对应的方位角分辨率为Δθ=λR0PRF/2NaωrpL。因此,方位分辨率为

(36)

式中，Td=N/PRF为方位积累时间；va=ωL为天线运动线速度。由于方位向采样点数与方位向波束宽度存在如下关系

(37)

表示取整操作,所以ROSAR方位向分辨率实际是关于方位向波束的函数

(38)

3　仿真实验结果

3.1算法与传统二阶近似成像算法对比实验

本节通过仿真实验,对比本文算法与传统二阶近似在不同方位向波束宽度条件下的最终成像结果,验证本文方法的有效性。为模拟载机平台低空工作场景,选取平台工作高度为500 m,考虑到实际直升机的旋翼长度,选取天线旋转半径为1.5 m,且天线的旋转速度与旋翼旋速相同,设置5个点目标,同一距离单元内的点目标方位向间隔为6°。ROSAR的系统参数如表1所示。

已知当方位向波束θaBw较窄时,采用二阶近似的方法也可以得到理想的成像结果,本文不再详细列举。当方位向波束θaBw为40°时,由图6可以看出,二阶斜距近似所得到的成像点在方位向上出现了旁瓣混叠,峰值旁瓣比(PSLR)下降,最终的成像质量下降;而本文所提方法在方位向仍能使主旁瓣较明显分开,峰值旁瓣比损失较少,聚焦效果良好。当方位向波束θaBw增大至70°时,可以看出二阶斜距近似的方位向混叠严重,主瓣展宽,严重散焦,难以满足成像要求;而四阶斜距近似在方位向也出现了部分旁瓣混叠,峰值旁瓣比损失接近1.61 dB,但仍能保持较好的函数形状,由之前相位误差分析可知符合成像要求,在成像质量要求不是特别高的情况下,可以采用本文的方法进行成像。

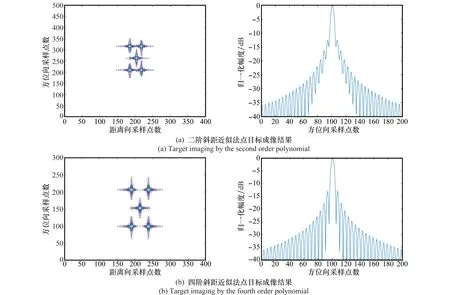
图6　θaBw=40°时两种方法成像结果Fig.6　Imaging by two methods when θaBw=40°

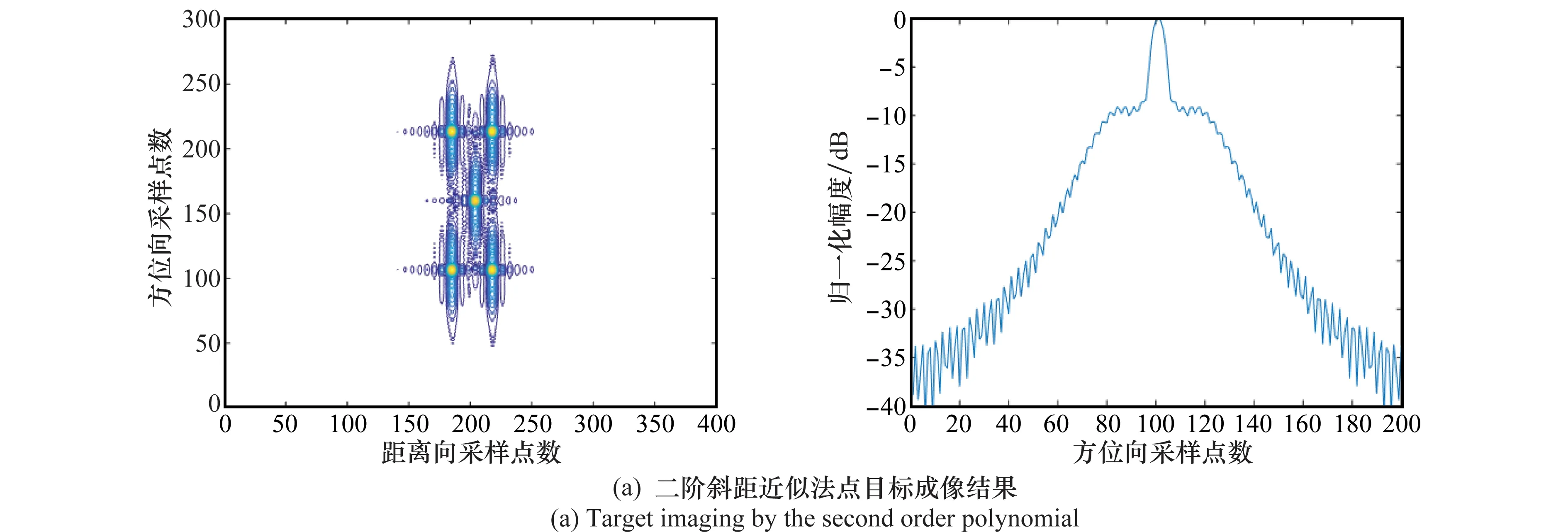
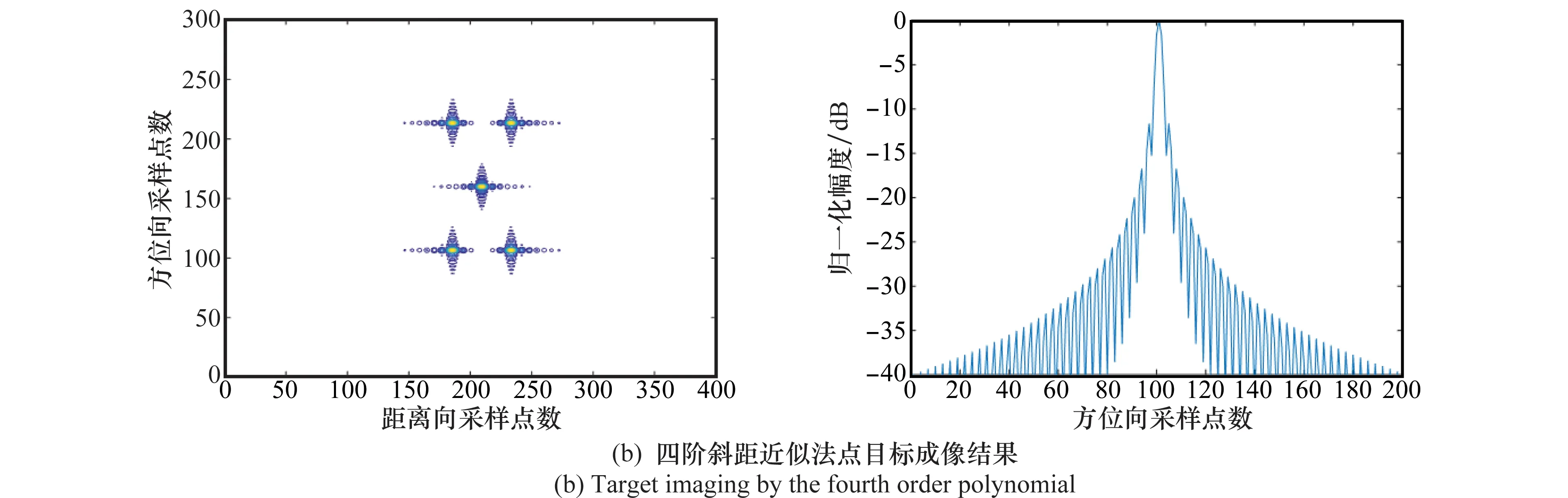
图7　θaBw=70°时两种方法成像结果Fig.7　Imaging by two methods when θaBw=70°

选取θaBw=40°时的中心点目标成像结果进行本算法的聚焦性能分析,给出积分旁瓣比(integrated side-lobe ratio,ISLR)的计算公式如下

(39)

式中，Ptotal、Pmain分别代表处理后的信号总功率与主瓣功率。在计算积分旁瓣比时,考虑到临近目标旁瓣会对中心点目标积分旁瓣比产生影响,所以选取200点方位向采样点数作为旁瓣宽度进行计算。由之前分析可知,ROSAR的距离分辨率理论值为0.45 m,方位向分辨率理论值为0.77 m。表2给出成像性能结果,可以看出,仿真点目标成像结果均与理论值接近,证明了本算法的可行性。

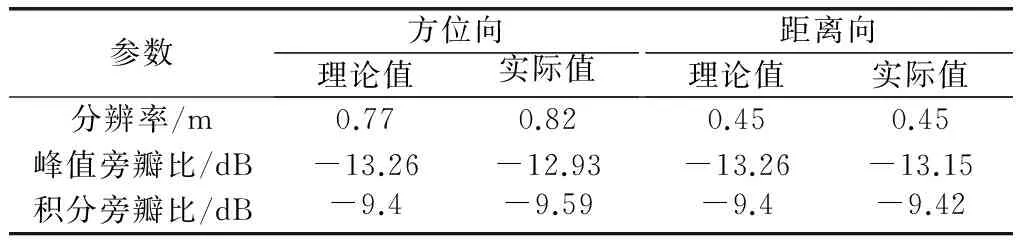
表2　算法成像点目标性能分析

3.2算法在噪声环境下的成像结果分析

本节通过在白噪声环境下对点目标成像结果分析,验证了本文算法的稳健性。ROSAR成像系统参数如表1所示,点目标设置与第3.1节相同,在背景高斯噪声功率为-10 dB的场景下,选取方位向波束宽度θaBw=40°为对点目标成像,最终成像结果如图8所示。

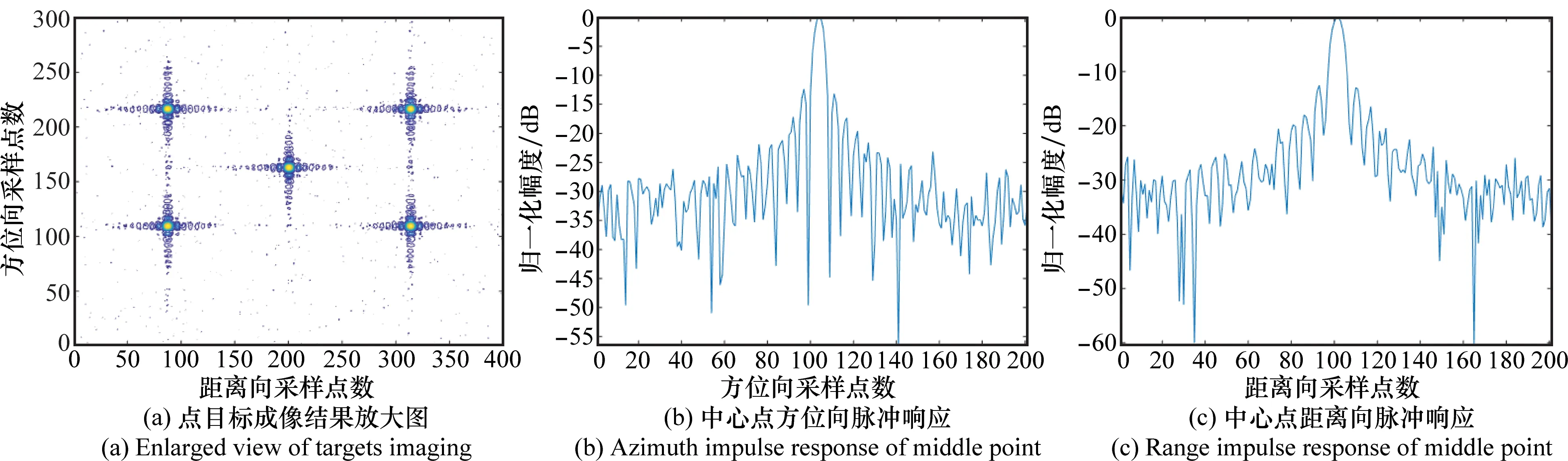
图8　噪声环境下点目标群成像结果Fig.8　Targets imaging in nosie

由图8可以看出,在-10 dB背景噪声环境下,最终的点目标成像结果仍能保持较好的聚焦结果与副瓣对称性。选取中心点进行性能分析,距离向与方位向的峰值旁瓣比分别为12.54 dB和12.37 dB,与第3.1节中无噪声场景中的成像结果对比,两维脉冲响应的峰值旁瓣比稍有衰减,但属于可接受范围之内。计算图像的最小熵值,复散射强度构成二维图像I,具体公式如下

(40)

式中，Na、Nr分别表示方位向采样点数与距离向采样点数；D(n,k)为图像的散射强度密度,通过式(40),可以计算出无噪声环境下聚焦后的图像最小熵值为6.47,噪声环境下聚焦后的图像最小熵值为8.73,相比于理想环境中的成像结果,图像熵值有所增大,但仍能保持良好的聚焦效果,证明了本算法在噪声环境下也能够实现精确成像,具有较好的稳健性。

4　结　论

本文提出了一种基于卡尔丹方程解析表达式的ROSAR成像新方法,推导旋转合成孔径下的斜距方程,对斜距进行了四阶近似处理后,求得驻相点解析表达式,从而获得回波信号的二维频谱,计算六次项相位误差,并分析距离徙动对最终成像的影响,设计了结合距离徙动补偿校正的成像算法,给出整个算法的计算量分析并与ω-k算法进行比较,证明算法具有低运算量的优点。仿真结果表明本文方法可以实现在宽波束覆盖情况下高分辨ROSAR成像,相比于传统方法成像质量明显提高,并且在噪声环境下成像仍能保持良好的聚焦效果,整个算法具有较好的稳健性。

[1] Skolnik M I.Introduction to radar system[M].New York:McGraw-Hill,2001.

[2] Brown W M.Synthetic aperture radar[J].IEEE Trans.on Aerospace and Electronic Systems,1967,3(2):217-229.

[3] Klausing H.Feasibility of a synthetic aperture radar with rotating antennas (ROSAR)[C]//Proc.of the 19th European Microwave Conference,1989:287-299.

[4] Nguyen B D,Migliaccio C,Pichot Ch,et al.W-band fresnel zone plate reflector for helicopter collision avoidance radar[J].IEEE Trans.on Antennas Propagation,2007,55(5):1452-1456.

[5] Sun B,Zhou Y Q,Chen J,et al.Operation mode of circular trace scanning SAR for wide observation[J].Journal of Electronics & Information Technology,2008,30(12):2805-2808.(孙兵,周荫清,陈杰,等.广域观测圆轨迹环扫SAR成像模式研究[J].电子与信息学报,2008,30(12):2805-2808.)

[6] Cantalloube H,Koeniquer E C.High resolution SAR imaging along circular trajectories[C]//Proc.of the IEEE International Geoscience and Remote Sensing Symposium,2007:850-853.

[7] Kou L L,Wang X Q,Chong J S,et al.Circular SAR processing using an improved omega-k type algorithm[J].Journal of System Engineering and Electronics,2010,21(4):572-579.

[8] Yang K,Liao G S,Xu Q,et al.ROSAR imaging algorithm based on frequency ananlysis[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(9):1189-1193.(杨科,廖桂生,徐青,等.基于频域分析的ROSAR成像算法[J].北京航空航天大学学报,2012,38(9):1189-1193.)

[9] Wang W,Liao G S,Li D,et al.A novel high-resolution imaging method for ROSAR[C]//Proc.of the IET International Radar Conference,2013:1-6.

[10] Eldhuset K.A new fourth-order processing algorithm for spaceborne SAR[J].IEEE Trans.on Aerospace and Electronic Systems,1998,34(3):824-825.

[11] Liao Y,Bao M,Xing M D,et al.High resolution imaging algorithm for circular trace scanning synthetic aperture radar[J].Systems Engineering and Electronics,2013,35(9):1847-1853.(廖轶,包敏,邢孟道,等.一种高分辨圆迹环扫合成孔径雷达成像方法[J].系统工程与电子技术,2013,35(9):1847-1853.)

[13] Ishimaru A,Chan T,Kuga Y.An imaging technique using confocal circular synthetic aperture radar[J].IEEE Trans.on Geoscience and Remote Sensing,1998,36(5):1524-1530.

[14] Migliaccio C,Nguyen B D,Pichot C.Millimeter-wave radar for rescue helicopters[C]//Proc.of the International Conference on Control,Automation,Robotics and Vision,2006:1-6.

[15] Goshi D S,Mai K,Liu Y,et al.A millimeter-wave sensor development system for small airborne platforms[C]//Proc.of the IEEE Radar Conference,2012:510-515.

[16] Li W C,Yang Y J,Huang Y L,et al.A geometry-based Doppler centroid estimator for bistatic forward-looking SAR[J].IEEE Geoscience and Remote Sensing Letters,2012,9(3):388-392.

[17] Li D,Liu H Q,Liao Y,et al.A novel helicopter-borne rotating SAR imaging model and algorithm based on inverse chirp-Z transform using frequency-modulated continuous wave[J].IEEE Geoscience and Remote Sensing Letters,2015,12(8):1625-1629.

[18] Kreitmair S W,Wolframm A P.HeliRadar-a rotating antenna synthetic aperture radar for helicopter all-weather operations[C]//Proc.of the 59th AGARD Guidance and Control Panel,1995:1-8.

[19] Shin H S,Lim J.T.Omega-k algorithm for airborne forward-looking bistatic spotlight SAR imaging[J].IEEE Geoscience and Remote Sensing Letters,2009,6(2):312-316.

[20] Sutor T,Buckreuss S,Krieger G.Sector imaging radar for enhanced vision (SIREV):theory and applications[C]//Proc.of the SPIE Enhanced and Synthetic Vision,2000:292-297.

[21] Krieger G,Mittermayer J,Wendler M,et al.SIREV-sector imaging radar for enhanced vision[C]//Proc.of the International Symposium on Image and Signal Processing and Analysis,2001:377-382.

High resolution imaging algorithm and performance analysis for ROSAR based on cardano’s formula

ZHANG Jun,LIAO Gui-sheng,XU Jing-wei,ZHU Sheng-qi

(National Lab of Radar Signal Processing,Xidian University,Xi’an 710071,China)

Rotor synthetic aperture radar (ROSAR)is a new kind of imaging mode,due to the complex expression of target’s range derived by its circular trajectory of motion,expanding target’s range to the second order brings severe defocussing in azimuth under the condition of wide-beam.To deal with this problem,a new imaging algorithm of ROSAR based on Cardano’s formula is proposed.Considering expanding the expression of target’s range to a fourth order polynomial and deriving the two-dimensional spectrum of echo,an effect of range cell migration (RCM)on image is made.The image is obtained by compensating RCM based on Cardano’s formula and the calculated amount of method is showed.Simulation results validate the feasibility and the robust in noisy environment of the proposed algorithm.

rotor synthetic aperture radar (ROSAR); two-dimensional spectrum; Cardano’s formula; range cell migration (RCM); fourth order polynomial

2015-12-24；

2016-04-17；网络优先出版日期：2016-07-14。

国家自然科学基金(61231017,91438106)资助课题

TN 957.52

ADOI:10.3969/j.issn.1001-506X.2016.11.10

张俊(1991-),男,博士研究生,主要研究方向为雷达成像与动目标检测。

E-mail:z395580835@163.com

廖桂生(1963-),男,教授,博士研究生导师,博士,主要研究方向为空时自适应信号处理、动目标检测、雷达成像与参数估计。

E-mail:gsliao@xidian.edu.cn

许京伟(1987-),男,博士后研究生,博士,主要研究方向为动目标检测、空时自适应信号处理。

E-mail:xujingwei1987@163.com

朱圣棋(1984-),男,副教授,博士研究生导师,博士,主要研究方向为空天平台目标检测与识别、雷达成像与动目标检测。

E-mail:zhushengqi8@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160714.1434.010.html