蒸发波导高度水平非均匀性对路径损耗的影响

庞佳玮 杜晓燕 张水莲 江长荫

（1.信息工程大学，河南 郑州450002；2.中国电波传播研究所，河南 新乡453003）

引 言

对流层无线电波导（简称对流层波导）主要源于在沿海拔高度方向上大气温度的逆变和湿度的剧烈变化而导致的大气折射率异常改变，它会严重影响电磁波的传播特性，这势必会影响为标准环境下设计的无线电系统的性能.目前，关于海上大气修正折射率结构的遥感探测方法主要是利用雷达回波反演折射率剖面的雷达回波反演大气波导（Refractivity From Clutter，RFC）方法.现有公开文献表明，采用该方法进行反演时应用的大都是文献［1］中对水平非均匀性的研究思路.

大量实验研究表明，对流层波导存在着显著的水平（沿电波传播方向）非均匀性，且其对电波传播特性及修正折射率的反演结果影响剧烈［2］.文献［1］结合实际数据仿真主要分析了5参数大气修正折射率剖面模型中逆变层逆差、逆变层基底高度（简称逆变层底高）的水平非均匀性对损耗分布的影响，得出模型中逆变层底高的水平非均匀性影响最大的结论，并由此提出11参数模型（垂直剖面模型用5个参数描述；水平方向只考虑5个参数中逆变层基底的水平非均匀性，用6个参数描述，认为其它4个参数沿电波传播方向不变，即忽略其水平非均匀性）.此外，文中还仿真得到增加逆变层底高的水平非均匀性描述可以改善反演结果.

此后的反演研究表明，不论是使用简单的蒸发波导模型还是相对复杂的混合波导模型，反演最优解对应的折射率剖面以及路径损耗分布通常不能与实际数据相匹配［3］.究其原因，除了由于海浪后向散射截面的随机性而造成的海杂波的不确定性之外，反演模型中对波导参数水平非均匀性描述不够充分也严重影响了反演的效果［3］.

依据文献［1］构建了由10个参数描述的具有水平非均匀性的混合波导模型.从正演的角度探讨了对流层波导模型中蒸发波导高度水平非均匀性对电波路径损耗的影响，得出某些条件下蒸发波导高度水平非均匀性不能忽略，并由此提出新的反演模型.从反演的角度，应用新模型，采用文献［4］中通信链路反演的方法，进行路径损耗空间分布的反演研究，得出新的反演模型可以有效提高反演计算的效果，由此验证了正演研究结论的有效性.

1 对流层波导参数模型

1.1 10参数大气修正折射率模型

10参数大气修正折射率模型从垂直和水平方向两个尺度上来描述修正折射率分布.垂直方向使用经典的5参数混合波导模型，水平方向取逆变层底高的非均匀性，运用马尔科夫过程来描述，并利用K-L变换实现模型的参数化［1］.

上述5参数混合波导模型也称为四折线模型，既包含蒸发波导模型，又包含表面波导三折线模型，以及介于二者间的混合层模型.该模型被广泛应用于对对流层波导的研究中，如图1所示.该模型的修正折射率垂直分布关系为

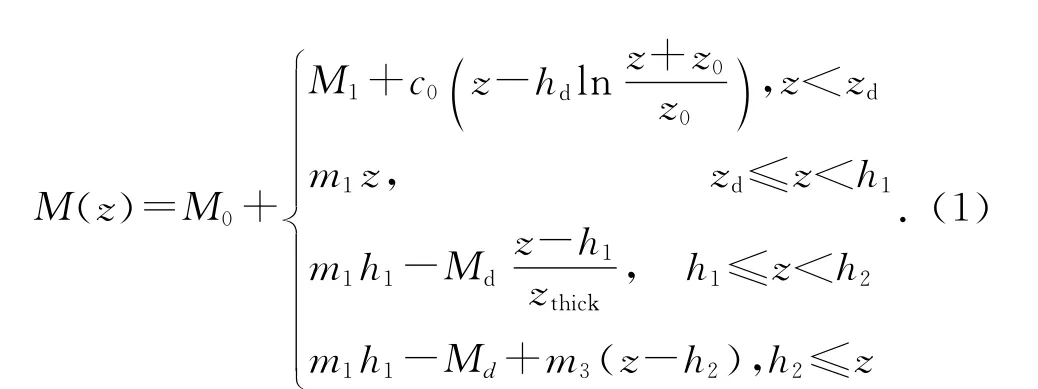
式中：z0是粗糙度因子（通常取0.000 15）；c0为中性层结蒸发波导参数（通常取0.13）；m3＝0.118 M-units/m；M0为混合层的延长线与z＝0相截的值（取为340）；M1＝（m1-c0）zd＋c0hdlogzd/z0；表征折射率垂直方向变化的5个主要参数如下：Md为逆变层逆差；zthick为表面波导的厚度；m1为混合层斜率；h1为逆变层底高；hd为蒸发波导高度.

图1 大气修正折射率5参数混合波导模型

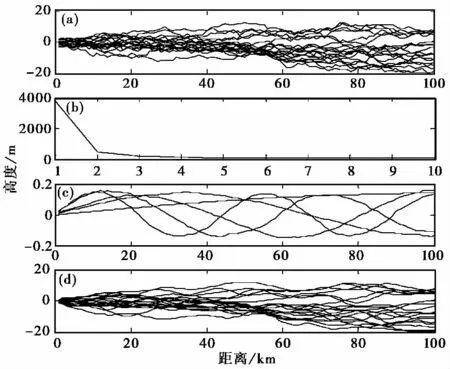
图2 波导逆变层底高随传播距离变化的模型

Gerstoft等人指出大气折射率的水平微小变化对电磁波的空间场强分布影响剧烈，并指出这种水平非均匀性可以用马尔科夫过程来描述［1］.图2（a）为模拟得到的马尔科夫过程20个样本，它显示出h1在100km尺度上变化的幅度.图2（b）为前10个特征值，图2（c）为5个主要的特征向量，不同于文献［1］的是只提取代表该过程主要特征的前5个特征量（只提取主成分中累计贡献率超过95%的前5个特征值）.图2（d）为基于5个主特征向量和相应特征值叠加组合的20个马尔科夫过程样本.利用该理论计算得到的h1在100km尺度上变化幅度控制在±20m内，且具有良好的随机性，与修正折射率在水平方向上的微小、随机的变化特点是相符的.5参数混合波导模型中的其余4个参数在水平方向上保持不变.

为讨论hd水平非均匀性的影响，构建了基于h1和hd水平非均匀性的新对流层波导模型，并进行正演仿真分析，以便研究，具体如下.

1.2 基于h1和hd水平非均匀性的新对流层波导模型

文献［1］认为，逆变层基底h1的水平非均匀性对路径损耗分布的影响占主要地位，所以文中采用的反演模型中忽略了其它4个参数的水平非均匀性.此后许多对流层波导的反演工作也是基于此结论展开的.为说明其他参数对电波传播正演的重要性，本节引入蒸发波导高度的水平非均匀性，参考产生h1的水平非均匀性的方法产生表征hd的水平非均匀变化的参数，并由此构建基于h1和hd水平非均匀特性的新对流层波导模型.

利用计算机模拟实现106个马尔科夫过程样本，每隔1km利用高斯随机数对hd更新一次，其变化幅度控制在±10m内，如图3（a）所示为其中的20个样本.

图3 蒸发波导高度随传播距离变化的模型

运用K-L变换的方法提取出马尔科夫过程的5个最主要的主特征向量eigenvectori（i＝1，2，3，4，5）和对应系数，并利用5个系数来表征折射率在水平方向的随机变化趋势.图3（b）为前10个特征值，图3（c）为5个主要的特征向量.图3（d）为基于5个主特征向量和相应特征值叠加组合的20个马尔科夫过程样本.对比图3（a）可以看出，利用5个主特征向量和对应特征值拟合所得曲线可以准确地描述图3（a）曲线的变化趋势.因而可以用5个水平参数coei（i＝1，2，3，4，5）.与5个特征向量重新拟合得到hd的马尔科夫过程.考虑到蒸发波导高度的变化范围相对较小，所以需要对生成的过程进行限幅.最后，hd在水平方向上的变化，可以表示为

此处5个水平参数的变化范围应小于对应特征值的方根，这样才能与大气折射率的微小变化相符［1］.至此，引入了h1和hd水平非均匀性，构建了新的15参数（h1和hd的水平非均匀性分别用5个参数描述，垂直方向特性仍用式（1）中的5个参数描述）大气修正折射率模型.

选取10个水平非均匀参数coei的组合，即可得到一组h1和hd的水平方向数据，图4即为由此得到的一个折射率二维分布图.

图4 由15参数波导模型构建出的一个大气修正折射率二维分布图

2 h1和hd的水平非均匀性的正演分析

本节基于15参数大气修正折射率模型，利用抛物方程法仿真计算，探讨h1和hd的水平非均匀性对电波路径损耗的影响.

2.1 抛物型方程法

通过地球展平变换和保角变化，结合尺度分析，可将Helmholtz方程简化为电磁波在大气中传播的抛物型方程（Parabolic Equation，PE）［5-7］：

式中：u为电场或磁场的函数（依赖于辐射场的极化方式；m为大气修正折射指数；x和z分别为电磁波传播的距离和高度.采用抛物型方程法，结合上述对流层波导垂直剖面模型即可计算路径损耗.

假设下边界z＝0是平滑的海面，由天线参数确定初始场，就可以利用分步傅里叶数值解法的抛物型方程法（FFT-PE）循环计算得到全空间的电波强度［7-8］.解的形式为

式中：k是真空中的波数；Δx是选择的步长；F（·）是傅里叶正弦变换；F-1（·）是傅里叶正弦逆变换.

众所周知，若忽略介质对电磁波吸收、散射等作用引起的损耗，实际中的电波传输损耗为

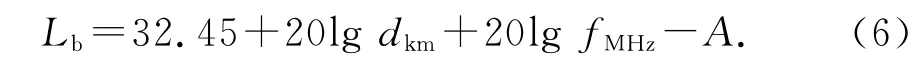
本文主要研究路径损耗.

2.2 仿真计算及分析

2.2.1 仿真模型

为方便讨论hd和h1的水平非均匀性对电波传输损耗的影响程度，构建出四个模型用于仿真：

模型一 （10参数模型）：考虑垂直高度上的5个参数和h1的水平非均匀性（用5个参数描述）；

模型二 （10参数模型）：考虑垂直高度上的5个参数和hd的水平非均匀性（用5个参数描述）；

模型三 （15参数模型）：考虑垂直高度上的5个参数，以及hd和h1的水平非均匀性（分别用5个参数描述），即1.2节中提出的模型.

模型四 （5参数模型）：只考虑垂直高度上的5个参数.

为仿真分析方便，上述四个模型中垂直方向上的5个参数分别取为：hd＝12，h1＝150，h2＝200，m1＝0.135，Md＝20.其水平非均匀性均采用1.2节中的方法生成，由此构建出上述四个模型以方便仿真计算.本节分别从hd和h1水平非均匀性及其初值设置（x＝0处的取值）两个方面开展仿真分析，以充分研究hd水平非均匀性对对流层波导条件下路径损耗的影响.

2.2.2 h1、hd水平非均匀性对电波路径损耗的影响

由发射天线参数和环境参数（如表1所示），利用1.2节中的方法各随机生成20组（即20种可能的水平非均匀分布）5参数随机组合，分别用于描述hd和h1水平非均匀性.由2.1节中的FFT-PE方法即可计算出模型一、二和三条件下电波路径损耗分布，以分别讨论hd和h1的水平非均匀性以及两个参数同时水平非均匀时对电波路径损耗分布的影响.

表1 发射天线和环境参数

图5、图6和图7分别为发射天线高度10m、50 m和170m时，仿真得到的70km、80km、90km和100km处路径损耗沿高度的分布，其中图（a）为利用模型一的仿真结果、图（b）为利用模型二的仿真结果、图（c）为利用模型三的仿真结果.

上述仿真结果表明，不同传播距离处，不同发射天线高度时，hd和h1的水平非均匀性对电波的路径损耗分布均有影响.这种影响与hd和h1的相对关系以及发射天线高度有关：

1）采用模型一仿真得到的结果中，h1的水平非均匀性对h1高度范围内路径损耗影响较大，而对相同情形下hd高度附近的路径损耗影响相对较小.天线发射高度为10m和50m时，此结论较显著.

图5 发射天线10m高度时利用模型一、二和三仿真得到的路径损耗在不同距离处沿高度的分布

图6 发射天线50m高度时利用模型一、二和三仿真得到的路径损耗在不同距离处沿高度的分布

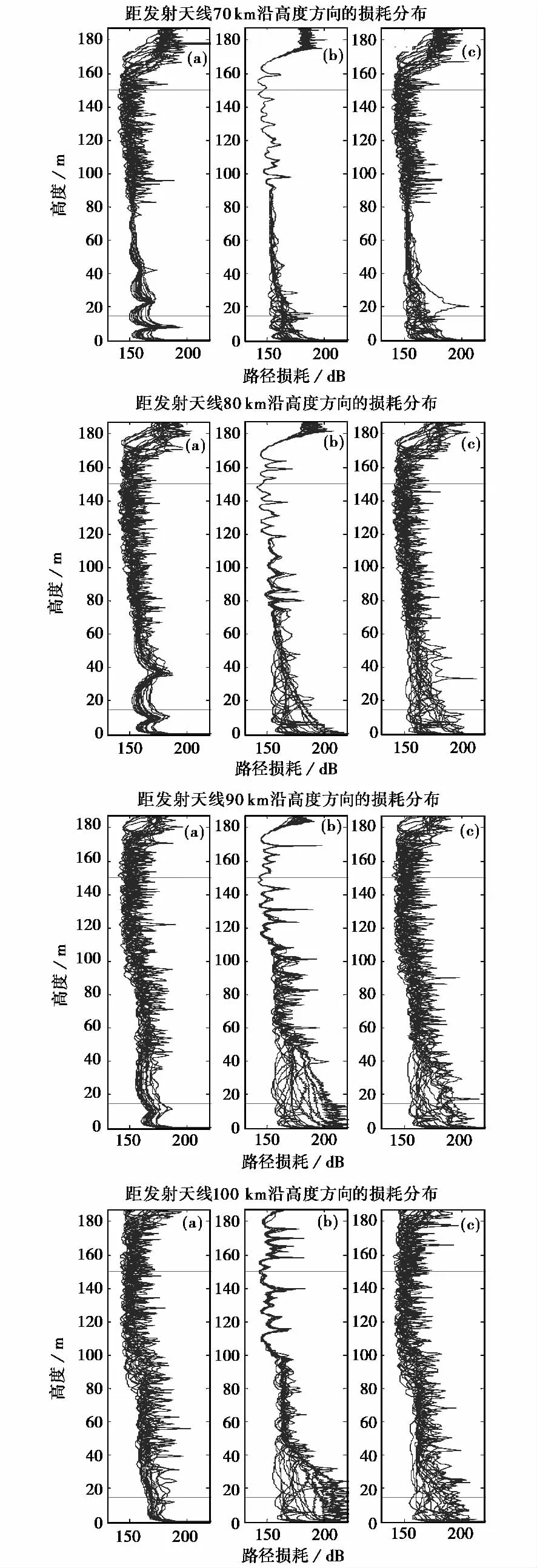
图7 发射天线170m高度时利用模型一、二和三仿真得到的路径损耗在不同距离处沿高度的分布

2）采用模型二仿真得到的结果中，hd的水平非均匀性对hd高度范围内路径传输损耗影响较大，而对相同情形下h1高度附近的路径损耗影响相对较小.天线发射高度为10m和50m时，此结论较显著.

3）采用模型三仿真得到的结果中，不论发射天线高低，hd和h1水平非均匀性对二者高度附近路径损耗的影响都较大.

2.2.3 h1和hd初值取值对电波路径损耗的影响

将模型三垂直方向5个参数中的hd和h1的初值（在传播距离为0处的取值）分别取下列组合：［15，120］，［15，180］，［12，150］，［18，150］（即hd和h1取值的改变均是在其初值［15，150］的基础上增加或减少初值的1/5），水平方向随机生成水平非均匀性.在此模型下，分别仿真计算发射天线高度10 m、50m和170m时，电波路径损耗的二维空间分布.图8、图9、图10和表2为垂直方向参数中hd和h1的四种不同取值组合情况下的计算结果，分别相对于初值［15，150］时计算结果的二维空间路径损耗分布的差值图，表2给出其二维空间平均相对差值.

表2 不同hd和h1取值组合下对应路径损耗的平均相对差值（%）

上述仿真结果表明：

1）当发射天线高度为10m和50m时，hd和h1在x＝0处的取值对电波二维空间路径损耗的影响相对较小，且几种情况下相差不大.

2）当发射天线高度为170m时，hd和h1在x＝0处的取值对电波二维空间路径损耗的影响相差较大.h1不同取值的影响较hd不同取值的影响大得多.由图10可以得出，hd的不同取值主要影响较低高度范围内（蒸发波导对应陷获层）的路径损耗分布.而h1的不同取值对整个二维空间中的路径损耗均有影响.

图8 10m发射天线高度时不同hd和h1的取值对正演影响

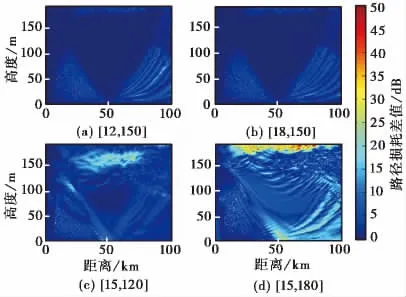
图10 170m发射天线高度时不同hd和h1的取值对正演影响

3 波导模型水平非均匀性对反演的影响分析

本节探讨本文中提出的15参数波导模型对反演效果的影响.为尽量避免海浪的随机散射截面带来的不确定性，本节利用文献［4］中的反演方法，基于通信链路，由收发天线间的路径损耗，通过不断改变大气修正折射率模型，应用优化算法对接收天线位置处路径损耗的计算值与目标值进行逼近，进而求得路径损耗的空间分布.

3.1 粒子群算法

由于波导参数与路径损耗间存在着复杂的非线性关系，这就要求反演算法必须能够克服局部极值影响，并适应复杂的非线性特性.粒子群优化（Particle Swarm Optimization，PSO）算法兼具全局和局部寻优能力，操作简单，收敛较快，已经成功地用于系统辨识、神经网络训练等领域.粒子在自身记忆、个体经验和社会经验的共同作用下，逐渐收敛于目标函数的全局最优位置.其位置和速度更新公式如下：

式中：ω为惯性权重，权衡算法局部最优与全局最优的能力；r1和r2为［0，1］之间的随机数，用来保持群体多样性；c1和c2为学习因子，表示粒子自我总结和向群体中优秀个体学习的能力［8］.pbest和gbest分别指个体经历的最优值，和群体经历的最优值.

实际应用中合理设置惯性权重、最大速度、种群数和搜索次数，可以得到较好的反演效果.由此，建立关于接收位置路径损耗计算值Lbr与其目标值Lbo的适应度函数：

式中，x为波导参数组成的向量，分别是修正折射率剖面垂直方向的5个参数和水平方向的5个参数.

3.2 反演仿真及分析

3.2.1 目标值生成及反演参数设置

本节采用2.2.1节中的模型三，正演得到三个不同高度发射天线（天线参数和环境参数同表1）条件下的路径损耗的空间分布（如图11所示），并在其中分别选取90km处最小路径损耗作为反演计算的目标值，目标值及其对应高度如表3所示.

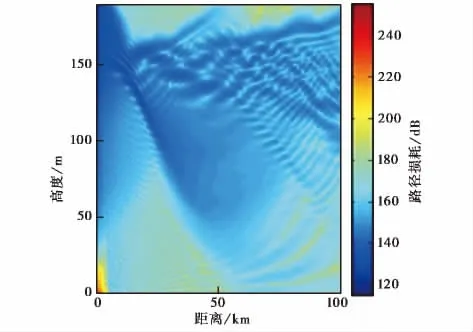
图11 170m发射天线下正演得到的路径损耗空间分布

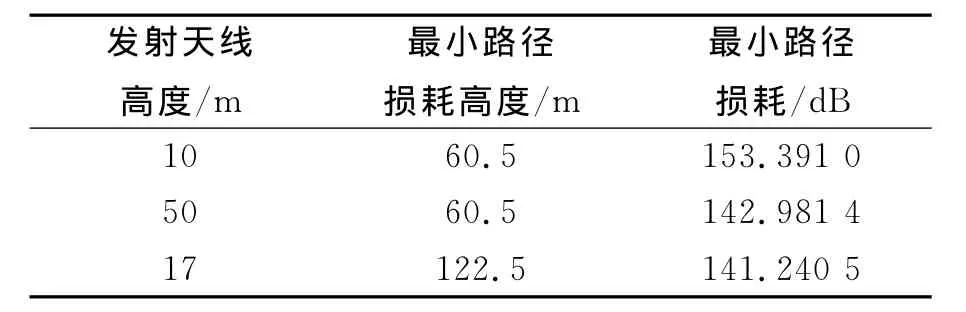
表3 三个不同高度发射天线90km处最小路径损耗（反演目标值）

本文分别采用粒子群算法参数为：种群数量20，迭代次数20，学习因子均为1.5，最大速度0.5/6，惯性权重0.4～1.2.参数搜索范围：垂直方向5参数中高度的搜索范围为20，斜率的搜索范围为0～1，波导厚度搜索范围为20.水平非均匀10参数的搜索范围小于各自对应特征值的方根.运用2.2.1中的四个模型进行不同高度发射天线条件下的反演计算，每种情况重复反演仿真20次，利用反演所得模型参数的平均结果再次利用抛物方程法计算空间中各位置的路径损耗.

3.2.2 反演结果及分析

将所得路径损耗空间分布仿真结果均减去3.2.1中其相应的正演结果，如图12、图13和图14所示.其中子图分别采用2.1.1节中的模型一、模型二、模型三和模型四.

图12 发射天线高度10m时，应用不同模型反演所得二维损耗相对正演结果的误差分布

表4 发射天线高度10m时不同模型反演所得路径损耗在不同传播距离处平均相对误差（%）

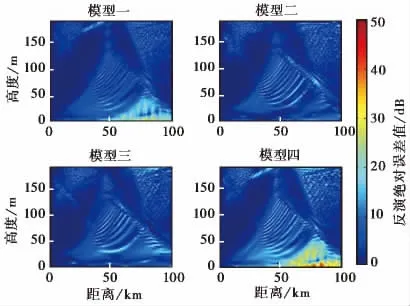
图13 发射天线高度50m时，应用不同模型反演所得二维损耗相对正演结果的误差分布

图14 发射天线高度170m时，应用不同模型反演所得二维损耗相对正演结果的误差分布

表5 发射天线高度50m时不同模型反演所得路径损耗在不同传播距离处平均相对误差（%）

表6 发射天线高度170m时不同模型反演所得路径损耗在不同传播距离处平均相对误差（%）

上述仿真分析结果表明：

1）发射天线为10m时，模型二所得反演结果较模型一的略差，但明显好于另两种模型所得反演结果.

2）当发射天线为50m时，模型三所得反演结果较模型二的略差，但明显好于另两种模型所得反演结果.

3）当发射天线高度为170m时，反演结果中，由模型三所得反演结果最好，而模型一和二所得结果较差，甚至不如5参数波导模型（模型四）.说明：发射天线较高时，需要综合考虑hd和h1水平非均匀性.单独引入hd和h1的水平非均匀性会导致反演效果的恶化，其原因还待更进一步探讨.

4 结 论

本文研究了对流层波导模型中蒸发波导高度的水平非均匀性对电波传输损耗的影响，得出发射天线高度较低时hd的水平非均匀性不能忽略，并由此提出新的对流层波导反演模型：当研究区域位于蒸发波导层内时，主要考虑hd的水平非均匀性，即采用模型二；当研究区域较高时（如在混合层中，甚至更高时），主要考虑h1的水平非均匀性，即采用模型一.由此，可以在反演模型参数增加不多的情况下，得出更具适应性的反演模型.文中应用新的反演模型，采用通信链路反演的方法，对路径损耗空间分布进行反演，验证了新的反演模型可以有效提高反演计算的效果.

通过研究还发现反演过程中并不是反演模型参数越多反演效果越好.当发射天线高度较高时，h1和hd的水平非均匀性的引入反而会使反演效果恶化，其原因还有待进一步探讨.此外，尽管本文仅就具体的对流层波导模型参数开展正演和反演研究，但所研究模型中包含了目前使用的所有波导模型，且在研究过程中，发射天线在波导各层中均有分布，因此，所得结论可以推广到更一般的对流层波导条件下的研究.

［1］GERSTOFT P，ROGERS L T，KROLIK J K.Inversion for refractivity parameters from radar sea clutter［J］.Radio Sci，2003，38（2）：1-22.

［2］YARDIM C，GERSTOFT P，WILLIAM S H.Sensitivity analysis and performance estimation of refractivity from clutter techniques［J］.Radio Sci，2009，44（1）：1-16.

［3］VASUDEVAN S，ANDERSON R H，KRAUT S，et al.Recursive Bayesian electromagnetic refractivity estimation from radar sea clutter［J］.Radio Sci，2007，42（2）：1-19.

［4］庞佳玮，杜晓燕，张水莲，等.粒子群优化算法反演无线电波导传输损耗分布［J］.电波科学学报，2013，28（1）：14-20.PANG Jiawei，DU Xiaoyan，ZHANG Shuilian，et al.Inversing the distribution of radio duct transmission loss？？using PSO algorithm［J］.Chinese Journal of Radio Science，2013，28（1）：14-20.（in Chinese）

［5］BARRIOS A E.Parabolic equation modeling in horizontally inhomogeneous environments［J］.IEEE Trans Antennas Propag，1992，40（7）：791-797.

［6］BARRIOS A E.A terrain parabolic equation model for propagation in the troposphere［J］.IEEE Trans Antennas Propag，1994，42：90-98.

［7］AKBARPOUR R，WEBSTER A R.Ray-tracing and parabolic equation methods in the modeling of a tropospheric microwave link［J］.IEEE Trans Antennas Propag，2005，53（11）：3785-3791.

［8］TRELEA I C.The particle swarm optimization algorithm convergence analysis and parameter selection［J］.Information Processing Letters，2003，85：317-325.