非平稳海杂波的消除趋势波动分析

丁 昊 关 键 黄 勇 于仕财 何 友

（海军航空工程学院信息融合技术研究所，山东 烟台264001）

引 言

对海雷达面临的海杂波背景随雷达分辨率的提高往往表现出复杂特性（如：非高斯性［1-3］、非平稳性［4-5］和非线性［6-9］等），这些特性因雷达参数、环境参数和地理位置的不同而有所差异.海杂波特性分析的重要意义在于它可以为海杂波建模、目标检测等问题提供必要的先验信息.根据研究问题的需要，海杂波特性分析的研究内容主要包括海杂波后向散射系数、统计特性和非线性特性等.非线性特性由于能够反映出海杂波更为本质的动态属性，目前已经成为国内外的热点研究内容［7-9］.

分形属于非线性特性研究领域的典型内容，通常采用波动分析（FA）方法进行研究，FA刻画了序列的二阶统计特性［8］.当序列存在非平稳性时，FA往往无法反映出真实的标度特性.消除趋势波动分析（DFA）是 Peng等人［10］在研究脱氧核糖核酸（DNA）序列时提出的一种标度分析方法，是研究非平稳、长程幂率相关性时间序列的重要工具［10-12］.与FA相比，DFA更加适合于非平稳信号的分形标度特性分析.DFA在海杂波特性分析及目标检测领域已经取得了初步研究成果.文献［9］从目标检测的角度出发，采用DFA研究了实测海杂波在三种数据域（幅度、幅度的部分和以及幅度的一阶差分）的分形标度特性，结果表明前两种数据域的特性差异可以区分海杂波与目标，然而并没有研究标度指数在不同尺度范围内的差异.文献［13］认识到了标度特性中出现的交叉标度现象及其对目标检测的不利影响，通过选取最优尺度区间，设计出一种基于联合分形特性的目标检测算法，并对检测性能进行了分析，存在的问题在于对DFA分析结果缺乏进一步解释.为此，本文结合DFA基本原理，对海杂波的分形标度特性进行了深入研究，主要研究内容包括：不同尺度范围内海杂波与目标单元的标度指数特性分析、交叉标度的出现原因、海洋环境参数对分析结果的影响以及分析结果对目标检测算法设计的指导意义.通过研究得出了有价值的结论，为深入理解海杂波的分形标度特性及目标检测算法设计提供参考和依据.

1 实测数据描述

采用两种不同体制、不同波段的实测海杂波数据进行分析.＃1数据的测量平台为加拿大 Mc-Master大学的X波段智能像素处理（IPIX）雷达，每组数据都包含4种极化方式和14个距离单元.数据采集期间雷达的脉冲重复频率为1 000Hz，距离向采样率为10MHz.为了验证分析结果是否通用，采用自行研发的雷达中/视频数据采集器在某海域采集得到的海杂波数据（＃2）进行对比分析.试验雷达为C波段岸基对海雷达，架设于固定平台上，数据采集期间雷达工作在驻留模式，距离向采样率为20 MHz.

在图1中，分别给出了两类采集数据的时域图形，其中，＃1数据采集期间的最大浪高为0.94m，有效浪高为0.63m，海况等级较低.从图1（a）可以看出：HH、VV极化的＃1数据时域特征差异十分明显，HH极化数据更加尖锐，而VV极化数据的相对幅度较高.＃2数据的时间-距离二维平面图如图1（b）（123页）所示，所有距离单元均不含目标，在某些距离单元上，海杂波具有很强的功率水平.

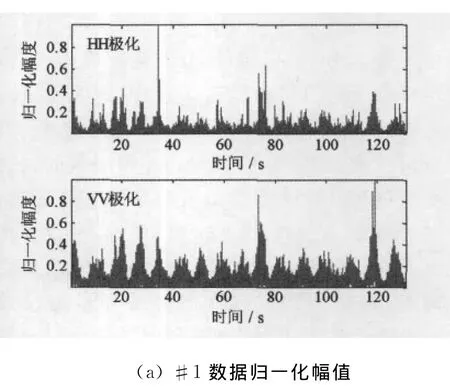
图1 实测数据的时域图形

2 非平稳性和分形的判定

海表面时变的粗糙结构导致海杂波具有复杂特性，而非平稳性和非线性特性中的分形特性正是其复杂特性的具体表现.非平稳性一般根据分段数据均值/方差的差异［14］或者信号的谱图进行判定.分形特性所研究的系统建立在自相似的基础上.对于理想的分形过程，在任何标度（即广义上的尺度）下，系统局部与整体的不规则性都具有自相似性.实际系统仅在一定的区间内满足自相似性，即无标度区间，因此，通过判定是否存在无标度区间就可以实现分形的判定.

2.1 非平稳性判定

首先采用分段数据的均值/方差判定非平稳性.任意选取某一距离单元的海杂波幅度为研究对象，将数据分成等长数据段，每个数据段包含1 024个采样点，相邻数据段之间重叠50%，然后估计出每段数据的均值和方差.以HH极化的＃1数据和＃2数据为例，计算结果分别如图2（a）、（b）所示.

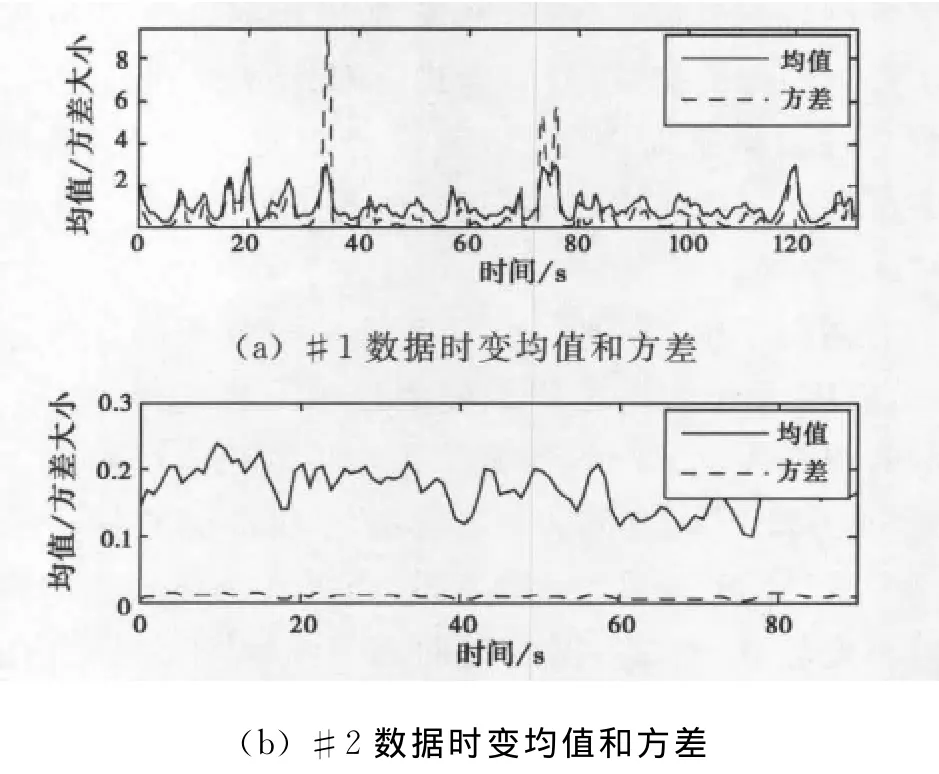
图2 海杂波的非平稳性判定

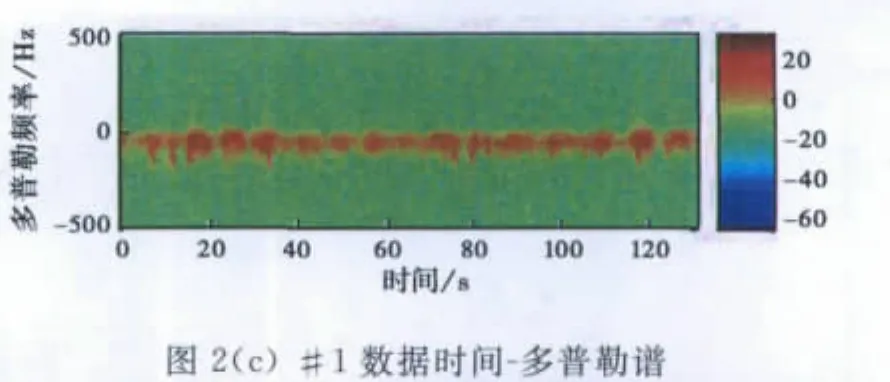
由图2（a）和（b）可知：随着时间的推移，均值和方差均具有一定的周期性起伏趋势，表明海杂波具有非平稳性.进一步采用谱图对非平稳性进行判定，数据分段方式同上，采用Hanning窗加权的快速傅里叶变换（FFT）算法计算每段数据的多普勒谱，结果分别如图2（c）、（d）（见123页）所示.可以看出多普勒谱存在一定程度的扩展，且大部分能量集中在低频附近，谱图中的周期性趋势主要是由长波对Bragg波的调制引起［15］.谱图的时变特性同样证实了海杂波的非平稳性.

2.2 分形判定

采用随机游走模型中所提的方法判断海杂波的分形特性［9］.设X表示均值为μ的平稳随机序列，从序列中减去μ得到序列x＝｛xi，i＝1，2，…，N｝，则“随机游走”过程y（n）定义为

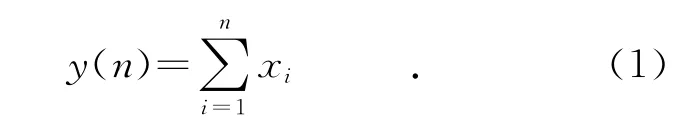
实际上，xi即为y（n）的增量过程 .对于y（n），若存在如下幂率关系：

则认为y（n）为一个分形过程，m为时间间隔（即尺度）；H为Hurst指数.为了便于分析，将式（2）的两端同时取对数，即

在特定的尺度范围内，如果海杂波幅度满足式（3）中的线性特性，则认为海杂波具有分形特性，与之对应的尺度范围称为无标度区间.

从＃1和＃2数据中选取连续的14个距离单元，其log2F（m）～log2m 曲线分别如图3（a）、（b）所示.可以看出：在尺度24～212和22～211范围内曲线近似呈线性，即在该时间段内海杂波具有标度不变性.根据判定方法，可以认为本组海杂波具有分形特性.通过直线拟合可知：＃1数据海杂波单元的Hurst指数在0.086～0.121的范围内变化，＃2数据的变化范围为0.013～0.019.Hurst指数起伏范围都很小，表明无标度区间内相邻距离单元海杂波具有相对稳定的分形特性.

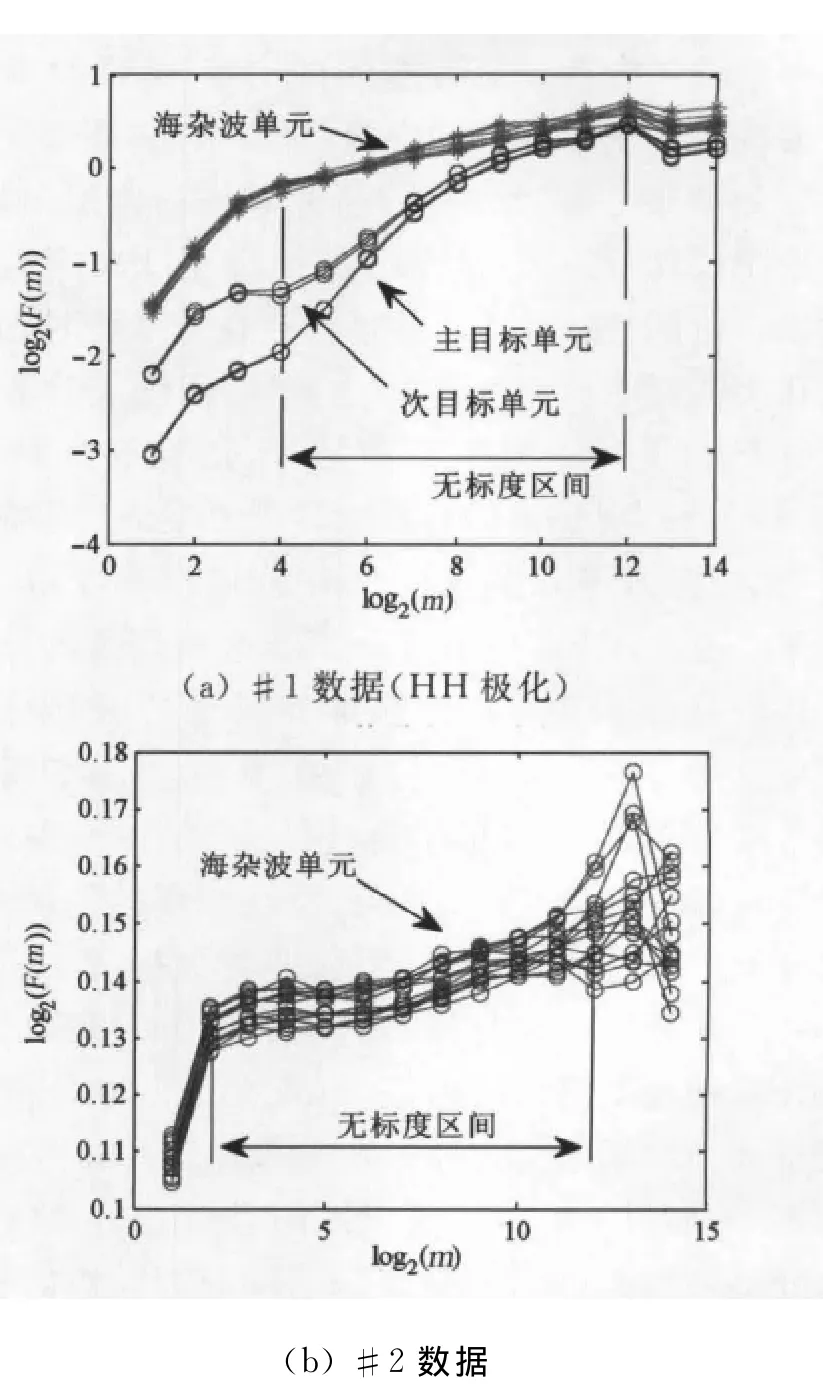
图3 海杂波的分形判定

3 长程相关性和DFA基本原理

3.1 长程相关性

具有分形特性的信号模型有很多，最为常用的是分数布朗运动模型.该模型在海杂波建模与目标检测算法等方面已经得到了广泛的应用，并表现出优异的性能，其主要特性包括自相似性、长程相关性、功率谱满足指数规律等.长程相关性是分数布朗运动模型的重要性质之一，它从统计意义上反映了海杂波未来变化趋势与当前变化趋势间的依赖关系，并通过一个归一化参数（即相关指数）对这种依赖关系的强弱进行度量.

海杂波的长程相关性可以通过对数方差-尺度法进行定性检验，该方法利用了序列的二阶自相似过程［7］.由其基本原理可知，当对数方差-尺度曲线的斜率大于-1时，就认为待检验序列具有长程相关性.对于上文中给出的两组海杂波数据，检验结果分别如图4（a）、（b）所示，曲线的斜率明显大于-1，表明海杂波幅度具有长程相关性.

图4 海杂波幅度的对数方差曲线

在定量分析海杂波的长程相关性时，由于序列中存在非平稳性和未知趋势，因此直接计算相关指数会引起较大的偏差，特别是时间延迟较大时，相关指数的值始终在零附近波动，因此无法直接得到幂率关系中的相关指数.这一问题可以采用消除趋势波动分析（DFA）方法解决.

3.2 DFA基本原理

DFA建立在随机游走理论的基础上，对于海杂波幅度序列X＝｛Xi，i＝1，2，…，N｝，DFA 主要包含4个步骤［11-12］：

第1步，计算幅度序列的累积离差Y（j），即

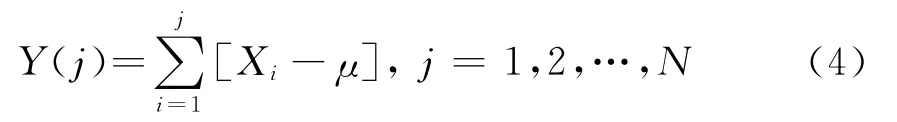
式中μ表示均值.

第2步，将Y（j）分割成Ns个互不交叠的等长区间，每个区间的长度（即尺度）为s.由于序列总长度并不总是区间长度的整数倍，因此序列末端的一小段数据无法有效参与运算.为了充分利用有效数据，对序列的逆序列进行同样的分组操作.

第3步，当尺度为s时，对于每个数据区间v（v＝1，2，…，2 Ns），分别采用最小二乘拟合算法计算局部趋势项wnv，并从累积离差中减去wnv得到残差，然后计算残差数据的方差F（v，s），其中，对于区间v＝1，2，…，Ns，有

对于区间v＝Ns＋1，…，2 Ns，有

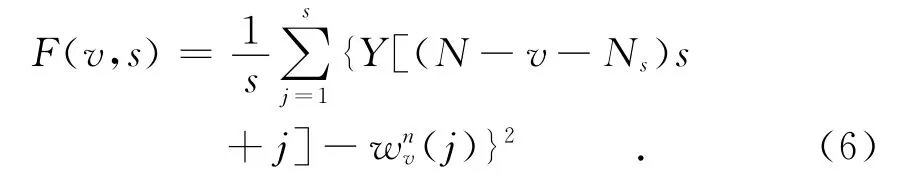
根据局部趋势项拟合阶数的不同，可以将DFA细分为DFA1、DFA2、DFA3以及DFAm，对应的拟合多项式分别为线性、二阶、三阶以及m阶多项式.不同阶数的DFA对趋势项的滤除能力不同，其中，DFAm可以滤除累积离差序列中的m阶趋势项，或者原始序列中的m-1阶趋势项.

第4步，在所有的数据区间上对方差取均值并做开方运算，得到DFA波动函数F（s），即

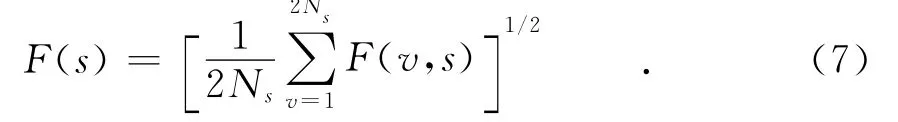
改变尺度s，并重复第2步至第4步的运算.如果序列具有长程幂率相关性，那么波动函数与尺度s之间满足幂率关系

式中α称为标度指数，它类似于波动分析中Hurst指数的概念，是DFA方法中度量时间序列相关性的重要指标.当0.5＜α＜1时，与相关指数γ之间存在如下关系

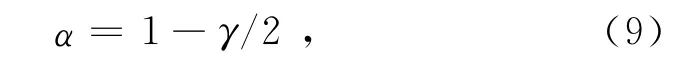
当α＝0.5时，序列不相关或者仅具有短期相关性；当α＞0.5时，序列具有持续性的长程相关性，即未来变化趋势很可能与当前变化趋势一致，且α值越接近于1，趋势增强的程度也越大；当α＜0.5时，序列具有反持续性的长程相关性，即未来变化趋势很可能与当前变化趋势相反，反持续性的程度随α的减小而增强.

4 实测数据分析

分析过程中尺度范围的选取是需要重点考虑的问题.尺度过小时，由于每段数据包含的样本数较少，对标度指数的估计会产生较大的偏差；尺度过大（与N接近）时，由于分割的区间数较少，波动函数的统计特性不稳定.本文中，尺度s的取值范围为

4.1 ＃1数据分析

采用＃1数据在HH和VV极化模式下的幅度数据进行分析.在所有的14个距离单元上，采用一阶DFA得到的log2F（s）～log2（s）曲线分别如图5（a）、（b）所示，从图中可以得到以下结果.

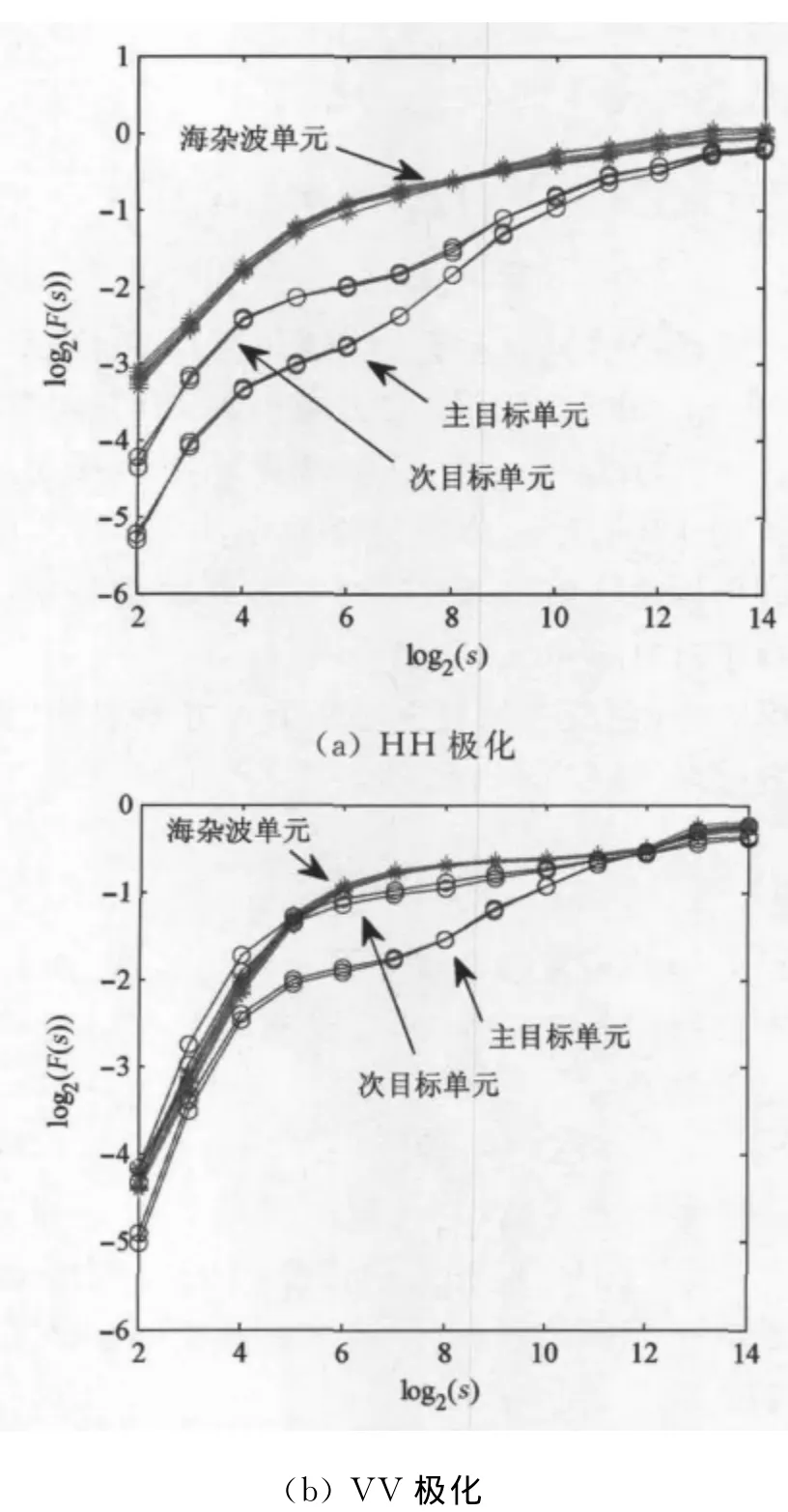
图5 ＃1数据的一阶DFA分析结果

1）对于海杂波单元，相同尺度上各距离单元波动函数的变化较小，与图3（a）相比可知，DFA能够提取出更加稳定的分形特性.log2F（s）～log2（s）曲线并没有呈现出单一的线性增大趋势，两种极化条件下均存在交叉标度，交叉点所在的尺度均为26左右，对应时间约为64ms，交叉点两侧的标度指数存在差异，且VV极化时的差异更加显著.

为了定量分析标度指数的差异，在表1中给出了不同尺度范围内标度指数的统计参数，包括均值、方差、最大值和最小值.可以看出：当尺度范围为22～26时，两种极化方式下标度指数的均值及最大/最小值都大于0.5，表明海杂波具有持续性的长程幂率相关性；VV极化时的标度指数更大，表明其变化趋势的持续性程度更强.通过对海杂波的短期时间相关性分析可知［1］，VV极化海杂波的相关时间较长，因此小尺度下的相关性也更强，这与本文分析结果相一致.当尺度范围为27～214时，标度指数的均值、最大/最小值都远小于0.5，表明海杂波具有反持续性的长程幂率相关性 .两种尺度范围内标度指数的方差都很小，表明DFA是一种稳健的特性分析方法.

2）在目标单元，波动函数呈现出更加复杂的变化趋势，从总体上可以将log2F（s）～log2（s）曲线分解为具有三个不同标度指数的线性区间.当尺度为22～24时，标度指数较大；当尺度为25～27时，log2F（s）线性增加的速度较为缓慢，标度指数较小；当尺度为28～214时，标度指数又发生了变化，最终波动函数稳定在一个值附近.以主目标单元为例，HH极化数据在三个区间的标度指数分别为0.983、0.309、0.264，而 VV 极化时分别为1.245、0.130、0.217.可见，目标单元仅在22～24的尺度区间内具有持续性的长程相关性，与海杂波单元相比其持续时间更短.出现这种差异的本质原因是目标的出现改变了海表面的分形结构，因此其特性异于海杂波单元.

3）无论是海杂波单元还是目标单元，随着尺度的增加，波动函数都会收敛到同一个值附近，此时，海杂波与目标特性已经相似，进一步增加尺度进行分析已经失去意义.

交叉标度通常是由不同尺度下相关性的改变或者数据中存在的固有趋势引起，下文中将对交叉标度出现的原因进行初步分析.

由DFA基本原理可知［12］：如果海杂波中存在p阶单调趋势，那么当DFA阶数m大于趋势阶数p时，log2F（s）～log2（s）曲线中不存在由趋势项引起的交叉标度.根据此原理可以分析海杂波中交叉标度的出现原因，具体方法为：增加DFA阶数并分析交叉标度所在尺度的变化情况，如果交叉标度向大尺度方向移动，且在DFA阶数增加到一定程度时，交叉标度消失，则其是由海杂波的趋势项引起，否则是由不同尺度下海杂波的相关性改变引起.需要注意的是，为了兼顾波动函数的计算精度，DFA阶数的选取不能过大.

表1 不同尺度范围的标度指数统计特性

以VV极化的＃1数据为例，海杂波和主目标单元在DFA1～DFA4情况下的log2F（s）～log2（s）曲线如图6所示.选择VV极化数据是因为交叉标度两侧的标度指数差异更加显著，有利于分析交叉标度的变化趋势.由图可知：在海杂波单元上，当DFA阶数增加时，交叉标度并没有消失，也没有向大尺度方向移动的趋势，表明交叉标度是由海杂波自身的相关性在不同尺度下的差异引起.

海杂波单元上波动函数对DFA阶数的敏感程度与尺度有关，以29为临界尺度，小于该值时，波动函数对DFA阶数较为敏感，在相同的尺度下，DFA阶数越高，波动函数的值越小，这主要与高阶DFA对海杂波局部趋势的拟合更加精确有关.当尺度大于29时，各阶DFA波动函数在相同尺度上基本相同，表明大尺度范围内由阶数变化引起的拟合精度差异基本可以忽略不计，波动函数主要受海杂波本身的长程相关性影响，对DFA阶数变化并没有敏感性.在目标单元，交叉标度也没有随着DFA阶数的增加而变化，同时，在所有的尺度上，高阶DFA具有更小的波动函数，这与海杂波单元的特性并不相同.

4.2 ＃2数据分析

采用＃2数据得到的分析结果分别如图7（a）、（b）、（c）所示，其中，图7（a）反映了相邻14个距离单元一阶DFA的log2F（s）～log2（s）曲线，它与图3（b）中的曲线相对应；图7（b）为同一距离单元上DFA1～DFA4的log2F（s）～log2（s）曲线；图7（c）为不同尺度范围内标度指数随DFA阶数的变化关系.

通过图7（a）与图3（b）比较可知，log2F（s）～log2s曲线在相邻海杂波距离单元具有更加稳定的特性，表明采用DFA分析非平稳海杂波的分形标度特性要优于传统的波动分析方法.图7（b）与图6对应，分析结果同＃1数据一致，其中临界标度为28.图7（c）是图7（b）中不同尺度范围内标度指数的直观结果，可见，小尺度范围内，随着DFA阶数的增加，标度指数接近于线性增加，而大尺度范围内，标度指数基本是恒定的，与DFA阶数无关.

图7 ＃2数据的DFA分析结果

4.3 海洋环境参数的影响

当海洋环境参数改变时，海杂波特性通常也会随之变化.为了进一步验证分析结果是否具有通用性和普适性，选择IPIX雷达在海况较高条件下采集的＃3数据进行分析，数据采集期间的最大浪高为3.02m，有效浪高约为2.01m.经验证，该组数据同时具有非平稳性和分形特性，HH、VV极化数据的一阶DFA分析结果分别如图8（a）、（b）所示，通过与图5的对比可知，交叉标度现象仍然存在，对应的尺度约为26，且VV极化的标度指数在交叉标度两侧的差异更加显著.

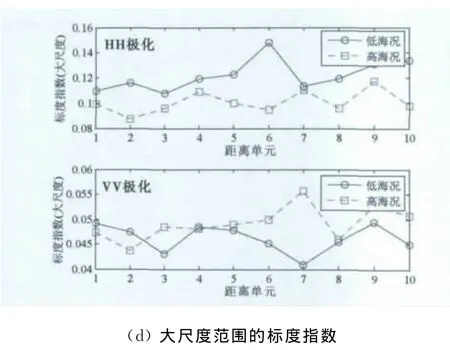
图8 海洋环境参数的影响分析

为了定量分析海洋环境参数对标度指数的影响，在图8（c）、（d）中，分别给出了不同尺度范围内（分别为22～26和27～212）海杂波单元的标度指数在各距离单元间的分布情况.可以看出：在小尺度范围内，HH极化时低海况的标度指数均高于高海况，VV极化时除个别距离单元在高海况时标度指数较大外，其余距离单元与HH极化时的结论相同；在大尺度范围内，HH极化条件下标度指数随海况的变化规律与小尺度时相同，而VV极化时高海况的标度指数从总体上看要高于低海况.这就表明：海洋环境参数对海杂波分形标度特性具有重要影响，且影响程度与极化方式密切相关.

4.4 分析结果对检测算法的指导意义

海杂波特性分析的主要目的之一在于提取出海杂波单元与目标单元间的特性差异并以此构成检验统计量实现目标的有效检测.通过上述分析不难发现，在目标单元，log2F（s）～log2（s）曲线的起伏规律明显异于海杂波单元，为此，曲线中的诸多特征量均可用于构成目标检测算法中的检验统计量.本节以拟合误差为例，对分析结果在目标检测算法中的应用进行验证性分析.在大尺度范围内，主目标单元log2F（s）～log2（s）曲线的直线拟合精度明显低于海杂波单元，为此，以拟合误差作为检验统计量，并设定合适的阈值，如果拟合误差与周围距离单元相比发生变化并高于检测阈值，则认为目标存在.

为了验证检测性能，以＃1HH极化数据为例，分别从海杂波单元与主目标单元取1 000段数据，每段数据包含10 000个采样点，数据段之间存在一定的交叠，依据DFA分析结果计算各段数据的拟合误差，结果如图9所示.可以看出，除了少部分数据段存在混叠外，其余数据段中海杂波与目标基本上都可以区分开，选择其余组数据也可以得到类似的结果，这就证明了检测算法的有效性.

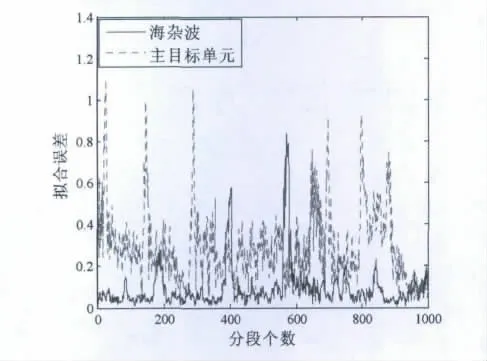
图9 不同数据段的拟合误差

5 结 论

通过本文的研究，得出的主要结论如下：

1）在非平稳条件下，采用DFA方法得到的海杂波log2F（s）～log2（s）曲线具有更加稳定的特性，优于传统的波动分析方法.

2）海杂波的相关性在不同尺度下的差异导致log2F（s）～log2（s）曲线中存在交叉标度，其中小尺度范围的标度指数较大，且与DFA阶数有关，大尺度范围的标度指数较小，对DFA阶数的变化并没有敏感性.VV极化时交叉点两侧标度指数的差异更加显著.

3）海洋环境参数变化时，以上结论仍然成立；同时，海洋环境参数对海杂波分形标度特性具有重要影响，且影响程度与极化方式密切相关.

4）由于目标单元与海杂波单元的log2F（s）～log2（s）曲线在起伏特性上存在诸多差异，因此分析结果可以为目标检测算法设计提供依据.

下一步将开展更多有针对性的数据采集试验，对海杂波特性进行更为深入的研究，并揭示其深层次的物理机理.同时，还要将研究结果与目标检测算法相结合，进一步提高海杂波背景下的目标检测性能.

图1 （b）＃2数据时域二维平面图

［1］CONTE E，MAIO A D，GALDI C.Statistical analysis of real clutter at different range resolutions［J］.IEEE Transactions on Aerospace and Electronic Systems，2004，40（3）：903-918.

［2］ANASTASSOPOULOS V，LAMPROPOULOS G A，DROSOPOULOS A.High resolution radar clutter statistics［J］.IEEE Transactions on Aerospace and Electronic Systems，1999，35（1）：43-60.

［3］扈罗全，林乐科，朱洪波.三种重拖尾分布海杂波的比较与分析［J］.电波科学学报，2007，22（6）：1061-1067.HU Luoquan，LIN Leke，ZHU Hongbo.Comparison and analysis of three kinds of distribution of sea clutter with heavy tails［J］.Chinese Journal of Radio Science，2007，22（6）：1061-1067.（in Chinese）

［4］DINESH R，JEFFREY K.Adaptive radar detection in doubly nonstationary autoregressive doppler spread clutter［J］.IEEE Transactions on Aerospace and Electronic Systems，2009，45（2）：484-497.

［5］HAYKIN S，DAVID J T.Signal detection in a nonstationary environment reformulated as an adaptive pattern classification problem ［J］.Proceedings of the IEEE，1998，86（11）：2325-2344.

［6］HAYKIN S，REMBRANDT B，BRIAN W C.Uncovering nonlinear dynamics-the case study of sea clutter［J］.Proceedings of the IEEE，2002，90（5）：860-881.

［7］关 键，刘宁波，张 建，等.海杂波的多重分形关联特性与微弱目标检测［J］.电子与信息学报，2010，32（1）：54-61.GUAN Jian，LIU Ningbo，ZHANG Jian，et al.Multifractal correlation characteristic of real sea clutter and low-observable targets detection［J］.Journal of Electronics ＆Information Technology，2010，32（1）：54-61.（in Chinese）

［8］盛 文，任 吉.高频雷达海杂波的多重分形建模方法研究［J］.电波科学学报，2011，26（5）：983-989.SHENG Wen，REN Ji.Multifractal modeling method for HF radar sea clutter［J］.Chinese Journal of Radio Science，2011，26（5）：983-989.（in Chinese）

［9］HU J，GAO J B，POSNER F L，et al.Target detection within sea clutter：A comparative study by fractal scaling analyses［J］.Fractals，2006，14（3）：187-204.

［10］PENG C K，BULDYREV S V，GOLDBERGER A L，et al.Statistical properties of DNA sequences［J］.Physica A，1995：180-192.

［11］KANTELHARDT J W，KOSCIELNY-BUNDE E，REGO H A，et al.Detecting long range correlations with detrended fluctuation analysis［J］.Physica A，2001：441-454.

［12］BASHAN A，BARTSCH R，KANTELHARDT J W，et al.Comparison of detrending methods for fluctuation analysis［J］.Physica A，2008：5080-5090.

［13］XU X K.Low observable targets detection by joint fractal properties of sea clutter an experimental study of IPIX OHGR datasets［J］.IEEE Transactions on Antennas and Propagation，2010，58（4）：1425-1429.

［14］饶 彬，屈龙海，肖顺平，等.基于时间序列分析的弹道目标进动周期提取［J］.电波科学学报，2011，26（2）：291-296.RAO Bin，QU Longhai，XIAO Shunping，et al.Precession period extraction of ballistic targets based on time series analysis［J］.Chinese Journal of Radio Science，2011，26（2）：291-296.（in Chinese）

［15］GRECO M，BORDONI F，GINI F.X-band sea-clutter nonstationarity：influence of long waves［J］.IEEE Journal of Ocean Engineering，2004，29（2）：269-283.