圆形口径平面天线阵列的多约束稀布优化方法
唐 斌 陈客松 杨晓波
(1.电子科技大学电子工程学院,四川 成都610054;2.成都航空职业技术学院航空电子工程系,四川 成都610100)
引 言
圆口径天线阵能在360°范围形成任意方向的波束,所以在诸如舰船、飞机等运动载体上和地面雷达系统中都具有重要的应用[1-2].当阵列口径较大时,半径间隔半波长的均匀同心圆环平面阵需要相当多的阵元,这使得天线系统的成本较高[3].为保证高的空间分辨率,低的副瓣特性等性能,同时又尽量降低天线系统的成本,可采用稀布天线阵元位置的方法来设计圆口径天线阵列,以提高性价比.
优化设计稀布天线阵列是复杂的非线性优化过程[4],一种方案是对均匀间隔阵列进行稀疏化设计,可获得稀疏阵列[5];另一种方案是阵元随机稀布,约束相邻阵元间距不小于半波长,以减小阵元间的互耦和消除栅瓣,后一种方案可使阵元在优化布阵过程中有更大的自由度,因而可获得比稀疏阵列更优的性能[6-7],文献[8-10]中称它为稀布阵列 .近年来,随着计算机技术的飞速发展,研究高效的稀布阵列的设计方法正逐渐受到重视[9-16].对圆口径天线阵列,国内外研究者已经展开了稀疏化的设计方法研究[10-12,16],但对更复杂的稀布优化设计的方法研究还未见报道,本文研究约束口径、阵元数和最小阵元间距的圆口径阵列的稀布优化设计方法.
由于非均匀圆形阵的归一化方向图的数学表达式无法用像线阵一样的解析式来表示,要导出波束宽度、旁瓣电平等与阵元数、阵半径的关系是非常困难的,只能用数学仿真的方法来论证试验[2].对于多约束的“稀布”圆口径平面阵综合问题,至今国内外还没有文献报道过基于遗传算法的实现,这是因为遗传算法应用于多约束最优化问题时会遇到诸如怎样找到可行解,如何避免不可行解在遗传操作后的子代中出现,以及计算量大等不少实际的困难[10],本文将它作为研究主题来讨论.
1 稀布圆口径阵列多约束综合
遗传算法是一种全局性概率搜索算法,其基本思想是模拟生物进化过程,目前已经应用于大量复杂的最优化问题中.由于遗传算法的普遍适用性,它在阵列天线设计等电磁学问题中正广泛地应用着[10-12],它可以求解非线性优化,所以适合于求解圆口径阵列的稀布优化问题.
1.1 优化问题的描述
不妨设优化布阵问题为如图1所示的半径为R的圆口径平面阵,平面xoy上,阵元位置用极坐标表示为dn=rnejφn,阵元数为 N+1(N 为正整数,1表示口径心处始终布置一个阵元),所有阵元相同且均匀等幅激励,为保持口径圆约束为R,使rN≤R,求取阵元位置 D=(d1,…,dN),满足约束 min其中dc为最小阵元间距,1≤j<i≤N,使该阵的峰值旁瓣电平(LPSL)最低.将该约束最优化问题描述为
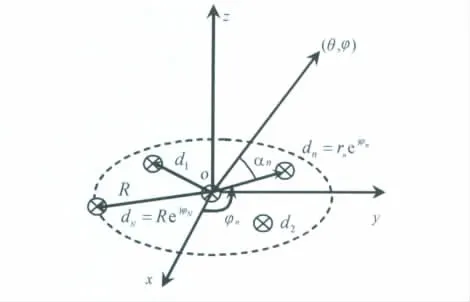
图1 稀布圆口径面阵的阵列结构
1.2 GA编码和适应度函数构造
取阵元位置矢量(d1,…,dN)作为上述最优化问题的决策变量,它是一个复向量,每个元素的模和相角用某一范围内的一个浮点数来表示,即所谓浮点数编码方法,又叫真值编码方法,其特点是编码使用决策变量的真实值,它不仅使遗传算法(GA)的变异操作能够保持更好的种群多样性,还克服了二进制编码方法运行性能差的缺点,使GA有较高精度和运算效率.
设阵元为全向性阵元,该平面阵列的方向图函数可以表示为[4]
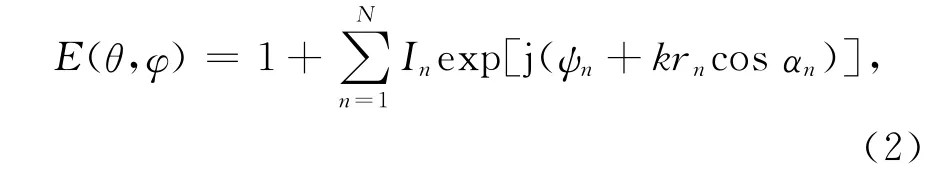
式中
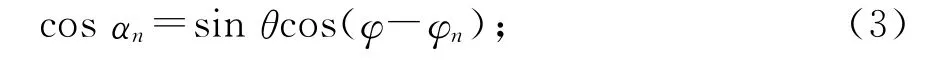
k=2π/λ,λ为工作波长;0≤θ≤π;0≤φ≤2π;所有阵元等幅同相激励,即取In=1,ψn=0取适应度函数为整个φ平面的旁瓣电平,则
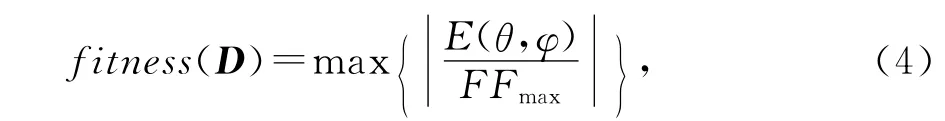
式中:FFmax为主瓣最大值;φ,θ所对应的范围为除主瓣外的所有旁瓣区域.最优化模型为
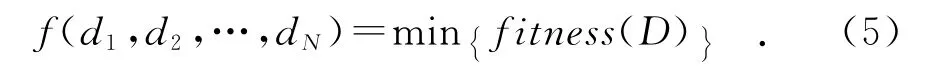
1.3 初始群体的创建
为了方便遗传算法的运用和充分利用约束条件下各阵元的布阵自由度,同时为了使创建的初始群体满足最小阵元间距约束,这里先构造用于间接描述个体的模板辅助矢量C.分析图2所示的半径相隔dc的均匀同心圆环阵列的阵元位置分布特性,并以此为基础来构造满足多个约束的可行解个体,再组建多个可行解个体组成的集合,从而构建初始群体.
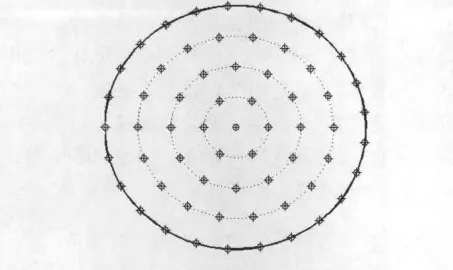
图2 均匀同心圆环栅格上布阵的均匀圆口径面阵
设图2所示的圆形阵列的口径为R=(a+1)dc,a∈Z.在半径相隔dc的均匀同心圆环栅格上,均布阵元间距不小于dc的尽可能多的阵元,这种阵元分布特性尽可能地运用了阵元的布阵自由度,同时满足优化约束|dm-dn|≥dc>0.取复矢量

为模板辅助矢量,它表示的阵列满足最小阵元间距约束.式中a=|R/dc|-1为栅格圆的数目,k1,k2,…,ka分别为第1,2,…,a层栅格圆上最多可以布置的阵元数目,Δ1,Δ2,…,Δa为第1,2,…,a层栅格圆上布置最多阵元数目时相位角坐标值的间隔.C与阵元间距约束和相角间隔约束有关,因而又称为约束矢量.如取最小阵元间距约束为dc=λ/2,可计算得到半径相隔dc均匀同心圆环的各栅格圆上的最多阵元数目和各栅格圆上阵元相位坐标值的最小间隔,如表1所示.
模板矢量Ft的构造方法如下:
1)生成所有元素均属于区间[0,0.5λ]的实随机列向量,其维数为并将该列向量的元素按行从小到大排序,得向量M0,设M0的第一节由第1行至第k1行的共k1个元素组成,第二节由第k1+1行至第k1+k2+1行的共k2个元素组成,依此类推,第a节有ka个元素,参见表1,第一节取k1=6个元素,第二节取k2=12个元素,以此类推.再将属于各节的元素按大小随机排列,得向量
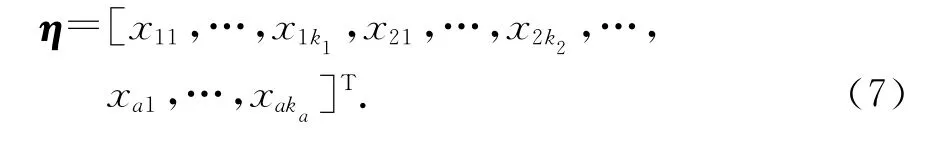
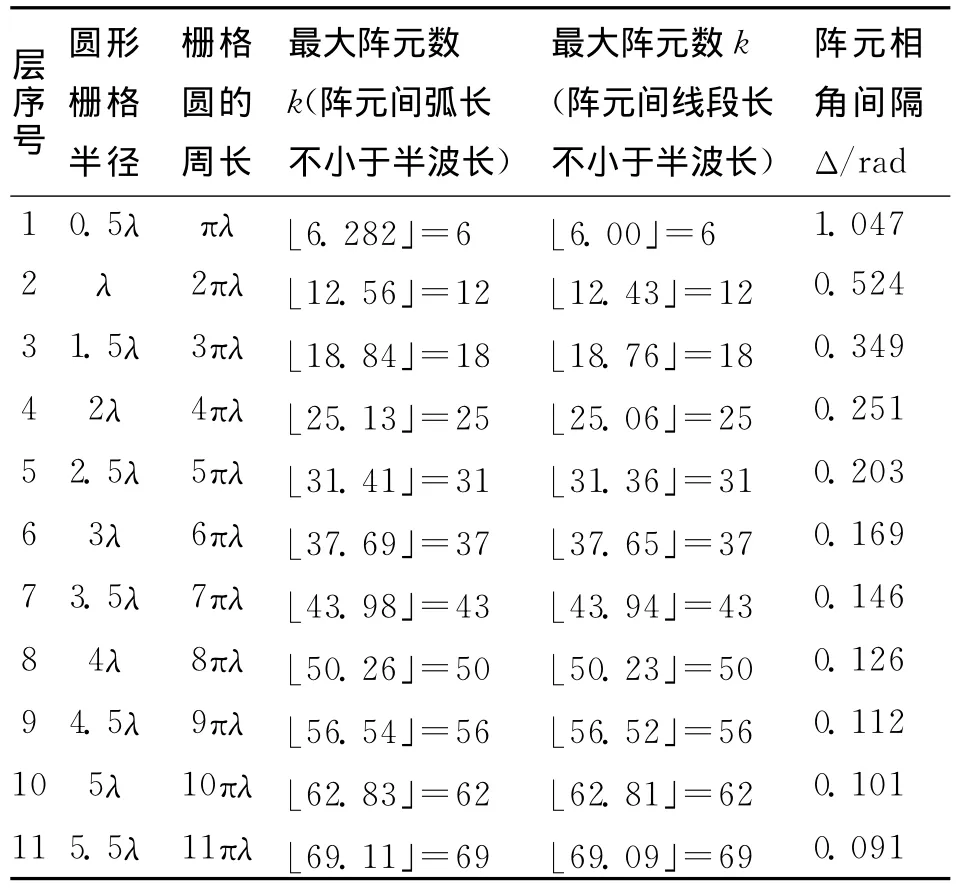
表1 各栅格圆上最大可能阵元数目及阵元相角间隔
该向量的特征是:节内元素是按大小随机排列的,且后一节的最小值元素不小于前节的任一元素,称其为η特性.
2)生成元素均属于区间[0,2π]的实随机列向量[ξ1,ξ2,…,ξa]T,然后将它扩展成
3)向量η的各元素作为模加到模板辅助向量C各对应元素的模;向量ζ的各元素作为相角加到模板辅助向量C各对应元素的相角,得模板矢量Ft,如式(9)所示为
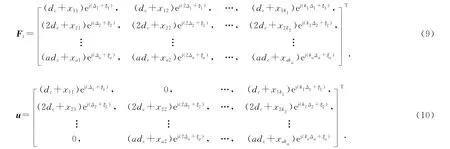
可以证明,以模板矢量Ft的各元素为阵元坐标的圆口径阵列满足两两阵元间距不小于dc.为了从模板矢量Ft得到阵元数目为N+1的个体矢量FA,下面定义个体索引矢量S:
定义1: 个体u由模板矢量Ft稀疏化处理而得,若Ft的第q个元素被稀疏,则对应的个体索引矢量S的第q个元素记“0”,若该元素被选取,则记为“1”,称S为对应于个体u的索引矢量.
若个体索引矢量S为
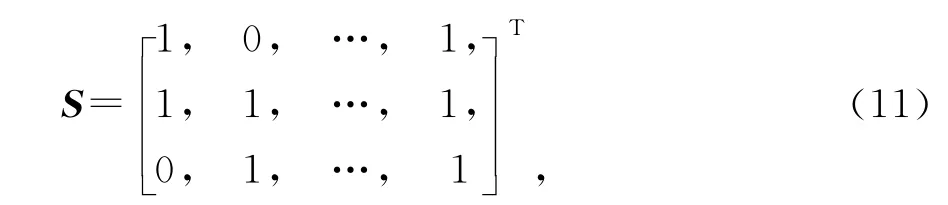
则对应的个体u如式(10)所示.
个体u与模板矢量Ft的关系表示为

即视Ft和S为数组,它们进行对应元素相乘的数组乘运算即得稀疏向量u,用它的非零元表示决策变量.
阵列的N个阵元坐标作为待优化的决策变量,从模板矢量(9)中随机索引出有N个非零元素的矢量u,不难将它的维数再扩展一维,用这一维表示圆口径中心的固定阵元的坐标,扩展后的稀疏向量记为FA.可以证明,FA表示的阵列是满足口径不大于R,阵元数为N+1且阵元间距不小于dc的一个可行解个体,它是由最小阵元间距约束dc、向量η,S和ζ间接表示的,遗传算法中,对个体FA直接进行遗传操作生成子代个体的过程,可以间接地由η,S和ζ等遗传信息进行遗传操作来代替.
生成M个形如u的个体,可以组成规模为M的初始群体U.容易证明群体U变换出的每个成员个体都是满足优化约束的可行解个体.这里,以群体U的每个个体索引向量为列向量的矩阵记为种群索引矩阵SM.
1.4 遗传操作预处理及后处理
该最优化中,标准GA的交叉算子和变异算子不能直接使用,原因是即使父代个体全部满足最小阵元间距约束,常规的交叉和变异也可能使子代个体成为不满足最小阵元间距约束的不可行解,使得优化过程无法继续.因此,需要修正交叉和变异算子,我们分别称修正后的交叉和变异算子为广义交叉算子和广义变异算子.同样为了避免优化过程中出现不可行解,这里还需要设计两个变换,第一,广义交叉和变异之前,需要一个变换从遗传群体中提取遗传信息(遗传预处理);第二,广义交叉和变异之后,需要一个逆变换由遗传信息重构遗传群体.
定义3: 以种群约束矩阵SM为索引从整体约束矩阵CA取得的元素所组成的M 列矩阵CM矩阵称为该种群的种群约束矩阵

定义4: 由形如U的父代群体U1得到遗传操作(广义交叉和广义变异)前的基因矩阵P的如下变换为遗传操作预处理:
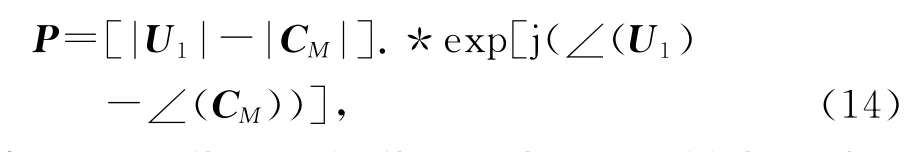
式中 :CM是种群U1的种群约束矩阵;||表示对矩阵的各元素取模得到模矩阵;∠()表示对矩阵的各元素取相角得到相角矩阵.
定义5: 由遗传操作(广义交叉和广义变异)后的基因矩阵P′得到子代群体U2的如下变换为遗传操作后处理:
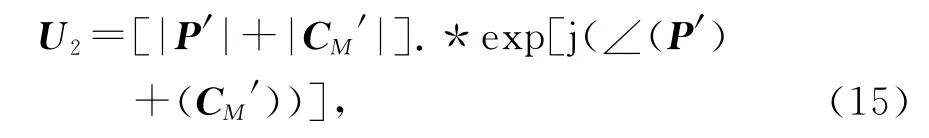
式中:P′是基因矩阵P经广义交叉算子和广义变异算子作用后得到的基因信息矩阵;CM′是对应于种群P′的种群约束矩阵.
1.5 广义交叉算子和广义变异算子
将遗传算法应用于约束最优化问题的关键是对约束条件的处理,可以按无约束问题那样进行交叉和变异操作,再检查是否违反约束,如果没有违反,则表明是可行解,否则就是不可行解.然而这样的处理实际上是行不通的(实际应用中计算量大,效率低),因为要找到一个可行解同样是很难的[11].这里需要设计新的交叉和变异算子来避免不可行解的出现.
新的交叉算子首先选定基因矩阵P的某两列,然后把随机选定的交叉位置上对应非零元素的模值进行交换,最后将得到的两个基因向量的模向量元素排序,方法是取出模向量,使它具备η特性:节内元素按大小随机排列,且后一节的最小值元素大于前节的任一元素.
新的变异算子旨在使表示遗传信息的索引矢量S突变,首先按变异概率随机选定需变异的基因矩阵P的某列,然后随机选定一个位置上的元素进行变异,若该元素为0,则用复数riejφi替代,模值ri取为该节内最大模值和最小模值之间的一个随机数,相角值φi变异为属于区间[0,2π]的随机数,且变异该元素所在节内的其他阵元的相角值等于该随机数.广义交叉算子和广义变异算子作用时保证非零元的个数始终为N,且使遗传信息矢量保持η特性和ζ特性.
经典遗传算法的交叉算子和变异算子作用的对象是个体的编码,而本文的广义交叉和变异的对象不再是真正意义上的个体编码,是父代群体析出的遗传信息S,η和ζ.另外,经过一般的交叉和变异操作后,还需对得到的遗传信息重新排序整理才得到有效的子代遗传信息S2,η2,ζ2.基于上述两方面的原因,本文称之为广义交叉算子和广义变异算子.
为了让子代个体遗传信息的模值元素满足η特性,本文采用如下的排序整理方法:首先找出遗传操作后子代遗传信息矢量的各节模值元素的最小值,然后从最后一节依次向前一节作排序处理,最后一节的元素不需处理.以第i节元素为例,设第i节元素的模最小值为a,将a与第i-1节的所有模元素比较,若第i-1节内的某模元素大于a,则用a替换该元素的模值.子代遗传信息矢量中的元素经过此广义遗传操作后得到了满足η特性和ζ特性的遗传信息向量P′,再经遗传后处理式(15),可以重构出由可行解个体组成的子代群体.
2 算法流程
在基本遗传算法(SGA)的算法流程中,本文改进了初始群体生成的方法,扩展了交叉和变异算子以及增加了遗传预处理和后处理,最终实现了本文的多约束综合问题的求解,具体的修正遗传算法的算法流程如图3所示.

图3 修正遗传算法流程图
3 仿真实例
以环间距为0.5λ、孔径为2λ的4层同心圆环均匀阵列为基础构造模板辅助矢量,由表1可知,模板辅助矢量的维数为61.设待优化的圆形阵列的孔径为2.5λ.优化约束为在孔径范围内的任意两阵元间距不小于0.5λ.设定稀布率为70%,即经过稀布优化后需布置的阵元数为42(口径中心固定的一个阵元不计).
利用本文介绍的修正遗传算法,选取式(4)为适应度函数,遗传算法的基本参数选取如下:种群体数为100,交叉、变异概率分别为0.7和0.01,进化代数为200.采取轮盘赌的选择方案,为保证收敛,采用了最佳保留选择机制.为检验本文所提方法的稳健性,独立地进行了5次仿真试验.最差和最好仿真实验结果得到的峰值旁瓣电平分别为-20.797dB和-19.838dB.表2给出了最优个体向量,图4是经过综合后得到的最优个体对应的方向图,图5是其在φ=0°,φ=45°,φ=90°截平面的波束图,图6是最优个体的阵元布置图.
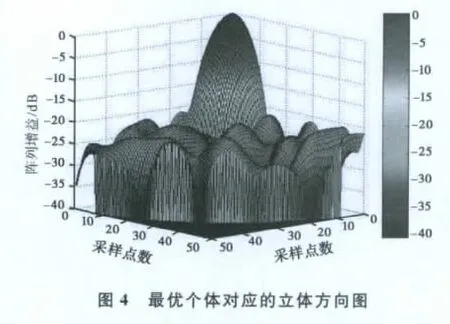
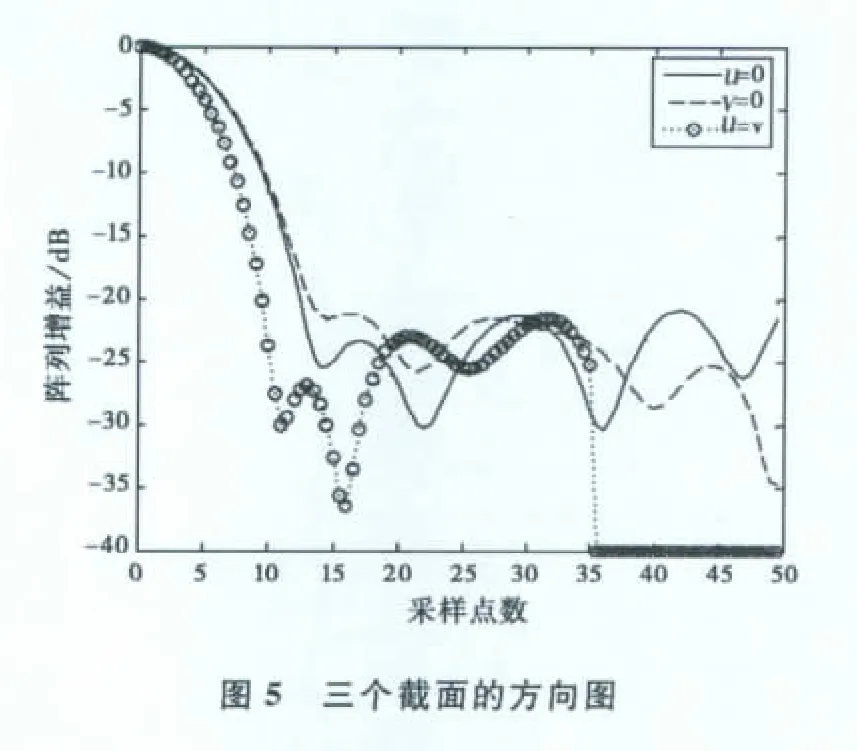
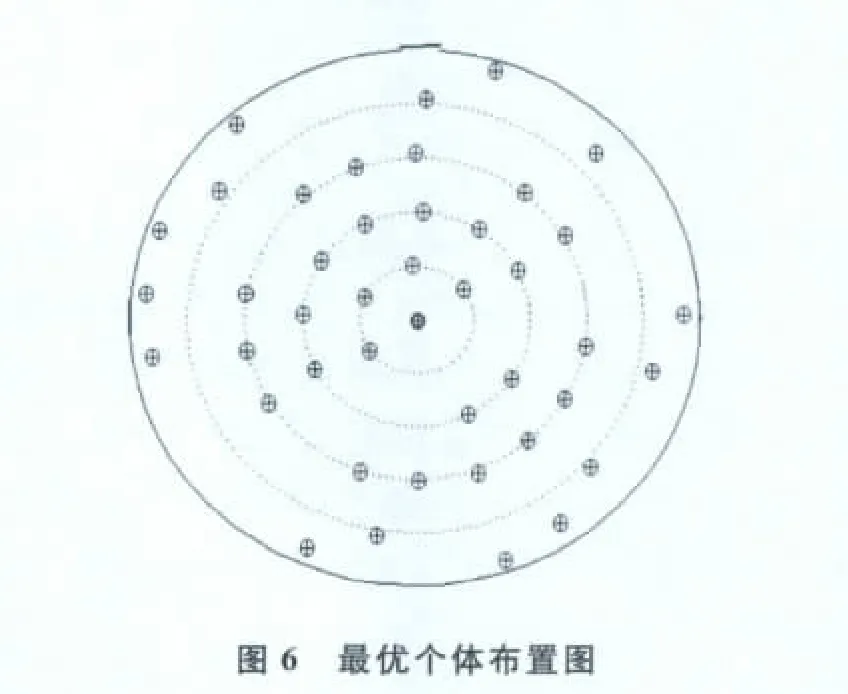
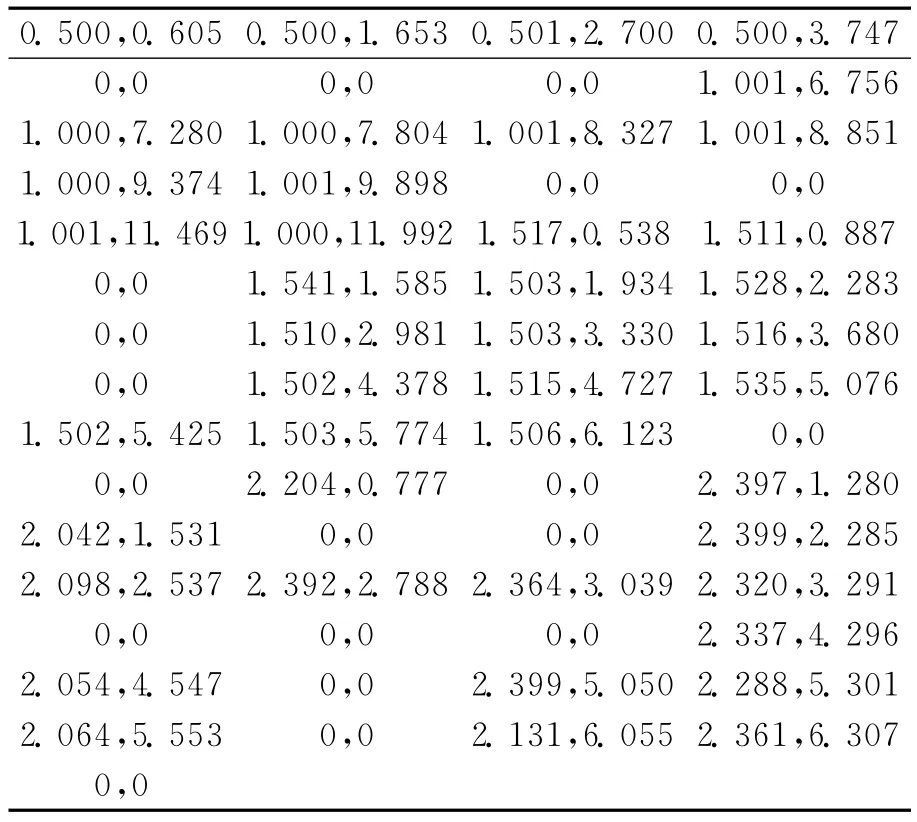
表2 最优个体阵元坐标(第一元素是模值,第二元素是相角)
4 结 论
对于圆形稀布阵列,阵元位置的设计需进行复杂的数值优化计算.基于改进的实数遗传算法,文中提出了一种综合有阵元数、孔径和最小阵元间距约束的圆形口径稀布面阵的新方法.采用新的编码方法,使间接描述的优化变量适用于修正的实数遗传算法,设计的广义遗传操作、预处理和后处理使得遗传算法在优化过程中不再需要去校验每个个体解的可行性,显著地提高了优化效率.该方法将稀布圆阵的综合从规则栅格的稀疏约束拓展为最小阵元间距约束,最小阵元间距可以事先依据阵元间的互耦情况设定,算法有很强的有效性和稳健性,因此该方法相对于经典的遗传算法能更大程度地满足实际工程设计的需要.
[1]RAHIM T,DAVIES D E N,ENG F.Effect of directional elements on the directional response of circular antenna arrays[J].IEE Proc,1982,129(1):18-22.
[2]GOTO N,TSUNODA Y.Sidelobe reduction of circular arrays with a constant excitation amplitude[J].IEEE Trans Antennas Propag,1977,25(6):896-898.
[3]REED J H.Software Radio:A Modern Approach to Radio Engineering[M].Upper Saddle River:Prentice Hall,2002.
[4]JARSKE P,SARAMAKI T,MITRA S K.On properties and design of nonuniformly spaced linear arrays[J].IEEE Trans Acoustics Speech and Signal Processing,1988,36(3):372-380.
[5]HAUPT R L.Thinned arrays using genetic algorithms[J].IEEE Trans Antennas Propagat,1994,42(7):993-999.
[6]KUMAR B P,BRANNER G R.Generalized analytical technique for the synthesis of unequally spaced arrays with linear,planar,cylindrical or spherical geometryp[J].IEEE Antennas and Propagation,2005,53(2):621-634.
[7]KUMAR B P,BRANNER G R.Design of unequally spaced arrays for performance improvement[J].IEEE Trans Antennas Propag,1999,47(3):511-23.
[8]陈客松,何子述.平面稀布天线阵列的优化算法[J].电波科学学报,2009,24(2):193-198.CHEN Kesong,HE Zishu.Synthesis approach for sparse plane arrays[J].Chinese Journal of Radio Science,2009,24(2):193-198.(in Chinese)
[9]CHEN Kesong,HE Zishu,HAN Chunlin.A modified real GA for the sparse linear array synthesis with multiple constraints[J].IEEE Trans Antennas Propag,2006,54(7):2169-2173.
[10]CHEN Kesong,YUN Xiaohua,HE Zishu,et al.Synthesis of sparse planar arrays using modified real genetic algorithm[J].IEEE Trans Antennas Propag,2007,55(4):1067-1073.
[11]王小平,曹立明.遗传算法—理论、应用与软件实现[M].西安:西安交通大学出版社,2002:108-109.
[12]闫玉波,崔玉国,焦培南.基于副瓣峰值控制的天线阵方向图综合[J].电波科学学报,2009,24(2):249-253.YAN Yubo,CUI Yuguo,JIAO Peinan.Pattern Synthesis of antenna arrays based on control of peak sidelobes[J].Chinese Journal of Radio Science,2009,24(2):249-253.(in Chinese)
[13]柴焱杰,孙继银.平面波在时域有限差分法中的引入方法研究[J].电波科学学报,2011,26(2):388-392.CAI Yanjie,SUN Jiyin.Importing methods of plane wave in the finite difference time domain method[J].Chinese Journal of Radio Science,2011,26(2):388-392.(in Chinese)
[14]CAORSI S,LOMMI A,MASSA A,et al.Peak sidelobe level reduction with a hybrid approach based on gas and difference sets[J].IEEE Trans Antennas Propag,2004,52(4):1116-1121.
[15]HAUPT R L.Unit circle representation of aperiodic arrays[J].IEEE Trans Antennas Propag,1995,43(10):1152-1155.
[16]VESCOVO R.Constrained and unconstrained synthesis of array factor for circular arrays[J].IEEE Trans Antennas Propag,1995,43(12):1405-1409.

