雷电电磁脉冲三维磁场测量系统研究

周璧华 马洪亮 李 皖 徐 云 丁雅菲

（解放军理工大学 电磁环境效应与电光工程国家重点实验室，江苏 南京210007）

引 言

对地闪放电电流的测量，除了可采用在高塔上安装分流器或Rogowski线圈的方法［1-2］以外，通过在地面测量放电电流电磁辐射产生的雷电电磁脉冲（Lightning Electromagnetic Pulse，LEMP）磁场和对雷击点及放电通道定距，可实施对地闪雷电流的间接测量 .鉴于一对放置在地面上的正交线圈既可用于LEMP磁场的测量，又可为地闪放电电流定向，故可作为地闪雷电流间接测量的首选.考虑到自然界的闪电分为云闪和地闪，地闪所占比例不到1/3，对所测LEMP磁场到底是不是地闪产生的，需加以鉴别.此外，受加工工艺的限制，正交线圈的制作未必能达到真正正交，如何对线圈处于非理想正交情况下的测试结果进行修正也是需要研究的.为此本文专门设计制作了用于测量LEMP三维磁场的大型三维正交线圈及测量系统；推导了三维磁场的计算式；对系统进行了时域标定，针对标定中发现的波形失真和三维正交线圈的非理想正交问题，分别给出了波形的矫正方法和数据的修正方法.采用本测量系统，在年内的自然雷观测中获得大量数据，根据三个正交方向磁场的实测结果，首先通过对三线圈所测磁场大小的比较，判定是否由地闪产生，然后经波形矫正、非理想正交数据修正和向量合成计算得出磁场波形.同时根据雷声定距结果，确定了测点与雷电放电通道的距离，完成了地闪雷电流的间接测量.最后，采用间接测量得出的雷电流波形和测点与放电通道的距离，对测点处的磁场进行了数值模拟，计算结果表明，得出的LEMP磁场波形及量值与实测结果一致性较好.

1 三维磁场测试系统简介

1.1 测量系统的组成

雷电电磁脉冲三维磁场测量系统由大型三维正交线圈、光隔离信号传输系统和信号采集处理终端三部分组成，其系统框图如图1所示.

图1 正交环天线测量系统框图

用于接收LEMP三维磁场信号的装置由三个相互正交的线圈组成，如图2所示.每个线圈均采用内外导体结构，其中内导体即线圈，为带有绝缘外皮的铜线，接地的外导体为开隙钢管，内导体的接线从间隙处引出.这样的设计不但可利用钢管屏蔽测点处电场对磁场测量的干扰，而且因钢管开有间隙不能形成导电环路，从而确保管内铜线线圈对磁场信号的接收，此外钢管还能起线圈支架的作用，坚固耐用.

图2 LEMP三维磁场测量装置前置部分照片

为避免三维正交线圈接收的信号在传输过程中受到干扰，信号的传输采用了光隔离系统，正交线圈输出的信号经积分处理和放大后再通过非线性校正、放大与补偿，由光发射机将电信号转换为光信号，经全介质光缆传输至光接收机，再将光信号转换为电信号，经放大补偿后，最终由数字示波器进行采集、记录.

1.2 LEMP三维磁场测量系统的定向原理

将图2所示的LEMP三维磁场测量线圈置于三维直角坐标系中，其x轴、y轴、z轴的正向分别指向正南、正西和竖直向上.称位于xoz平面、yoz平面和xoy平面的三个正交线圈依次为1号线圈、2号线圈和3号线圈，如图3所示.

图3 三正交线圈放置方位

设闪电发生时，闪电回击通道与xoy平面的夹角为α，通道在xoy平面上的投影与x轴正向的夹角为β，如图4所示.

假设1、2、3号线圈测得的磁场强度分别为H1（t）、H2（t）、H3（t），则方位角计算公式为：

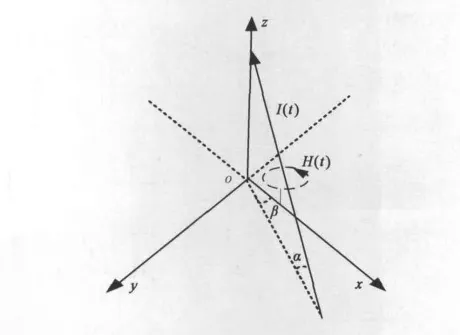
图4 闪电回击通道方位

已知α和β，结合线圈感应电压的极性可确定放电通道的方向.

2 LEMP三维磁场测量系统的标定

测量前，必须将测量系统的前置部分放置在LEMP磁场的模拟环境中进行标定.标定系统布局如图5所示，在8m高的楼顶和大地之间架设了一根垂直于地面的粗铜线，其下端通过接地体良好接地，上端接PrimaSUG 61005B型雷击浪涌发生器，以产生瞬变电流，模拟地闪放电通道 .在导线上，套上标准的Rogowski线圈用以测量模拟闪电通道中的电流波形.同时以该垂直导线为轴，在地面相对于模拟放电通道不同角度上14.8m径向距离处放置所研制的三维磁场测量线圈.并通过光隔离系统将测得的信号传输至控制室内，对被测磁场信号进行采集和记录.

图5 LEMP磁场测量系统标定现场示意图

以1号线圈系统为例，根据标定数据绘制的标定曲线如图6所示，得出标定系数k1＝11.52 A·V-1·m-1.同样，得出的2号线圈和3号线圈系统标定系数k2＝12.93A·V-1·m-1，k3＝7.38 A·V-1·m-1.

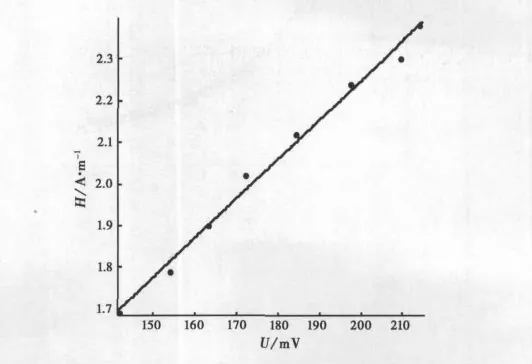
图6 1号正交环标定曲线

注意到三个线圈输出的电压波形都存在同样的低频失真，故必须对所测的磁场波形进行矫正.

这里采用输出误差系统辨识模型［3-4］对失真波形进行矫正，选用的矫正滤波器系统函数为矫正后的磁场波形如图8所示.

由图8可见，波形矫正效果较好，故可利用该模型对线圈测得的波形进行矫正.

图7 电流波形与测得磁场波形对比

图8 矫正后磁场波形

3 非正交性误差分析及其修正［5-7］

如前所述，本文专门设计制作了用于测量LEMP三维磁场的大型三维正交线圈，提高线圈之间“正交的程度”是其目的之一.实际上受限于线圈骨架加工精度，“正交”总还存在误差，这将导致三维磁场测量的偏差.为此，需要对线圈间的几何关系进行实际测量，通过定量分析给予修正.

如图9所示，设理想正交的三个线圈平面的法向分别为ox，oy，oz；输出的磁场脉冲峰值为Hx，Hy，Hz.对应非理想正交的三个线圈的法向分别为ox1，oy1，oz1；输出的信号为 Hx1，Hy1，Hz1.使oz轴与oz1轴重合（实测时可保证3号线圈处于真正水平状态），且坐标面yoz与y1oz1共面，并假设oy1与oy夹角为λ，轴ox1与xoy平面的夹角为θ，与zox面夹角为γ.

图9 实际与理想磁场测量装置三轴关系

分别将 Hx，Hy，Hz投影到ox1，oy1，oz1轴上，各量值之间的相互关系如下：

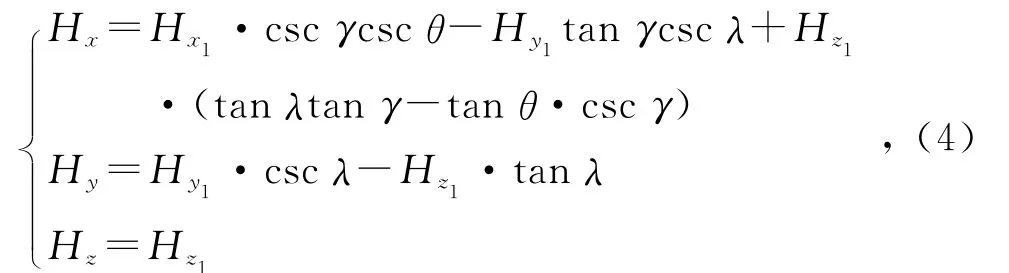
式中θ，λ，γ可正可负，通过实测得到本装置的θ，λ，γ数值为1.3°，0.7°，-2.1°.

假设理想正交线圈磁场测量装置测到的磁场强度矢量为H＝（Hx，Hy，Hz），实际磁场测量装置测到的磁场强度矢量为 H1＝（Hx1，Hy1，Hz1），则 H与H1的变换关系为

式中：

4 实测结果分析

以2012年8月21日16：21′12″在南京地区测到的一次闪电过程为例，实测波形如图10所示.共发生4次回击，整个闪电放电过程持续时间300 ms，雷声声源定距系统显示声光差数据为3.7s，声速取为350m/s，算得雷击点与观测点的水平距离r为1 295m.

首先，采用上述输出误差系统辨识模型对三线圈测得的首次回击磁场失真波形进行矫正，以南北方向磁场矫正前后的波形为例，如图11所示.

图10 120821162112号磁场波形

经矫正及其修正后的三个方向上的磁场波形如图12所示，图中三个波形走势基本相同，但置于水平方向上的3号线圈测得的磁场强度很小，可忽略不计.大致判断所测得的磁场波形是由地闪放电电流产生的，经计算雷击点位于南偏东57.8°.

将三个正交线圈测得的磁场分量进行向量合成得到总的磁场波形，并利用式（7）双指数函数进行拟合，合成的波形与原波形对比情况如图13所示.

图13 采用双指数函数拟合的水平磁场波形

式中：H0＝2.3A/m；k＝1.1；α＝1.7×104s-1；β＝6.4×105s-1.

考虑到LEMP水平磁场在地面附近传播过程中除遇有铁磁介质的情况外，一般不会受到大的影响，故这里按安培环路定律，由正交线圈测得的合成磁场强度求取雷电流

为了验证式（8）得出的雷电流，下面对该电流产生的LEMP磁场进行数值模拟［9-11］.近似认为地闪回击放电通道不分叉且垂直于地面，通道周围为无穷空间，采用时域有限差分（Finite-Difference Time-Domain，FDTD）法计算测点处的水平磁场.计算中回击电流选用MTLE模型，回击通道高度取D＝5 000m，考虑到放电通道辐射场各分量相对放电通道轴对称，采用改进的一阶Mur吸收边界条件，在二维柱坐标下建立计算LEMP各场量的差分方程，网格划分取为1m×1m，时间步长Δt＝1/6×10-8s，大地电参数εrg＝10，σg＝10-3S/m，仿真得到的磁场波形如图14所示.由图可见，数值模拟结果与实测磁场波形具有较好的一致性.可见，在已知测点处磁场和测点与电流源距离的情况下，可按安培环路定律计算雷电流.这就为雷电流的间接测量提供了一种可行的手段.

图14 实测结果与仿真结果对比

2012年8月份共测得53次闪电产生LEMP三维磁场波形，表1列出了其中10次闪电磁场波形的数据统计结果.表1的数据按实测时刻编号，如与12∶39′44″对应的编号即为123944.

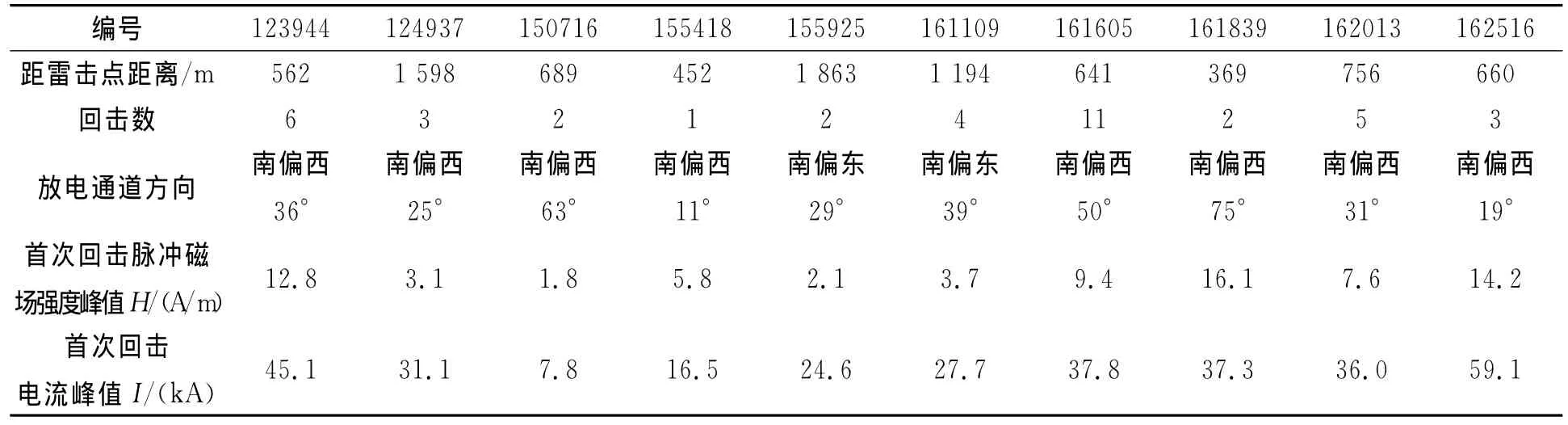
表1 2012年8月21日测得的LEMP磁场波形特征参数

5 结 论

本文为实现地闪雷电流的间接测量，设计制作了一套大型LEMP三维磁场测量系统，在LEMP磁场的模拟环境中进行了时域标定和实验研究.提出了线圈测量磁场导致低频失真的矫正方法、三正交线圈并非理想正交带来误差的修正方法.对采用该系统测得的自然雷波形进行了数据处理、统计和分析.根据所测三维磁场峰值大小，可大体判断云闪和地闪.利用所测数据，结合磁定向法和声光差定距法，可确定雷击点的方位和距离，从而实现了对地闪雷电流的间接测量.采用由实测数据间接获得的雷电流波形、测点与放电通道的距离，经数值模拟得出的LEMP磁场时间特性与实测结果一致性较好.

［1］高 成，石立华，陈 斌，等.高塔直击雷雷电流全波检测系统［J］.电波科学学报，2000，15（3）：278-284.GAO Cheng，SHI Lihua，CHEN Bin，et al.Fullwaveform measuring system for lightning current caused by lightning strikes to tall structures［J］.Chinese Journal of Radio Science，2000，15（3）：278-284.（in Chinese）

［2］RAY W F，HEWSON C R.High performance Rogowski current transducers［C］//IEE Industry Application Confer.Rome，2000，5：3083-3090.

［3］LJUNG L.System Identification：Theory for the user［M］.2nd ed.Beijing：Tsinghua University Press，2002.

［4］GUERRIERI S，NUCCI C A，RACHIDI F，et al.On the influence of elevated strike objects on directly measured and indirectly estimated lightning currents［J］.IEEE Transactions on Power Delivery，1998，13（4）：1543-1555.

［5］殷 勤，陈 彬，汪 莹，等.电磁跟踪系统磁传感器三轴非理想正交的快速校正算法［J］.系统工程与电子技术，2011，33（8）：1698-1702.YIN Qin，CHEN Bin，WANG Ying，et al.Fast calibration arithmetic for incompletely orthogonal threeaxis magnetic sensor of electromagnetic tracking system［J］.Systems Engineering and Electronics，2011，33（8）：1698-1702.（in Chinese）

［6］黄学功，王 炅.地磁信号检测系统误差分析与补偿方法研究［J］.兵工学报，2011，32（1）：33-36.HUANG Xuegong，WANG Jiong.Error analysis and compensation methods for geomagnetic signal detection system［J］.Acta Armamentarii，2011，32（1）：33-36.（in Chinese）

［7］周榕军，刘大明，洪泽宏，等.非理想条件下三轴磁通门传感器误差修正方法［J］.舰船科学技术，2011，33（3）：85-89.ZHOU Rongjun，LIU Daming，HONG Zehong，et al.Fast calibration arithmetic for incompletely orthogonal three-axis magnetic sensor of electromagnetic tracking system［J］.Ship Science and Technology，2011，33（3）：85-89.（in Chinese）

［8］张飞舟，陈亚洲，魏 明，等.雷电电流的脉冲函数表示［J］.电波科学学报，2002，17（1）：51-53.ZHANG Feizhou，CHEN Yazhou，WEI Ming，et al.Representing the lightning current by pulse function［J］.Chinese Journal of Radio Science，2002，17（1）：51-53.（in Chinese）

［9］RAKOV V A，UMAN M A.Review and evaluation of lightning return stroke models including some aspects of their application［J］.IEEE Trans Electromagn Compat，1998，40（4）：403-426.

［10］RACHIDI F，NUCCI C A.On the Master，Uman，Lin，Standler and the modified transmission line lightning return stroke current models［J］.J Geophys Res，1990，95：20389-20394.

［11］NUCCI C A，MAZZETTI C，RACHIDI F，et al.On lightning return stroke models for LEMP calculations［C］// Proc 19th Int Conf Lightning Protection.Graz，April，1988.