基于广义似然比检验-动态规划的检测前跟踪算法

战立晓 汤子跃 易 蕾 朱振波

（1.空军预警学院研究生管理大队，湖北 武汉430019；2.空军预警学院空天基预警装备系，湖北 武汉430019）

引 言

隐身技术的运用，使得几何尺寸较大的作战武器如战斗机、轰炸机等成为雷达探测领域的“低可探测目标”，对雷达提出了严峻的挑战.如何提高雷达对微弱目标信号的检测已成为现代雷达急需解决的关键问题.

检测前跟踪（TBD）技术［1-7］是一种低信噪比（SNR）背景下同时完成微弱目标检测和航迹处理的技术.它以时间换取能量，并不在每一帧完成目标是否存在的判决（传统的检测策略），而是通过联合处理M（＞1）个连续帧周期的数据，得到估计目标航迹的同时完成目标的判决.

TBD的先期研究主要聚焦于慢、小运动目标在红外和光学成像中的检测，如文献［8］提出的三维（空间和时间）匹配滤波来检测沿直线航迹运动的小目标，文献［9］提出的递归运动目标指示（MTI）算法检测小运动目标.但以上方法都需要已知目标的速度信息，若目标速度不匹配则检测效果较差.文献［1］提出的动态规划（DP）方法不需要已知目标速度信息，且TBD性能较好.文献［10］提出了一种基于强复杂噪声背景的红外微弱运动目标集成检测算法，该算法对各种加性、乘性噪声的滤波性能优异且均衡，适合对复杂噪声进行滤波.但以上方法的适用范围仅局限在红外和光学成像中对慢、小运动目标的检测.

文献［11］和［12］把TBD思想引入到雷达系统中，雷达中的目标检测不同于光学中的目标检测，雷达监视范围广且探测的目标速度大，从而TBD实现的复杂度更高.以往TBD算法的误差分析都是基于Cramer-Rao界，且与门限无关，文献［13］研究了雷达目标TBD算法中基于Barankin界的SNR门限影响问题.文献［14-16］深入研究了机载相控阵雷达中基于空时数据的自适应目标检测和航迹处理技术，该方法结合空时自适应处理（STAP）技术和广义似然比检验（GLRT）可以达到很好的检测性能.

针对一般的地面脉冲多普勒（PD）体制雷达，提出了一种距离多普勒域基于GLRT-DP的TBD算法.

1 基于GLRT的TBD算法

1.1 目标回波信号模型

假设目标判决之前积累M帧接收数据（即目标被照射M次），记为P＝［P1，…，PM］，一般的状态向量Pm属于四维向量空间 ［τm，fm，θm，φm］T，其中m＝1，…，M，τm为第m次照射时目标的时延（对应于目标的距离），fm为第m次照射时目标的多普勒频移（对应于目标的相对径向速度），θm为第m次照射时目标所在的方位角，φm为第m次照射时目标所在的俯仰角.为了简化，我们只考虑距离和多普勒两维坐标，即Pm＝［τm，fm］T.对于考虑方位角和俯仰角的情况只需增加向量的维数即可，不影响推导的一般性.

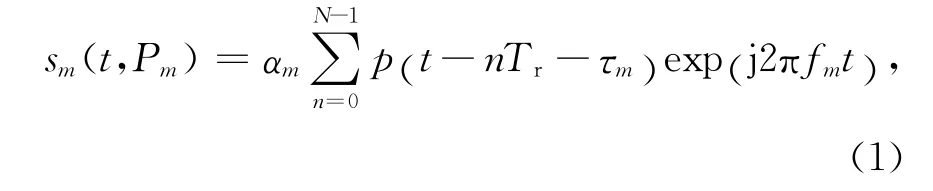
式中αm为目标回波信号幅度，记α＝［α1，…，αM］.假设αm满足Swerling I型目标模型，即在帧间起伏变化.

1.2 基于GLRT的TBD算法

在雷达监视区域内判决是否有目标，可以等效为解决下面的二元假设检验问题：

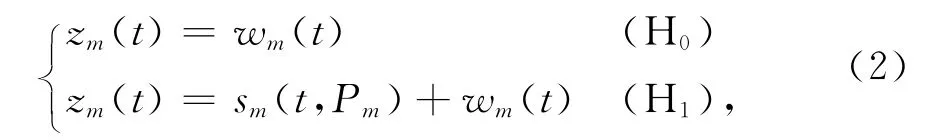
式中wm（t）为零均值加性复高斯白噪声，其功率谱密度为N0.在式（2）中，若H0成立，则判决为无目标；若H1成立，则判决为有目标.

由于α和P为未知参量，故式（2）为二元复合假设检验问题，通过GLRT的方法实现，即

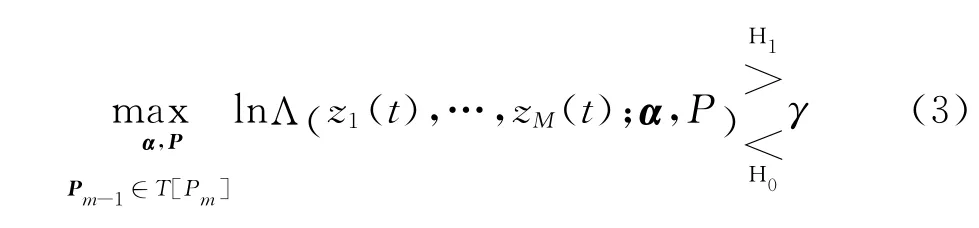
式中T［·］为状态转移函数，若给定了第m帧的状态向量Pm，则根据连续帧周期照射之间目标的运动规律可确定第m-1帧的状态向量Pm-1，该函数的实际结构依赖于目标运动的先验知识；γ为检测门限，可由预期的虚警概率Pfa计算得到，Pfa定义为H0为真时判决为H1的概率，即Pfa＝P（H1H0）；Λ是含有未知参量的似然比（LR），定义为

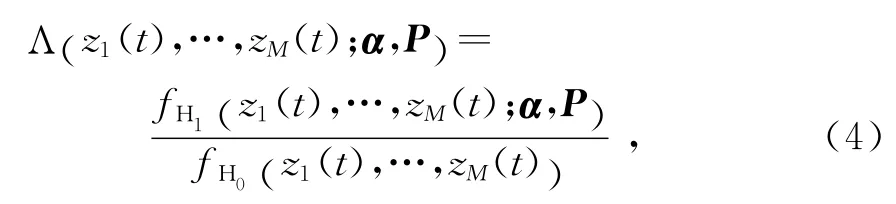
式中fH1（·）和fH0（·）分别为假设H1和H0对应的接收回波信号的概率密度函数（PDF）.

式（3）中的信号模型为连续时间信号模型，为便于处理，下面对其进行离散化.定义第m帧的单位能量函数为

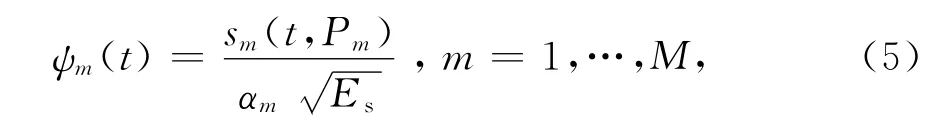
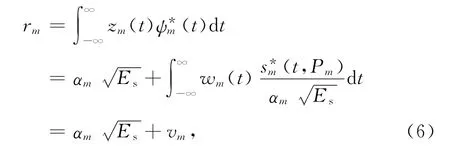
表示一组复高斯随机变量，其方差表示为

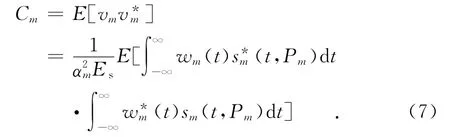
接收基带回波信号离散化后，基于GLRT的TBD算法表达式为

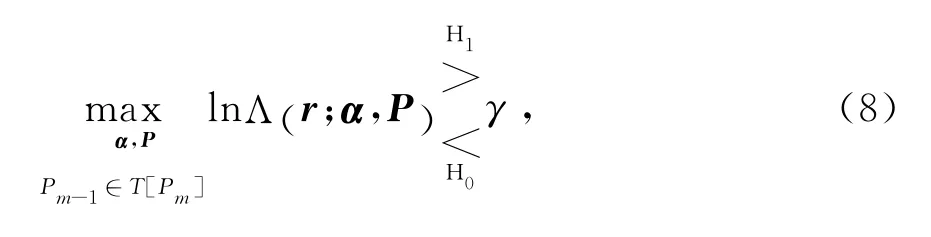
式中r＝［r1，…，rM］，且有

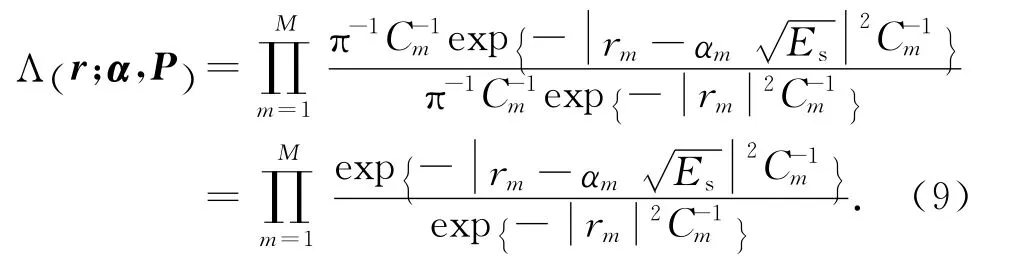
在式（9）中通过最大似然估计（MLE），去掉未知目标幅度α，即令下式为零

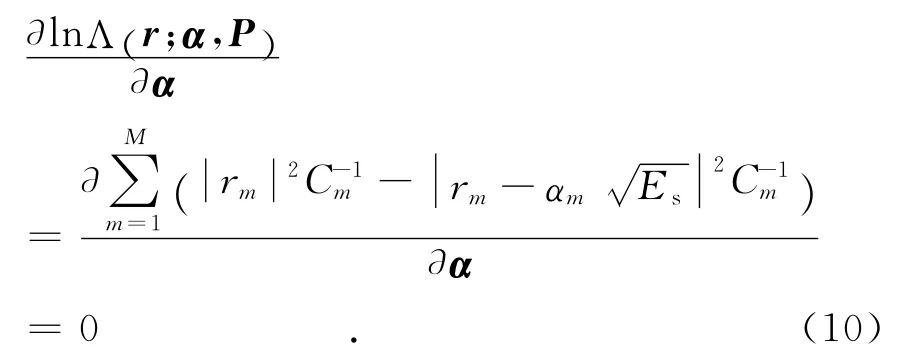
解得

把式（11）代入式（8）简化为

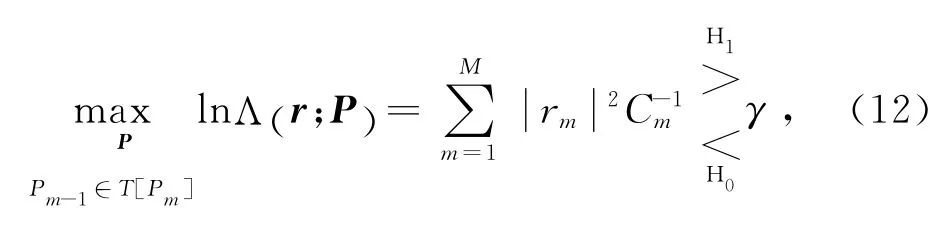
又Cm＝E［vmv＊m］＝N0，式（12）可进一步简化为

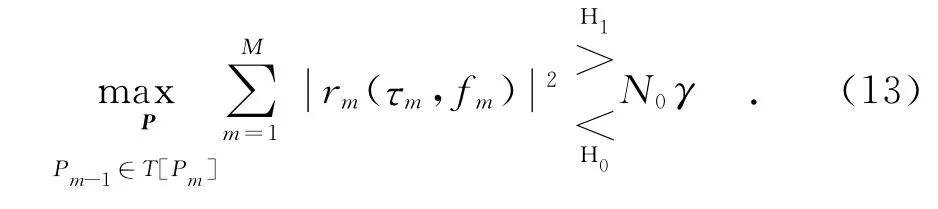
2 基于GLRT-DP的TBD算法

2.1 DP算法基本原理

DP法是解决多阶段决策过程最优化问题的一种方法.该方法针对多阶段决策问题的特点，把多阶段决策问题表示为一系列单一阶段问题，即把一个M变量问题转化为M 个同类型的一族单变量子问题而逐个加以解决.该方法利用状态变量来描述过程的演变，状态变量的取值称为状态，状态的取值集合称为状态集合.状态和状态集合都依赖于阶段m，分别记为xm和Xm.当各阶段状态和终状态确定后，该过程就完全确定，即可以表示为状态序列｛x1，x2，…，xM｝，其中x1为初始状态，xM为终状态.

对于给定的最优化过程，在各个阶段要选择变量的值使得全过程按给定的准则达到最优，各阶段中状态变量的选择就是问题的决策.一般用决策函数um（xm）表示决策过程.整个决策过程相对应的决策函数序列称为策略.决策过程还必须有一个度量其策略好坏的准则，称为指标函数.于是问题可归结为选择一个m阶段的策略使指标函数最大，其表示式为

式中：Im（xm）是从初始状态x1到状态xm的积累指标函数；vm为m个阶段的值函数，且其可以表示为

式中wi（xi，ui）是阶段指标，表示第i个阶段状态xi作出决策ui时的阶段指标函数.根据最优性原理可得

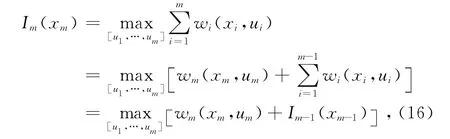
其中m＝2，3，…，M，表示决策过程划分的阶段数.

一般的，初始条件可以假设为

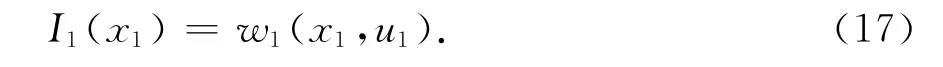
式（16）和式（17）就是多阶段决策过程的动态规划基本方程，这实际上是一个递推关系式.

2.2 DP法实现所提算法

我们把通过DP法来实现离散距离多普勒域基于GLRT的TBD算法简记为基于GLRT-DP的TBD算法，其中每一帧划分为一个阶段.该算法的步骤如下：

Step1：初始化.当m＝1时，即对应第1帧观测数据，对其每个距离多普勒分辨单元，定义积累指标函数为I1（P1），J1（P1）记录第1帧目标所在的距离分辨单元和多普勒分辨单元，公式为

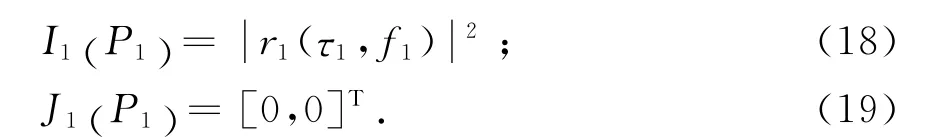
Step2：递归积累.当2≤m≤M时，对第m帧的所有距离多普勒分辨单元，有

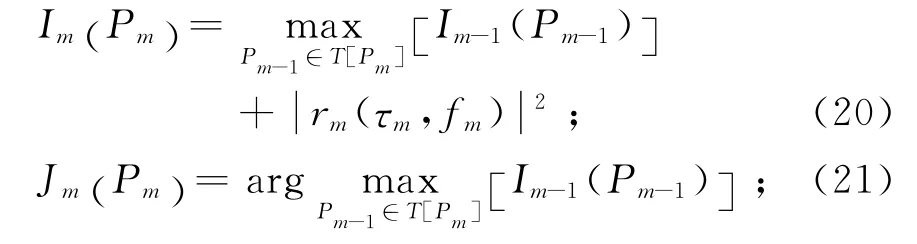
式中：Im（Pm）为第m帧积累指标函数；Jm（Pm）为航迹回溯函数，用于记录每一帧目标所在的距离分辨单元和多普勒分辨单元.

Step3：目标判决.依据式（13）进行门限判决

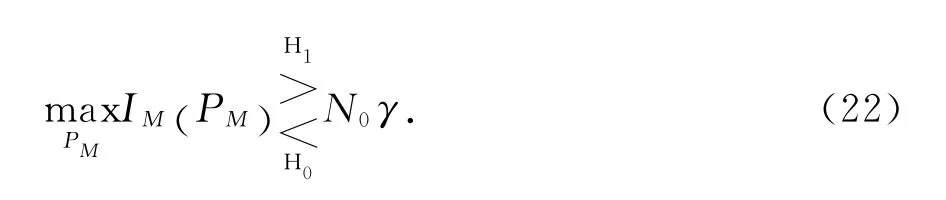
若H1成立，则判决为有目标，且得到估计值M；若H0成立，则判决为无目标.

2.3 算法运算量及性能分析

DP法运算量要比穷举法运算量低的多，因为它将一个M维的优化问题分解成为M 个二维问题.每一帧的回波接收数据，共有Nr个距离单元，N个多普勒单元，即由NrN个距离多普勒搜索单元组成.对于M帧接收数据，则共有（NrN）M个距离多普勒搜索单元.对于这样一个离散距离多普勒域的搜索寻优问题，穷举法的运算复杂度为O［（NrN）M］，而DP法的运算量随M 线性增加，其运算复杂度只有O［MNrN］，可见DP法的运算量优势明显.

依据式（22）的目标检测判决式，对其检测性能进行分析.因为检验统计量在两个假设下的PDFfH1（·）和fH0（·）难以求出，故论文采用Monte Carlo仿真的方法来计算虚警概率Pfa和检测概率Pd，其中Pfa在1.2节已定义，Pd定义为H1为真时判决为H1的概率，即具体的数值分析见下节仿真实验.

3 仿真实验及分析

仿真参数设置如下：仿真中的雷达为地面PD体制雷达，载频为1GHz，脉宽Tp＝0.2μs，脉冲重复频率fr＝800Hz，帧内相参积累脉冲数N＝32，即对应32个多普勒分辨单元，积累帧数M＝30，αm在帧间起伏变化，符合Swerling I型模型，距离分辨单元Nr＝300个，加性复高斯白噪声wm（t）～CN（0，2）.

图1给出了距离多普勒域中不同SNR时的第11帧接收回波数据，其中图1（a）和（b）中接收回波数据相参积累前SNR分别为0dB和-7dB，需要说明的是仿真实验中每帧接收回波数据中有32个脉冲相参积累，故相参积累后SNR为积累前SNR加上10lg（32）≈15dB.目标所在的距离多普勒单元为（147，14）.从图中可以看出，当SNR为RSN＝0dB时，目标可以明显被检测出来；而当SNR为RSN＝-7dB时，目标完全淹没在噪声当中，无法检测.

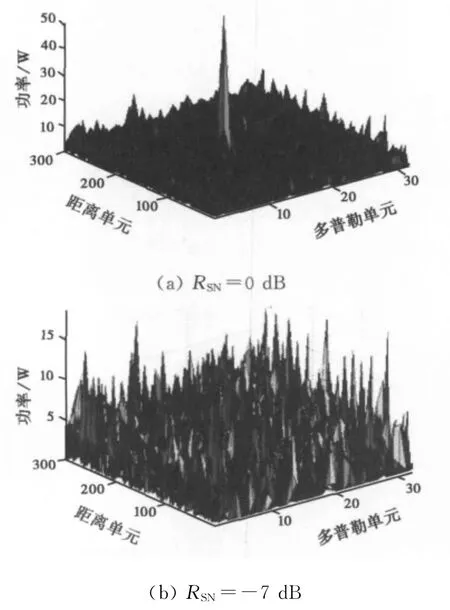
图1 距离多普勒域中不同SNR时第11帧接收回波数据

由图1可知，对于低SNR背景下的雷达目标检测问题，当SNR为-7dB时根据单帧数据完成目标判决已不可行，所以必须采用多帧积累的TBD技术.下面针对基于GLRT-DP的TBD算法进行相关仿真实验.

首先研究检测门限γ的设置问题.图2给出了虚警概率Pfa与检测门限γ之间的关系曲线，由于理论计算复杂，通过 Monte Carlo仿真实验得到，Monte Carlo仿真次数为100/Pfa次.由图2可知：随着门限的增高，虚警概率越来越低，例如虚警概率Pfa＝10-1时对应的门限γ＝170，而虚警概率Pfa＝10-4时对应的门限γ＝180.

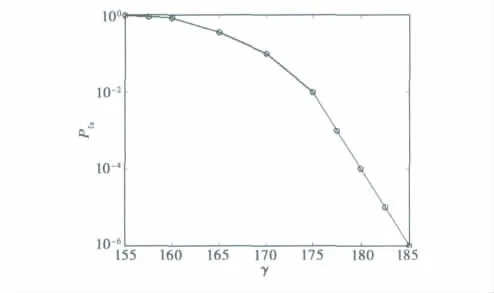
图2 虚警概率Pfa与检测门限γ关系曲线

图3给出了虚警概率Pfa＝10-4，积累帧数M＝30帧条件下，距离多普勒域中不同SNR时利用所提算法得到的某次目标航迹结果，其中图3（a）、（b）和（c）中接收回波数据的SNR分别为-5dB、-7dB和-12dB，由图可知，当SNR为-5dB时，所提算法得到的航迹与真实航迹吻合程度最好，当SNR为-7dB时，仍可明显检测出目标航迹，但当SNR为-12dB时已不能检测出目标航迹.

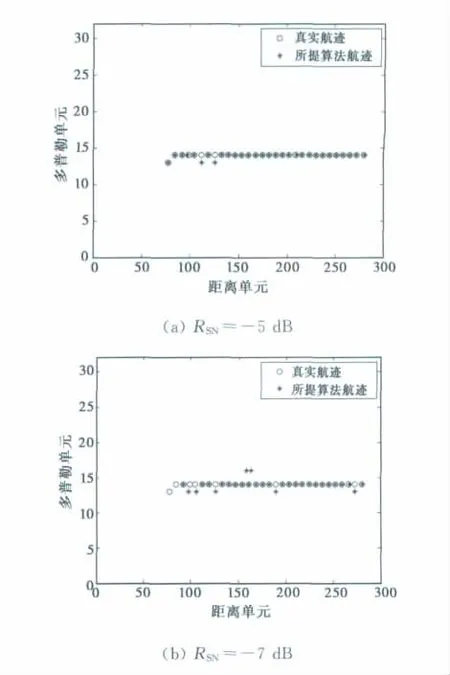
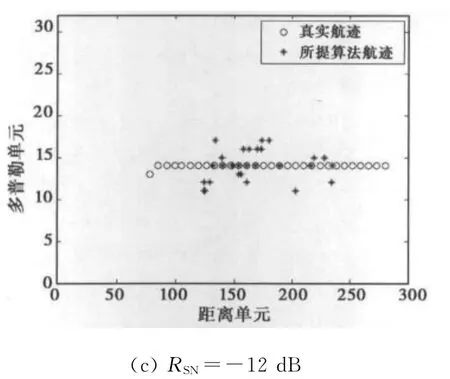
图3 距离多普勒域中不同SNR时的目标航迹

为了从统计意义上说明所提算法的有效性，下面通过Monte Carlo仿真实验计算目标航迹检测概率Pd与RSN间的关系，并与传统TBD算法［1］和文献［3］方法的检测性能进行比较，其中Monte Carlo仿真次数为104次.

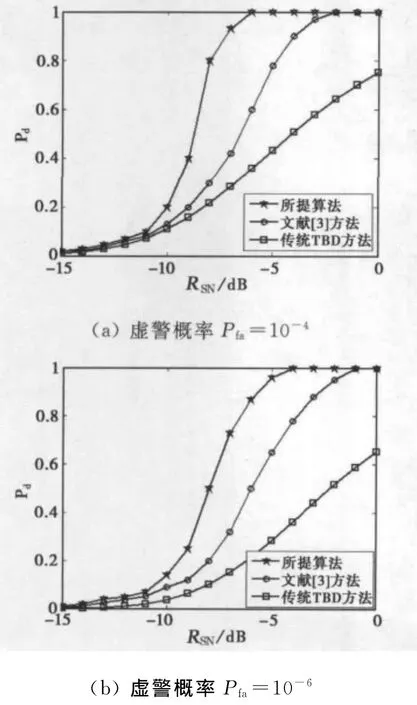
图4 不同虚警概率时的检测性能比较

图4（a）和（b）分别给出了虚警概率Pfa＝10-4（门限γ＝180）和Pfa＝10-6（门限γ＝185）条件下所提算法对应的检测性能曲线.作为比较，图中同时给出了相同虚警概率条件下传统TBD算法和文献［3］方法的检测性能曲线.由图可知，所提算法明显优于传统TBD算法和文献［3］方法，其中当检测概率Pd＝0.5时，与传统TBD算法相比，两种虚警概率情况下的SNR增益均有约5～6dB的改善；与文献［3］方法相比，两种虚警概率情况下的SNR增益均有约2～3dB的改善.

4 结 论

在低SNR背景中，雷达微弱目标完全被噪声淹没，传统的检测策略对微弱目标的检测性能欠佳.论文提出了一种距离多普勒域基于GLRT-DP的TBD算法.有效利用了雷达回波的帧内脉冲相参积累和多帧接收数据信息，以时间换取能量，大大提高了地面PD体制雷达对微弱目标的检测和航迹处理性能，仿真实验验证了该算法在低SNR背景中的有效性.

［1］TONISSEN S M，EVANS R J.Performance of dynamic programming techniques for track-before-detect［J］.IEEE Transactions on Aerospace and Electronic Systems，1996，32（4）：1440-1451.

［2］童慧思，张 颢，孟华东，等.PHD滤波器在多目标检测前跟踪中的应用［J］.电子学报，2011，39（9）：2046-2051.TONG Sihui，ZHANG Hao，MENG Huadong，et al.Probability hypothesis density filter multitarget trackbefore-detect application［J］.Acta Electronica Sinica，2011，39（9）：2046-2051.（in Chinese）

［3］罗小云，李 明，左 磊，等.基于动态规划的雷达微弱目标检测［J］.系统工程与电子技术，2011，33（7）：1491-1496.LUO Xiaoyun，LI Ming，ZUO Lei，et al.Radar weak target detection based on dynamic programming［J］.Systems Engineering and Electronics，2011，33（7）：1491-1496.（in Chinese）

［4］虞 欢，吴道庆，肖文书.距离-多普勒坐标系下基于相参积累的TBD算法研究［J］.中国电子科学研究院学报，2011，6（4）：386-390.YU Huan，WU Daoqing，XIAO Wenshu.Research on coherent integration based track-before-detect algorithm under range-Doppler reference frame［J］.Journal of CAEIT，2011，6（4）：386-390.（in Chinese）

［5］胡谋法，陈曾平.基于Zernike-Facet模型和总体最小二乘的弱小目标检测［J］.电子与信息学报，2008，30（1）：194-197.HU Moufa，CHEN Zengping.New small target detection algorithm via Zernike-Facet model and the total least squares［J］.Journal of Electronics ＆Information Technology，2008，30（1）：194-197.（in Chinese）

［6］陈 翼，王盛利.一种基于相参积累的检测前跟踪算法［J］.现代雷达.2010，32（5）：26-30.CHEN Yi，WANG Shengli.A track-before-detection algorithm based on coherent integration［J］.Modern Radar，2010，32（5）：26-30.（in Chinese）

［7］王 博，张建奇.一种空时域结合滤波的运动弱小目标检测方法［J］.西安电子科技大学学报（自然科学版）.2010，37（3）：524-528.WANG Bo，ZHANG Jianqi.Moving dim point target detection based on the spatial and temporal combined filter［J］.Journal of Xidian University，2010，37（3）：524-528.（in Chinese）

［8］REED I，GAGLIARDI R，STOTTS L.Optical moving target detection with 3-D matched filtering［J］.IEEE Transactions on Aerospace and Electronic Systems，1988，24（4）：327-336.

［9］REED I，GAGLIARDI R，STOTTS L.A recursive moving-target-indication algorithm for optical image sequences［J］.IEEE Transactions on Aerospace and E-lectronic Systems，1990，26（3）：434-440.

［10］鲜海滢，傅志中，李在铭.强噪声背景红外微弱动目标集成检测［J］.电波科学学报，2008，23（3）：438-442.XIAN Haiying，FU Zhizhong，LI Zaiming.Integration detection algorithm of infrared small dim moving target based on strong complex noise［J］.Chinese Journal of Radio Science，2008，23（3）：438-442.（in Chinese）

［11］KRAMER J，REID J.Track-before-detect processing for an airborne type radar［C］//Proceedings of the IEEE 1990International Radar Conference.Arlington，VA，1990：422-427.

［12］WALLACE W R.The use of track-before-detect in pulse-doppler radar［C］// Proceedings of the IEEE 2002International Radar Conference.Edinburgh，UK，2002：315-319.

［13］MORELANDE M，RISTIC B.Signal-to-noise ratio threshold effect in track before detect［J］.IET Radar Sonar Navi，2009，3（6）：601-608.

［14］ORLANDO D，RICCI G.Track-before-detect algorithms for targets with kinematic constraints［J］.IEEE Transactions on Aerospace and Electronic Systems，2011，47（3）：1837-1849.

［15］BUZZI S，LOPS M，VENTURINO L.Track-beforedetect procedures for early detection of moving target from airborne radars［J］.IEEE transactions on aerospace and electronic systems，2005，41（3）：937-954.

［16］BUZZI S，LOPS M，VENTURINO L，et al.Trackbefore-detect procedures in a multi-target environment［J］.IEEE transactions on aerospace and electronic systems，2008，44（3）：1135-1150.