基于高低频混合方法的梅利逼近扫频技术
马 骥 龚书喜 王 兴 张鹏飞 吕政良
(西安电子科技大学天线与微波技术国防科技重点实验室,陕西 西安710071)
引 言
随着现代电子技术的发展,宽频带系统的应用日益广泛.在实际应用中,宽带天线常常安装在舰船、飞机以及手机等移动平台上.为分析载体平台上天线在一定频率范围内的辐射特性,必须在每个频点重复求解积分方程,这必将耗费大量的时间.因此,如何快速有效得到载体平台上天线的宽带特性具有重要意义.
在电磁计算中,矩量法(MoM)[1]虽然是一种精确的数值方法,但受所需内存的限制,长期以来不能用于电大尺寸问题的求解.20世纪90年代以来,随着计算机硬件和计算方法的发展,计算电磁学取得了长足的进步.其中,MoM-PO[2-6]混合方法是研究此类问题的有效方法.该算法将整个模型划分为MoM区域和物理光学(PO)区域,由于MoM-PO方法中只有极少的未知量,因此具有比MoM高得多的计算效率,并且MoM区域的电场积分方程考虑了来自PO区域的耦合作用,使其计算精度得到保证.
基于模型估计[7]、渐近波形估计[8-9]和梅利逼近[10]等快速扫频技术蓬勃发展.上述方法中,梅利逼近易于与基于积分方程的数值方法相结合.本文将其与MoM-PO结合分析载体平台上天线的宽带特性,通过坐标变换,在给定的频带中计算出切比雪夫节点,并应用MoM-PO计算出这些节点处的表面电流,然后通过梅利逼近快速计算出该频带内任意频点的表面电流,从而实现宽带天线的快速扫频.计算结果表明在不失精度的前提下,该方法大大提高了计算效率.
1 基本理论
1.1 MoM-PO混合算法
考虑含有理想导体载体平台和天线的复杂结构,一般将天线划分为MoM区,而将载体平台划分为PO区.在MoM区应用导体目标边界条件可得电场积分方程为
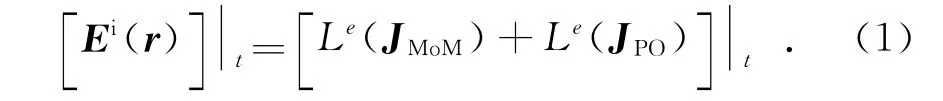
积分算子Le定义为
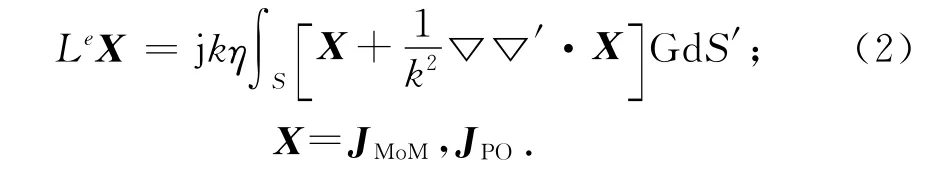
式中:k,η和G分别为自由空间的波数、波阻抗和格林函数;JMoM和JPO则分别代表MoM区和PO区的感应电流,将它们展开为

式中:NMoM和NPO分别为MoM区域和PO区域未知量数目;αn和γk分别是MoM区和PO区未知电流系数;fn和fk均为RWG基函数[11].
根据物理光学逼近,PO区的感应电流可表示为如下形式
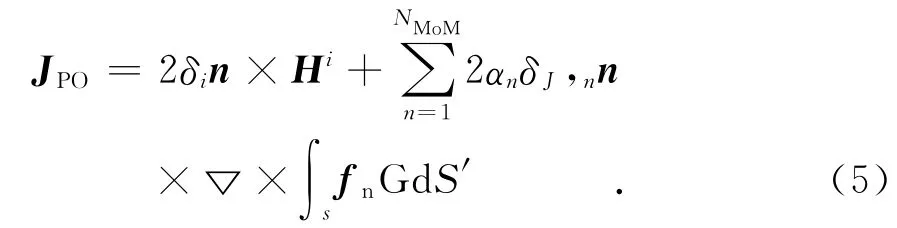
式中:n为PO区三角面片的单位法向矢量;δi和δJ,n分别代表了入射波(Ei,Hi)和MoM区基函数作为源对场点的遮挡系数,定义为
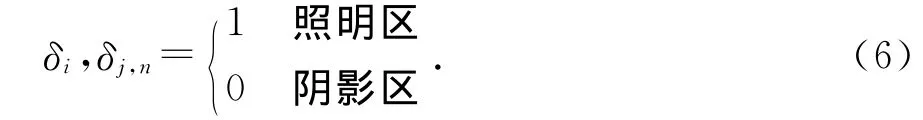
联立式(4)和或(5),并在PO区三角面片的公共边上引入一对垂直于该公共边的单位矢量tk±可得
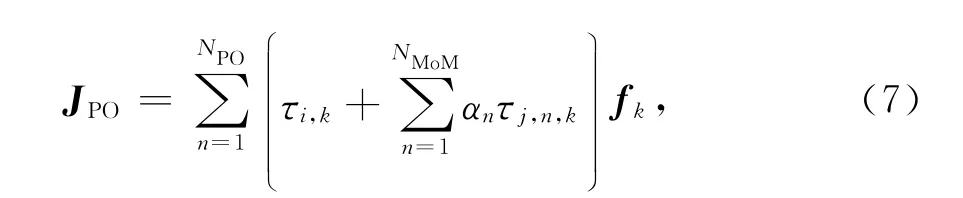
式中:
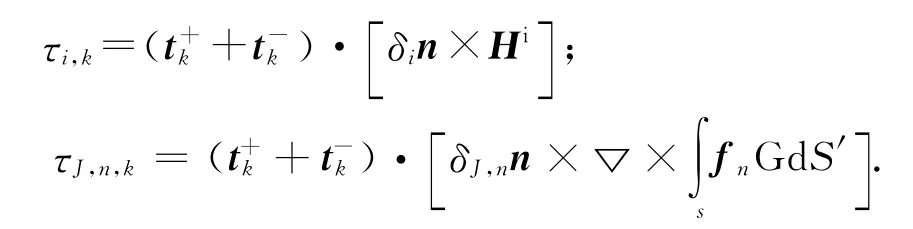
将式(3)和式(7)代入电场积分方程(1)中,并采用伽略金方法,利用测试函数fm(r)对方程(1)进行检验,可得如下矩阵方程
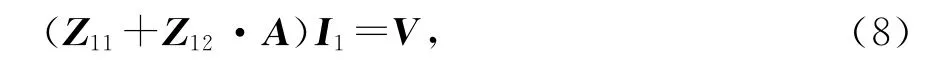
式中:Z11为MoM区的自阻抗矩阵;Z12和A分别为MoM区和PO区的互阻抗矩阵和耦合矩阵;I1为MoM区未知电流系数;V为激励向量.
PO区电流系数I2则可由下式得到

由此可以看出,相比于传统的MoM,MoM-PO将线性方程组的阶数由(NMoM+NPO)×(NMoM+NPO)降至NMoM×MMoM.一般情况下NMoM≪NPO,因此混合方法具有较高的计算效率.
1.2 梅利逼近
应用MoM-PO混合方法分析宽带电磁问题时可得如下矩阵方程

将MoM-PO与梅利逼近结合起来快速分析天线宽带特性,其具体步骤为:
1)对于给定频带f∈[fa,fb],对应波数为k∈[ka,kb],利用坐标变换得

2)设 Tl()(l=1,2,…,n)为l阶切比雪夫多项式,其定义如下
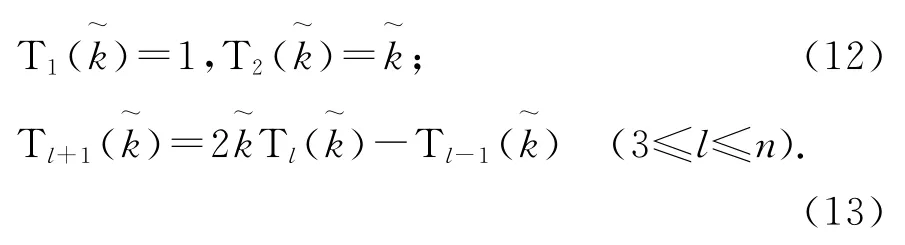
则n阶切比雪夫多项式Tn)的n个零点i为

由此,可在[ka,kb]中确定n个切比雪夫节点,其表达式为
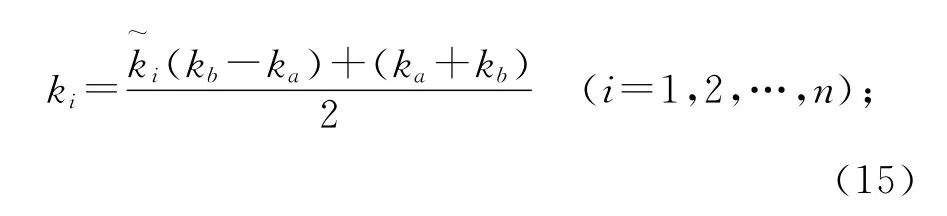
3)根据切比雪夫逼近,天线表面电流系数I1(k)可以表示为

式中

4)为提高计算精度,利用梅利有理展开逼近电流系数矢量,则I1(k)可重写如下
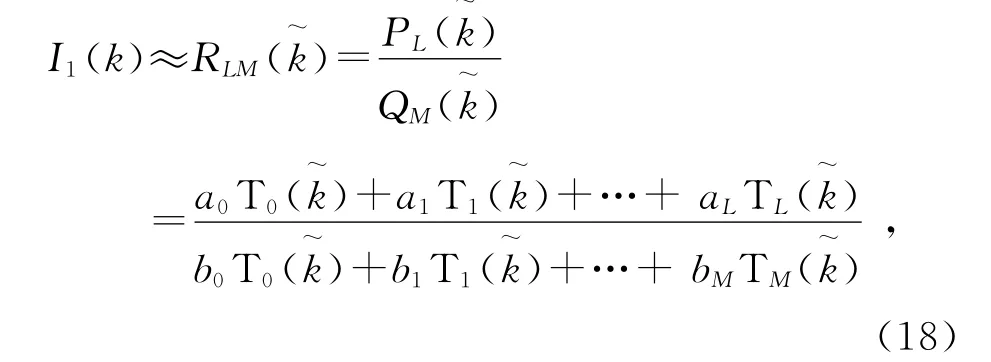
通常设b0=1,将式(18)代入式(16)并利用恒等式TP(x)· Tq(x)=(Tp+q(x)+T|p-q|(x))可得未知系数ai(i=0,1,…,L)和bj(j=1,2,…,M)如下:
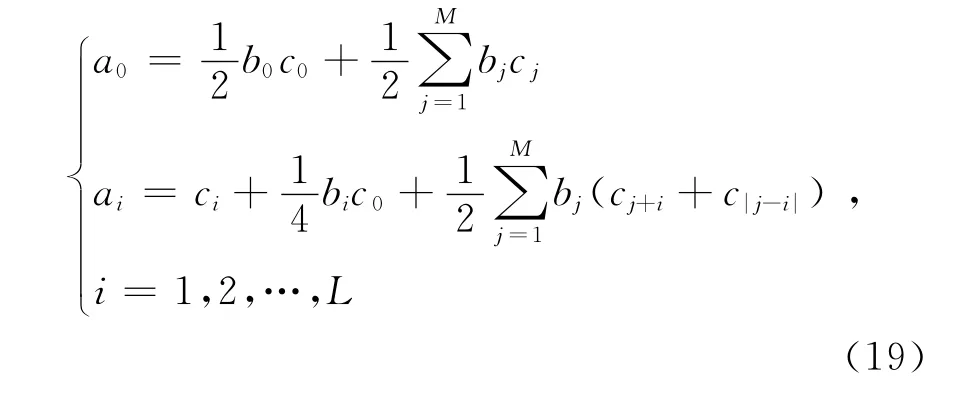
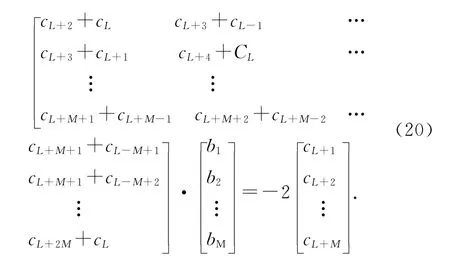
一旦有理函数系数ai和bj确定,将其代入式(18)即可求得给定频域内任意频点的电流密度,进而分析天线宽带特性.
2 算例分析

图1 导体板上方的对称振子天线
为验证算法的有效性,给出两个算例的数值结果.所有计算都在主频为2.8GHz的个人电脑上完成,迭代方法采用双共轭梯度法,数据采用双精度类型存储.
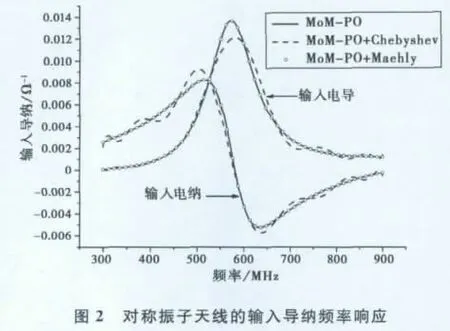
首先分析边长为2m的正方形理想导体平板上0.25m处水平放置的对称振子天线的宽带辐射特性.对称振子天线利用长为0.25m、宽为0.04m的细带建模,天线剖分为32个三角形,共31未知量,而平板剖分为2 048个三角形,共3 012未知量,如图1所示.利用MoM-PO方法进行计算时,天线选为MoM区域,平板为PO区域,计算频段为300~900MHz.图2给出了采用逐个频点计算、切比雪夫逼近(n=12)和梅利逼近(L=M=4)三种方法得到的对称振子天线输入导纳频率响应.可以看出:相比于切比雪夫逼近,梅利逼近与逐点计算的结果吻合更好,精度更高.将梅利逼近得到的天线工作在中心频率600MHz时电场辐射方向图(φ=0°,0°≤θ≤180°)与测试结果对比于图3.两条曲线吻合良好,由于该算法没有处理导体平板边缘绕射场,所以后瓣部分存在误差.
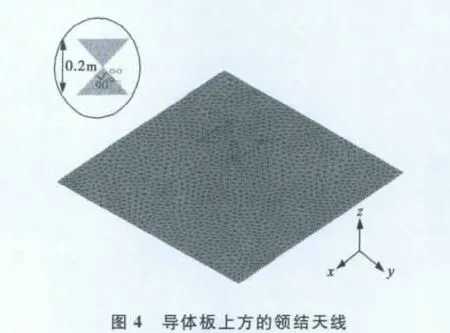
算例二考虑边长为1m的正方形导体板上0.24m处放置的领结天线.领结天线张角为90°,长0.2m,天线剖分为94个三角形,共117未知量,而平板剖分为2 420个三角形,共3 566未知量,如图4所示.天线为MoM区,平板为PO区,计算频段为0.6~1.9GHz.图5给出了领结天线的输入导纳频率响应曲线,图6则为应用梅利逼近方法得到的天线在xoz面辐射方向图随频率变化情况.从表1可以看出:由于MoM-PO混合算法减少了未知量个数,导致内存需求和计算时间比MoM有大幅度降低.如果进一步采用梅利逼近方法快速扫频,则可在160s内获取天线宽带特性.

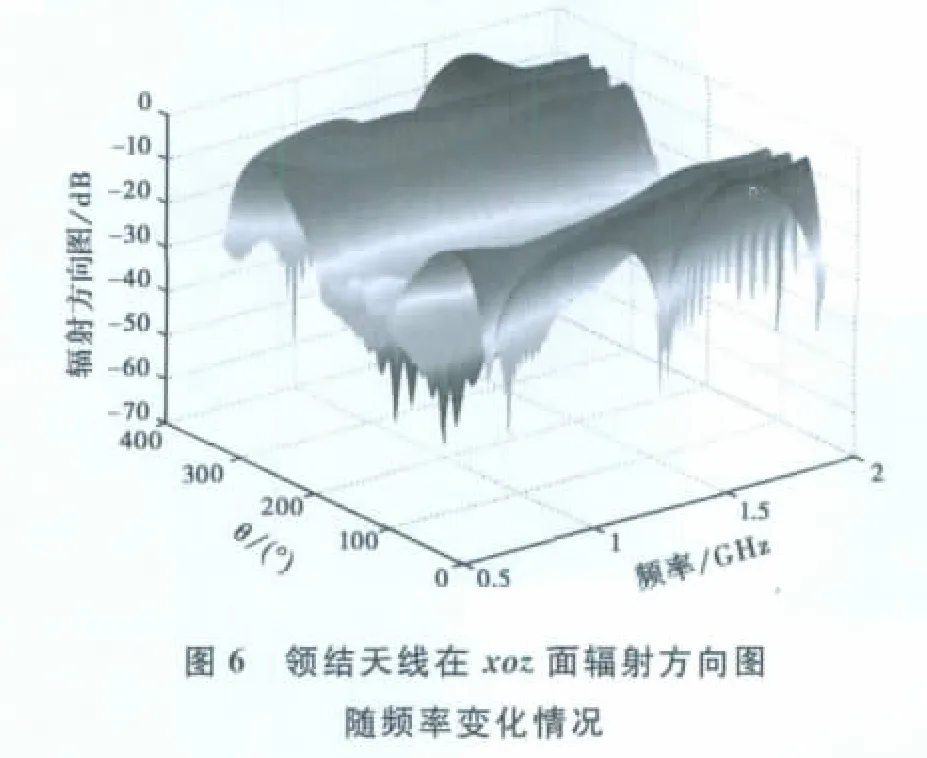
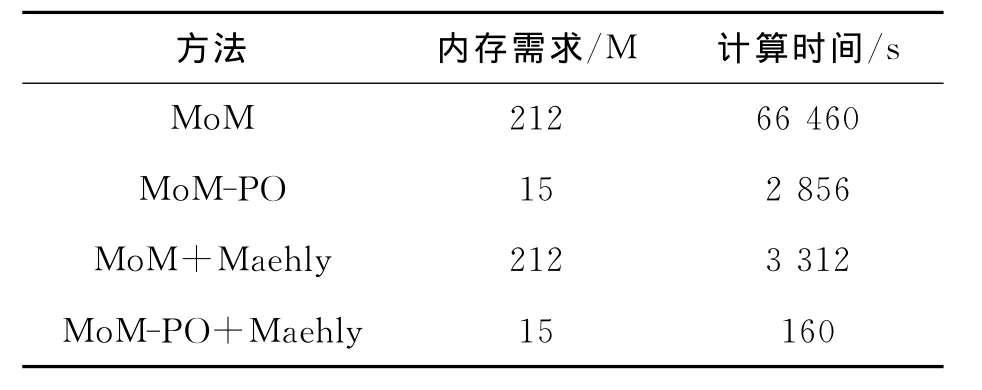
表1 算例二中不同方法内存需求与计算时间对比
3 结 论
在切比雪夫逼近的基础上,将梅利有理逼近引入MoM-PO混合方法中有效分析了载体平台上天线的宽带特性.数值结果表明:该方法的计算精度优于切比雪夫逼近,而相比于逐点计算,该方法大大降低了求解时间.因此,MoM-PO结合梅利逼近分析载体平台上天线特性对实际工程具有一定的指导意义.
[1]HARRINGTON R F.Field Computation by Moment Methods[M].New York:MacMillan,1968.
[2]JAKOBUS U,LANDSTORFER F M.Improved PO MM hybrid formulation for scattering from three-dimensional perfectly conducting bodies of arbitrary shape[J].IEEE Trans on AP,1995,43(2):162-169.
[3]JAKOBUS U,LANDSTORFER F M.Improvement of the PO-MM hybrid method by accounting for effects of perfectly conducting wedges[J].IEEE Trans on AP,1995,43(10):1123-1129.
[4]翟会清,王莉娜,梁昌洪.利用UTD修正的MoM-PO混合算法研究[J].电波科学学报,2003,18(5):529-533.ZHAI Huiqing,WANG Li'na,LIANG Changhong.A hybrid method of MoM and PO modified by UTD[J].Chinese Journal of Radio Science,2003,18(5):529-533.(in Chinese)
[5]陈海涛,罗建新,朱国强.基于UV/MoM-PO的电大载体附近阵列天线的研究[J].电波科学学报,2008,23(2):292-295.CHEN Haitao,LUO Jianxin,ZHU Guoqiang.Analysis of array located near to electric large-scale platform based on UV/Mom-PO method[J].Chinese Journal of Radio Science,2008,23(2):292-295.(in Chinese)
[6]陈亚萍,孙厚军,吕 昕.复合目标模拟器电磁仿真的研究[J].电波科学学报,2008,23(5):808-811.CHEN Yaping,SUN Houjun,LÜXin.Electromagnetic simulation of compound target simulator[J].Chinese Journal of Radio Science,2008,23(5):808-811.(in Chinese)
[7]BURKE G J,MILLER E K,CHAKRABARTHI S,et al.Using model-based parameter estimation to increase the efficiency of computing electromagnetic transfer functions[J].IEEE Trans on Mag,1989,25(7):2807-2809.
[8]REDDY C J,DESHPANDE M D,COCKRELL C R,et al.Fast RCS computation over a frequency band using method of moments in conjunction with asymptotic waveform evaluation technique[J].IEEE Trans on AP,1998,46(8):1229-1233.
[9]WANG Xing,GONG Shuxi,GUO Jingli,et al.Fast and accurate wide-band analysis of antennas mounted on conducting platform using AIM and asymptotic waveform evaluation technique[J].IEEE Trans on AP,2011,59(12):4624-4633.
[10]CHEN M S,WU X L,SHA W,et al.Fast and accurate radar cross-section computation over a broad frequency band using the best uniform rational approximation[J].IET MAP,2008,2(2):200-204.
[11]RAO S M,WILTON D R,GLISSON A W.Electromagnetic scattering by surfaces of arbitrary shape[J].IEEE Trans on AP,1982,30(3):409-418.

