球形破片侵彻明胶的瞬时空腔模型

莫根林，吴志林，刘坤

(南京理工大学 机械工程学院，江苏 南京210094)

0 引言

创伤弹道实验中常采用明胶作为人体肌肉组织的替代物。弹头侵彻明胶过程中通过3 种方式将能量传递给周围的明胶:切割作用、压力波和瞬时空腔。实验表明瞬时空腔使得弹道周围的明胶拉伸破坏，瞬时空腔被认为是创伤效应中最大的影响因素[1－2]。因此，研究投射物穿透明胶过程中瞬时空腔的形成规律对于阐明投射物的致伤机制具有十分重要的意义。

钱有林[3]对空腔效应的形成机理及其影响因素进行了探讨，并运用模糊数学的观点预估空腔的大小。Fackler 等[4]沿弹道方向将明胶块分割成很多明胶切片，将明胶切片中最长的两道裂纹长度之和作为该处最大的瞬时空腔直径;结合明胶切片到明胶块表面的距离，利用最大空腔直径的包络线描述弹头的致伤效应(WP)方法。裂纹总长测量(TCL)方法以明胶切片中所有裂纹长度之和作为该处瞬时空腔的最大周长[5]。多边形测量(PP)方法将明胶切片中裂纹形成的多边形周长作为瞬时空腔的最大周长[6]。这些方法是以测量静态裂纹长度作为致伤效应评估的基础，而明胶中的裂纹有时候很难辨识。采用高速摄影获得的空腔数据表明上述方法带来的误差可以达到50%[7].Schyma[6]通过在明胶块前放置染料，光学扫描明胶切片的方法提高了裂纹的辨识度。对弹头侵彻明胶实验数据的分析表明明胶中裂纹的产生和明胶吸收的能量成线性关系[8]。文献[9]建立的最大瞬时空腔(MTC)模型将瞬时空腔最大值和弹头的运动速度、直径、迎风面积等因素联系起来。该模型无需借助实验即可获得瞬时空腔的最大值。上述模型没有建立瞬时空腔随时间的变化关系。Liu 等[10]假设明胶为不可压缩材料，将空腔膨胀的能量分为弹性能和塑性能，建立了空腔的运动模型。

1 实验材料与方法

采用质量百分比10% 的弹道明胶，密度为1 030 kg/m3，尺寸为30 cm×30 cm ×30 cm.实验前将明胶块放在4 ℃的冰箱中保温24 h.实验中采用弹道枪作为发射装置，弹道枪距离明胶块25 m.光电靶放置在明胶块前1 m 处，高速摄影机放置在明胶块侧面与明胶块等高，实验装置如图1 所示。实验装置固定后，在明胶块位置放置刻度尺并用高速拍摄其图像，为空腔实验数据的读取做准备。采用直径为3 mm、4 mm 和4.8 mm 的钢球作为侵彻破片，钢球的速度范围为650 ～1 000 m/s.实验时将明胶块放置在光线充足的场所，破片垂直侵彻明胶块，采用高速摄影机Phantom v120 拍摄钢球在明胶块中的运动和瞬时空腔的运动。高速摄影的拍摄频率为10 000 f/s，曝光时间5 μs，图像分辨率为1 024 像素×512 像素，拍摄时长2 s.

图1 实验装置示意图Fig.1 Schematic diagram of experimental apparatus

2 实验结果和分析

2.1 数据的读取

图2 为4 mm 钢球侵彻明胶过程中的瞬时空腔。从图中可以看出，空腔和明胶有明显的分界线，利用带有刻度尺的图像和Phantom Camera Control 软件的Measure 功能即可标定图像中空腔的尺寸。将坐标系设定在选定的截面位置，通过读取空腔分界线的纵坐标，得到空腔位移随时间的变化关系。图3 ～图6 显示直径为3 mm、4 mm、4.8 mm、4.8 mm 钢球分别以660 m/s、720 m/s、727 m/s 和938 m/s 速度侵彻明胶时，不同截面处空腔位移随时间的变化曲线。

图2 4 mm 钢球侵入明胶时的瞬时空腔Fig.2 Temporary cavity for 4 mm steel sphere penetrating into gelatin block

2.2 空腔运动模型

假设明胶为弹性介质，其变形为平面轴对称变形。令明胶的空腔半径为u0，假设截面半径r 处明胶的径向位移

根据弹性胡克定律，明胶的运动方程表示为

式中:ρ0、λ 和G 分别为明胶的密度、拉梅常数和剪切模量。(2)式对半径r 从0 ～R 进行积分，得

图3 3 mm 钢球以速度660 m/s 侵彻时空腔实验数据Fig.3 Movement of cavity wall for 3 mm steel sphere penetrating into gelatin at 660 m/s

图4 4 mm 钢球以速度720 m/s 侵彻时空腔实验数据Fig.4 Movement of cavity wall for 4 mm steel sphere penetrating into gelatin at 720 m/s

图5 4.8 mm 钢球以速度727 m/s 侵彻时空腔实验数据Fig.5 Movement of cavity wall for 4.8 mm steel sphere penetrating into gelatin at 727 m/s

求解(3)式并利用初始条件t=0，u0=0 得

图6 4.8 mm 钢球以速度938 m/s 侵彻时空腔实验数据Fig.6 Movement of cavity wall for 4.8 mm steel sphere penetrating into gelatin at 938 m/s

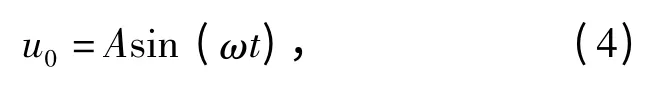
式中:A 为瞬时空腔最大幅值;ω 为空腔振动角频率。

假设空腔内壁的运动规律仅和该截面获得的能量有关，(4)式表示为

（2）结晶法：取少量样品，分别滴几滴水，振荡试管，结块并放热的是N a2CO3（N a2CO3粉末遇水生成含有结晶水的碳酸钠晶体——水合碳酸钠N a2CO3·xH2O）。

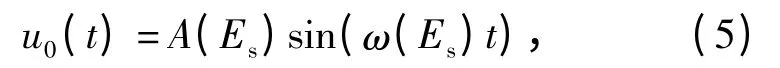
式中:Es为截面获得的能量(J/m)，A 和ω 为Es的函数。

2.3 Es的求解

文献[11 －12]建立了球形破片侵彻明胶的运动方程，其基本形式为

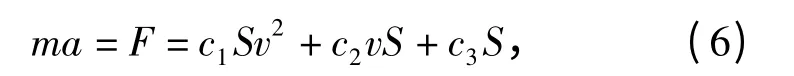
式中:m、a、v、F 和S 分别为球形破片的质量、加速度、速度、受力和迎风面积。通过对钢球位移时间曲线的拟合，取c1= － 360 kg/m3，c2= 0，c3=－680 000 N/m2.对(6)式进行求解，得到速度－位移的表达式为

式中:v0为破片的初始速度;x 为侵彻深度。假设截面获得的能量等于球形破片在该处损失的能量即，

式中:E 为球形破片的总动能。将(6)式和(7)式带入(8)式求得弹道方向任意位置的Es.

2.4 参数拟合

实验中观察到空腔入口处明胶有一定程度的轴向运动，为使实验数据符合平面运动假设，对侵彻深度大于4 cm 的空腔实验数据进行正弦函数拟合。将3 mm、4 mm 和4.8 mm 钢球实验拟合的幅值、角频率，以及Es汇总起来，再通过最小二乘法拟合得到幅值A 和Es的关系如图7 所示，表达式为

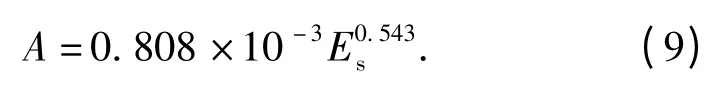
角频率ω 和Es的关系如图8 所示，其表达式为

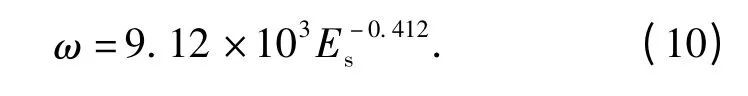
图7 空腔幅值和能量的关系Fig.7 A v.s.Es

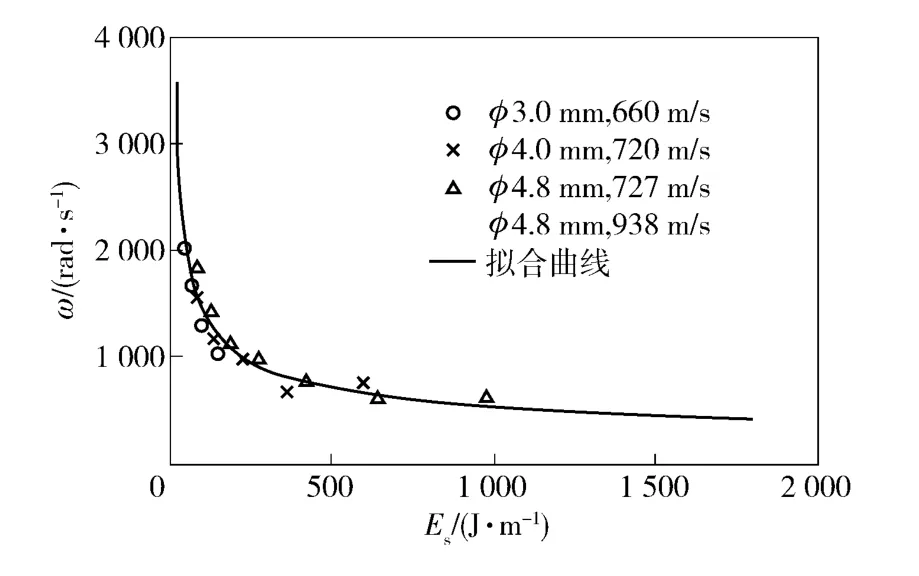
图8 空腔角频率和能量的关系Fig.8 ω v.s.Es

3 实验验证

用直径5.2 mm 钨球以800 m/s 速度侵彻明胶的实验验证上述模型。图9 为6 个截面位置的空腔位移数据。对实验数据进行正弦函数的拟合，空腔幅值和角频率的模型预测值和实验拟合值的比较分别如图10 和图11 所示。空腔幅值的相关系数为0.95;空腔角频率的相关系数为0.23，除去40 mm处角频率数据，其相关系数为0.75.从比较结果可以看出，该模型能较好地预测空腔最大幅值和空腔振动角频率，模型对空腔入口处振动角频率的预测误差较大。

4 结论

图9 5.2 mm 钨球以800 m/s 速度侵彻明胶的空腔实验数据Fig.9 Movement of cavity wall for 5.2 mm tungsten sphere penetrating into gelatin at 800 m/s

图10 空腔幅值预测值和实验值比较(钨球直径为5.2 mm、侵彻速度为800 m/s)Fig.10 Comparison of cavity amplitude A (5.2 mm tungsten sphere，800 m/s)

图11 角频率预测值和实验值比较(钨球直径为5.2 mm、侵彻速度为800 m/s)Fig.11 Comparison of frequency ω (5.2 mm tungsten sphere，800 m/s)

本文研究了球形破片侵彻明胶时瞬时空腔随时间的变化过程。采用正弦函数描述空腔内壁运动的规律，通过数值拟合得到了空腔振动幅值和能量、角频率和能量的经验公式。该模型可以有效地预测不同直径、不同材质球形破片作用下的瞬时空腔大小和振动周期。

References)

[1]Bartlet C S.Clinical update:gunshot wound ballistics[J].Clinical Orthopaedics and Related Research，2003，408:28 －57.

[2]Griffiths D，Clasper J.(iii)Military limb injuries/ballistic fractures[J].Current Orthopaedics，2006，20(5):346 －353.

[3]钱有林.空腔效应初探[J].兵工学报:弹箭分册，1988，(2):23 －31.QIAN You－lin.Exploration of cavity effect[J].Acta Armamentarii:Projectiles and Rockets，1988，(2):23 －31.(in Chinese)

[4]Fackler M L，Bellamy R F，Malinowski J A.The wound profile:illustration of the missile－tissue interaction[J].The Journal of Trauma and Acute Care Surgery，1988，28(1):S21 － S29.

[5]Ragsdale B D，Josselson A.Predicting temporary cavity size from radial fissure measurements in ordnance gelatin[J].The Journal of Trauma and Acute Care Surgery，1988，28(S1):S5 －S9.

[6]Schyma C W A.Colour contrast in ballistic gelatine[J].Forensic Science International，2010，197(1):114 －118.

[7]Zhang J，Yoganandan N，Pintar F A，et al.Temporal cavity and pressure distribution in a brain simulant following ballistic penetration[J].Journal of Neurotrauma.2005，22(11):1335 －1347.

[8]Schyma C，Madea B.Evaluation of the temporary cavity in ordnance gelatine[J].Forensic Science International，2012，214(1):82 －87.

[9]Peters C E，Sebourn C L.Wound ballistics of unstable projectiles.Part II temporary cavity formation and tissue damage[J].The Journal of Trauma and Acute Care Surgery，1996，40(3S):16S－21S.

[10]Liu L，Fan Y，Li W，et al.Cavity dynamics and drag force of high－speed penetration of rigid spheres into 10wt% gelatin[J].International Journal of Impact Engineering，2012，50:68 －75.

[11]Seletes S B.Modeling the penetration behavior of rigid spheres into ballistic gelatin，ADA479045[R].Alexandria:DTIC，2008.

[12]刘坤，吴志林，徐万和，等.球形破片侵彻明胶修正力学模型[J].南京理工大学学报，2012，36(5):1 －7.LIU Kun，WU Zhi－lin，XU Wan－he，et al.Correction mechanical model of spherical fragments penetrating gelatin[J].Journal of Nanjing University of Science and Technology，2012，36(5):1－7.(in Chinese)