基于分数阶神经滑模的某顶置火炮调炮控制

高强，侯润民，杨国来，毛斌，侯远龙

(1.南京理工大学 机械工程学院，江苏 南京210094;2.北方重工业集团 科研所，内蒙古 包头014033)

0 引言

某顶置火炮炮控系统采用交流电机驱动伺服系统，该系统存在诸多非线性环节，如不同工况及外部环境变化引起系统参数的时变、行进过程中路面颠簸造成的随机负载扰动、高低向的不平衡力矩和发射时的冲击力矩等力矩扰动，以及炮身与火炮耳轴之间的复杂非线性摩擦特性等[1－2]。严重制约了火炮射速、稳定跟踪精度等性能指标的提高。PID 控制器作为一种简单而实用的控制方法，在实际炮控系统中获得了广泛的应用。然而，实际炮控伺服系统中不可避免的诸多非线性环节使得PID 控制下的调炮操作难以获得理想的动、静态品质。

滑模控制(SMC)作为变结构控制的一种，具有对参数变化及外部扰动不敏感、无需被控系统精确数学模型等优点，已成为非线性控制领域关注的热点问题之一[2]。为了进一步提高系统的容错性，并削弱SMC 固有之“抖振”现象，基于模糊推理(FR)、人工神经网络(ANN)等自适应策略被融入到SMC，获得了较好效果[2－5]。然而该类自适应SMC 为了获取强鲁棒性与平稳性，牺牲了系统的稳态跟踪精度与响应时间。

分数阶微积分(FOC)将传统的微积分阶次拓宽到任意数，具有无限维度、遗忘性记忆等特性，已有的研究结果证明:分数阶控制系统对外部扰动不敏感，对非线性系统具有极好的控制性能[6－8]。基于此，Calderon 等[9]提出了分数阶滑模控制器用于电子降压转换器的控制;文献[10 －11]针对多输入多输出非线性动力学系统的控制问题，分别设计了一种分数阶滑模面及一种自适应分数阶切换函数，以提高系统的运动控制性能。前人的研究成果表明:FC 的引入使得传统滑模控制策略在获得良好跟踪精度的同时，保持了很好的鲁棒性及响应特性，并能削弱系统的抖振现象，展现了应用前景[9－11]。然而，目前国内外学术界对分数阶型SMC (FSMC)的研究较少，且以理论研究为主，缺乏实际应用实例的支持[10－13]。

结合ANN 容错性强，及FSMC 的固有优点，本文设计了一种基于分数阶PID 滑模面的FSMC，进一步引入RBF 神经网络，提出了一种分数阶神经网络滑模控制(FNSMC)策略，将其应用于顶置火炮的调炮控制。通过数值仿真及半实物仿真试验，系统的研究了该FNSMC 的控制性能及特征，验证了该控制策略优良的控制效果。

1 某顶置火炮炮控系统

某顶置火炮高低向炮控采用交流电机伺服控制系统，其系统框图如图1 所示。

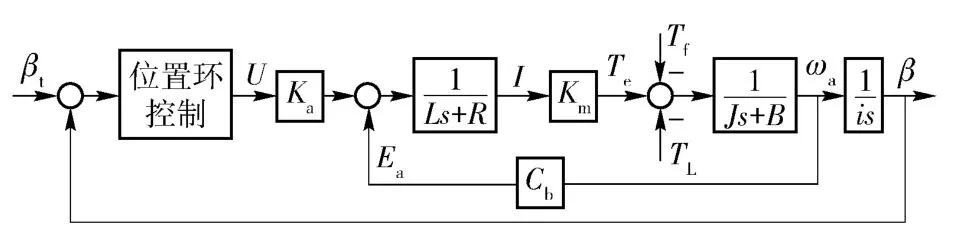
图1 炮控交流伺服系统结构图Fig.1 Diagram of gun control AC servo system

图1中:βt为目标位置;β 为火炮高低角;U 为控制电压;Ka为放大器增益;R 为电机电枢回路电阻;L 为电机电枢回路电感;Km为电机力矩系数;Te为电机电磁转矩;Ea为电机电枢反电动势;Cb为电机反电动势系数;TL为负载扰动力矩;Tf为摩擦力矩扰动;J 为折算到电机转子上的总转动惯量;B 为粘性摩擦系数;ωa为电机角速度;i 为减速比。

在实际工作过程中，系统的转动惯量J、粘性摩擦系数B、负载扰动力矩TL及摩擦力矩扰动Tf等各参量具有明显的不确定性，且随着工况的变化而产生状态漂移，表现出强烈的非线性时变动态特征。

工作过程中，电机中电流时间常数远小于机械时间常数，电流响应的延迟时间可以忽略，即

式中:s 为拉普拉斯算子。

电机电磁转矩为

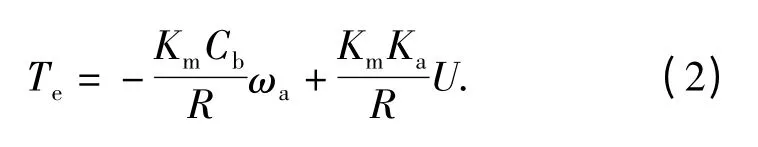
由转矩平衡方程可得

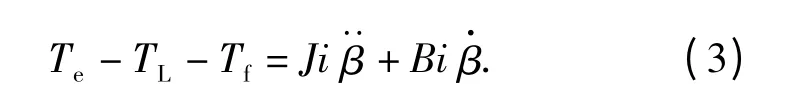
将(2)式代入(3)式可得

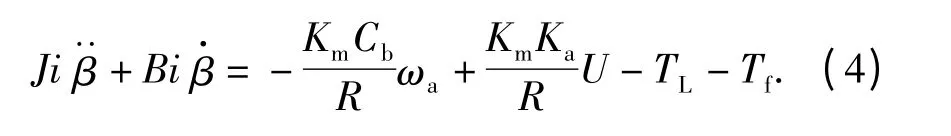
(4)式两边同乘以1/i，并整理得

取状态变量为X=[x1x2]T，令x1=β，x2=则系统状态空间方程为

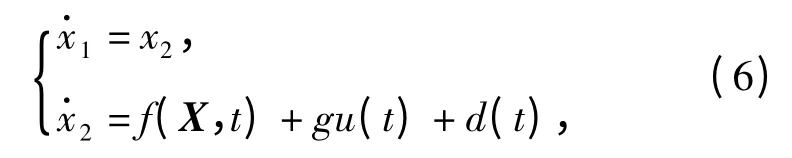
在工作过程中，将理想状态变量定义为

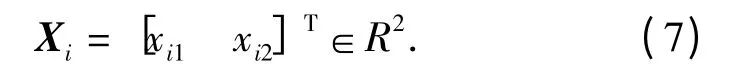
跟踪误差e(t)∈R2定义为

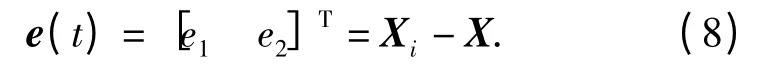
炮控交流伺服系统的非线性动力学方程f(X，t)难以精确获得，对其进行线性化假设，利用系统辨识方法可获得其近似线性化方程以下f(X，t)即指，并满足:

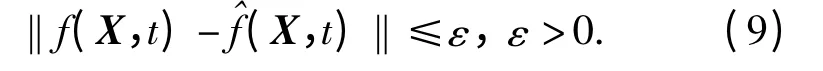
炮控伺服系统的控制目标即为使实际状态X(t)时刻跟踪给定的理想状态Xi(t)，以保证跟踪误差e(t)趋近于0.

2 分数阶神经滑模控制器

2.1 分数阶微积分

FOC 和传统的整数阶次微积分几乎同时被提出，已有300 余年的历史，由于计算水平的限制，FC一直停留在理论探讨上。随着计算机技术的高速发展，FC 已被逐步引入到工程技术、自然科学、社会科学等各个领域，受到了国内外学者的广泛关注。

令t0表示FC 算子，t 和t0分别为微积分的上下界，α 为FC 算子的阶次，D 表示分数阶操作算子。连续的FC 算子定义[6－9]为

式中:Re (α)为阶数α 的实部。

FC 算子的实现主要有Grunwald－Letnikov (G－L)定义和Riemann－Liouville (R－L)定义。根据G－L 定义)可写为

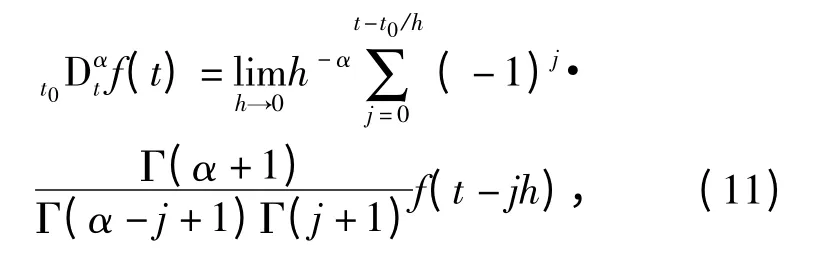
式中:h 为计算步长;Γ(·)为欧拉Gamma 函数。根据R－L 定义，t0)可写为

RL 定义下分数微积分的Laplace 变换为

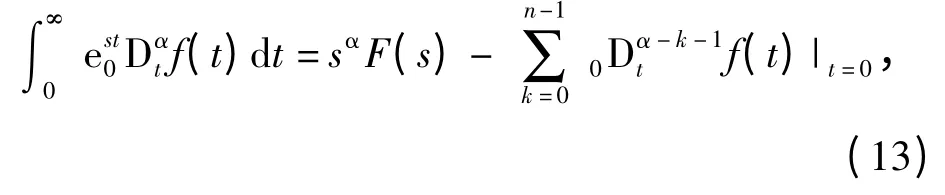
式中:k 为整数。

在0 初值条件下，FC 的Laplace 变换(R－L 定义和G－L 定义)均可写为

2.2 分数阶神经滑模控制器设计

SMC 的设计过程主要分为2 步:1)选择合适的滑模面S=0，以保证滑模运动满足设计要求;2)选择合适的切换函数，以保证状态轨迹能收敛于滑模面。

2.2.1 分数阶PID 滑模面设计

典型的PID 型滑模面[14]为

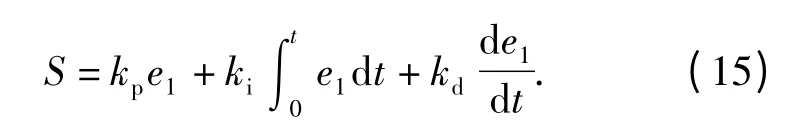
引入FC，设计分数阶PID 滑模面为

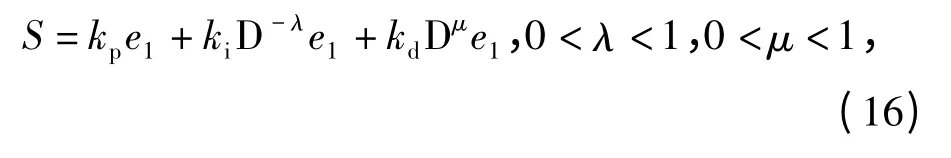
式中:kp，ki和kd分别为比例、积分和微分增益;λ 和μ 分别为积分和微分阶次;e1为误差。对(16)式两端进行微分操作，可得

结合误差定义(7)式与(8)式，(17)式可改写为

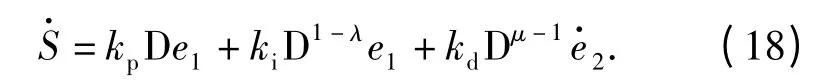
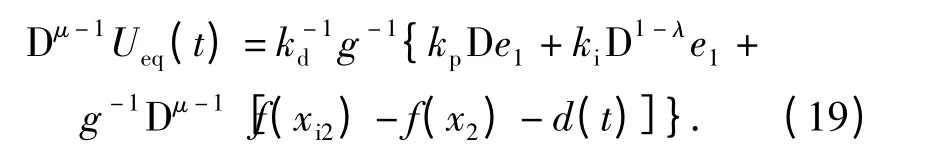
由(19)式可解得等效控制量为

当系统进入滑模态时，整数阶系统以指数e－t形式收敛到平衡态，而分数阶系统则以t－r形式收敛于平衡态，r 依赖于分数阶系统的阶次[15－16]。分数阶滑模这种特有的收敛态可使控制系统更为缓慢地传递能量，这将极大程度上削弱系统抖震，提高系统跟踪精度[15－16]。通过设置分数阶的阶次，可以主动调节控制系统的收敛模式及动态特征，以获得更优的动静态品质。同时，由分数阶算子G－L 定义可知，分数阶操作算子具有非局部性，即其对历史状态具有遗忘记忆性，这将降低分数阶控制系统对外部扰动的敏感性，增强控制系统的鲁棒性。

2.2.2 基于RBF 神经网络的切换函数设计

等效控制Ueq是为了使系统状态参量处于滑模面S=0 内，若超出了滑模面，应合理选择切换函数，以使系统状态参量渐趋进入滑模面。为满足趋近条件

滑模控制中较常使用的切换函数为

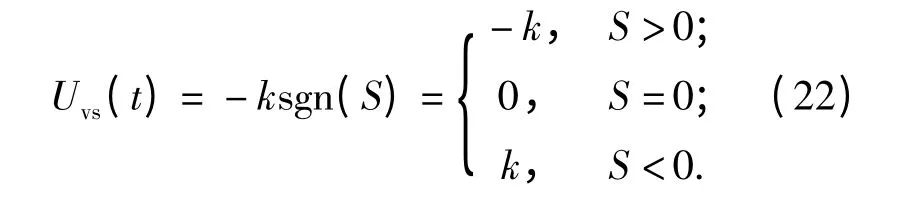
式中:sgn(·)为符号函数;k 为切换增益。在使用(22)式时，由于符号函数的非连续性，状态参量在接近滑模面时，将产生“抖振”现象。本文采用饱和函数sat(·)代替符号函数sgn (·)以平滑控制信号，减弱抖振现象。因此，改进后的切换函数为

由于外部扰动及系统参数具有时变性，固定的切换增益难以获得最优的控制性能。本文提出了一种基于RBF 神经网络的切换增益动态调节方法，以在尽可能小的抖振条件下，获得尽可能高的跟踪精度和尽可能短的响应时间。用于RBF 神经网络权值调整的多目标最小化指标定义为

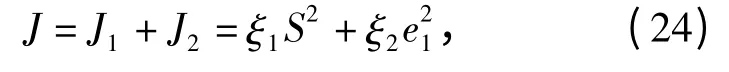
式中:ξ1和ξ2为权重。

RBP 网络权值增量及学习算法[17]分别为

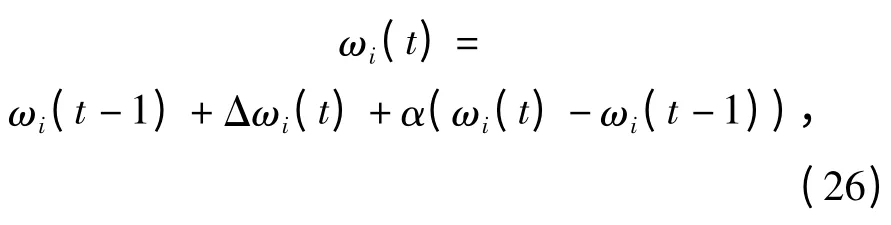
式中:ωi为RBF 神经网络中第i(i =1，2，…，n)个隐节点到输出节点的连接权值;η 为学习率;α 为动量因子。

RBF 神经网络输出的切换增益为

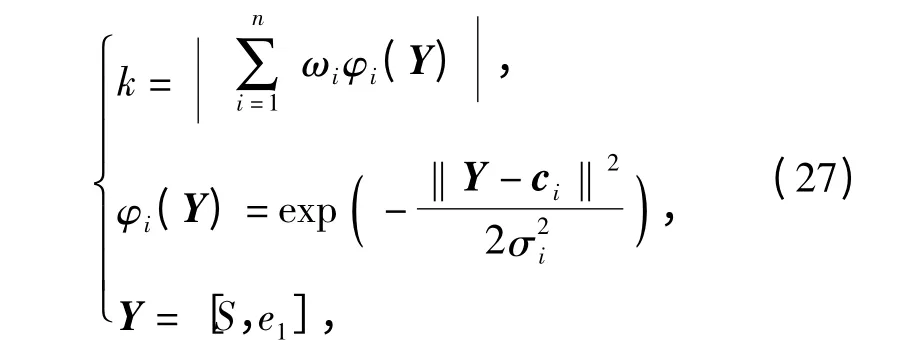
式中:n 为隐含层节点个数;ci=[ci1，ci2]T为第i 个隐节点径向基函数的中心;‖Y－ci‖为输入Y 与中心ci的欧几里得范数;σi为第l 个隐节点径向基函数的宽度。

由此可得，本文所提出的FNSMC 输出控制量为

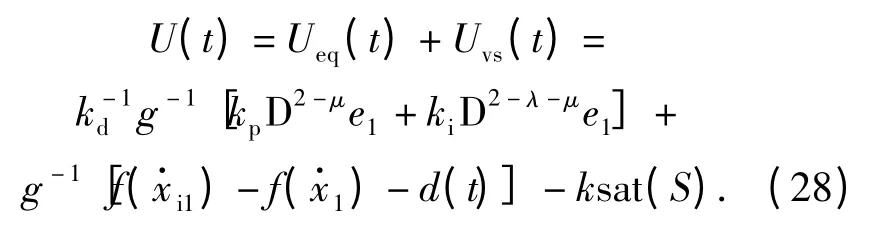
由(28)式可知，令λ =μ =1，即为文献[14]所提出的传统整数阶神经网络滑模控制(CNSMC).

3 FSMC 性能比较与讨论

为比较所设计FSMC 性能的优越性，本文基于该交流伺服系统，采用数值仿真方法比较了相同条件下FSMC 与传统基于整数阶滑模面的SMC(CSMC)控制系统阶跃相应特性。两种控制系统下系统阶跃响应如图2(a)所示，相应的控制电压如图2(b)所示。滑模面收敛轨迹相图如图3(a)所示，其局部特征放大如图3(b)所示。

由图2(a)可知，尽管FSMC 与CSMC 均能获得零稳态定位误差，但CSMC 的响应时间约0.8 s，而FSMC 的响应时间约0.35 s，较之CSMC 约减少了1 倍。这表明FSMC 控制系统具有更快的响应速度。由图2(b)中相应的控制电压可以看出，FSMC 控制电压的颤振电压PV 幅值约为0.25 V，约为CSMC的40%，这表明:较之CSMC，FSMC 能够有效地抑制削弱抖振现象。由图3 可知，FSMC 仅在非常接近平衡态时发生颤振现象，且幅值远小于CSMC，能够更为平滑地趋近稳态，具有明显优于CSMC 的动态品质。

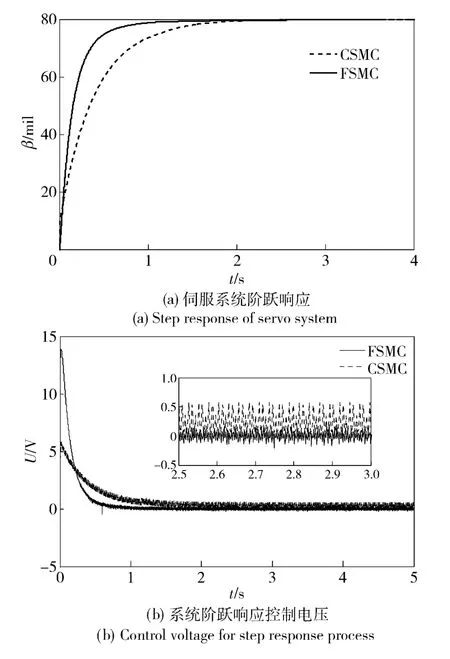
图2 伺服系统阶跃响应特征Fig.2 Step response process of servo system

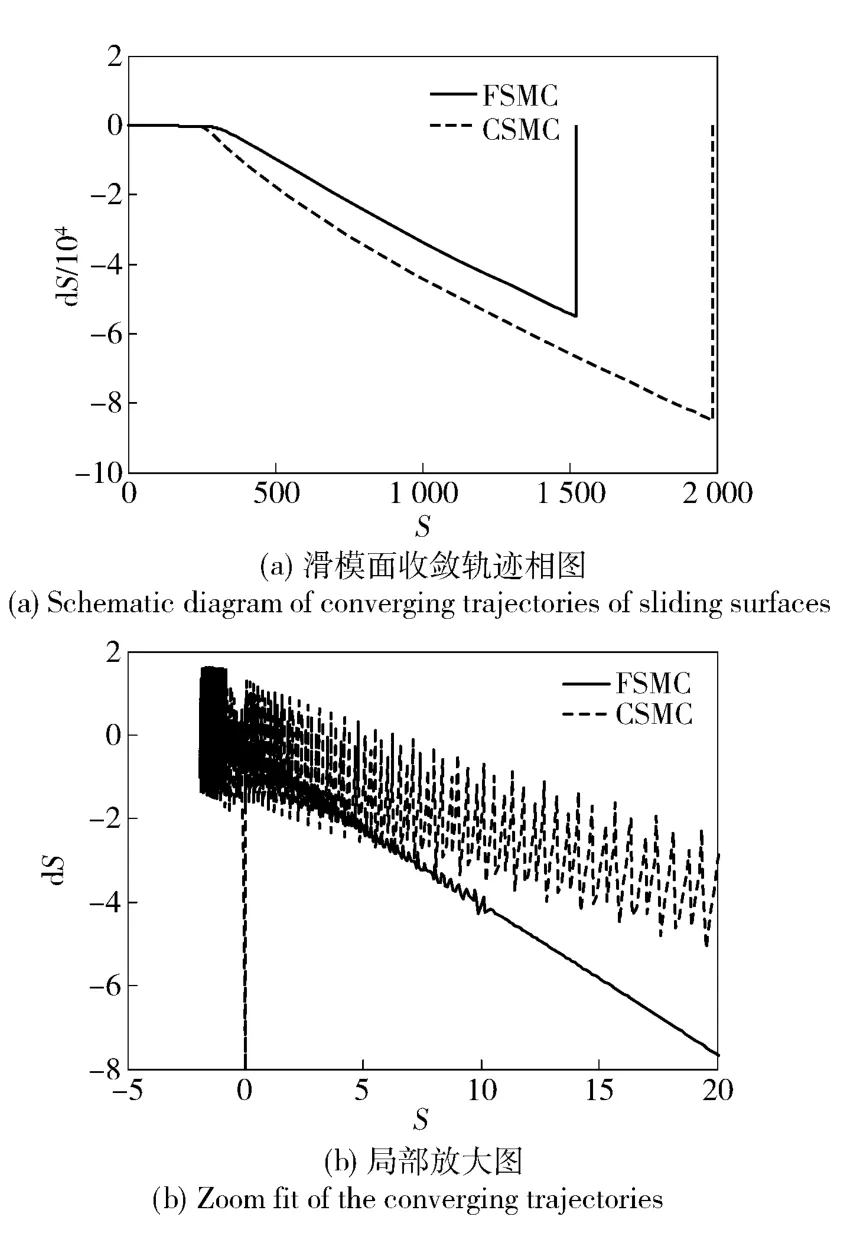
图3 滑模面收敛轨迹Fig.3 Converging trajectories of sliding surfaces

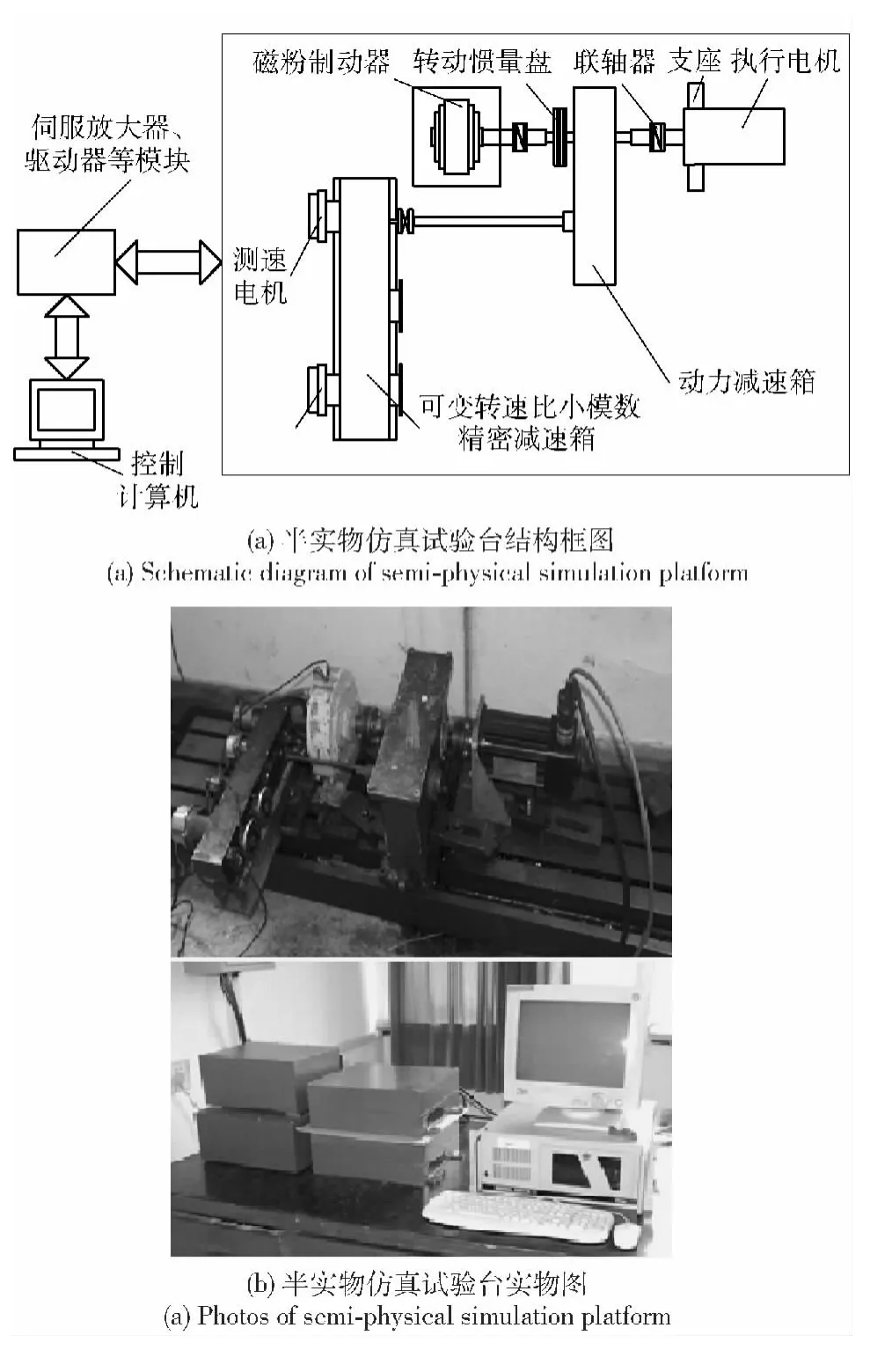
图4 半实物仿真试验台Fig.4 Semi－physical simulation platform

4 半实物台架试验

为验证本文所提FNSMC 策略的可行性及优异性，搭建了该伺服系统的半实物仿真试验平台，并在该平台上进行了阶跃响应及谐波跟踪试验测试，并与CNSMC 控制系统试验结果进行了比较，以验证本文所提FNSMC 性能的优越性。

该半实物仿真试验台结构框图及实物图分别如图4(a)及图4(b)所示，主要由控制计算机、测量系统(旋转变压器、RDC 模块等)、伺服放大器、减速箱、加载装置、执行电机及试验台架等组成。加载装置包括转动惯量盘及磁粉制动器，主要用来模拟该炮控系统在实际工况下的转动惯量及摩擦阻力矩。通过改变转动惯量盘可以模拟加载转动惯量的变化，控制磁粉制动器的输出扭矩，可以模拟系统的各种摩擦阻力矩。

图5 给出在Tf=6 +6sin(πt+φ)(N·m)摩擦阻力矩扰动下炮控系统高低向阶跃响应误差，阶跃值为100 mil;图6 给出该炮控系统对频率为1 Hz、幅值为100 mil 的谐波运动轨迹的跟踪误差，e 为位置误差。从图5 可见，FNSMC 系统具有较小的稳态误差，对外部扰动误差表现出更强的抑制性;FNSMC系统具有更快的响应速度。从图6 可以看出，CNSMC 系统的谐波跟踪误差约为±2%，而FNSMC系统的跟踪误差约为±0.4%，跟踪精度提高了约5 倍。

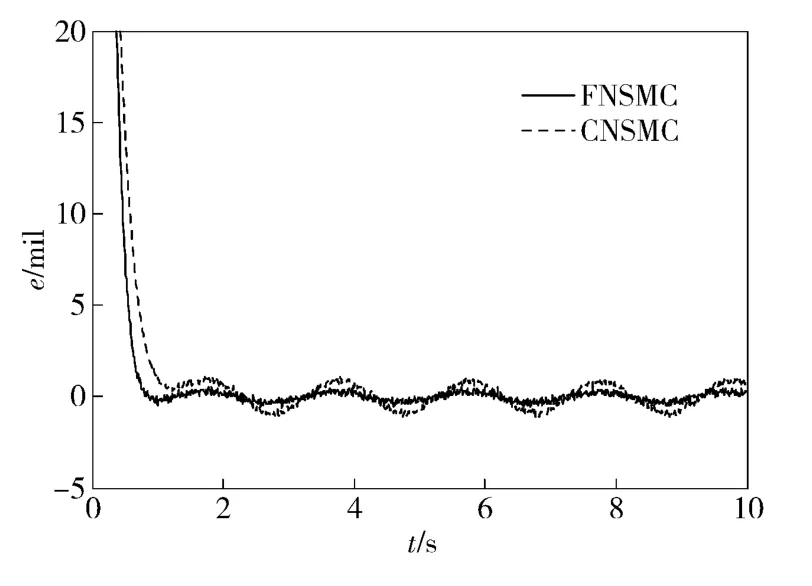
图5 调炮操作阶跃响应误差Fig.5 Step response errors

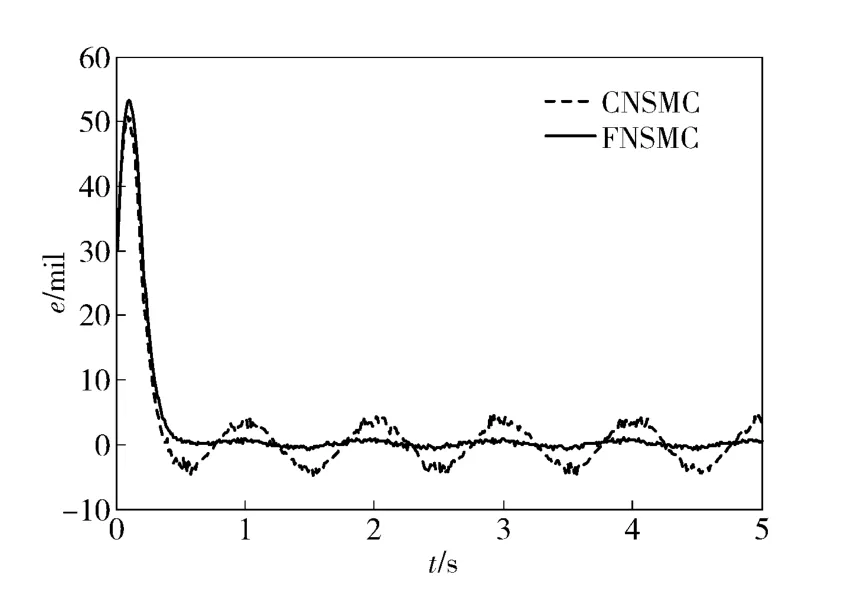
图6 调炮操作谐波轨迹跟踪误差Fig.6 Tracking errors of harmonic trajectory

阶跃响应及谐波跟踪试验结果表明，相对于CNSMC，本文提出之FNSMC 策略具有明显的优越性，表现出更强的鲁棒性及更高的跟踪精度，具有优异的动静态品质，适用于调炮控制。

5 结论

针对某顶置火炮高低向调炮控制系统存在的不确定性外部扰动及强非线性特征，本文提出了一种FNSMC 策略，并对其进行了数值仿真及半实物台架实验。所得出主要结论如下:

1)数值仿真结果表明:FOC 的引入使得FNSMC 系统能够更为快速平滑的趋近稳态，这将极为有效的抑制传统SMC 的抖振现象，提高控制系统的响应速度。同时，通过引入FOC，可以更为柔性的调整控制系统的收敛状态及动态特征，获得更优的动静态品质。

2)样机试验结果表明:较之CNSMC，本文所提出FNSMC 能更好的抑制外部扰动，表现出更强的鲁棒性;同时，FNSMC 的谐波跟踪精度较之CNFMC约能提高5 倍。将FNSMC 应用于炮控系统，能有效提高其调炮稳定性及精准度，具有应用前景。

References)

[1]马晓军，冯亮，袁东，等.坦克炮控系统非线性特性及自适应补偿控制[J].火力与指挥控制，2010，35(11):1 －5.MA Xiao－jun，FENG Liang，YUAN Dong，et al.Overview of adaptive compensation control of nonlinearity in tank gun control system[J].Fire Control ＆ Command Control，2010，35(11):1 －5.(in Chinese)

[2]冯亮，马晓军，闫之峰，等.坦克炮控系统自适应模糊滑模控制方法[J].电机与控制学报，2007，11(1):65 －69.FENG Liang，MA Xiao－jun，YAN Zhi－feng，et al.Method of adaptive fuzzy sliding mode control of gun control system of tan[J].Electric Machines and Control，2007，11(1):65 －69.(in Chinese)

[3]Fnaiech M A，Betin F，Capolino G A，et al.Fuzzy logic and sliding－mode controls applied to six－phase induction machine with open phases[J].IEEE Transactions on Industrial Electronics，2010，57(1):354 －364.

[4]Nguyen T N，Su S，Nguyen H T.Robust neuro－sliding mode multivariable control strategy for powered wheelchairs[J].IEEE Transactions on Neural Systems and Rehabilitation Engineering，2011，19(1):105 －111.

[5]Tsai C H，Chung H Y，Yu F M.Neuro－sliding mode control with its applications to seesaw systems[J].IEEE Transactions on Neural Networks，2004，15(1):124 －134.

[6]Zhou X Q，Zhu Z W，Zhao S X，et al.An improved adaptive feedforward cancellation for trajectory tracking of fast tool servo based on fractional calculus[C]∥Procedia Engineering.Dali:Elsevier，2011:315 －320.

[7]Ma C B，Hori Y.The application backlash of fractional order control to vibration suppression[C]∥Proceedings of the 2004 American Control Conference.Boston:IEEE，2004:2901 －2906.

[8]Tavazoei M S，Haeri M，Jafari S，et al.Some applications of fractional calculus in suppression of chaotic oscillations[J].IEEE Transactions on Industrial Electronics，2008，55(11):4094 －4101.

[9]Calderon A，Vinagre B，Feliu V.Fractional order control strategies for power electronic buck converters[J].Signal Processing，2006，86(10):2803 －2819.

[10]Efe M O，Kasnakoglu C.A fractional adaptation law for sliding mode control[J].International Journal of Adaptive Control and Signal Processing，2008，22(10):968 －986.

[11]Efe M O.Fractional order sliding mode control with reaching law approach[J].Turkish Journal Electrical Engineering and Computer Sciences，2010，18(5):731 －747.

[12]Delavari H，Ghaderi R，Ranjbar A，et al.Fuzzy fractional order sliding mode controller for nonlinear systems[J].Communications in Nonlinear Science and Numerical Simulation，2010，15(4):963 －978.

[13]王乃洲.基于分数阶微积分理论的滑模变结构控制[D].南京:南京林业大学，2010.WANG Nai－zhou.Research of sliding mode control based on fractional calculus[D].Nanjing:Nanjing Forestry University，2010.(in Chinese)

[14]高强，庞雷，杨国来，等.基于神经滑模的某顶置火炮自动装填调炮控制[J].机床与液压，2013，41(11):36 －38，63.GAO Qiang，PANG Lei，YANG Guo－lai，et al.Self－loading adjustment of a top－mounted gun based on a novel neural slide mode control[J].Machine Tool ＆ Hydraulics，2013，41(11):36 －38，63.(in Chinese)

[15]张碧陶，皮佑国.基于分数阶滑模控制技术的永磁同步电机控制[J].控制理论与应用，2012，29(9):1193 －1197.ZHANG Bi－tao，PI You－guo.Fractional order sliding－mode control for permanent magnet synchronous motor[J].Control Theory＆ Applications，2012，29(9):1193 －1197.(in Chinese)

[16]张碧陶，皮佑国.永磁同步电机伺服系统模糊分数阶滑模控制[J].控制与决策，2012，27(12):1776 －1780.ZHANG Bi－tao，PI You－guo.Fractional order fuzzy sliding mode control for permanent magnet synchronous motor servo drive[J].Control and Decision，2012，27(12):1776 － 1780.(in Chinese)

[17]Haddadnia J，Ahmadi M，Faez K.An efficient feature extraction method with pseudo－Zernike moment in RBF neural networkbased human face recognition system[J].Journal on Applied Signal Processing，2003，(9):890 －901.