一类不可微规划算法的线性收敛性

郑颖春， 王雪峰

(西安科技大学 理学院， 陕西 西安 710054)

0 引言

不可微优化(或非光滑优化)讨论具有不连续一阶偏导数的函数的极小化(或极大化)问题，在经济数学与其它一些实际问题中往往会遇到，近三十余年来，不可微优化的理论与方法有了很大的发展.作者Sachs.E在文献[1]给出了一种不可微优化的拟牛顿算法，作者Alexander.Shapiro， M.S.KIM，D.H.CHOI and Y.HWAN，Womersley.R.S分别在文献[2]、[3]、[4]中给出了合成函数的不可微优化算法，作者Israel Zang在文献[5]提出了一类有效的极小极大问题的算法.这些算法代表了不可微优化算法的发展方向，但都没有讨论算法的收敛速度，而本文将着重研究一类不可微优化算法的线性收敛性.

1 算法描述

本文主要讨论如下一类不可微最优化问题

式中f(x)在Rn中是局部李普希兹的[6，7,8].文献[9]已给出这类问题的一种有效算法，并且证明了该算法具有线性收敛性，文献[9]的算法和次梯度算法具有相同的收敛速度，本文借助文献[9]的证明方法证明了一般的次梯度算法都具有线性收敛性.

次梯度算法及收敛性可用以下定理描述：

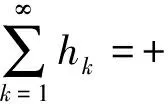
xk+1=xk-hk‖gf(xk)‖-1gf(xk)k=0,1,2,…

文献[9]给出了次微分集的外接长方体的概念，并证明了次微分集的外接长方体的中心元一定是一个次梯度，这时次梯度法可简化为：给定初始点x0，可以用迭代公式：

xk+1=xk-hk+1‖yk‖-1yk

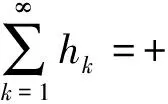
2 基本概念与基本引理

下面首先给出线性收敛及二阶方向导数的定义，然后证明几个积分中值定理.

定义1[10]设序列{x(k)}⊂Rn收敛于x*.

若存在常数ρ∈(0,1)，使得当k充分大时，

‖x(k+1)-x*‖≤ρ‖x(k)-x*‖

则称{x(k)}线性收敛于x*，或称{x(k)}的收敛速度是线性的.

定义2 (二阶方向导数)设f:Rn→R1是局部李普希兹函数，f′(x,d)对x也是局部李普希兹的，若极限

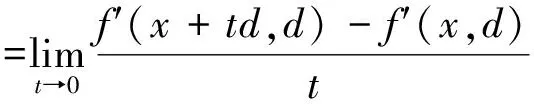
设x(t)是[0,T]上的n维连续且可微的向量函数，令φ(t)=f[x(t)]，不难证明φ(t)在[0,T]是绝对连续函数，故存在可积函数ω(t)使得

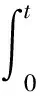
(1)

这里的积分是Lebsegue积分，并且几乎对所有的t∈[0,T]，有：

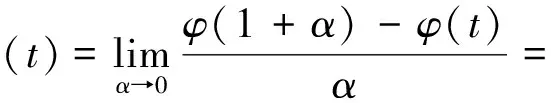
也就是说函数φ(t)几乎处处可微.

引理1 设函数f:Rn→R1在点x0是局部李普希兹的，则f在x0具有以下性质

∀v∈Rn.由(1)及引理1可知，

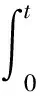
故

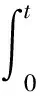
(2)

这就是一阶的积分中值定理.

引理2 设f:Rn→R1是局部李普希兹的，f′(x,d)对x也是局部李普希兹的，则下列积分中值定理成立：

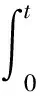
(3)

f(x+λd)=f(x)+λf′(x,d)

(4)

证明：(3)式由二阶方向导数的定义立即可得.

以下证明(4)

由(2)式可知

故

f(x+λd)-f(x)-λf′(x,d)

即

由于[11]

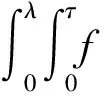
所以(4)式成立.

引理3 若存在m,M1,K使得：

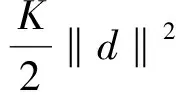
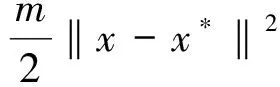
‖ξ(x)‖≤m‖x-x*‖，其中M=M1+K,ξ(x)满足<ξ(x),x-x*>=f′(x,x-x*).

由引理2及定积分的保序性易证这个引理，这里从略.

引理4 设φ(λ)在[0,b]上是局部李普希兹的，且φ′(0,1)<0,(φ′(0,-1)<0),若φ(λ)在[0,b]上的极小点λ*∈(0,b)，则有

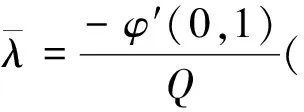
其中Q是φ″(0,1),(φ″(0,-1))的正上界.

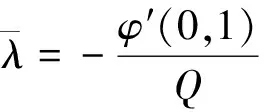
3 算法的线性收敛性

下面用上述引理来证明算法的线性收敛性.

‖xk+(λk+δ)dk-x*‖=‖xk+1-x*+δdk‖<ε

考虑对φ(λ)=f(xk+λdk)在区间[0,λk+δ]上应用引理4，并注意dk的取法，

φ′(0,1)=f′(xk,dk),

φ′(λ,1)=f′(xk+λdk,dk),φ″(λ,1)

=f″(xk+λdk,dk)，由于f″(xk+dk,dk)有界，所以φ″(λ,1)有界.由引理3知φ(λ)在[0,λk+δ]上的整体极小点λk满足：

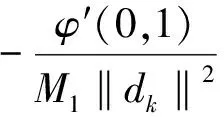
其中:M=M1+K,〈ξ(xk),dk〉=f′(xk,dk) ,α(xk)∈(0,1).

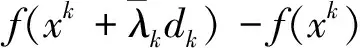
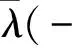
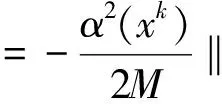
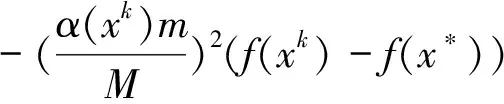
于是f(xk+1)-f(x*)≤θ[f(xk)-f(x*)]，其中

θ=(α(xk)mM)2〗12，则有：

f(xk+1)-f(x*)≤θ2(f(xk)-f(x*))

≤…≤θ2k(f(x1)-f(x*))

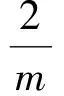
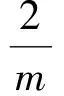
即‖xk+1-x*‖≤sθk，(k=1,2,…),其中

4 数值例子

下面用场址的合理选定问题来验证算法的可行性.假设要选定一个供应中心，(例如超市、影院、奶站等)的位置，该中心为m个具有固定位置(ai,bi),i=1,2,…，m的用户服务，而中心的定位准则是使中心到用户的某个距离函数取最小等，试求供应中心的位置[12].

为此需先建立该问题的数学模型，设供应中心的位置为(x,y)可建立以下数学模型：

如给定

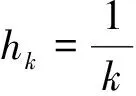
距离总和为10.667 4，中心到用户的距离分别是：2.777 73,3.777 91,4.111 10.

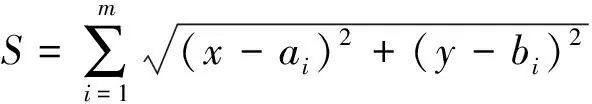
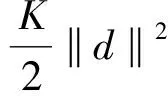
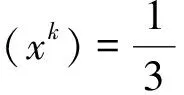
即有‖xk+1-x*‖ ≤sθk,(k=1,2,…)

从而算法具有线性收敛性.

5 结束语

本文给出了二阶方向导数的定义，并在此基础上证明了不可微情形下的一阶及二阶积分中值定理，这些中值定理和可微情形是相似的，进而证明了一类不可微优化算法具有线性收敛性，数值例子表明算法是有效的，并具有线性收敛性.

[1] Sachs E.Quasi-newton methods foraclass of nonsmooth constrained oplmization problems[J].Lectur Notesin Contraland InformationSci,1982，38(4):42-45.

[2] Alexander,Shapiro.On a class of nonsmooth composite functions[J].Mathematics of Operations Research,2003，28(4)，677-692.

[3] M.S.KIM,D.H.CHOI,Y.H.WANG.Composite nonsmooth optimization using approximate generalized gradient vectors[J].Journal of Optimiaztion Theory and Applications,2002,112(1),145-165.

[4] Womersley.R.S,Fletcher.R.An algorithm for composite nonsmooth optimization problems[J].Journal of Optimization Theory and Applications,1986，48(2),493-523.

[5] Israel Zang.A smoothing-out technique for min-max optimization. Math Prog,1980,19(2):61-76.

[6] Rokafellar.R.T.Convex analysis[M].Princetion:New Jersey,1970:56-112.

[7] Shor.N Z.Minimization Methods for Nondiffenrentiable Function[M].New York:Springer-Verlag,1979:231-244.

[8] F.H.Clarke.Nonsmooth nalysis and optimization[M].New York: Wiley-Interscience,1983:37-41.

[9] 王雪峰.基于次微分集的外接长方体的不可微优化算法[J].西北大学学报,2009，39(2):196-198.

[10] 袁亚湘，孙文瑜.最优化理论与方法[M].北京：科学出版社，2005.

[11] 华东师范大学数学系.数学分析[M].北京：高教出版社，2002.

[12] 阳明盛，罗长童.最优化原理、方法及求解软件[M].北京：科学出版社，2006:240-242.