不同工况下分隔式双流道涡轮非稳态性能的研究

范厚传，刘云岗，王 航，朱智富，刘 臻

（1.山东大学能源与动力工程学院，山东 济南 250061；2.康跃科技股份有限公司，山东 寿光 262718）

涡轮增压技术作为一项提高发动机动力性和燃油经济性的有效措施，正越来越受到重视，尽可能地利用发动机废气能量对进气道新鲜空气做功，是涡轮增压技术发展的动力。从发动机的工作原理可知，发动机的排气过程是一个周期性的非稳态过程，安装在排气歧管后的涡轮增压器的进气也是非稳态过程［1］，所以，目前普遍采用的稳态研究方法不能更好地反映增压器涡轮的实际工作过程。

涡轮的非稳态研究开始于20世纪60年代，早期的研究主要专注于试验［2－4］，随着科学技术的发展，涡轮非稳态研究手段不断丰富，PIV（粒子图像测速仪）、LDV（激光多普勒测速仪）等新技术的应用［5－6］使涡轮非稳态参数的测量更为精确，而计算机技术的发展使采用模拟计算方法研究涡轮非稳态成为可能，涡轮的研发成本因此大幅降低。

本研究在文献［7］的基础上，采用模拟方法对180°分隔式双流道涡轮进行非稳态特性研究，探索在不同发动机工况下涡轮的实际工作过程，希望找出涡轮非稳态特性规律及原因，以较为全面地评估涡轮工作性能。

1 研究对象和研究方法

研究对象是匹配某6缸柴油机的JP80S增压器双流道涡轮，其搭配的蜗壳为带双旁通放气阀的180°分隔式进气双流道蜗壳，涡轮叶轮进口直径为80mm，涡轮流道分为内流道和外流道，涡轮流道的整体布置见图1。研究状态为双旁通放气阀全关时的状态。增压器布置在柴油机的中间位置，柴油机自由端为第1缸，第1，2，3缸的排气歧管连接涡轮内流道，第4，5，6缸的排气歧管连接涡轮外流道。

研究方法为数值模拟方法，计算平台为Ansys CFX软件。首先从试验数据出发，建立计算模型，利用AVL Boost软件得到涡轮输入的非稳态边界条件；然后进行不同发动机转速的外特性工况下的涡轮非稳态计算，得到涡轮非稳态结果，并进行分析；最后，从微观流场的角度去探索涡轮非稳态特性的形成机理。

2 计算模型的建立与非稳态边界条件

2.1 计算模型的建立与验证

在划分好模拟计算所需的涡轮网格之后［8］，根据涡轮的稳态台架试验数据，确定相关的物性参数［9］及模型进出口位置。计算的湍流模型选用SST模型，数学模型选用雷诺平均 N－S方程组［10－11］；涡轮流道的各壁面均视为绝热、光滑、无滑移的理想壁面，流体选用理想气体。

图2示出稳态条件下转速为80 000r/min时涡轮流量与输出功率的试验验证结果，验证方法参照文献［7－8，12］。从图2可以看出，涡轮的流量参数和输出功率的模拟值和试验值的走向基本一致。其中，涡轮流量参数模拟值和试验值的最大相对误差为2.1%，涡轮输出功率模拟值和试验值的最大相对误差为2.8%，误差值在允许的范围内，所以，认为本研究所建立的计算模型是有效的。

2.2 涡轮输入的非稳态边界条件

由于所研究蜗壳带双旁通放气阀，根据试验，当发动机转速高于1 600r/min时，双旁通放气阀将处于开启状态，计算条件应设置在发动机转速等于或小于1 500r/min的工况下。所以，计算工况分别选择 发 动 机 处 于 800r/min，1 200r/min 及1 500r/min时 的 外 特 性 工 况 （见 图 3），其 中1 500r/min为发动机最大扭矩转速，各工况和增压器的对应情况见表1。

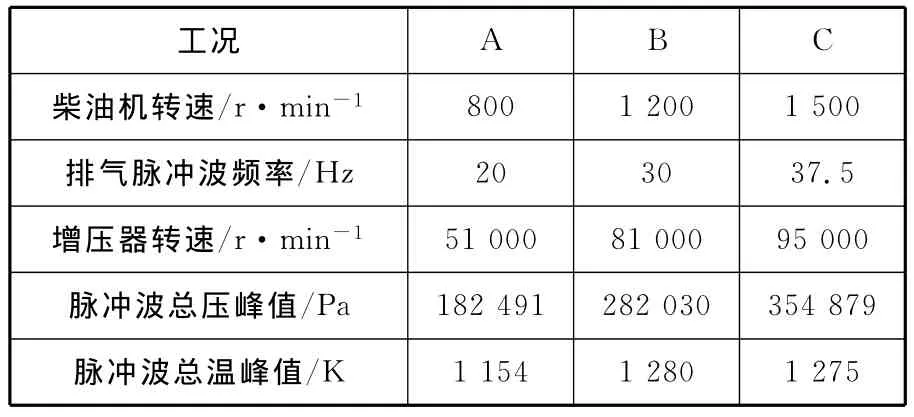
表1 柴油机工况和增压器工况的对应表

涡轮所匹配的主机为6缸柴油机，其发火顺序为1—5—3—6—2—4，排气歧管输出6个具有相似形状的排气脉冲波，涡轮非稳态结果呈现6个重复的相似圈，因此只取各工况下第1缸的排气脉冲波进行研究。涡轮模型进口的非稳态边界条件由AVL Boost软件模拟该6缸柴油机的实际工作过程而得，涡轮蜗壳内外流道的非稳态进口边界条件的波形见图4。每个涡轮进口分别与3个气缸的排气道相连，因此，在1个柴油机工作循环内，当柴油机第1缸的排气脉冲波波峰进入涡轮外流道进口处时，涡轮内流道进口处的脉冲波基本处于波谷平缓区，所以图4中各工况外流道输入的总压和总温要高于内流道输入的对应值。

3 结果分析

图5至图7分别示出涡轮非稳态效率对比、涡轮输出功率对比及流量参数对比，其中，涡轮非稳态效率参考文献［7］。从3个图可以看出，每个工况点的各种涡轮非稳态特性曲线基本呈不规则的、完整“圈”的形状，而且这些非稳态特性圈对准稳态曲线形成封装效果［13］。这些非稳态效率特性圈总体上分为上半部分和下半部分，分别对应输入脉冲波的波前或波后，而上下两部分曲线所反映出的涡轮性能差异即为涡轮非稳态的充盈和排空效应［13］。

由图5可以看出：A工况的涡轮效率圈的充盈段和排空段相差最大，效率波动很大；随着转速的升高，这种差异不断减小，波动也减小；到C工况时涡轮非稳态效率圈已较为规则了，与准稳态曲线的差异相对减小，充盈段和排空段曲线变化平缓。

表2列出A，B，C 3个工况性能的脉冲循环均值。从表2得知：C工况时的涡轮非稳态脉冲循环平均效率为0.767 8，高于其他两个工况，A工况的整体效率最小；涡轮脉冲平均效率出现随柴油机转速升高而逐步升高的趋势。

由图6和图7可见，随着脉冲频率和脉冲峰值的上升，涡轮特性圈整体不断上升，也就是涡轮的输出功和流通能力不断提高，表2的相关数值也说明这点，这主要与涡轮进口的脉冲波密度和脉冲波能量有关。A工况的涡轮非稳态流量参数曲线和涡轮非稳态输出功率曲线的充盈段与排空段的差异最小，即充盈和排空效应最弱，与对应的涡轮准稳态曲线最接近；随着转速上升，非稳态曲线与准稳态曲线的差异不断增大，即充盈和排空效应也越加明显，这和文献［13］所阐述的结论是吻合的。

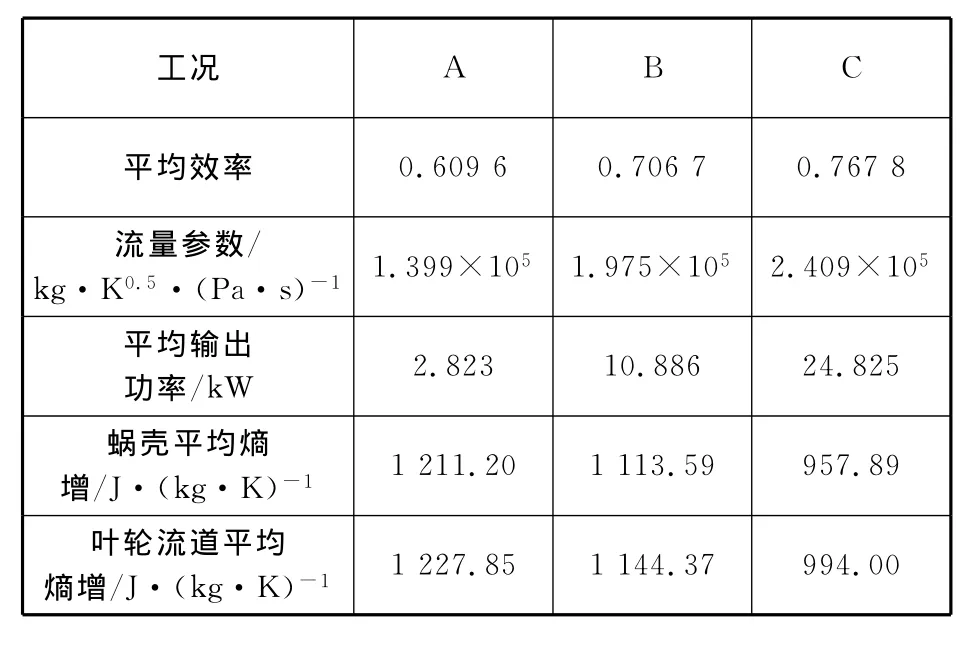
表2 3个工况性能的脉冲循环均值比较

4 流场分析

由于所研究的3个工况涡轮输入的脉冲频率、脉冲峰值及涡轮转速均不一样，所以在进行流场分析时分别取脉冲波平均值附近的点为研究对象，这样A，B，C工况的分析对象分别取膨胀比为1.24，1.66及2.25附近的点，按充盈段和排空段各取1个点的原则，共有6个点。

图8示出3个工况的蜗壳流道的流线分布。由图8可以看出，各工况排空段的蜗壳出口速度均大于充盈段，在压力能相同情况下，排空段的蜗壳出口处有更大的动能，使得更多的能量转化为涡轮转子的扭矩，从而排空段的效率大于充盈段。而随着转速的升高，蜗壳内流速也随之升高，C工况的流速最高。

图9示出3个工况的蜗壳熵增分布。从图9得知，各工况排空段的熵增均大于充盈段，主要原因是排空段的速度较大，流动摩擦损失大；随着转速的升高，蜗壳的熵增反而下降，C工况的整体熵增最小，表明随着转速的升高，蜗壳流道内气流流动更顺畅，流动损失减小。

图10示出3个工况的涡轮叶轮流道截面速度矢量。由图10可知，速度矢量分布规律与蜗壳流线速度分布规律相似：排空段的叶轮进口速度大于充盈段；随着转速的升高，叶轮进口速度上升。关于这3个工况的叶轮进口速度，本研究列出1个脉冲循环内的变化趋势（见图11）：在所有膨胀比下，排空段的叶轮进口速度都明显大于充盈段；随着转速的升高，叶轮进口的整体速度不断上升。图10还显示，A工况时在叶片吸力面附近出现了气流与叶片分离现象，随着转速的升高，分离区域逐渐减小。

图12示出各工况下80%叶轮流道高度截面上的熵增分布。从图12可以看出，叶轮流道内排空段的熵增大于充盈段，随着转速的升高，熵值不断减小，C工况的熵值最小，这与图10所示的气流分离程度及影响区域有关。

图13示出脉冲循环蜗壳平均熵增，图14示出脉冲循环叶轮流道平均熵增。从这两个图可以看出，排空段熵增大于充盈段熵增，叶轮流道内熵增大于蜗壳流道内的熵增，叶轮流道内的充盈段与排空段的熵增差值明显大于蜗壳流道内的相应差值。从图中还可以看出，随着转速的升高，蜗壳和叶轮流道的整体熵值不断减小，C工况熵值最小，与表2一致；并且充盈段和排空段的差值也不断减小，使得熵增的充盈与排空效应减弱，而这是脉冲频率、脉冲峰值和涡轮转速共同作用的结果。

5 结论

a）在所研究范围内，各工况下的涡轮非稳态特性均呈现出充盈和排空效应，随着柴油机转速的升高，涡轮脉冲循环的平均效率、平均输出功率和平均流量参数不断上升，对废气能量的利用率逐渐升高；

b）随着柴油机转速的升高，涡轮效率的充盈和排空效应逐渐减弱，与准稳态值越接近，对废气能量的利用率也越稳定；而涡轮的非稳态流量参数和输出功率的充盈和排空效应逐渐加强，逐渐偏离准稳态值；

c）随着柴油机转速的升高，涡轮的整体熵增呈减小趋势，而且熵增的充盈和排空效应逐渐减弱，低转速涡轮熵增大的主要原因是叶片吸力面附近的气流分离程度强及影响区域大。

［1］ 施 新，马朝臣.车用增压器涡轮非稳态流动特性研究进展［J］.车用发动机，2003（5）：36－39.

［2］ Wallace F J，Blair G P.The pulsating－flow performance of inward radial－flow turbines［J］.ASME，1965，65（gtp－21）：1－19.

［3］ Benson R S，Scrimshaw K H.An Experimental Investigation of Non－Steady Flow in a Radial Gas Turbine［J］.Proceedings of IMechE，1965，180（3）：66.

［4］ Miyashita T，Tomita T，Ishihara D.Performance of inward radial flow turbine under unsteady flow conditions［J］.Ishikawajima－Harima Engineering Review，1973，13（3）：259－269.

［5］ 李 军，苏 明.涡轮叶栅非定常流动的PIV实验［J］.华中科技大学学报：自然科学版，2007（S1）：133－135.

［6］ Marina Ubaldi，Pietro Zunino.An experimental study of the unsteady characteristics of the turbulent near wake of a turbine blade［J］.Experimental Thermal and Fluid Science，2000，23：23－33.

［7］ 范厚传，王 航，刘云岗，等.脉冲全周进气和非全周进气涡轮性能比较的数值研究［J］.车用发动机，2012（4）：25－28，33.

［8］ Mohammed Hamel，Miloud Abidat，Sid Ali Litim.Investigation of the mixed flow turbine performance under inlet pulsating flow conditions［J］.Comptes Rendus Mecanique，2012，340：165－176.

［9］ 张家荣，赵廷元.工程常用物质的热物理性质手册［M］.北京：新时代出版社，1987.

［10］ Gerolymos G A，Bréus J P.Computation of Unsteady Nozzle Flow Resulting from Fluctuating Back－Pressure Using Euler Equations［J］.Aerospace Science and Technology，1998（2）：91－105.

［11］ John D.Anderson.Computational Fluid Dynamics［M］.New York：McGraw－Hill，1995.

［12］ Peter Newton，Colin Copeland，Ricardo Martinez－Botas，et al.An audit of aerodynamic loss in a double entry turbine under full and partial admission［J］.International Journal of Heat and Fluid Flow，2012，33：70－80.

［13］ Srithar Rajoo，Alessandro Romagnoli，Ricardo F.Martinez－Botas.Unsteady performance analysis of a twinentry variable geometry turbocharger turbine［J］.Energy，2012，38：176－189.