发动机轴承并发故障信号盲源分离方法研究

李志宁，孙宜权，2 ，张英堂，田 昊，范红波

（1.军械工程学院，河北 石家庄 050003；2.66267部队，河北 石家庄 050081）

发动机的轴承故障影响着发动机的经济性、动力性及行驶安全性。由于发动机结构复杂，轴承故障特征微弱，在其他信号干扰下较难被检测到，如何发现轴承故障并作出诊断，对于减小经济损失和排除安全隐患具有重要的意义。目前，在发动机轴承故障诊断中，已有较多的信号分析方法应用于单一故障诊断，且效果较好［1］，而对于并发故障，由于故障信号之间的耦合与调制，导致诊断的难度增加、准确率下降［2］。

盲源分离（BSS）算法为发动机轴承并发故障信号分离提供了一种有效的方法，但是，目前在发动机振动信号盲源分离中，通常假设观测信号的数目不小于源信号的数目，而在实际应用中，这个假设往往是不成立的。对于欠定盲源分离，已有的研究基本上是基于源信号的稀疏表示，借助聚类算法实现。由于柴油机本身的复杂性及其工作环境的多样性，从柴油机上获取的振动信号必然是多个振源信号以未知的混合形式混叠而成的复杂信号，所以对于柴油机振动信号，源信号的稀疏性假设并不一定成立［3］。

本研究提出了基于平行因子分析（PARAFAC）的发动机轴承并发故障信号盲分离方法，利用求得的信号传播路径响应函数构造了虚拟观测信号，将盲源分离从欠定转变为适定或超定，然后采用自适应PARAFAC方法解决柴油机轴承并发故障信号相互耦合的故障模式。

1 平行因子分析方法

平行因子分析概念始于心理实验学领域的数据分析，是一种多维低秩分解方法。Caroll等人发展了平行因子分析模型，用于无线通信和盲源分离等领域［4］。本研究以3维数据为例，数据X∈CI×J×K集可以分解为M 个秩为1的3维矩阵之和，如式（1）所示［5］：

式中：am∈CI×L；bm∈CJ×L；cm∈CK×L；表示张量积。X中的元素可表示为

若A＝［a1，…aM］∈CI×M，B＝［b1，…bM］∈CJ×M，C＝［c1，…cM］∈CK×M，称矩阵A，B，C为X 的模式矩阵。为了讨论X的分解是否唯一，引入定义1和定理1。

定义1［6］：若矩阵A的任意kA个列线性独立，则最大的kA值称为矩阵A的Kruskal秩，简称k秩。

定理1［7］：A，B，C 的定义见式（2）。存在 K 个矩阵Xk＝ADk（C）BT，k＝1，2，3，…K，Dk（C）是对矩阵C的第k行进行对角化处理；若kA＋kB＋kC≥2（M＋1），则分解得到的矩阵估计值A，BT，C各列排列次序与比例因子不确定外，可唯一确定。

2 欠定盲源分离算法

2.1 信号传播路径响应函数预测

本研究利用PARAFAC方法，预测传播路径响应函数，从而消除延迟滤波对观测信号的影响。卷积混合信号的数学描述见式（3）［8］：

式中：S（t）＝［s1（t），s2（t），…sI（t）］T为I个源信号构成的向量；X（t）＝［x1（t），x2（t），…xJ（t）］T为J个混合信号构成的向量；混合矩阵H为J×L维矩阵；＊为卷积运算；L为传输路径响应长度。

为预测传播路径响应函数，将观测信号变换到频域分析。式（3）经离散傅里叶变换后为［8］

式中：频率标志f＝1，…F；p为数据段标志；X（f，p）＝ ［x1（f，p），…xJ（f，p）］T；S（f，p）＝［s1（f，p），…sI（f，p）］T；H（f）的第i列代表第i 个源信号在频率f处的传播路径响应。

假设每一个观测信号包含N个采样点，将其分割成P个不交叠的数据段，每个数据段包含NP＝ent（N/P）个数据点，用p＝1，…P 标志数据段，当采样频率为Fs时，每个数据段持续的时间Tp＝（Np/Fs）。在此基础上，J×J维自相关矩阵Rx（f，p）＝E［X（f，p）XH（f，p）］可写为

式中：Rs（f，p）＝E［S（f，p）SH（f，p）］为p 数据段，频率为f的源信号自相关矩阵。式（5）展开可写为

记Rx（f，p）为γ（x）j1，j2，p（f），其中，j1＝1，…J，j2＝1，…J，p＝1，…P；H（f）中的元素记为hj，i（f）；构建一个P×I维矩阵C（f），其中的元素记为cp，i（f），代表Rs（f，p）矩阵对角线上第i个元素。根据式（6）γ（x）j1，j2，p（f）可写为

与式（2）对比可知，式（7）为PARAFAC分解，其中，I为Rs（f，p）的秩。根据PARAFAC方法，最终可得唯一解｛H（f），f＝1，…F｝，但各列解的排列次序与比例因子不确定。通过对排列次序与比例因子进行自适应调整，从而解决上述不确定问题，称为自适应PARAFAC算法，具体过程参考文献［5］。

2.2 通道虚拟方法

考虑到观测信号受传播路径的影响，图1示出了源信号S（f，p）至观测信号X（f，p）的传播过程，其中路径响应函数H（f）中的元素简记为hj，i。

从图1可知，当路径响应函数各列解的排列次序与比例因子正确时，观测信号为各通道传感器拾取的信号；当传播路径冲击响应函数各列解随机排列次序时，观测信号可看作虚拟通道传感器拾取的信号，称之为虚拟观测信号。

2.3 源数估计

为实现信号欠定盲分离，首先要估计系统的源信号数。提出了虚拟观测信号与主分量分析（PCA）结合的源数估计方法［9］。

利用通道虚拟方法得到虚拟观测信号，将观测信号与虚拟观测信号组成新的多维观测信号XN（t）＝［x1（t），…xJ（t），x1V（t），x2V（t），…］T，其中，［x1V（t），x2V（t），…］T为虚拟观测信号，解决了源信号数大于观测信号数的难题。

PCA可以确定信号和噪声子空间的维数，假设将XN（t）∈Rm建模成

式中：H∈Rm×n是一个列满秩混合矩阵，且m＞n；S（t）∈Rn是一个零均值高斯源，其协方差矩阵Rss＝E｛S（t）·SH（t）｝；V（t）∈Rm是高斯零均值噪声，其协方差矩阵Rw＝σ2vIm。而且，S（t）与V（t）不相关。由上述假设可知，XN（t）的协方差矩阵可表示为

式中：H·Rss·HH＝Vs·Λs·VHs，Vs包含与n个主特征值Λs＝diag｛λ1≥λ2≥λ3≥…≥λn｝对应的特征向量；VN包含（m－n）个对应于噪声特征值ΛN＝diag｛λn＋1，λn＋2，…λm｝＝σ2vIm－n的特 征 向 量。理 论上Rxx的（m－n）个最小特征值等于σ2v，因此，从最小特征值的重复个数得到信号子空间的维数。但是在实际应用中，样本数是有限的，得到的最小特征值一般是不同的。为能得到信号自空间的维数，引入Bayesian信息准则［9］：

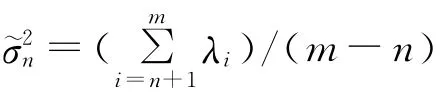
2.4 算法仿真研究

发动机振动特性比较复杂，无法准确描述。通常情况下，可简单用多个单自由度弹簧－质量－阻尼系统模型描述［8］。对上述系统物理模型进行力学分析得到：

式中：M为系统质量块的质量；K为系统的弹性系数；C为系统的阻尼系数；X（t）为系统产生的位移；F（t）为与发动机转速相关的激励力。F（t）可表示为

式中：mu为转轴不平衡质量；ru为转轴不平衡质量距离转轴轴心的距离；ω为转轴的角速度。

本研究以振动加速度的形式采集信号，通过改变式（12）中的ω（分别为100r/min，160r/min，120r/min）产生3个不同的激励力，进而得到3个源信号（图2前3个），最后1个源信号（图2最后1个）通过下式得到：

通过设置源信号与观测信号间的传播路径冲击响应［5］，并利用卷积运算得到3个观测信号（图3的前3个观测信号），通过虚拟通道的方法，得到4个虚拟观测信号（图3的后4个观测信号）。各观测信号的特征值贡献率见图4。从中可以看出，前4个特征值贡献率之和接近100%，后3个特征值贡献率很小，进一步由Bayesian信息准则可以判断，仿真信号的源数估计为4，与实际的源信号数一致。

以实际观测信号与虚拟观测信号组成新的观测信号进行盲源分离，使盲源分离从欠定变为适定或超定。图5示出了分离信号，对比图2可知，观测信号得到较好的分离。

3 发动机曲轴连杆轴承并发故障振动信号盲分离

3.1 试验系统相关设置

试验在东风EQ6BT 6缸四冲程发动机上进行，为得到反映曲轴连杆轴承并发故障振动信号，减少其他缸的振动干扰，根据文献［10］可知，传感器最佳安装部位为发动机缸体和油底壳结合处左右侧及油底壳处。在这3个部位安装加速度振动传感器（见图6）。振动信号在加速状态下同步采集，采样频率为12.8kHz，采样点数为16 384，采集时利用设定的转速（1 800r/min）触发采集。试验设置的曲轴轴承与连杆轴承技术状态见表1［2］。本研究是在参考文献［2］的基础上对轴承并发故障诊断方法进行更深入的研究。

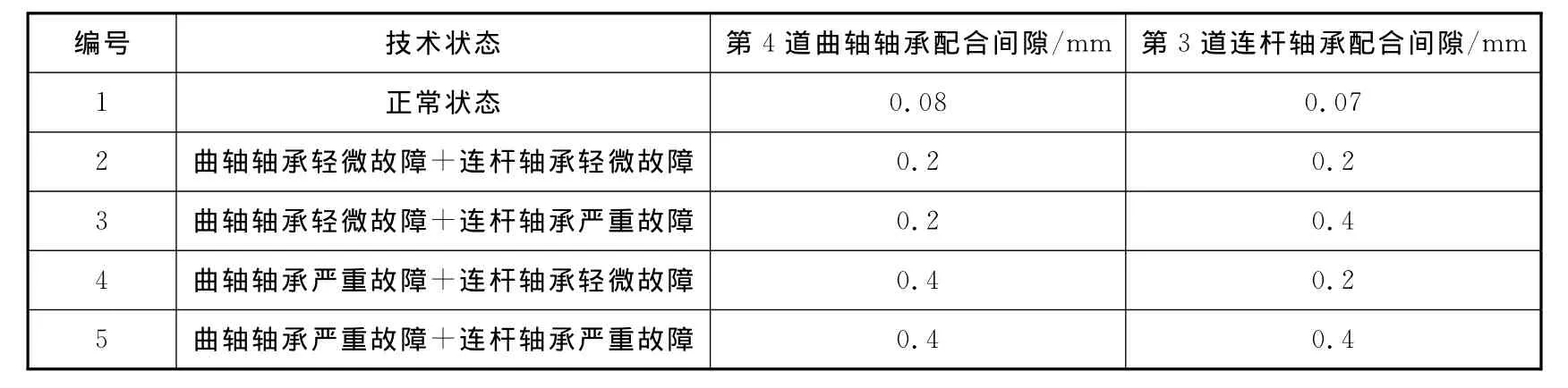
表1 曲轴连杆轴承并发故障参数设置

3.2 轴承并发故障振动信号盲分离

试验安装的3个传感器离轴承并发故障振源最近，测量得到的信号对轴承配合间隙变化敏感［11］。由于发动机燃爆振动信号的主要频率为1kHz，3kHz，5kHz附近［12］，轴承故障信号特征频率主要分布在3kHz以下低频段［2］，为减弱燃爆振动信号的干扰，对观测信号进行低通滤波，正常状态下滤波后的观测信号见图7（前3个为实际观测信号，后2个为虚拟观测信号），源数估计为5。

图8示出了该观测信号的频谱，图9示出了正常状态分离得到的时域信号，图10示出了其分离信号的频谱，由于篇幅有限，在此只列出其他技术状态的频谱图，图11至图14分别对应曲轴轴承轻微故障＋连杆轴承轻微故障频谱、曲轴轴承轻微故障＋连杆轴承严重故障频谱、曲轴轴承严重故障＋连杆轴承轻微故障频谱、曲轴轴承严重故障＋连杆轴承严重故障频谱。

从图8可以看出，对于轴承并发故障振动信号，即使观测信号离振源很近，也无法从频谱中获取有效的特征信号，主要由于轴承并发故障振动是微弱信号，淹没在其他信号中。通过自适应PARAFAC算法，得到分离信号，并得到它的频谱分布。已有的研究表明，发动机加速运转时，当转速为1 800r/min时触发采集，曲轴轴承故障的特征频率段在1 500Hz附近，连杆轴承故障的特征频率段在1 000Hz附近［13］。由图11可知，分离信号1与信号5的能量分别集中在1 414Hz和2 516Hz附近，其中分离信号1反映了曲轴轴承故障的特征频率分布；由于2 516Hz为1 000Hz附近频率和1 500Hz附近频率的和频，因此，分离信号5反映了连杆轴承和曲轴轴承故障的特征频率分布。由图12可知，分离信号2与信号4的能量分别集中在1 629Hz和2 274Hz附近，其中分离信号2反映了曲轴轴承故障的特征频率分布；由于2 274Hz为1 000Hz附近频率的倍频，因此，分离信号4反映了连杆轴承故障的特征频率分布。由图13可知，分离信号2与信号5的能量分别集中在2 168Hz和625Hz附近，由于2 168Hz为1 000Hz附近频率的倍频，因此，分离信号2反映了连杆轴承故障的特征频率分布；由于625Hz为1 500Hz附近频率和1 000Hz附近频率的差频，分离信号5反映了连杆轴承和曲轴轴承故障的特征频率分布。同理易知，图14中，分离信号1与信号4反映了曲轴轴承和连杆轴承故障的特征频率分布。曲轴轴承和连杆轴承的故障特征频率来自经验值，并没有计算公式可参考。

由上述分析可知，虽然自适应PARAFAC方法可消除并发故障信号间的耦合，但对于振源较多、故障模式复杂、耦合严重的信号盲分离，各工况下分离信号的频谱分布和文献［13］的特征频率分布并非完全一致，分离信号中包含了故障特征频率的倍频、和频、差频，其余各谐波为其他频率的非线性组合，根据以上征兆，可诊断发动机轴承出现了并发故障。

4 结论

a）基于平行因子分析法，实现了信号传播路径响应函数的预测，并以此构造了虚拟观测信号，使盲源分离从欠定变为适定或超定；

b）针对信号传输延时滤波导致盲源分离信号的难题，利用自适应PARAFAC算法得到的分离信号准确诊断出曲轴轴承和连杆轴承耦合故障，为诊断发动机轴承并发耦合故障提供了一种新方法；

c）为诊断发动机每缸所对应的曲轴和连杆轴承的并发故障，需安装较多的振动加速度传感器，并且提出的故障诊断方法需人工判断，如何实现故障诊断的自动化仍需进一步研究。

［1］ 田 昊，唐力伟，田 广.基于盲源分离的齿轮箱复合故障诊断研究［J］.兵工学报，2010，31（5）：646－649.

［2］ 梅检民，张玲玲，肖云魁，等.基于高阶累积量的轴承并发故障振动信号分析［J］.内燃机学报，2011，29（4）：327－331.

［3］ 毋文峰，陈小虎，苏勋家.基于经验模式分解的单通道机械信号盲分离［J］.机械工程学报，2011，47（4）：13－15.

［4］ 梁军利，冀邦杰，赵 峰，等.一种基于平行因子分析的近场 源 定 位 新 方 法 ［J］.电 子 学 报，2007，35（10）：1909－1914.

［5］ Nion D，Mokios K N，Sidiropoulos N D，et al.Batch and Adaptive PARAFAC－based Blind Separation of Convolutive Speech Mixtures［J］.IEEE Trans.on Audio，Speech and Language Processing，2010，18 （6）：1193－1207.

［6］ Sidropoulos N D，Giannakis G B.Parallel factor analysis in sensor array processing［J］.IEEE Trans Signal Processing，2000，48（8）：2377－2388.

［7］ Sidropoulos N D，Giannakis G B，BIOR.Blind PARAFAC receivers for DS－CDMA systems［J］.IEEE Trans Signal Processing，2000，48（3）：810－823.

［8］ LI W，Gu，BALL A D，et al.A study of the noise from diesel engines using the independent component analysis［J］.Mechanical System and Signal Processing，2001，15（6）：1165－1184.

［9］ 贠亚男，许明圣.未知信源个数的自适应盲信号分离算法［J］.科学技术与工程，2011，32（11）：7931－7933.

［10］ 肖云魁，李世义，王建新，等.基于小波包——AR谱技术提取柴油发动机曲轴轴承故障特征［J］.北京理工大学学报，2004，24（6）：508－511.

［11］ 肖云魁，曹亚娟，吴 晓，等.用循环谱理论分析发动机曲轴轴承加速振动信号［J］.振动、测试与诊断，2008，28（2）：117－121.

［12］ 史玉鹏，刘建敏，许世永，等.基于缸盖振动的柴油机喷油、燃烧信息检测研究［J］.车用发动机，2011（3）：74－76.

［13］ 赵慧敏.发动机非稳态振动信号分析与智能故障诊断研究［D］.天津：天津大学，2010.