车用空压机蜗壳优化设计研究

杨国蟒 胡余生 陈 彬 宣卫豪 肖 勇

（1.珠海格力电器股份有限公司；2.广东省高速节能电机系统企业重点实验室）

0 引言

车用空压机是将环境大气提升至一定压力，并输送给终端的一种设备。空压机的蜗壳是用来收集气体，将气体动能转化为压能，并引向终端的重要部件。蜗壳对于整个空压机效率以及稳定工作范围都有很大的影响，深入了解蜗壳内部流场以及舌部对于空压机性能的影响是非常有必要的。但是由于空压机内蜗壳气体流动相当复杂，目前相关的研究并不多，现有的文献主要分为蜗壳结构的理论设计[1-3]，蜗壳内部流场的分析[4-10]和“转-静”相互干扰的研究[11-13]。但是，这些研究都是针对蜗壳的某一点进行的，不够全面，本文在这些研究的基础上，用数值分析系统地研究了蜗壳不同结构参数对蜗壳性能的影响，并从流场的角度总结了影响蜗壳性能的一般规律，为后续的蜗壳设计提供指导。

1 物理模型和计算方法

研究对象为某离心空压机，设计转速120000rpm，叶轮外径61mm，该空压机采用无叶平行壁板扩压器。采用TurboGrid 划分叶轮网格，如图1(a)所示，然后旋转复制生成整个叶轮的网格。无叶扩压器采用结构网格，蜗壳结构比较复杂，采用适应性较好的四面体网格，最后进行网格装配，形成整个流体域网格，如图1(b)所示，为减小网格数对计算结果的影响进行网格无关性验证（图2），当网格数量增加到135万时，效率基本不再变化，并结合计算的时效性，最终确定计算域网格数量为135万。

图1 网格情况Fig.1 Grid situation

图2 网格无关性验证Fig.2 Grid independence verification

流场计算采用商用CFD 软件CFX，在CFX 中控制方程采用了时均三维N-S方程，紊流模型使用标准k-ε模型。计算中给定了整个级的进、出口条件，将叶轮进口延长段处设置为总压进口条件，压力为标准大气压，温度设置为总温，值为300K，在蜗壳出口管道处设置为流量出口边界，转-静交界面设置为Frozen Rotor，固体壁面设置为不可渗透、无滑移及绝热壁面边界条件。

2 初始蜗壳方案流场分析

传统的蜗壳设计理论假定气流沿整个无叶扩压器圆周均匀流出，即通过蜗壳各截面上的流量从截面到蜗壳起始面之间所形成的方位角φ成正比：

由动量矩不变原理可得到蜗壳截面上气流速度沿径向分布规律，然后通过截面的流量求得截面大小和蜗壳外壁的直径，采用圆形对称截面蜗壳，初始设计模型如图3(b)所示，提取φ=270°截面处流线，可以看出由于过流通道突然扩张，气体径向流入蜗壳，受到蜗壳壁面约束速度降低，气体沿蜗壳壁面均匀分流，在蜗壳截面中心两侧形成低压区，气体在压力梯度的作用下，不断的从高压区域运动到低压区域，形成一对旋转方向相反的旋涡结构。从图3(d)压力云图可以看出，扩散段进口处的压力梯度大，压力分布不均匀，在蜗舌附近，静压变化不是很平缓，这些都会导致蜗壳性能的下降。对蜗壳性能影响比较大的结构参数主要是蜗壳截面形状、蜗壳截面面积和扩散段的扩散角θ，本文主要从这几个方面对蜗壳进行优化设计。

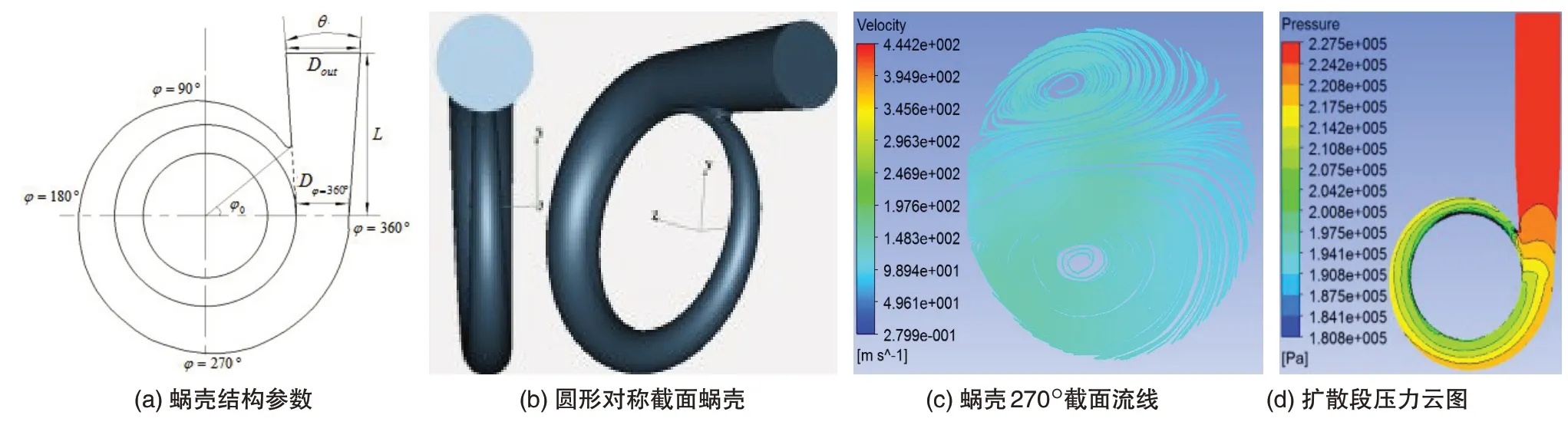
图3 初始蜗壳方案及流场Fig.3 Initial volute scheme and flow field

3 蜗壳气动方案优化设计

3.1 蜗壳截面形状对性能的影响

除了圆形对称截面，蜗壳常用的截面形式还有圆形不对称截面、梨形截面和梯形截面等，本节研究了后三者对蜗壳性能的影响，计算中采用的蜗壳截面面积沿周向角的变化规律基本相同，图4为不同截面形状的蜗壳三维模型。

图4 不同截面形状蜗壳Fig.4 Volutes with different cross-sectional shapes

由图5可知，圆形不对称截面蜗壳的效率与压比在四种截面形状的蜗壳中最高，其效率比圆形截面的效率高0.39%，而梨形和梯形性能都不如圆形不对称截面，性能上圆形不对称截面的蜗壳最优。

图6 为三种蜗壳在φ=270°周向角截面处的流线分布图，从图中可看出，三种蜗壳内都存在明显的旋涡流动，但与圆形对称截面蜗壳不同，三种蜗壳截面内只存在一个旋涡结构。

图6 周向角为270o截面流线分布Fig.6 Sectional streamline distribution at 270°circumferential angle

蜗壳内部不同的旋涡结构主要受到蜗壳进口径向速度和蜗壳截面形状的影响。在圆形不对称、梨形、梯形蜗壳中，气流切向壁面流入蜗壳，随着蜗壳周向角的增大，蜗壳径向速度增加，当下游径向速度更大的气体流入蜗壳，包裹住蜗壳内部已存在的气体，单旋涡结构自动形成；单旋涡的涡强度一般低于双旋涡，但梨形和梯形蜗壳内，靠近外壁面下部存在明显的低速区，蜗壳内损失反而比圆形截面蜗壳大，所以，圆形不对称蜗壳内气体流动情况最好。

从图7 中静压分布可以可看出，沿蜗壳径向方向，静压随着径向距离的增大而增大，并在蜗壳外壁面处静压达到较大值；气体在蜗壳内经过减速扩压，出口管路压力值达到最大。沿蜗壳壁面，圆形不对称蜗壳的静压梯度变化最小，静压分布最均匀，在蜗舌附近，圆形不对称蜗壳的静压变化相对也较平缓，说明在蜗壳内部采用不对称蜗壳气流分布更加均匀，流动性能更优。综合考虑，空压机蜗壳设计选取圆形不对称蜗壳。

图7 不同蜗壳截面形状静压分布Fig.7 Static pressure distribution of different volute cross-sectional shapes

3.2 蜗壳截面面积对性能的影响

采用一维方法来设计蜗壳型线的主要设计依据之一是蜗壳横截面上与截面垂直的分速度cu沿径向的分布符合动量矩守恒定律，即cu·r=常数，这与蜗壳内部的实际气体流动状况存在较大的差别。实际上，蜗壳进口流场在轴向和周向都是不均匀的，加之流体与蜗壳壁面之间的摩擦、压力梯度与离心力不平衡所造成的二次流及曲率对流动结构的影响，使得蜗壳内部的流场极为复杂，因此，研究蜗壳截面面积大小对整机性能影响是非常重要的。以不对称蜗壳为对象，在设计值附近选择不同截面积共6 种方案来研究蜗壳截面面积对性能的影响，图8为6个方案蜗壳截面面积变化情况。

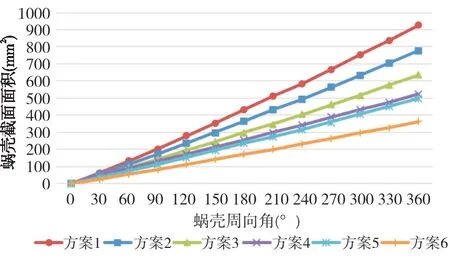
图8 不同方案截面面积随周向角变化Fig.8 The cross-sectional area of different schemes varies with the circumferential angle

图9为无叶蜗壳在不同截面面积下的计算结果，可以看出，整机的效率和压比随着蜗壳截面面积减小而先增大后减小。蜗壳截面面积较小时，整机的性能随面积变化剧烈，而过大的蜗壳截面面积性能也较差，方案5 的压比与效率在几种方案中最高。蜗壳截面面积与方案5 相近，整机的性能都较优，偏离较远时性能较差，蜗壳截面面积对整机的性能有显著影响。

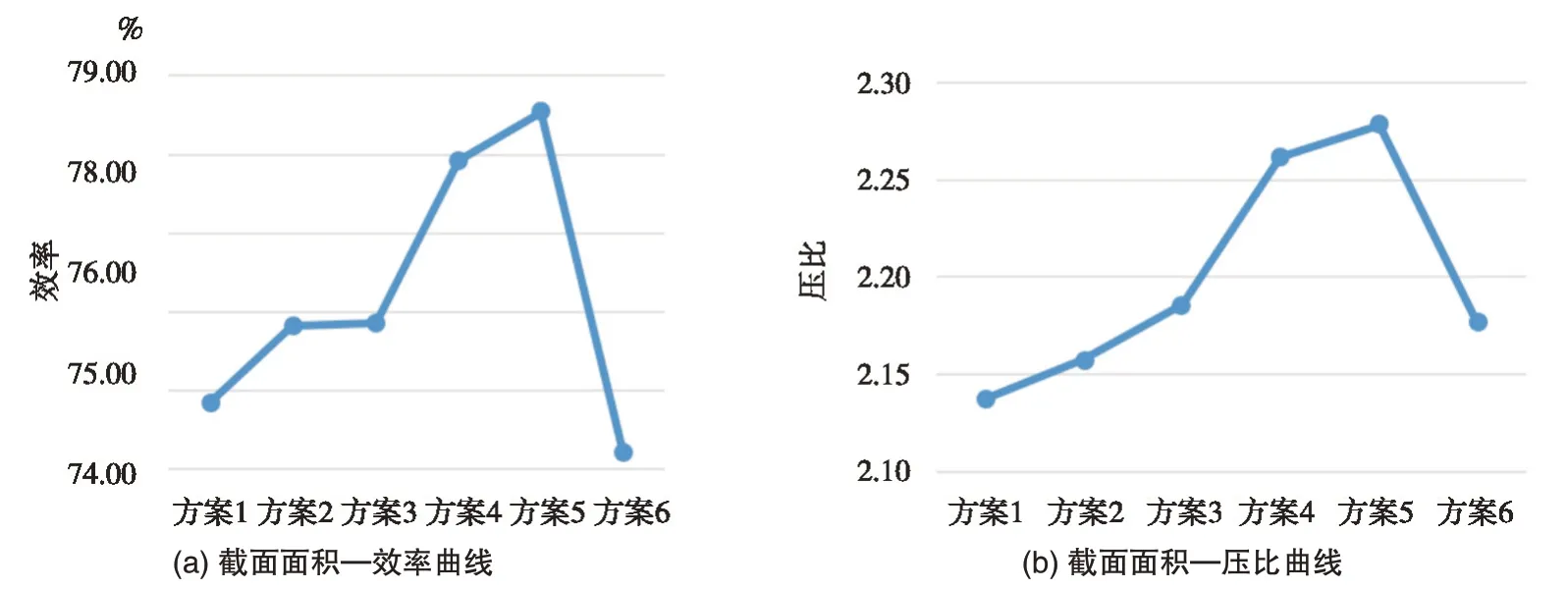
图9 蜗壳截面面积对性能影响Fig.9 Effect of volute cross-sectional area on performance

从图10蜗壳不同截面面积方案的流线分布中可以看出：方案2中，蜗壳截面面积较大时，由于面积的过度扩张，气流径向进入蜗壳内，使得扩压器内的流动极其不均匀，局部出现低速回流区；同时，较大的蜗壳截面面积让蜗壳壁面对气流的约束减弱，涡量较大，蜗壳室中心形成了单个大旋涡，造成整机的性能变差。随着蜗壳截面面积变小，扩压器内的流动逐渐变得均匀，蜗壳壁面对气体约束增加，气流旋转减弱，但方案4 出口管路出现了双旋涡结构，蜗壳截面面积稍小的方案5中，单旋涡结构损失较双旋涡小，所以性能优于方案4。当蜗壳截面面积过小时，蜗壳隔舌间隙过小，气流撞击蜗舌，使得扩压管路内形成大面积低速区，造成整机性能急剧下降。

图11 为蜗壳不同截面面积方案的静压分布云图，通过四种方案的比较可以看出，由于过大和过小的蜗壳截面面积使得蜗壳内流动混乱，所以压力分布不均匀且压力损失严重；而方案4和方案5的静压分布较为均匀，但方案5的蜗壳静压恢复能力比方案4强，蜗壳出口处的静压也大，综合比较，方案5 的整机性能比其余方案更优。

图11 不同截面面积方案压力分布Fig.11 Pressure distribution of different cross-sectional area schemes

图12 为蜗壳不同截面积方案的温度分布云图，通过四种方案的比较可以看出，整个蜗壳从进口到出口温度逐渐增加，这是因为从叶轮出来的气流具有很高的速度，且在蜗壳内部存在着分离损失、冲击损失和二次流损失，这些损失会转化为热量，从而导致气流在蜗壳内部的温度升高。温度越高说明蜗壳内部损失越大，效率也就越低。综合来看，方案5 在叶轮进口低温区域大，说明“转-静”部件动静干涉较小，压能转化效率较高，从出口也可以反映这一点，方案5 整个扩散段高温区域和温度梯度较小，所以性能较优。

图12 不同截面面积方案温度分布Fig.12 Temperature distribution of different crosssectional area schemes

3.3 扩压管扩张角对性能的影响

扩压管呈扩散状，能够降低蜗壳出口的气体速度，使气体一部分动能转变为压力能，减少蜗壳处的流动损失。本节研究扩压管扩张角对性能的影响，扩压管的进口可以看做是蜗壳φ=360°截面，出口为圆管，扩张角。

以无叶蜗壳方案5 为研究对象，分别研究了5°、6.4°、7.8°和9.2°四种不同扩张角方案，图13为不同扩张角的计算结果，可以看出，扩张角的大小对性能有一定的影响，其中方案2的效率最高。结合图14可以得到，增大扩张角能够增大出口处的静压比，但总压比会下降；随着扩张角的变大，静压恢复系数逐渐变大，而总压损失系数也相应变大，静压恢复能力增强的同时总压损失也增强。综合比较，选择效率最高的方案2为最佳方案。

图13 扩张角对性能影响Fig.13 Effect of expansion angle on performance

图14 扩张角对静压恢复和总压损失影响Fig.14 Influence of expansion angle on static pressure recovery and total pressure loss

由图15 可以看出，由于方案1 和方案2 的扩张角小，扩压管中没有明显的低速区域，没有分流损失，动压损失小。从图16的压力云图也可以看出这两个方案扩散段的压力较均匀，且压力梯度小。随着扩张角变大，括压度变大，方案3 和方案4 中出现了明显的低速区，产生了分离损失，性能下降。

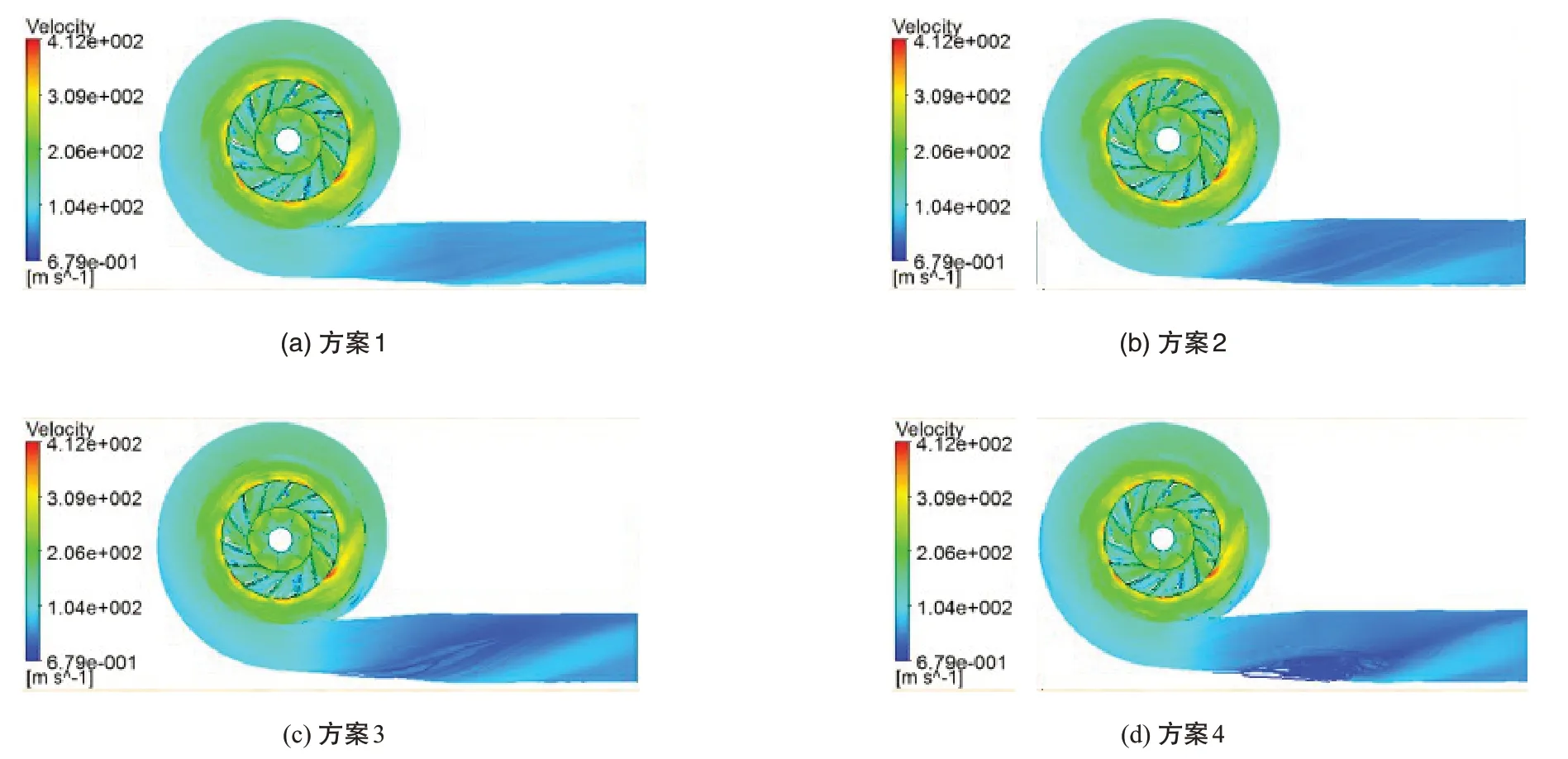
图15 不同扩张角方案流线分布Fig.15 Streamline distribution of different expansion angle schemes

图16 不同扩张角方案压力分布Fig.16 Pressure distribution of different expansion angle schemes

图17 为蜗壳不同扩张角方案的温度分布云图，对比方案1和方案2，较小的扩张角，扩散段会对气流约束变强，增加摩擦损失，根据前面分析这样会导致蜗壳扩散段温度的升高，所以方案1 在扩散段有一高温区域，所以综合来看，方案2性能最佳。

图17 不同扩张角方案温度分布Fig.17 Temperature distribution of different expansion angle schemes

通过以上优化，最终方案在设计点仿真级效率为78.76%，较原机仿真效率的77.8%提高了0.96%，气动性能改善明显。

4 试验验证

为验证计算结果的有效性，将空压机实测结果与模拟结果进行对比，搭建空压机空气性能测试台，对优化前后的空压机进行性能测试，测试原理如图18所示，限定空压机的转速，通过调节阀门来控制流量，流量值尽量与仿真边界所用流量相同，电脑采集温度、压力、功率等参数，如图19 所示，最后绘制空压机性能曲线，图20 是原机与优化后方案的测试结果。测试结果表明，优化后的蜗壳在全流量范围内压比和效率都比原机好，在设计点级效率提高0.95%，与仿真结果基本一致，说明了仿真方法和优化方法的正确性。

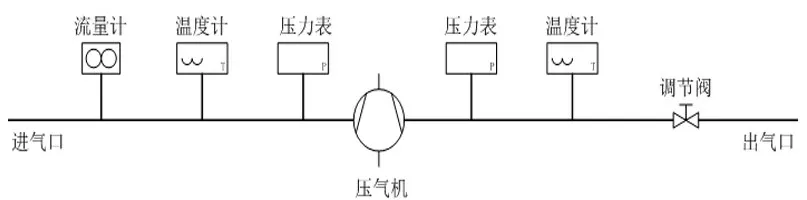
图18 空压机测试台原理图Fig.18 Schematic diagram of air compressor test bench

图19 数据采集界面Fig.19 Data collection interface

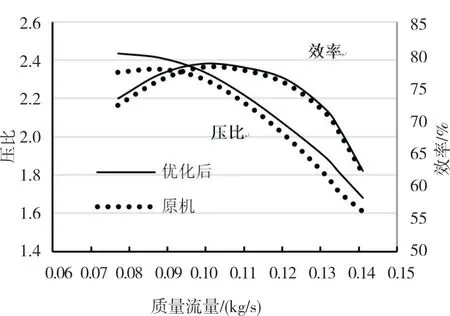
图20 空压机性能曲线Fig.20 Air compressor performance curve

5 结论

1）圆形不对称蜗壳流道内为单旋涡结构，流动损失小，并且蜗壳的静压变化相对也较平缓，分布较为均匀，流动性能更优；采用圆形不对称截面蜗壳在装配结构和流动性能上优于另外三种，因此，进行车用离心空压机蜗壳设计选取圆形不对称蜗壳。

2）蜗壳截面面积对性能的影响明显，过大的蜗壳截面面积使得扩压器内局部出现低速回流区，同时，蜗壳壁面对气流的约束减弱，涡量较大，性能较差；当蜗壳截面积过小时，蜗壳隔舌间隙过小，气流撞击隔舌，使得扩压管路内形成大面积低速区，造成整机性能急剧下降。最后确定截面Aφ=360°面积为496m2。

3）较小的扩压角会使得扩压管对气体约束增强，增加摩擦损失，而较大的扩张角会加大括压度，造成扩压管内分离损失；随着扩压角变大，蜗壳的静压恢复能力增强，但相应的总压损失会增加，最后确定扩散角为6.4°时级效率最优。

4）搭建空压机空气性能试验台，测试结果表明，优化后的蜗壳在全流量范围内压比和效率都比初始设计方案好，在设计点附近测试效率较原机提高0.95%，与仿真结果具有较好的一致性，该优化方法可以给后续蜗壳的设计提供指导。