动/静干涉对多级离心压缩机整体式静叶片特性影响研究
李春阳 冀春俊 杜凌萱 房骏翌,2
(1.大连理工大学能源与动力学院;2.辽宁福鞍燃气轮机有限公司)
0 引言
在国民经济的众多领域,如农业、动力和化工等均广泛使用压缩机输送气体,提高气体压力。然而,压缩机的主要级间部件,如扩压器、弯道和回流器中,能量均存在损失。本文研究的某多级离心压缩机的中间级,气体流经扩压器、弯道和回流器时,存在15.13%的流动损失[1]。因此,提高压缩机效率,节能降耗,是十分必要的。作者在离心压缩机级间静止部件的相关研究[2-6]基础上,已经提出一种新型的整体式静叶片设计方法,该叶片贯穿扩压器、弯道和回流器通道,对气流起到了良好的引导作用,提高了整级效率[1]。
然而,由于整体式静叶片安装位置和特殊的几何结构,需要着重考虑它和叶轮流场的相互干涉作用。动/静之间的区域指的是叶轮的尾缘与整体式静叶片前缘之间的部分,它们之间相互作用不仅影响压缩机性能,甚至引起叶轮震荡,影响机组安全运行。针对动/静叶干扰存在的复杂流场结构,Davis等[7]提出通道流场是时间平均流与动/静相互作用,自激流动和系统固有频率扰动下流场的叠加。很多学者把动静叶片交错排列简化为二维扩压叶栅,通过实验[8-9]和数值模拟[10-11]研究动/静干扰时流体流动的机理。刘赫[12]指出扩压器叶片前缘距叶轮叶片尾缘越近,非定常特性越明显。Shum YKP 等人[13]发现这种非定常相互作用主要影响叶轮叶尖的泄漏流,扩压器叶片上游的不稳定流动导致了更大的粘性损失。众多研究结果表明:叶片排之间干扰主要来自于尾迹和势流对叶片排的交替作用,这种交替作用也是叶片存在非定常气动负荷最主要的原因[14]。粘性尾迹直接影响下游的叶片,而压力场会对上下游叶片流场都产生扰动[15-17],势流参数场的影响范围大约与叶栅弦长具有相同的量级[18]。
叶轮机械数值模拟有定常计算和非定常计算两种方法。定常计算方法认为动/静叶之间的参数沿轴向均匀分布,只沿径向变化,因此忽略了尾迹对下一排叶片的影响;而非定常计算充分考虑到了转/静子之间的相对运动及叶片排的周向非均匀流动引起的非定常现象。由He 和Ning 于1998 年提出的非线性谐波法(NLH),它综合了定常计算速度快和非定常计算精度高的优点,节省了计算机资源。它将N-S方程由时域转化为频域,通过各个时间频域得到输运方程。马岩[18]等利用NLH对一台高速小尺寸的离心压缩机进行了非定常流动的数值模拟,研究结果表明,NLH可以有效地模拟动/静之间的非定常干涉现象。
本文分别应用定常和非定常方法研究动/静之间的径向间距对多级离心压缩机级间整体式静叶片的特性影响,定常计算分析其外特性规律,非定常计算观察动/静之间流场的相互干涉现象。
1 数学模型
本文的研究对象为多级离心压缩机的中间级,每一级由“叶轮+整体式静叶片”组成(如图1,研究的实体模型)。叶轮为闭式的(叶片数为13片),其后连接10个静叶片(见图2,整体式静叶片的三维造型),静叶片厚度15mm,计算域包括进口流道、叶轮、整体式静叶片及出口流道。
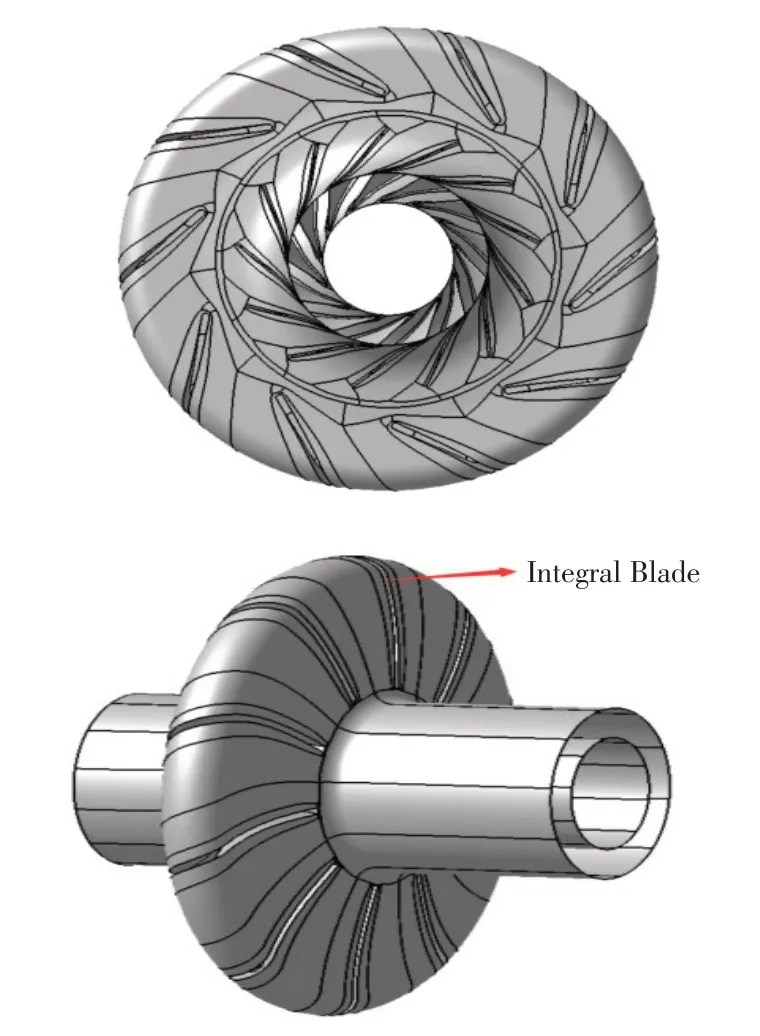
图1 模型整级三维造型[1]Fig.1 3D model of the compressor stage

图2 整体式静叶片三维造型[1]Fig.2 3D modeling of integrated blade
为了研究叶轮/静叶片之间的径向间距(R)对模型级性能的影响,本文根据静叶片的进口宽度是否变化,提供两种研究方式。
方案一:动/静之间收缩度不变的前提下,改变它们之间的径向距离。以R=45mm为例(见图3中红色点画线所示),动/静之间径向间距的增加会导致静叶片进口宽度变小(从bin=31.2mm 变为bin=27.3mm),整个叶片子午面的流道变窄。本文在原模型R=30mm的基础上,增加R=15mm和R=45mm两个间距,经过CFD软件求解流场后,它们的效率分别为73.34%和74.82%,压比分别为1.4 和1.429,和R=30mm 的模型级(效率和压比分别为78.28%和1.447),改进后的模型并没有达到优化的目的。因此,本文重点分析方案二中径向间距对静叶片性能的影响。
方案二:静叶片进口宽度不变,改变动/静之间的距离R。以R=45mm 为例(见图3 中蓝色虚线所示),动静之间径向间距的增加会导致叶轮出口至静叶片进口处流道的扩张,静叶片变短。

图3 动/静间距变化示意图Fig.3 Rotor/Stator radial spacing change
主要的几何参数见表1。

表1 模型级几何参数[1]Tab.1 Geometric parameters of the model
2 数值方法
利用AutoGrid5 模块对计算域进行离散,生成O4H型网格拓扑结构的结构化网格。关于网格的无关性验证见图4[1],单通道网格数目大于200 万时,级效率与压比随网格数变化不大,网格达到无关性要求。计算模型采用三层多重网格,全部网格的最小正交角>15°、最大长宽比<2000、最大延展比<5。考虑计算精度和时间成本,本文所有模型级单通道网格数均大于300 万。第一层壁面厚0.01mm,并对近壁面处的网格加密。近壁面第一层网格与壁面距离估算采用Blasius方程[19]:
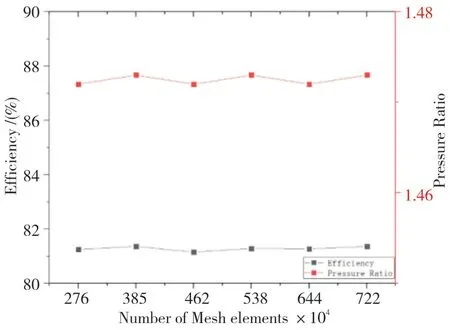
图4 网格无关性验证[1]Fig.4 Mesh independence
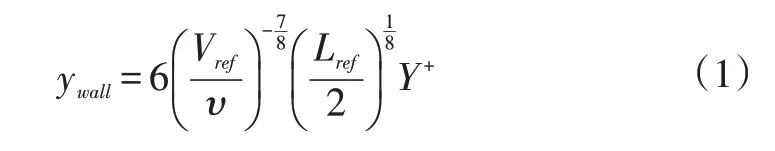
式中,Vref为特征速度,m/s;υ为运动粘度,m2/s;Lref为特征长度,m;Y+为无量纲参数。
应用Fine Turbo 模块对模型级流动分析,求解连续性方程、动量方程(三维雷诺平均N-S方程,湍流模型为S-A 方程)和能量方程。图5 为固体壁面的y+分布,满足S-A湍流模型对y+值(1-10)的要求。

图5 固体壁面y+值分布[1]Fig.5 The y+distribution on solid walls
流动介质为空气,粘性、可压缩。定常计算时转/静交界面为周向守恒型连接面,采用混合平面法处理。CFL 数为3,使用三重网格结合残差光顺方法加快收敛。气体轴向进气,总温和总压分别为101325Pa,288K,出口条件为7.6kg/s流量。绝热壁面,所有转动部件转速均为8129r/min。采用NLH法对模型进行非定常流动分析时,动/静交界面为一维无反射转/静子交接面。同时,以定常计算已经充分收敛的结果作为非定常计算的初场,以加快计算收敛的速度。
收敛标准为全局残差和各块中残差均下降三个量级以上;进出口质量流量相对误差小于0.5%,且流量不再发生变化。
3 结果分析
3.1 外特性分析
在本文中,叶轮叶片与整体式静叶片之间的相对径向间距用r表示(r=Rin/R2)。根据方案二提供的设计思想,令r=1.05~1.25。通过数值求解,得出动/静之间径向间距和模型级效率、压比的关系曲线,如图6 所示。从图中可以看出,在7.6kg/s的设计流量下,模型级的效率和压比随着径向间距的增加而增大。在r=1.25时,模型级在设计工况下有最大的效率和压比,分别为81.36%和1.473。通过和原有模型(效率78.28%,压比1.447)相比,效率提高3.08%,压比提高1.8%。模型r=1.25各流量下的效率和压比都明显优于模型r=1.05。

图6 模型级特性曲线Fig.6 Model level characteristic curve
将五组模型设计点处定常计算与非定常计算的结果展示于图7 中。从径向间距-效率的关系图中,可以看出在15mm的径向间距下,定常计算与非定常计算结果存在较大的差距;其余计算模型中,非定常计算的结果普遍优于定常计算的结果。在径向间距-压比的关系图中,也得到类似的情况。由于非定常计算考虑了转子/静子之间的相对运动和叶片排的周向非均匀流动现象,也说明了径向间距过小时,这种非定常现象加剧,随着径向间距的增加,两种计算方法的差距减小,动叶和静叶片之间的相互作用也减弱。
3.2 非定常流场分析
为了进一步分析不同径向间距下模型级内动/静之间的干涉现象,选择小间距、中等间距和大间距(r=1.05、1.15 和1.25)三组模型详细分析。图8~10 分别为三组模型在一个周期不同时刻的静压分布。
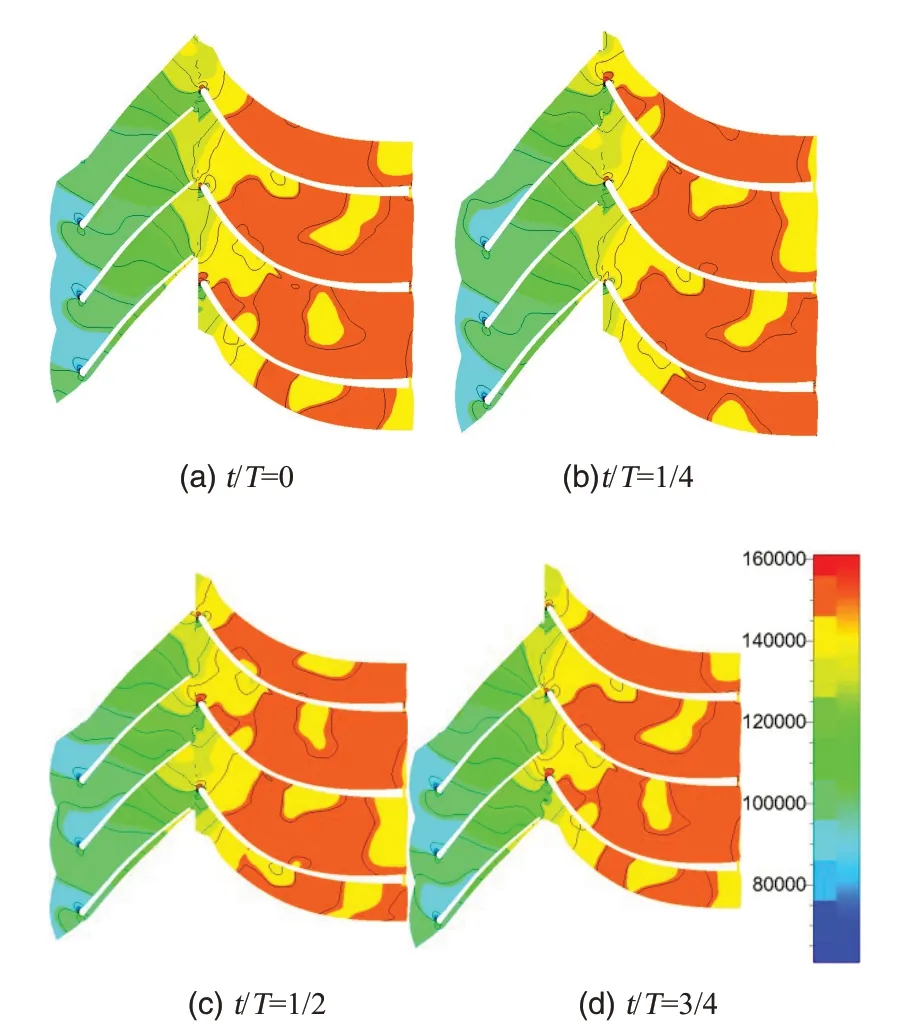
图8 模型r=1.05静压分布图Fig.8 Static pressure ditribution of model r=1.05
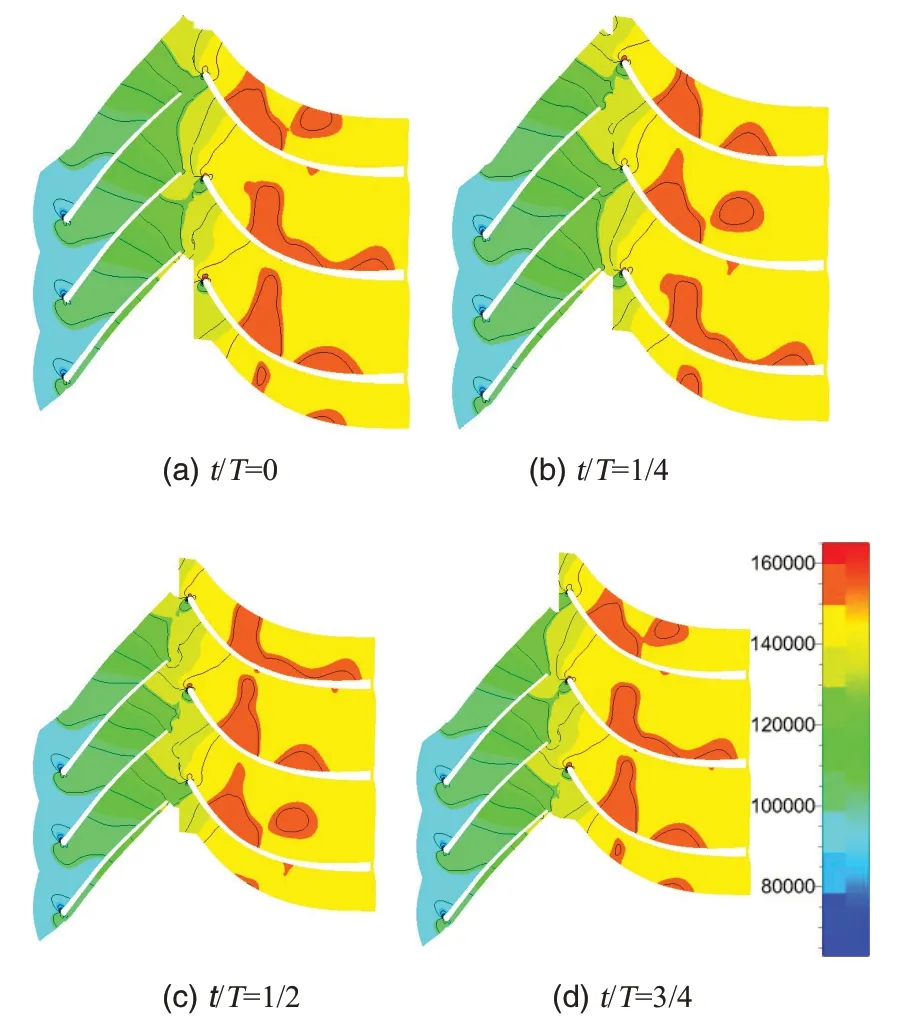
图9 模型r=1.15静压分布图Fig.9 Static pressure distribution of model r=1.15


图10 模型r=1.25静压分布图Fig.10 Static pressure distribution of model r=1.25
从图8~10可以看出气体流经动叶和静叶片时压力是一个逐渐升高的过程,随着时间的变化,三组模型级内的流场都呈现出非定常特性。模型r=1.05 级内的静压随时间的变化较大,尤其是叶轮出口至静叶片前缘之间的区域最为明显,此处压力等值线密集;而模型r=1.25 的静压随着时间变化不大,动/静之间的等压线稀疏。该结果同时也证明了动/静之间的距离越近,非定常特性越明显,它们之间的相互作用越强烈,影响强度随两个叶片之间距离的增大而减小。
为了进一步分析这种相互作用引起的流场变化,本文选择模型r=1.05进行级内速度矢量分析。图11为模型r=1.05一个周期不同时刻的速度矢量分布图,图12和图13分别为模型r=1.05静叶片前缘和尾缘流场的局部放大图。

图11 模型r=1.05一个周期不同时刻的绝对速度分布Fig.11 Velocity distribution of model r=1.05
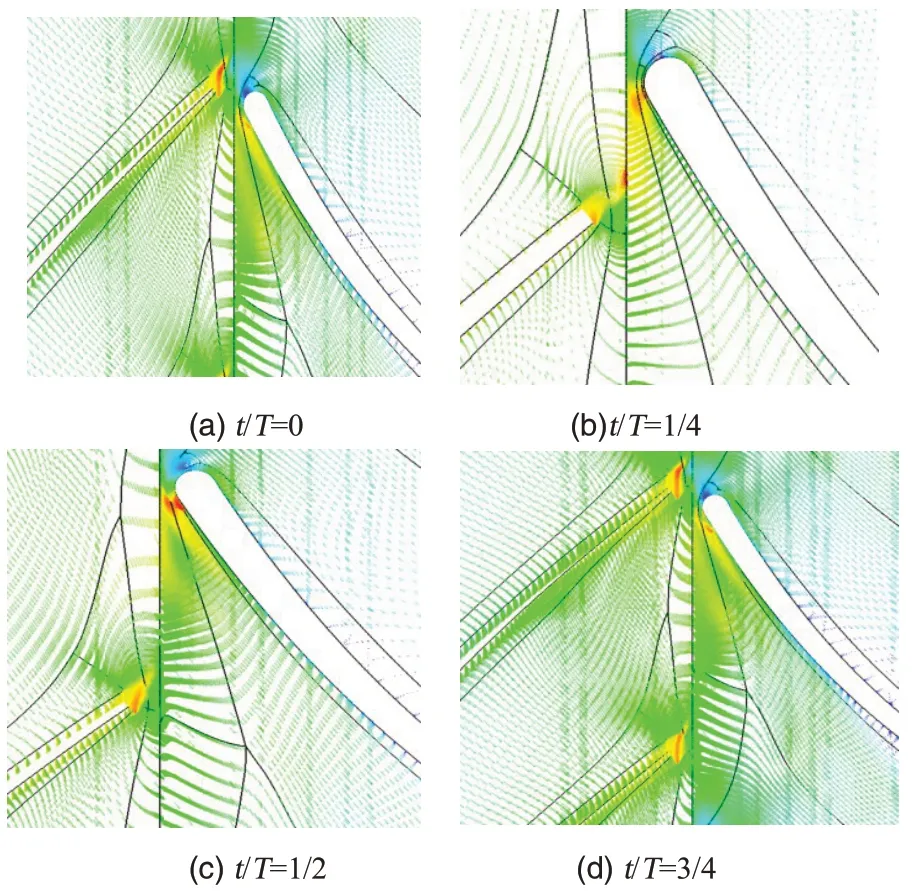
图12 模型r=1.05整体式静叶片前缘速度场局部放大图Fig.12 Velocity distribution of the integrated stationary blade leading edge of model r=1.05
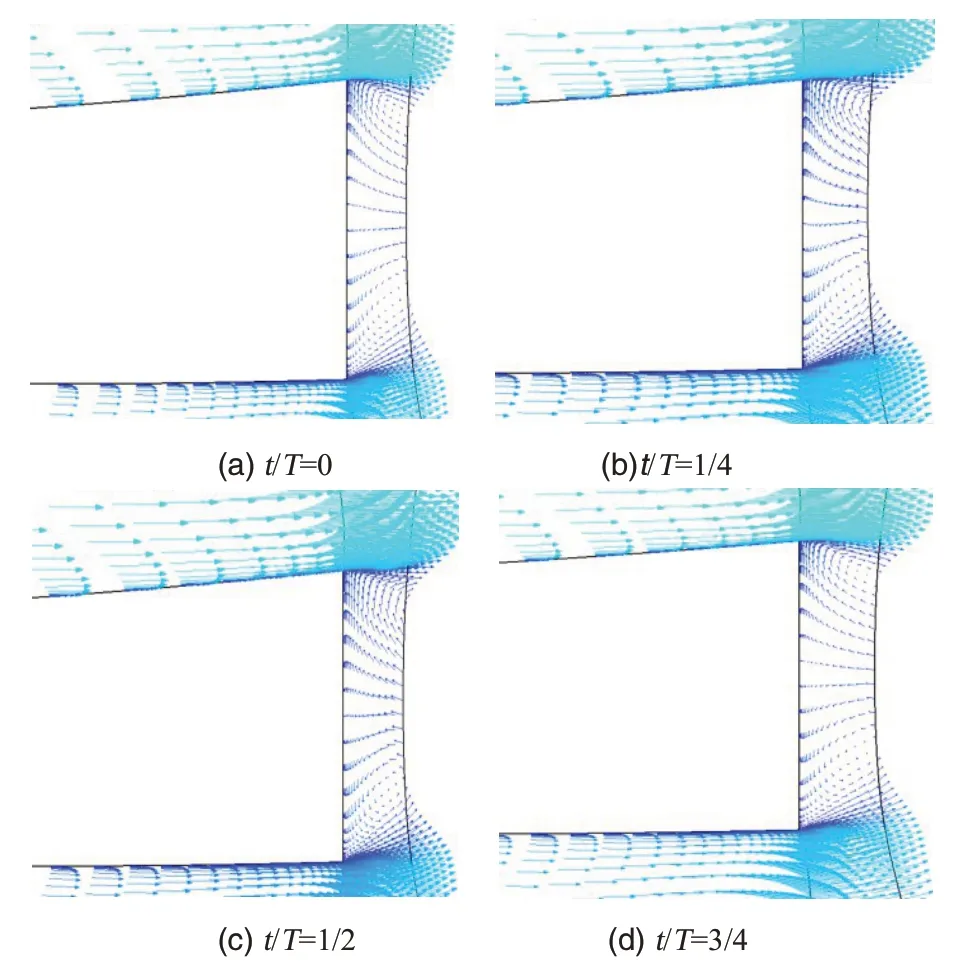
图13 模型r=1.05整体式静叶片尾缘速度场局部放大图Fig.13 Velocity distribution of the integrated stationary blade tailing edge of model r=1.05
结合图11~13 模型r=1.05 的速度矢量分布图可以看出,整体式静叶片前缘速度矢量比尾缘展现出更加明显的非定常特性和周期性。这是由于叶片前缘距叶轮叶片较近,动/静元件相互干涉较为强烈造成的。从图12 可以看出,叶轮叶片的周期运动引起其叶片尾迹的周期性变化,该尾迹会直接影响静叶片前缘的流场变化,引起进口气流角改变。
动/静叶之间的相对运动导致了叶片的不稳定载荷。由于流体的粘性,每个叶片都会产生一个压力场和尾流。叶轮叶片的粘性尾迹直接影响下游的叶片,而叶片的压力场在各阶段影响所有叶片,其他叶片反过来影响该叶片的压力场。影响强度随两个叶片之间距离的增大而减小。
3.3 叶轮叶片受力分析
叶轮和静叶片之间的相互作用可能会引起叶轮的振动甚至破坏。因此,考虑实际应用中的安全性,十分有必要研究这种相互作用对叶轮叶片产生的影响。如图14 和图15,分别表示五组模型叶轮叶片压力面和吸力面静压的平均值和静压差。
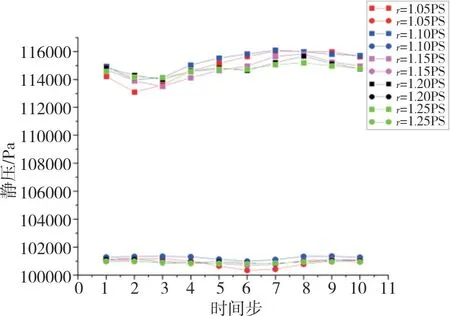
图14 叶轮叶片表面压力变化图Fig.14 Static pressure variation of impeller blade
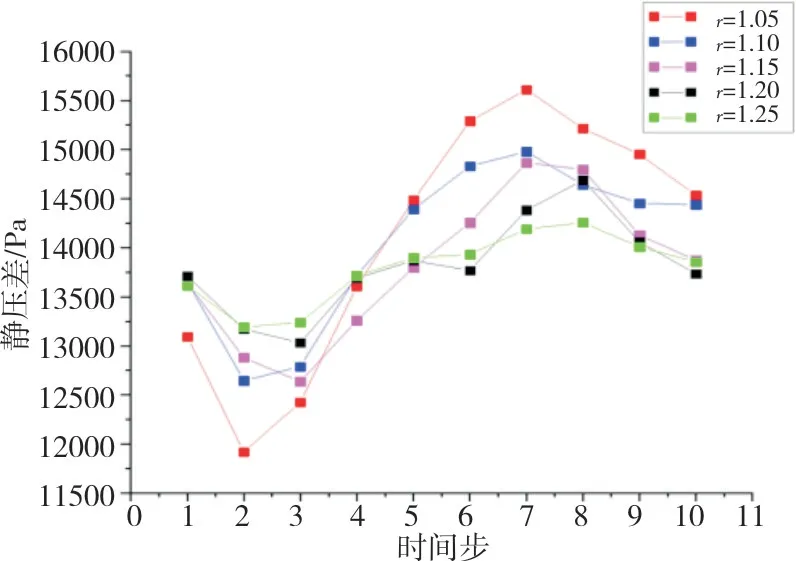
图15 叶轮叶片表面静压差图Fig.15 Static pressure difference of impeller blade
从图14 可见,五组模型一个周期不同时刻叶片的静压分布都存在周期性的变化。叶片吸力面所受的静压平均值较小,叶片压力面所受的平均静压较大。无论是压力面还是吸力面,模型r=1.05静压的变化幅度最大,模型r=1.25 静压的变化幅度最小。尤其是在吸力面,模型r=1.25 静压曲线基本呈直线趋势。结合图15可以看出,模型r=1.05压力面和吸力面的压差变化最为剧烈,模型r=1.25各时刻静压差随时间变化最小。
采用同样的方式对整体式静叶片的进口截面及出口截面的静压分布做研究,模型r=1.05~1.25 的静压曲线图见图16。从图中可以看出,模型r=1.05静叶片的进口和出口截面都表现出很强的非定常特性,尤其是进口截面,随着时间的变化,静压波动很大。模型r=1.25整体式静叶片进、出口截面的静压随时间变化波动很小,尤其是出口截面,基本不随时间变化。
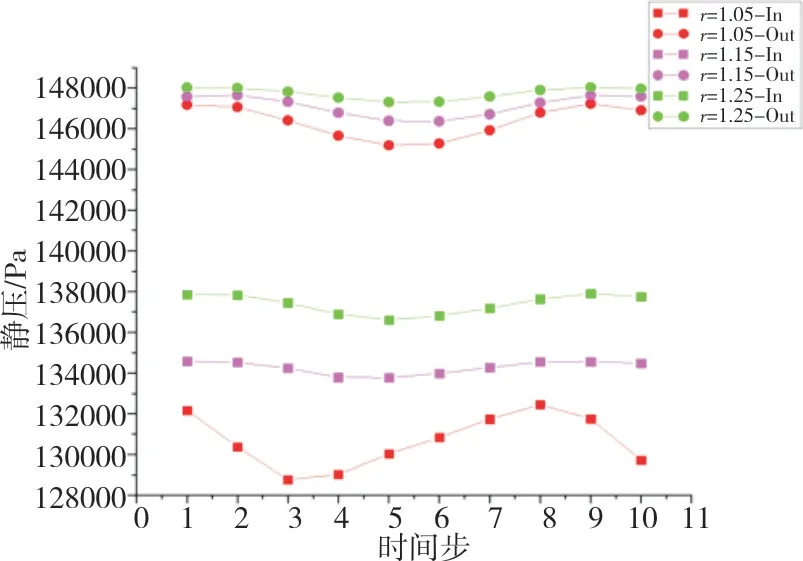
图16 整体式静叶片进/出口截面静压分布图Fig.16 Static pressure distribution of integrated stationary blade inlet and outlet section
结合图15 和图16 可以进一步发现,随着动叶和整体式静叶片之间距离的增加,静叶片引起压力场的变化对叶轮叶片影响逐渐减弱,静叶片的进口和出口截面的非定常特性也减弱,即二者的相互作用减弱。同时,模型r=1.25 叶轮叶片表面静压差变化均匀,也有利于叶轮的安全运行。
4 结论
本文分别应用定常和非定常方法研究动/静之间的相互干涉对多级离心压缩机内整体式静叶片的特性影响,定常计算分析外特性规律,非定常计算分析动/静之间的相互干涉现象。定常分析的结果表明,设计流量下,模型级的效率和压比随着径向间距的增加而增大。在径向间距R为75mm时,模型级在设计工况下有最大的效率和压比,分别为81.36%和1.473。通过和原有模型(效率78.28%,压比1.447)相比,效率提高3.08%,压比提高1.8%。模型r=1.25各流量下的效率和压比都明显优于模型r=1.05。通过比较不同模型的非定常现象,发现径向间距过小时,这种非定常作用加剧。整体式静叶片前缘速度矢量比尾缘展现出更加明显的非定常特性和周期性。随着径向间距的增加,动叶和静叶片之间的相互作用减弱;静叶片引起压力场的变化对叶轮叶片影响逐渐减弱,静叶片的进口和出口截面的非定常特性也减弱。同时,叶轮叶片表面静压差变化均匀,也有利于叶轮的安全运行。
通过本文的研究,不仅提高了模型级的效率,同时也分析了动/静干涉对整级流场的影响,消除了叶轮叶片振动的安全隐患,为离心压缩机整体式静叶片的实际应用提供了安全性保障。
- 风机技术的其它文章
- Study of Compressor Stall Margin Enhancement Using Tip Air Injection
- 车用空压机蜗壳优化设计研究
- 基于流线曲率法的轴流ORC膨胀机反设计*
- Reliable Operation of Turbomachinery Through Bearing Upgrades
- Reduction of Hot Oil Carry-over in High Speed Running Turbo Application Bearings
- Foil Bearing Technology for High Speed Single Stage Air Compressors for Fuel Cell Applications

