基于流线曲率法的轴流ORC膨胀机反设计*
薛彬彬 刘 艳 杨金广 李 志
(大连理工大学能源与动力工程学院)
0 引言
经过多年的发展,轴流涡轮的气动设计体系逐渐完善。自20世纪40年代以来涡轮气动设计体系可分为一维、二维、准三维、全三维和非定常气动设计等五个阶段[1]。一维设计方法主要利用涡轮基元级工作原理和简单径向平衡方程。1952 年吴仲华[2]先生首次将叶轮机械内部的三元流动分解为S1和S2两类二维流面内的流动,从而推动了以完全径向平衡方程为基础的涡轮二维设计方法的快速发展。随着计算机技术和CFD学科的进步,涡轮准三维设计方法逐渐在涡轮设计中发挥重要作用。所谓准三维方法,是指在进行通流计算时利用中心S2 流面和多个S1 流面进行交替迭代求解,从而得到涡轮内部流动的准三元解,一般S1流面的计算可以对各截面叶型进行优化设计,S2 流面的计算则能够得到涡轮气动参数的展向分布。目前准三维设计方法在工程应用中占据主要地位,国外一些先进的透平机械公司例如Rolls-Royce 和Pratt&Whitney 都在设计中采用了准三维迭代方法[3]。涡轮全三维设计方法的出现主要弥补了准三维方法对端壁流动效应计算的不足,同时可实现对激波的预测,目前全三维设计方法已经用于复杂涡轮叶片的优化设计,用于研究叶片不同径向积叠方式和弯扭效应对涡轮性能的影响。涡轮非定常设计体系则将气动设计体系和非定常流动因素进行有机结合,从而实现气固热耦合的涡轮一体化优化设计[3]。
近年来,为实现节能减排和保护生态环境,以膨胀机作为核心动力部件[4-5]的有机朗肯循环(Organic Rankine Cycle,ORC)系统在工业余热回收方面正发展为一种应用前景广泛的节能技术。由于ORC膨胀机采用有机工质,因此以往的理想气体计算方式在设计过程中并不适用,为了满足膨胀机的设计需要,本文使用Fortran95 语言[6]开发了一套适用于真实气体的轴流涡轮二维反设计程序,该程序在S2 流面内对涡轮进行设计,采用流线曲率法[7-8]求解完全径向平衡方程[9-10],同时考虑了真实气体热物性随热力状态的变化,因此除了ORC类膨胀机,也能进行多级轴流涡轮的设计应用。
1 设计方法
1.1 控制方程
图1 为叶轮机械中S1 与S2 两类相对流面示意图,在S2流面上进行反设计的目的是求解气动参数沿叶片展向的分布,从而选择合适的叶片扭曲规律,使级载荷和效率保持较高的状态。假设叶排间隙内流动为定常、绝热、无粘的,且在周向为轴对称[11],计算站设置在叶片前尾缘处且不考虑叶片力的影响。如图2所示,则流体质点沿准正交计算站q方向的运动方程可以表示为

图1 S1/S2流面示意图Fig.1 Schematic diagram of S1/S2 flow surface
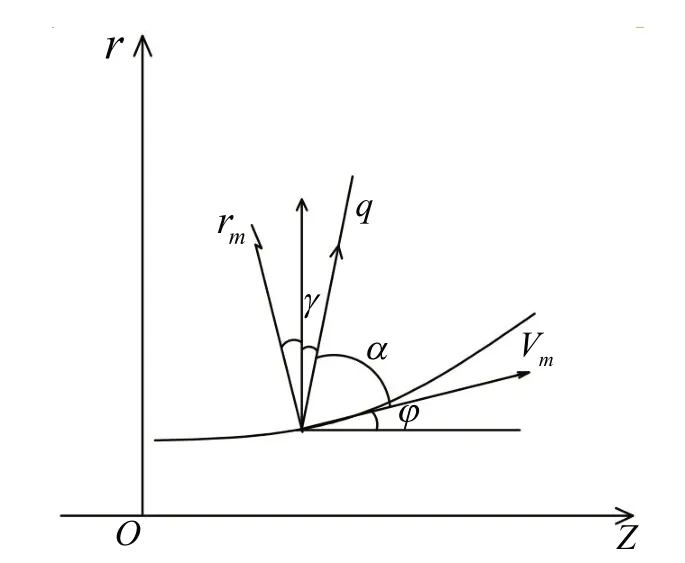
图2 子午面内运动分析示意图Fig.2 Schematic diagram of S2 flow surface motion analysis
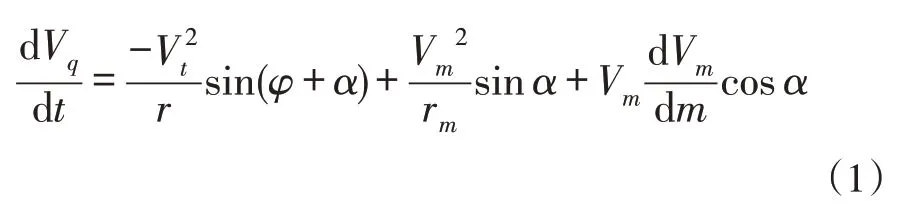
其中,rm为流线曲率半径。
将热力学第一定律沿准正交方向q求导得到:
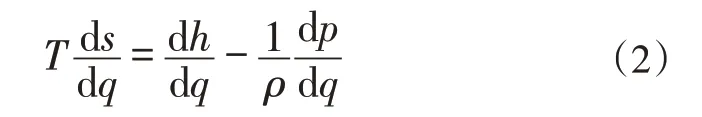
能量方程:

联立式(1)~(3),得到绝对坐标系下准正交方向子午速度分布的控制方程为
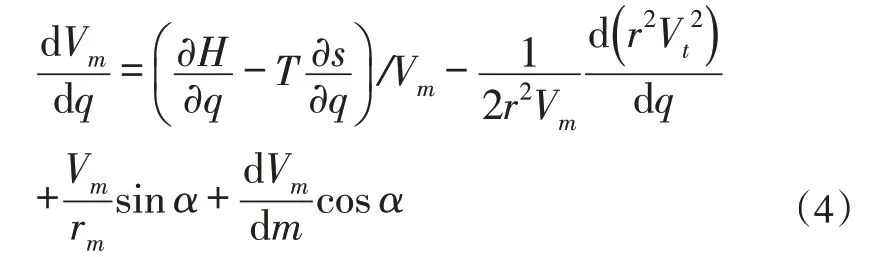
其中,Vm表示子午速度;q为准正交方向;H表示气体总焓;T表示静温;S代表气体熵;Vt为切向速度;α为子午速度与q方向的夹角;m表示子午流线方向。
由于在整个展向方向上气体的通流能力是不同的,则通过任意计算站的质量流量为:
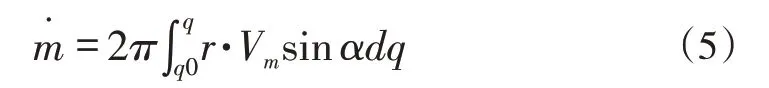
采用二阶精度的有限差分方法对方程(4)进行离散求解,从而求出子午速度Vm沿准正交计算站方向的分布,之后根据方程(5)的计算流量与设计流量之间的关系对流线位置进行逐步调整,直到满足指定的流量公差和流线位移公差。
1.2 真实气体
为实现对ORC 膨胀机的设计,反设计程序在编写时考虑了流体可压缩性和真实气体比热随温度的变化。为实现物性的准确计算,本文在求解过程中通过调用NIST Refprop[12]进行物性查询,工质的熵和焓通过调用自定义物性函数进行计算,
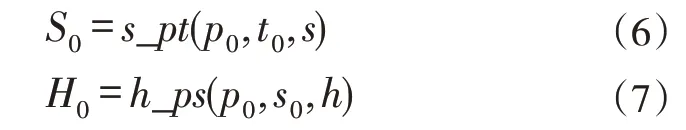
由于在求解过程中涉及大量迭代,为提高计算效率,程序通过外部接口调用NIST Refprop生成相应的物性表格,之后使用双线性插值法[13]对物性表格进行调用。物性表格范围根据涡轮整个运行工况范围内的压力和温度范围确定,本文采用基于压力和熵生成的R245fa 物性表格大小为500×500,精度为10-6,调用物性表格的计算方法在保证准确性的同时节省了大量时间,从而极大的提高了计算效率。
1.3 收敛因子
图3为程序逻辑简图,可以看到程序共包含内外两层迭代,其中内层迭代用来求解主控制方程,从而得到子午速度的展向分布,外层迭代则用来逐渐调整流线的径向位置,从而满足各径向流管内的流量守恒条件,当内外两层迭代都满足指定的收敛精度后,程序求解结束。为避免迭代中因流线位置调整幅度过大而导致发散,程序引入了相应的流线阻尼因子,从而在提高计算速度的同时保证程序具有良好的收敛稳定性。
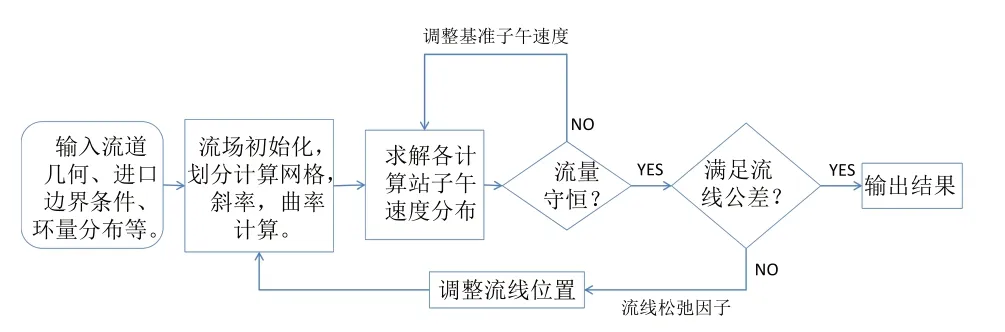
图3 程序逻辑简图Fig.3 Schematic diagram of program logic
一般情况下,流场初始化得到的子午速度分布与最终的子午速度分布相差较大,因此在迭代求解过程中需要不断对基准流线上的子午速度进行调整,从而满足各计算站上的流量守恒条件。本文根据当前计算站流量与设计流量之间的关系来调整基准流线上的子午速度,在更新子午速度分布过程中,若当前计算站流量偏小,则采用式(8)调整基准流线上的子午速度:

若当前计算站的计算流量偏大,则用式(9)进行调整:
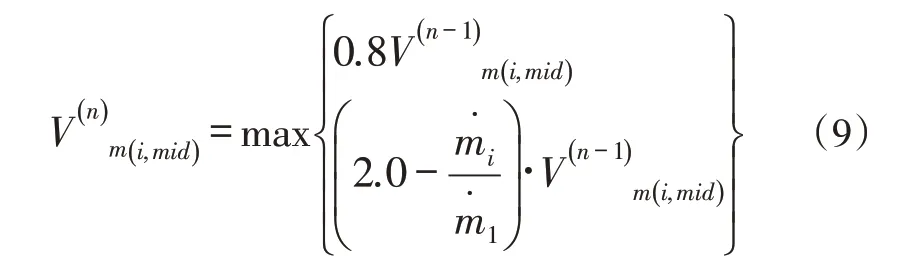
通过(8)、(9)两式可以根据当前计算站流量与设计流量之间的偏差,合理调整基准流线上的子午速度大小。此外,在调整径向流线位置时,采用Wilkinson[14]提出的松弛因子计算方法,在指定径向位置上
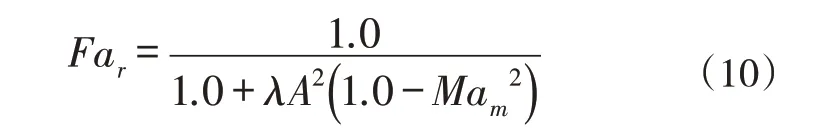
其中,Far表示当前计算站所在流线上的松弛因子;λ为常数;通常取0.2;A代表计算网格点处的网格长宽比;Mam代表所在流管中的平均子午马赫数。若进行第n-1 步迭代时,第j条流线经上一次调整后的径向位置为,则第n步迭代时该流线径向位置被调整为:
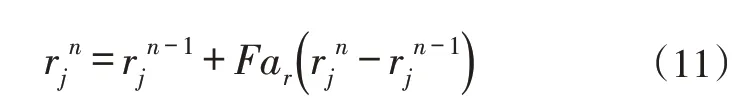
1.4 损失模型
为了对不同设计方案下涡轮性能的优劣进行评估,在设计过程中需要引入相应的损失模型。在轴流涡轮中,根据损失产生部位的不同,可将损失分为叶型损失、二次流损失和叶顶间隙损失[15],本文的反设计程序中关于损失的计算分为采用损失模型和指定总压损失系数两种方式。设计者可以通过指定各条流线上的总压损失系数进行通流计算,这些损失系数根据设计者的经验或者从实验结果中获得,考虑到实际流动的三维效应,一般指定的压力损失系数可以遵循中间小两端大的分布趋势。为提高设计过程中涡轮性能预测的准确性,本文的S2 反设计程序采用了较为准确的AM&DC[15-16]损失模型,该模型在传统的Ainley&Mathieson模型基础上考虑了雷诺数和马赫数对流动的影响,并改进了叶顶间隙损失的计算方法。需要指出的是AM&DC模型未考虑流体的可压缩性,因此在跨声速区的性能预测上存在误差,并且其认为雷诺数只影响叶型损失和二次流损失的大小[17]。
基于以上介绍的反设计程序,在得到气流角的展向分布后,利用课题组内基于Pritchard 11参数法[18]开发的二维参数化造型程序进行涡轮叶片造型,该参数化造型方法与优化算法相结合,通过调用Mises 求解器[19]对叶片性能进行评估,程序输入参数包括叶片进出口气流角、出口马赫数、叶片稠度等,程序能自动优化叶片最大厚度位置、尾缘厚度、前尾缘楔角等几何参数,从而得到高效气动性能的叶型。
图4为该造型程序得到的二维叶型示意图,叶型共分为前缘、压力面和吸力面三段曲线,其中前缘为一段圆弧,吸力面和压力面分别为5 阶和4 阶贝塞尔曲线,根据叶片扭转程度选择所需要的截面数,之后根据一定的叶片集叠规律便可以得到三维叶型。对于自由涡扭曲规律的叶片来说,一般只需要叶根、叶中和叶顶共三个截面的叶型,为了保持一致性,本文在进行叶片设计时转静子叶片均采用重心集叠方式进行三维叶片生成。

图4 二维叶型设计图Fig.4 Two-dimensional blade profile design drawing
2 数值计算方法
为验证反设计程序的有效性,本文采用CFD 数值模拟预测设计涡轮的性能。数值计算采用NUMECA的FINE/Turbo软件包求解定常三维雷诺平均N-S方程[20],网格划分采用AutoGrid5 生成O4H 自适应结构化网格,动叶顶部间隙内采用蝶型网格,并对叶片前尾缘网格进行了加密处理,计算总网格数均经过网格无关性验证。
涡轮进口边界条件为指定总温总压和进口气流角分布,进口湍流度取<1%,计算湍流模型选择Spalart-Allmaras[21]一方程模型,近壁面y+值约为3,出口给定中径处静压值,并采用径向平衡条件。
3 程序验证
3.1 涡轮设计
为提高二维程序的可靠性,本文以某单级轴流涡轮[22]进行了反设计验证。该涡轮工质为理想空气,进口总温360.0K,总压187.54kPa,出口静压108.0kPa,转速13000rpm。
本文根据现有结构和边界条件,对原涡轮展开了数值模拟计算,之后根据计算结果,提取了涡轮进口展向的总温、总压分布以及转静子叶片的出口环量分布,并以此作为二维程序的输入参数。
实际流动中,由于粘性边界层以及各种二次流的相互作用,在近端壁处环量提取值与设计值之间往往存在较大偏差,因此本文对涡轮展向5%~95%叶高的环量分布进行线性外插值得到整个展向的环量分布,之后利用二维反设计程序对涡轮进行了通流计算,表1为重新设计后的结果与CFD结果的对比,为便于比较,表中一维及二维设计所需参数均从CFD数值模拟结果中提取。

表1 涡轮总体性能Tab.1 Overall turbine performance
从表1可以看出,二维反设计程序计算得到的涡轮总体性能参数与CFD 结果存在一定的偏差,这主要由以下两方面的原因造成的。一方面是由于从CFD结果中提取的环量分布不够准确,实际流动中,由于粘性损失以及二次流的影响,叶片近端壁区域的环量分布往往与设计环量偏差较大;另一方面则是由于反设计程序所采用的设计点损失模型存在一定的误差。在计算过程中子午速度是通过迭代求解的,因此局部环量分布规律会影响整个计算站的子午速度分布。相比于一维设计,二维通流设计的优势在于能够获得涡轮参数的展向分布,同时考虑了子午流线斜率曲率变化对流动的影响。通过分析表1,二维设计结果与实际流动情况比较吻合,这说明本文的二维设计方法虽然忽略了一些流动现象,但是却能够较好的抓住涡轮内部流动的本质,从而获得与三维实际流动更加接近的结果。
图5为程序和CFD结果的流场静压云图,整体上计算得到的静压分布规律与三维数值模拟结果比较相符。

图5 程序和CFD流场静压分布云图Fig.5 Static pressure contours of the program and CFD
图6 为转静子叶片出口气流马赫数沿叶高的分布情况,可以看出静叶栅出口整个叶高范围内程序计算结果与CFD 吻合良好,动叶出口根部区域相对马赫数比CFD 结果偏大,这可能是由于实际流动中动叶根部区域的损失较大,造成静温度的升高导致的。动叶顶部近壁面区域内,由于叶顶泄漏涡和端壁通道涡的共同作用,流动情况比较复杂,导致计算马赫数和CFD结果存在一定偏差,本文的S2 反设计程序由于不考虑粘性的当地影响,因此在这些高损失区域内参数的计算结果与CFD 结果相比误差较大,这点从控制方程中没有二阶粘性力项也容易看出。

图6 叶片出口马赫数展向分布图Fig.6 Spanwise distribution of Mach number at blade outlet
4 程序应用
4.1 膨胀机设计
本文对某多级ORC 膨胀机进行了设计,以此来验证该反设计程序对真实工质涡轮的设计能力,具体设计要求如表2所示。
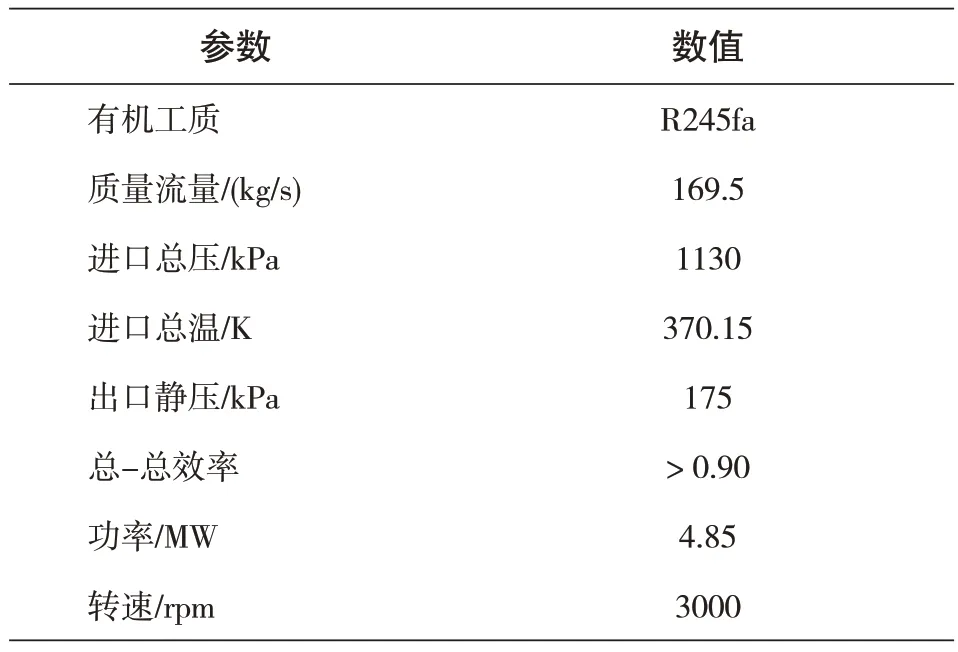
表2 R245fa轴流膨胀机设计参数Tab.2 Design parameters of R245fa axial flow expander
在实际应用中,涡轮级数一般随功率和流量增加而增大,同时合理的级数也能保证涡轮较高的流动效率以及节约制造成本。根据设计要求,综合考虑各级压比、尺寸等,本文最终确定的膨胀机为两级方案。
该膨胀机工质为有机工质R245fa,设计点工况总静压比约为6.46,为了避免涡轮局部子午扩张角过大,在满足设计要求的情况下,采用了等中径的流道形式。第一级喷嘴采用全周配气方式,气流方向为轴向,估计涡轮进口马赫数为0.29,得到涡轮进口叶高为35mm,中径尺寸约为770mm,涡轮各级环量分布如图7所示。
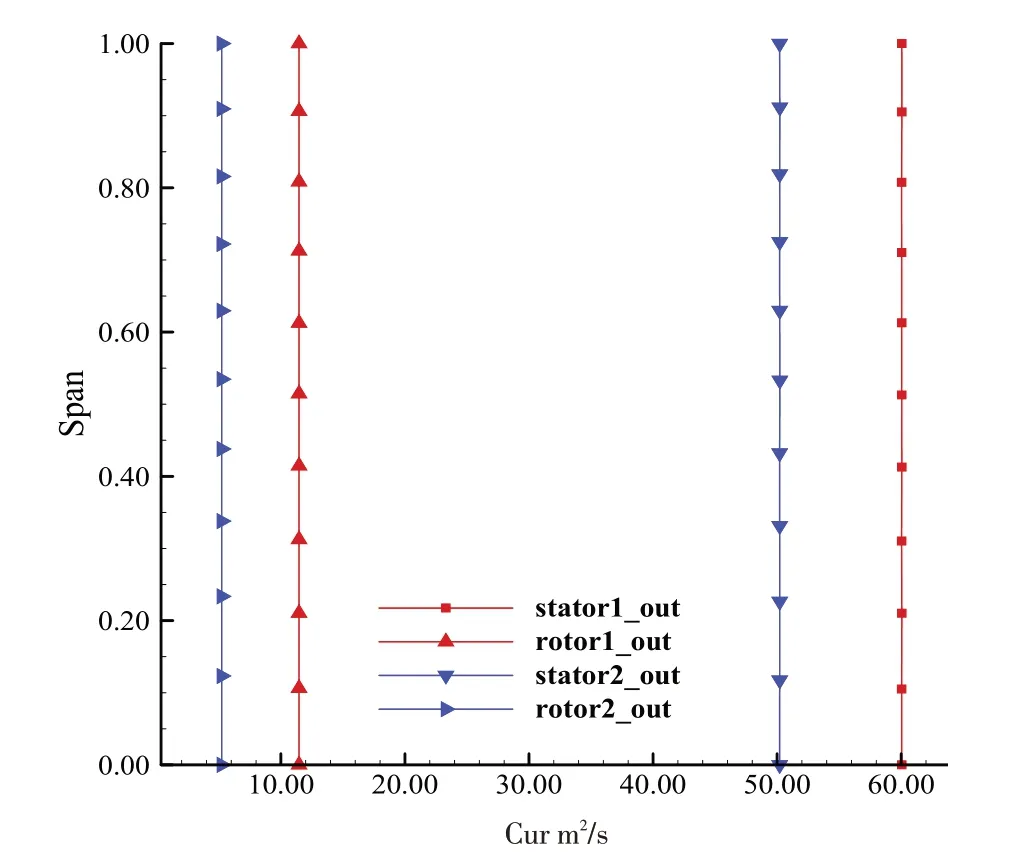
图7 叶片环量分布Fig.7 Circulation distribution of blades
4.2 设计结果
根据以上设计条件,得到涡轮二维设计总体性能参数如表3所示。
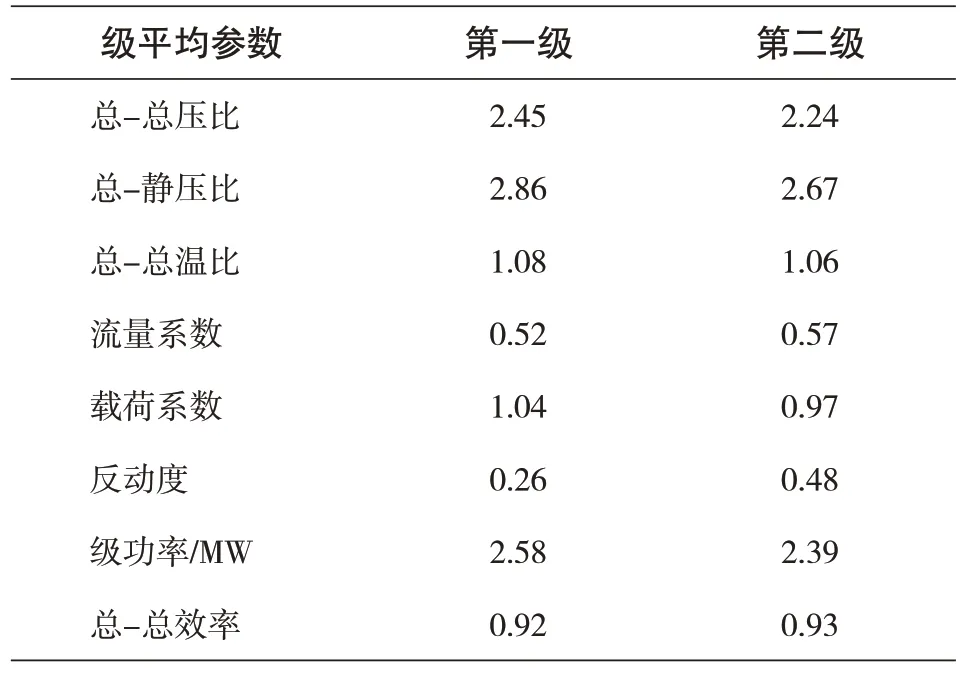
表3 设计结果Tab.3 Design results
4.3 结果分析
根据二维计算结果得到的叶片进出口气流角分布,进行叶片三维造型,并采用三维CFD数值模拟分析膨胀机性能。两级膨胀机计算网格如图8所示,除第一级静叶外,膨胀机子午流道均匀扩张,这是由于在设计过程中不希望轴向速度有过大变化,同时均匀扩张的流道有助于减少壁角区域的涡流。表4 给出了膨胀机二维和三维计算结果的总体性能参数。

图8 计算网格Fig.8 Computing grid
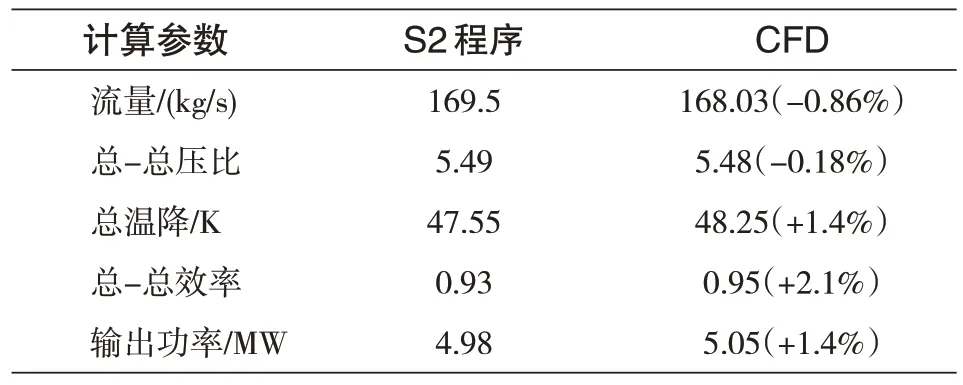
表4 总体性能参数Tab.4 Overall performance parameters
数值模拟结果显示,涡轮进口流量比设计值低了约0.86%,功率和效率都满足设计要求,二维反设计效率要低于三维CFD 计算结果,这是由于二维计算中过高的损失估计造成的。
图9为S1流面内流场马赫数云图,由于采用了自由涡设计方案,前两级静叶根部区域载荷较大,在叶片吸力面出口附近均存在部分超音速流动,从叶片表面流线来看,各区域的流动情况较好,除叶片前尾缘外无明显的流动分离现象。

图9 相对马赫数分布图Fig.9 Relative Mach number distribution
程序计算结果与CFD结果的叶片出口马赫数展向分布如图10 所示,通过对比可以看出,除端壁边界层外,整个叶高方向上反设计与CFD 结果得到的叶片出口马赫数分布规律基本一致。图10(a)显示第一级静叶出口马赫数比CFD 结果整体偏小,但都处于超音速流动状态,此时在静叶出口区域存在激波损失,由于落后角的存在,实际出口气流方向向轴向偏转,而在通流反设计计算中采用的是涡轮设计点损失模型,并没有考虑到落后角的影响,这是造成这部分偏差的主要原因。图10(b)为第二级转静子叶片出口马赫数分布图,程序计算马赫数CFD计算结果在整个叶高范围内的变化趋势是相同的,但同样在数值上存在一定偏差,第二级计算结果除了损失计算方法带来的误差外,还受到第一级出口计算站参数的影响,因此第二级的流动状态不如第一级。在近端壁区域内程序计算结果与CFD数值模拟结果吻合较差,这是由于透平机械内部的真实流动具有强烈的三维特性,特别是在端壁角区以及叶片的前尾缘,由于流体粘性作用,多种附面层相互堆积,存在着各种分离流动形成的二次流,这部分低能流体与叶栅通道内的主流形成相互掺混,造成损失,从而导致计算结果出现偏差。

图10 叶片出口马赫数分布对比图Fig.10 Comparison diagram of Mach number distribution at blade outlet
图11 和图12 为叶片表面的极限流线分布图,可以看出在叶片近端壁区域由于粘性边界层的影响,叶片表面的流场均匀性遭到破坏,产生二次流损失。在叶片吸力面上下端壁可以明显观察到分离流动在叶片表面的再附着现象,这是端壁通道涡以及叶片前缘分离涡向下游发展的结果。动叶顶部由于叶顶间隙的影响,泄漏涡与通道分离涡等相互叠加使流动状况恶化,部分压力面流线越过动叶顶部向吸力面流动,从而造成掺混损失。

图11 叶片压力面极限流线Fig.11 Limit streamline of blade pressure surface

图12 叶片吸力面极限流线Fig.12 Limit streamline of blade suction surface
5 结论
本文利用自主开发的S2 反设计程序对不同工质、不同级数的轴流涡轮进行了设计验证,使用与优化算法和二维叶栅求解器(Mises)相结合的叶型参数化平台进行了叶片造型,并通过NUMECA 流体仿真软件对涡轮进行了数值模拟计算,经过结果对比分析,表明了该轴流涡轮S2反设计程序具有一定的应用价值。本文结论如下:
1)本文利用流线曲率法开发了一套适用于真实气体轴流涡轮的二维反设计程序,该程序在中心S2 流面上进行通流计算,所需设计参数只包括涡轮通流几何和各级叶片环量分布。相比矩阵通流法[23](流函数法),该方法物理意义明确,编程简单,并且在计算过程中占用更少的计算机内存。
2)本文采用的二维反设计方法既适用于亚音速涡轮设计,又可用于跨音速涡轮设计,由于程序中采用了简单有效的流线调整阻尼因子和基准流线速度调整方法,不仅使程序具有较好的收敛性和计算稳定性,同时在指定的精度要求下,程序收敛速度快,计算准确度高。
3)由于程序嵌入了真实工质的物性计算功能,求解时通过双线性插值法查询物性参数,从而能够对任意工质的轴流涡轮进行设计。
4)通过涡轮设计实例表明,该程序的计算误差主要存在于对各项损失的预测上,程序中所采用的AM&DC损失模型还需要做进一步的修正,特别是进行超音速涡轮的设计时,由于未考虑到激波带来的附加损失,计算结果与实际流动结果将产生一定的偏差。为进一步提高反设计程序的精度与可靠性,改进损失模型将会是后续的工作内容。
- 风机技术的其它文章
- Study of Compressor Stall Margin Enhancement Using Tip Air Injection
- 车用空压机蜗壳优化设计研究
- 动/静干涉对多级离心压缩机整体式静叶片特性影响研究
- Reliable Operation of Turbomachinery Through Bearing Upgrades
- Reduction of Hot Oil Carry-over in High Speed Running Turbo Application Bearings
- Foil Bearing Technology for High Speed Single Stage Air Compressors for Fuel Cell Applications

