车用涡轮增压器压气机变海拔性能多目标优化设计

刘 刚，汪陈芳，杨震寰，张扬军

（1.清华大学汽车工程系汽车安全与节能国家重点实验室，北京 100084；2.军事交通学院军用车辆系，天津 300161；3.中国北方发动机研究所（天津），天津 300400）

我国国土面积中海拔2 000m以上的高原占33%，主要分布在西南和西北部地区。其中，青藏高原总面积约为240万km2，平均海拔4 000m以上，是世界上平均海拔最高的高原，有世界屋脊之称［1］。近年来，随着高原地区经济不断发展，内地与高原地区的交通运输联系更加紧密，汽车和火车作为往来于平原和高原地区的物资运输的重要工具，其变海拔性能显得尤为重要。

从平原到高原，海拔高度变化剧烈。以青藏公路为例［2］，从西宁（海拔2 200m）出发，沿途需要经过海拔5 100m的唐古拉山口才能到达拉萨（海拔3 800m）。通常，将按平原大气条件设计和匹配的涡轮增压发动机安装到车辆上向高原地区行驶时，会出现燃烧恶化、输出功率下降、燃油消耗率升高现象，可靠性也受到影响［3］。这是因为随着海拔不断升高，大气压力不断下降，相同转速和工况下，发动机的进气量不断减少，从而导致增压器与发动机匹配良好的联合运行线发生偏移，压气机的效率不断降低，流量不断减小，且喘振、超速的趋势增加。

因此，针对高原应用的实际情况，在尽量不改变原机外形和结构的前提下，对增压器进行变海拔性能优化设计是提高车用发动机变海拔工作性能的重要技术手段。基于这个目的，本研究参考航空领域的基于多目标优化方法的机翼变工况优化设计方法［4－7］，提出了针对车用涡轮增压器压气机变海拔性能的优化设计方法，对高原型发动机的工程开发具有一定的参考意义。

1 压气机多目标优化方案

1.1 工程背景及总体优化思路

增压器压气机变海拔优化设计的应用对象是某车用增压中冷发动机，主要参数见表1。

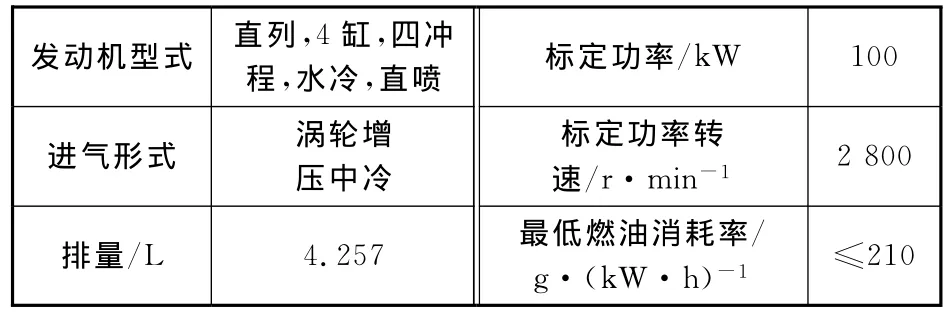
表1 发动机参数

根据试验数据，该发动机在海拔2 500m时功率下降明显。为了使发动机能达到较好的变海拔性能，现需要对增压器进行优化设计，使增压器在海拔0～2 500m都具有较好的工作性能。表2所列为海拔0m和海拔2 500m下的大气条件参数［8］。

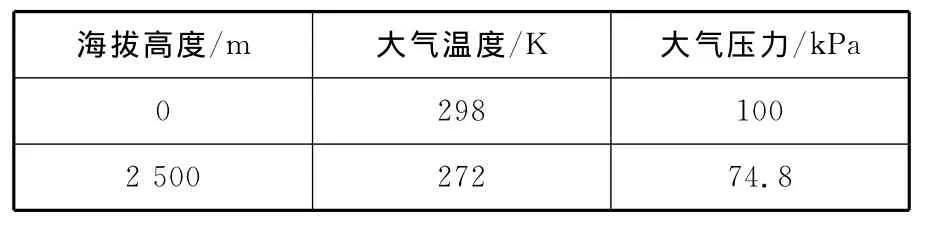
表2 海拔0m和海拔2 500 m时大气条件参数表

由发动机在海拔0m下设计点（即发动机标定点）对应的压气机等效流量和压比可折算出海拔2 500m大气条件下对应的理论折合流量和压比（见表3）。

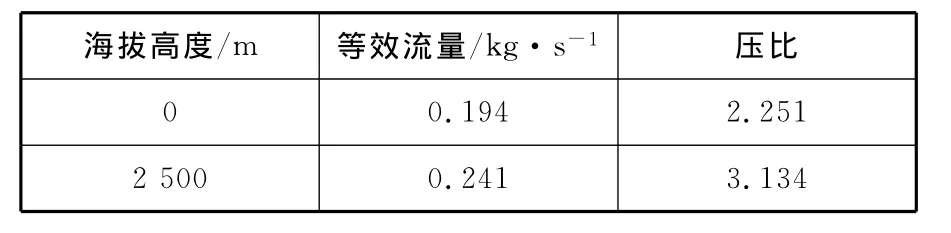
表3 不同海拔下压气机设计点理论参数

本研究提出的压气机变海拔优化设计思路见图1。首先，针对变海拔工作条件，初步确定压气机的虚拟工况点，设计得到压气机的原型虚拟数字样机（图1中上部小虚线框所示）；然后在原型压气机的基础上针对变海拔工作的需求，设定多目标优化目标函数和优化变量，通过一定的优化方法最终得到变海拔性能最优的压气机结构参数（图1中下部大虚线框所示）。

原型压气机的设计是假设大气条件为海拔0m和海拔2 500m的平均值（海拔1 250m），即大气环境温度为285K，大气压力为87.4kPa；同时，假设发动机在该海拔条件下标定工况时功率、燃油消耗率等性能参数基本不变，计算得到的压气机设计点折合流量为，压比为πc＝2.52；然后通过Concepts NREC叶轮机械设计软件得到满足这个性能参数的初始压气机几何结构。

1.2 多目标优化函数建立［6］

提出的优化目标可使压气机的变海拔工作性能达到最佳。具体来说，首先要确保在海拔0m和海拔2 500m大气条件下，压气机在发动机标定功率点的等熵效率最大。分别记海拔0m和海拔2 500m条件下压气机的等熵效率为ηst和ηal，则在ηst＜1和ηal＜1的前提下，希望ηst和ηal最大限度地接近1，所以ηst和ηal存在最大允许阈值ηrefst＝1和ηrefal＝1，即该约束为不等式约束。同时，还希望海拔0m和海拔2 500m条件下压气机的压比尽量接近对应海拔下发动机标定工况时的压比。分别记海拔0m条件和海拔2 500m条件下压气机的压比为πst和πal，根据表3中数据，发动机标定工况时在海拔0m和海拔2 500m条件下分别对应的理论压比为πrefst＝2.251和πrefal＝3.134，所以，πst和πal应尽量接近πrefst和πrefal，即该约束存在等值约束。

根据以上分析，拟将压气机变海拔多目标优化问题的目标函数写为惩罚函数的型式，其表达式可以初步确定为

式中：wstη，walη，wstpr，walpr分别为各惩罚项的惩罚权重因子；xstη，xalη，xstpr，xalpr分别为各惩罚项的指数。

设计时假设在海拔0m和海拔2 500m条件下，各惩罚项的变化对目标函数值的影响程度相同或同等重要，则应赋予效率项和压比项各自拥有相同的权重值和指数，即假设 wstη＝walη＝wη，wstpr＝walpr＝wpr且xstη＝xalη，xstpr＝xalpr。xstη，xalη按照惩罚函数的常规定义取值，取xstη＝xalη＝2。对于压比项，由于在相同情况下比效率项更可能等于0，对目标函数值的影响比效率项更显著，所以，为凸显压比惩罚项的效果，取xstpr＝xalpr＝4。

为了估算各权重值，假设目标函数中一个压比项的压比值变化为5%时，对目标函数值造成的影响与一个效率项效率变化5%时的效果相同，同时，假设效率由75%提高到80%，则有：

由式（2）计算得：

令wη＝1，则wpr＝3 600。

通过以上的假设和估算，目标函数最终确定为

1.3 几何约束与初始参数数据库的建立

多目标优化过程是通过改变原型压气机叶型的几何参数值来实现的。因此，首先需要将初始叶型进行离散并利用已知的曲线段进行参数化拟合，该过程可通过Numeca软件中的AutoBlade模块实现。为了在保证优化效果的前提下，尽量减少CFD计算工作量，本研究只选择对压气机效率影响最大的主叶片的叶根和叶顶的中弧线进行参数化拟合。选用Bezier曲线进行拟合控制，在中弧线上分布了10个控制点，即10个设计变量，所以，每个主叶片的叶根和叶顶的中弧线加起来共有20个设计优化变量。表4列出20个设计优化变量默认取值的变化范围，原型压气机对应的变量值为中间列。

确定了压气机主叶片几何优化参数的数量和取值范围之后，需要获得一定数量的样本参数进行优化之用。根据Numeca公司推荐资料，生成样本数应为自由变量数的2～3倍［9］。利用Numeca软件中的Design3D模块进行自动选择，得到了49组有关压气机叶片参数的初始样本点，并形成样本库。

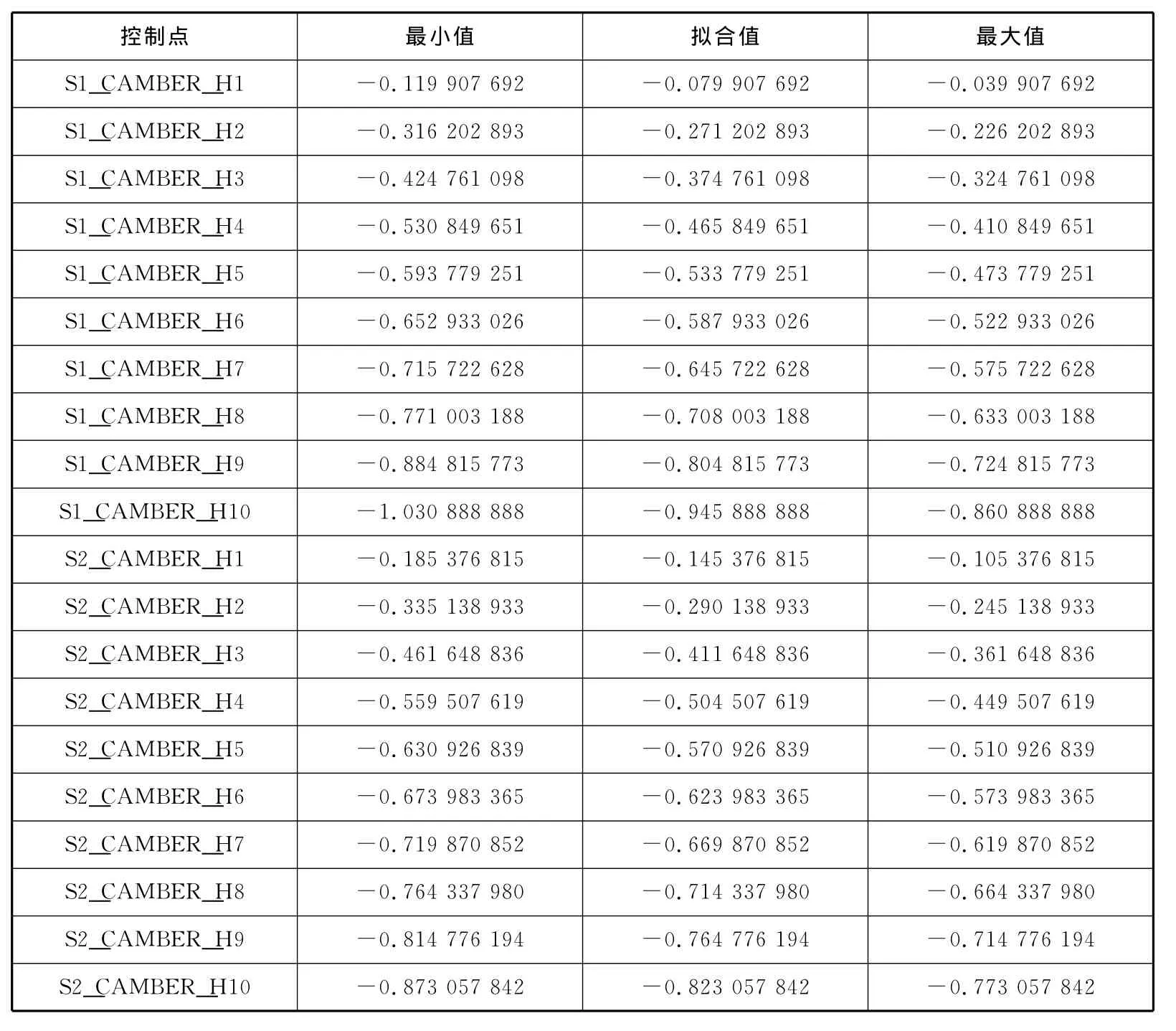
表4 压气机主叶片叶根和叶顶中弧线拟合参数及其变化范围

1.4 多目标优化方法

采用Numeca/Design3D软件进行压气机的多目标优化［9］。该软件采用的优化技术是基于函数近似的概念，将人工神经网络和遗传算法联合起来使用。具体步骤如下：

1）对选择的49种压气机叶片形状进行CFD计算，获得每种叶型的压气机性能参数，形成压气机性能的样本数据库；

2）采用人工神经网络方法对数据库中的样本数据进行拟和，获得叶片几何参数与目标函数的关系，接着利用遗传算法预测在拟合出的函数关系下使目标函数值减小的新数据点，即新的几何叶型；

3）对预测得到的最优叶型利用Numeca软件进行CFD计算，获得新叶型的性能参数；

4）如果CFD计算结果使目标函数值减少，则将该数据点扩充初始数据库，然后重复2），……，如此循环，直到达到较好的计算结果。优化过程见图2。

2 压气机多目标优化结果及分析

优化过程目标函数值随迭代次数增加而变化的情况见图3。由图3可以看出，优化开始时，软件利用人工神经网络（ANN）和遗传算法预测得到的目标函数值远远小于CFD计算结果，但随着优化次数的增加，预测结果逐渐增大，CFD计算结果逐渐下降，二者逐渐趋于一致。在优化次数达到第30次时，预测值基本接近CFD计算值，优化基本达到要求。

根据目标函数值的大小，选出优化结果中较好的第13代、第24代和第29代，其相应性能参数见表5。

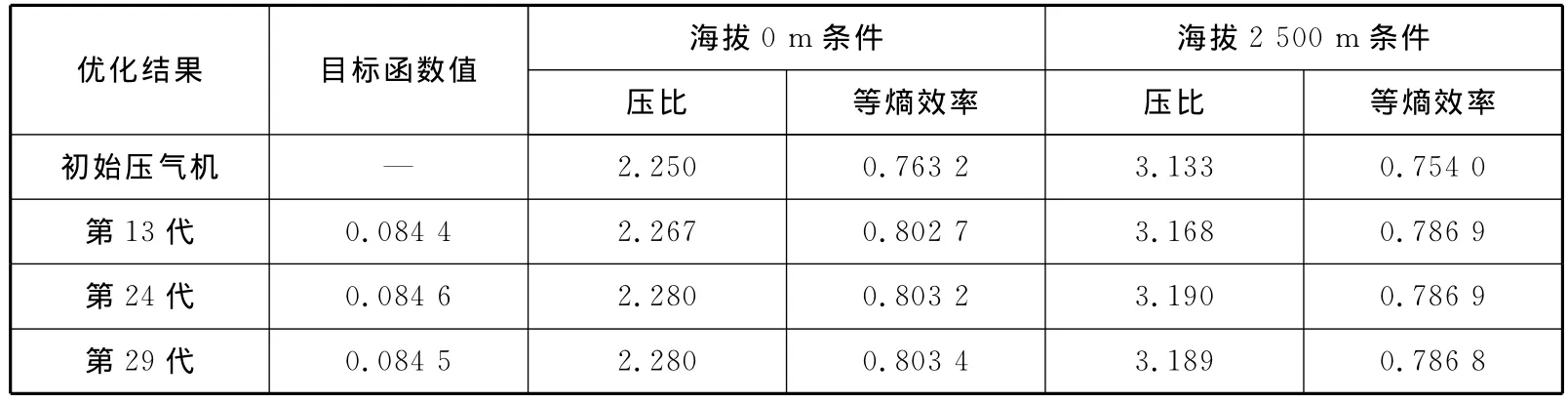
表5 多目标优化结果比较

由表5可知，以上3组数据目标函数值的差别较小。对于目标函数最小的第13代结果，其压比值最接近初始压气机，同时，其等熵效率值在海拔0m和海拔2 500m工作条件下比初始设计值分别提高了3.95%和3.29%。

3 结束语

通过构造以惩罚函数为型式的目标函数，应用多目标优化设计方法进行压气机的变海拔性能优化设计，对改善车用增压发动机增压器的变海拔工作性能具有工程参考价值。

［1］ 王 军.WD615系列高原柴油机的开发［D］.天津：天津大学，2003.

［2］ 程晓青.高原低温环境对工程机械的影响及对策措施［J］.青海科技，2002（4）：30－34.

［3］ 张海雷.柴油机变海拔涡轮增压技术研究［D］.北京：清华大学，2008.

［4］ 宋立明，李 军，丰镇平，等.基于多目标优化的透平叶栅变工况设计方法［J］.海空动力学报，2007（9）：1499－1504.

［5］ 樊会元，席 光，王尚锦.基于遗传算法的离心压缩机叶栅多点优化设计［J］.工程热物理学报，2000（3）：174－177.

［6］ Demeulenaere A，Ligout A，Hirsch C.Application of Multipoint Optimization to the Design of Turbomachinery Blades［C］.ASME Paper GT2004－53110，2004.

［7］ 赵洪雷，王松涛，韩万金，等.多级涡轮多工况气动优化设计研究［J］.航空动力学报，2008（1）：106－111.

［8］ 柯亚仕，高桐生.非增压车用柴油机高原性能预测方法［J］.西安交通大学学报，1990（3）：123－128.

［9］ He K，Chen Z P，Yuan X.Aerodynamics Optimum Design of Blades in Centrifugal Compressor［J］.Journal of Engineering Thermophysics，2009，30（3）：393－396.