一种新型电磁线圈发射器的动态特性

陈学慧 曹延杰 王成学 王慧锦

（海军航空工程学院 烟台 264001）

1 引言

同步感应线圈发射器是电磁线圈发射器的一个重要分支，它的电枢电流由驱动线圈中的单脉冲电流感应产生，有驱动线圈和电枢无机械接触、效率高等诸多优点[1-6]。同步感应线圈发射器是利用洛伦兹力来加速筒状电枢的，电枢中的感应电流和所受电磁力主要集中在后端部。当感应线圈中的电流很大时，电枢中的电流和电磁力会很大。由于电流和应力过于集中，从而容易导致电枢后端部发生变形甚至烧蚀[7-9]。而化学能发射器直接推动弹丸运动的是弹底压力，弹底压力越高，弹丸获得的加速度越大[10]。受化学能推进的启发，在同步感应线圈发射器的筒状电枢后部增加一个圆盘电枢，再在圆盘电枢下增加一个圆盘线圈便可在电枢的底部获得相当大的弹底电磁力。鉴于这种设计思想，本文提出了一种新型电磁线圈发射器，它在第一级利用螺旋线圈和圆盘线圈共同推动电枢沿轴向运动[11,12]，改善了电枢的受力分布。

本文对新型线圈发射器进行了电路与运动特性仿真分析，得到了驱动线圈的电流、电枢所受电磁力和速度；对三维有限元模型进行了电磁场仿真，得到了电枢三维涡流分布和驱动线圈磁场密度分布，并用磁-结构耦合方法得到了驱动线圈的应力分布，为新型电磁线圈发射器的进一步研究奠定了基础。

2 结构组成和工作原理

新型电磁线圈发射器模型如图1所示，主要由储能电容、同步触发控制电路及开关、驱动线圈和新型电枢等组成，发射时第一级的圆盘线圈和螺旋线圈同时馈电，然后其余各级螺旋线圈依次馈电。工作原理如下：首先同时闭合第一级圆盘线圈和螺旋线圈的驱动电路开关，根据电磁感应定律，当圆盘线圈和螺旋线圈各自通以变化的电流时，在两个线圈的周围产生的磁场亦是变化的，可知电枢中有感应电流产生，电流产生的磁场相互作用，在圆盘线圈、螺旋线圈和电枢之间产生洛伦兹力。轴线方向的洛伦兹力推动电枢垂直向上运动，当电枢到达第二级螺旋线圈适当位置时闭合第二级电路开关，给第二级螺旋线圈通电，电枢又被感应出和该螺旋线圈中电流方向相反的电流，再次受到向上的排斥力继续被加速。同理，进入后面的螺旋线圈，电枢被不断地加速驱动，直至最后飞离发射器。

图1 新型电磁线圈发射器模型Fig.1 Model of the new electromagnetic launcher

相对同轴电磁线圈发射器来说，新型发射器在第一级增加了螺旋线圈和平板电枢。本文只对新型发射器的第一级进行分析，以后各级的分析与同轴电磁发射器基本相同。

3 数学模型

3.1 电路方程

发射器第一级电路模型如图2所示。

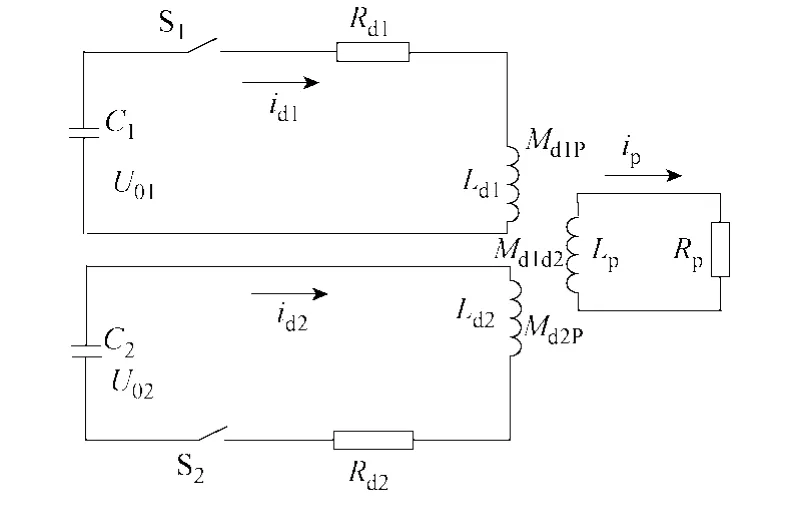
图2 新型发射器第一级线圈驱动电路Fig.2 Drive circuit of the first stage

图2中C1、C2分别是圆盘线圈和螺旋线圈驱动电路电容器组。Rd1、Rd2是放电回路电阻，包括驱动线圈电阻、电容器电阻、放电开关电阻和接线电阻等。Ld1、Ld2是电路电感，包括驱动线圈电感、电容器电感、放电开关电感和接线电感等。id1、id2是驱动线圈中的电流。Rp、Lp、ip分别是电枢电阻、电感和电枢中的电流。在某一t时刻电路方程如下

3.2 电磁力方程

采用电感法计算弹丸所受推力，t时刻新型电磁线圈炮中的总储能

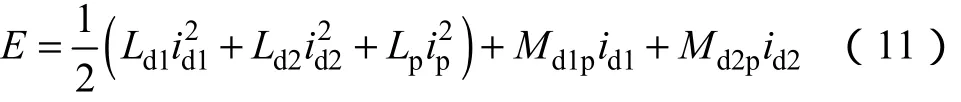
电枢运动方向为x方向，自感磁能不变化，Ld1与Ld2因为固定，它们的互感也不变化，只有互感项Md1p、Md2p磁能随x变化。t时刻作用在电枢上沿x方向的力为

由式（12）可以看出，要得到电枢x方向的推力，还需要计算驱动线圈与电枢沿x方向上的互感梯度。在新型电磁线圈发射器中，螺旋线圈、圆盘线圈和电枢的互感和互感梯度可以通过查表或者Kirchhoff方法计算得到[13,14]。

电枢的速度如下所示

式中ma——电枢的质量。

3.3 电磁场控制方程

新型电磁发射器的整个区域V可以分成涡流区域V1和非涡流区域V2。涡流区域指电枢，非涡流区域指螺旋线圈、圆盘线圈和其它非导电介质，包括绝缘体和周围部分空气。若忽略位移电流，根据麦克斯韦方程组和涡流场的准静态条件，在发射过程中磁场和涡流场的控制方程用A和φ -A方法描述如下[15]。

式中A——磁向量势；

v——磁阻率；

φ——电标势；

σ——电导率。

3.4 应力场控制方程

在发射过程中，驱动线圈和电枢之间的力是时变的，在时变的驱动线圈磁场分布和瞬态的电枢的感应电流之间存在非常复杂的关系。因此可以在相对较短的时间里把它当成静态来分析，即假设电枢在某一个时间段内固定在某个位置，驱动线圈分别由相应时间的电流段来馈电[16]。基于弹性理论，张量形式的应力场的控制方程表示如下[17]

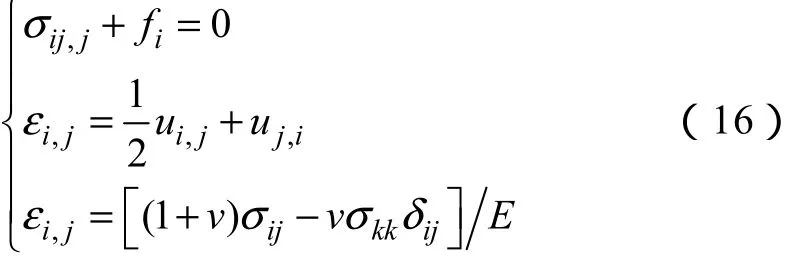
式中σij,j——应力；

fi——体积力；

εi,j——应变；

u——位移；

E——杨氏模量；

v——泊松比；

i，j，k=1，2，3。

4 场路耦合分析

4.1 物理模型

图3为新型发射器第一级的结构参数示意图。驱动线圈的材料为铜，电枢的材料为铝。圆盘线圈和螺旋线圈的匝数分别为15匝和40匝，电枢总重0.27kg，各参数取值见表1。

图3 新型发射器第一级结构剖分图Fig.3 The structural diagram of the first stage

表1 新型发射器第一级各参数取值Tab.1 Parameters of the first stage（单位：mm）

4.2 电路和运动特性仿真

假设螺旋线圈和圆盘线圈的驱动电路参数相同，如图4所示。为了阻止对电容器的反向充电，在驱动线圈的两端并联了硅堆D[18]。电容器C的初始电压是 4kV，容量为 1 000μF，R1、R2和R3分别是 0.01Ω、0.03Ω 和 0.01Ω。

图4 带硅堆的驱动电路图Fig.4 Circuit of the drive coil with diode

使用前向差分法计算电枢电流

式中ma——电枢的质量；

va——电枢的速度；

x——电枢的位移。

仿真结果如图5和图6所示。从图5可以看出圆盘线圈的电流峰值更大（约 48kA），到达峰值的时间更短（约 0.05ms）；螺旋线圈中的电流比圆盘线圈平缓，但是在较长的时间内能够保持相对较大的幅度（＞7kA）。从图 6可以看出在 0.05ms有一个时间较短的力脉冲，峰值是360kN，接着有一个幅值超过50kN，时间超过0.2ms的持续力。电枢在0.15ms前速度增加很快，而之后速度增加变慢，这是由于电枢在0.15ms前主要由圆盘线圈加速，而之后主要由螺旋线圈加速。

图5 新型发射器中驱动线圈电流波形Fig.5 Current curves of the drive-coils

图6 电枢受力和速度波形Fig.6 Force and speed’s curve in armature

4.3 电磁场仿真分析

驱动线圈三维有限元模型如图7所示，螺旋线圈被分为15 999个单元和36 008个节点，圆盘线圈被分为13 270个单元和23 904个节点。螺旋线圈由高45mm，内径62mm，外径102mm的绝缘材料浇铸；圆盘线圈由高12mm，内径4mm，外径64mm的绝缘材料浇铸；材料特性见表2。

图7 螺旋线圈和圆盘线圈的三维有限元模型Fig.7 3D finite element model of HC and PC

表2 材料属性Tab.2 Material properties

模型中驱动线圈的馈电电流采用如图5所示的数据，电枢在不同时刻的位置可根据电路和运动特性仿真分析得到了电枢速度计算得到。仿真中使用第一类磁场边界条件，即磁向量势A设置为零。电枢在0.05ms时的电流密度矢量如图8所示，驱动线圈的磁通密度矢量如图9所示。

图8 0.05ms时电枢的电流密度矢量图Fig.8 Current density vectors in armature at 0.05ms

图9 0.05ms时驱动线圈的磁通密度矢量图Fig.9 Magnetic density vectors in drive coils at 0.05ms

5 磁结构耦合分析

为了分析发射装置的强度，对三维有限元模型进行了磁结构耦合仿真。仿真中位移边界条件是绝缘体的外边界位移为零。

电枢在0.05ms时的节点电磁力向量如图10所示，各个分量的值如表3所示。Force-X代表轴向力，其值比电路仿真数值大 25.6%，主要是因为在磁结构耦合中电枢在这个时间段没有运动，电枢和圆盘线圈的距离在大部分时间里都小于实际中的距离；Force-Y和Force-Z分别代表在Y和Z方向的径向力，其数值远小于轴向力的数值。由表3可知，三维模型的径向力并不是均匀分布的，Y和Z方向的径向力有可能导致电枢与管壁的接触从而降低发射器的性能。

图10 0.05ms时电枢节点电磁力矢量图Fig.10 Nodal electromagnetic force vectors in armature at 0.05ms

表3 电枢在0.05ms时的受力表Tab.3 The total force in armature at 0.05ms

图11 0.25ms时圆盘线圈Von Mises应力图Fig.11 Von Mises stress of PC at 0.25ms

图12 0.25ms时螺旋线圈Von Mises应力图Fig.12 Von Mises stress of HC at 0.25ms

图13 0.05ms时圆盘线圈Von Mises应力图Fig.13 Von Mises stress of PC at 0.05ms

图14 0.05ms螺旋线圈时Von Mises应力图Fig.14 Von Mises stress of HC at 0.05ms

驱动线圈的应力分布如图11～图14所示。从图中可以看出在圆盘线圈的电流达到峰值时（0.05ms），圆盘线圈的最大Von Mises应力为234MPa，螺旋线圈的最大Von Mises应力为1.26MPa；在螺旋线圈的电流达到峰值时（0.25ms），圆盘线圈的最大Von Mises应力为 51MPa，螺旋线圈的最大 Von Mises应力为17.3MPa，均小于铜的屈服应力280MPa。

6 结论

新型电磁发射器能够在第一级产生较大推力，非常适合于大质量载荷的发射。仿真结果显示电枢在发射期间同时被两个驱动线圈加速，在驱动电流到达峰值时，线圈能够承受相应的机械应力，具有较好的强度性能。

[1] Kaye R J. Operational requirements and issues for coilgun EM launchers[J]. IEEE Transactions on Magnetics, 2005, 41(1): 194-199.

[2] Lockner T R, Kaye R J, Turman B N. Coilgun technology, status, applications, and future directions at Sandia National Laboratories[J]. IEEE Transactions on Magnetics, 2004, 40(1): 119-121.

[3] Barry M. SLINGSHOT——a coilgun design code[R].SAND2001-1780, Albuquerque, New Mexico: Sandia National Laboratories, 2001.

[4] Kaye R, Turman B, Aubuchon M, et al. Induction coilgun for EM mortar[J]. IEEE Transactions on Magnetics, 2007, 43(1): 1810-1813.

[5] Kaye R J, Tuman B N, Shope S L. Applications of coilgun electromagnetic propulsion technology[J].IEEE Transactions on Magnetics, 2002, 38(1):703-707.

[6] Andrews J A. Coilgun structures[J]. IEEE Transactions on Magnetics, 1993, 29(1): 637-642.

[7] 曹延杰，刘文彪，邹本贵，等. 三级同步感应线圈炮内弹道过程仿真[J]. 弹道学报，2008，20(4): 92-95.Cao Yanjie, Liu Wenbiao, Zou Bengui, et al. Interior ballistics motion simulation of three-stage synchronous inductive coilgun[J]. Journal of Ballistics, 2008, 20(4):92-95.

[8] 邹本贵，曹延杰，王成学，等. 单级同步感应线圈炮电枢的磁场-温度场有限元分析[J]. 电机与控制学报，2011，15(2): 42-47.Zou Bengui, Cao Yanjie, Wang Chengxue, et al.Analysis of magnetic-thermal fields for armature in single-stage synchronous induction coilgun[J].Electric Machines and Control, 2011, 15(2): 42-47.

[9] Andrews J A, Devine J R. Armature design for coaxial induction launchers[J]. IEEE Transactions on Magnetics, 1991, 27(1): 639-643.

[10] 金志明. 高速推进内弹道学[M]. 北京: 国防工业出版社，2001.

[11] Liu W B, Cao Y J, Zhang Y, et al. Parameters optimization of synchronous induction coilgun based on ant colony algorithm[J]. IEEE Transactions on Plasma Science, 2011, 39(1): 100-104.

[12] Wang C X, Cao Y J, Zou B G, et al. Research on EM launcher of active EM armor with field-circuit coupled method[J]. IEEE Transactions on Plasma Science, 2011, 39(1): 481-486.

[13] 雷银照. 轴对称线圈磁场计算[M]. 北京: 中国计量出版社, 1991: 209-215.

[14] 李军峰, 李文杰. 航空电磁发射线圈自感系数的精确计算[J]. 物探化探计算技术，2007，29(增刊): 17-20.Li Junfeng, Li Wenjie. A calculation method of self-inductance of transmiting coil for AEM system[J].Computing Techniques For Geophysical And Geochemical Exploration, 2007, 29(supl): 17-20.

[15] 谢德馨, 杨仕友. 工程电磁场数值分析与综合[M].北京: 机械工业出版社，2008.

[16] Wang D M, Liu P, Liu H Q, et al. The design and structure analysis of a coilgun for low acceleration of heavy loads[J]. IEEE Transactions on Magnetics,1999, 35(1): 160-165.

[17] Zou B G, Cao Y J, Wu J, et al. Magnetic-structural coupling analysis of armature in induction coilgun[J].IEEE Transactions on Plasma Science, 2011, 39(1):65-70.

[18] Zhao K Y, Cheng S K, Zhang R P. Influence of driving current’s wave on accelerative performance of induction coil launcher[J]. IEEE Transactions on Magnetics, 2008, 44(1): 1-4.