相干两点源对比相单脉冲测角的干扰机理分析*
杨立明,吕 涛,陈 宁
(1空军装备研究院雷达与电子对抗研究所,北京 100085;2电子信息控制国家重点实验室,成都 610036)
0 引言
单脉冲测角体制因为其良好的抗干扰能力而被广泛应用,普通的噪声干扰对其作用不明显[1]。在主动雷达导引头上也被广泛采用。主动雷达制导导弹可以实现“发射后不管”,射程远、精度高,是未来空战的主要武器,对战斗机的安全造成了很大威胁。因此,为了提高载机平台在面对主动雷达制导导弹威胁时的生存力,必须解决对单脉冲导引头的角度诱骗,以有效保护载机。
目前,对单脉冲测角体制的干扰手段有非相干和相干干扰[5],前者的实现方法有拖曳诱饵或者伴飞诱饵,这已经在诸多装备上得到实现。而后者由于其工程实现的难度较大而一直没有工程实现,有关报道不多。文中通过对相干两点源对单脉冲体制的干扰机理进行深入分析,并对实际应用中对干扰效果可能存在的影响因素进行了分析,分析结果对相干两点源的发展具有重要的参考价值。
相干两点源是指具有稳定可控的相位关系的两个辐射源[4]。通过合理的控制,可以在单脉冲雷达天线口面产生相位波前畸变,使得单脉冲雷达跟踪角偏离正确的方向[2-7]。相干两点源对单脉冲雷达角跟踪的干扰机理集中在对比幅单脉冲的分析,对比相单脉冲的干扰机理的系统分析则未见报道。文献[8]从单脉冲天线理论的角度分析了对比相单脉冲的干扰效果,没有从比相测角的角度分析单脉冲的干扰机理。虽然比幅单脉冲和比相单脉冲是等价的[9],但是文中认为有必要系统分析相干两点源对比幅单脉冲的干扰机理,完善该干扰理论。相干两点源干扰是对单脉冲雷达干扰的重要手段。相干两点源可以用双机配合实现,也可以在单机上通过两个具有一定基线距离的相干点源实现。二者的干扰机理类似,但是实现方法不同。文中的分析以单机实现的相干两点源为例。
1 相位单脉冲测角原理
相位单脉冲测角原理如图1所示。远场信号到达雷达接收天线时可以近似看作平面波,相位法测向时,两天线相隔一定距离l,目标回波信号(以M点发出)到达两天线的路径差不同,天线1接收信号的相位比天线2的相位滞后一个Δφ值,信号的到达方向角为θ,即有:
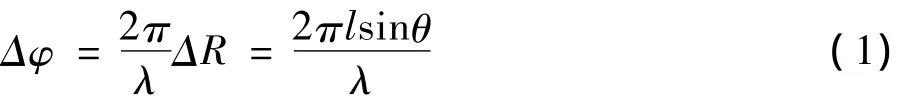
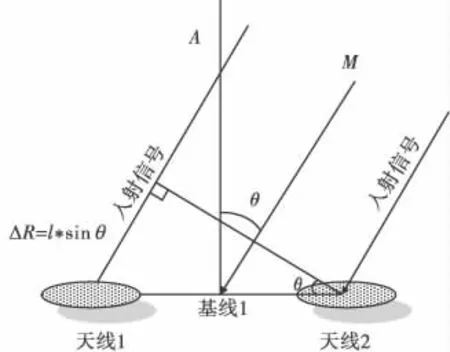
图1 相位法单脉冲测角原理
在λ和l确定后,Δφ与θ成正比,式中θ是目标方向的偏角,λ为雷达的工作波长。因此,根据式(1)可以推导出回波信号到达角计算公式:

2 相干两点源对单脉冲测角性能干扰机理分析
2.1 对比幅单脉冲的干扰机理[3]
在讨论问题之前,需要规定一些约束条件,以简化分析过程,但得到的结论不失一般性。单脉冲角跟踪一般在很小的角度范围(半波束宽度内)进行,超出该范围有其它测角系统进行引导。由于角度欺骗干扰也是在小角度范围进行,一般不会超出半波束宽度,都是在小角度条件下展开分析的。对比相单脉冲的干扰机理分析也是基于此前提下进行的。
设相干两点源J1、J2如图3所示。它们频率相同,辐射信号可以表示为:

其中:AJ1、AJ2分别为两信号的幅值;φ1、φ2分别为两信号的初始相位;θ0表示导引头天线方向图峰值方向与瞄准轴之间的交角;Δθ表示导引头天线相对两点源的张角(绝对值);θ1表示右边干扰源1与瞄准轴的夹角;θ2表示左边干扰源2与瞄准轴的夹角;θc是相干两点源中心线与瞄准轴之间的交角。为了更直观的分析,文中将图2用笛卡尔坐标系表示,如图3所示。
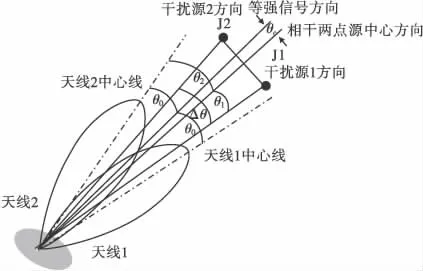
图2 相干两点源干扰下导引头测角示意图
图3 笛卡儿座标下导引头测角示意图
相干两点源对比幅单脉冲干扰的角度诱偏公式为[6]:

式(5)就是主动末端对抗技术产生角度诱偏的一般表达式。式中:θc是误差角;Δθ是两点源相对雷达的张角;β是两个信号振幅比;φ是两个信号相位差。
当φ=π时,式(5)变为:

由式(6)可知,β=1或接近 1时,θc≥Δθ,雷达偏出两点源之外的角度。利用式(5),选用不同的φ和β值,计算的曲线如图4所示。
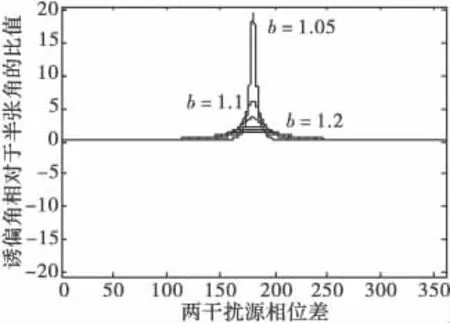
图4 主动末端对抗技术干扰效果和幅度比/相位差的关系
由图4可以得出:
1)β越接近1,φ=π时,干扰造成的误差就大。但在φ的其它值时,干扰效果降低得很快。
2)增加β值时,虽然φ=π时的干扰效果迅速降低,但这时的曲线随φ的增加或减少变化缓慢,干扰的稳定性较好。
3)雷达跟踪的方向靠近功率稍大的辐射源。
2.2 对比相单脉冲的干扰机理
图5为相干两点源干扰情况下比相单脉冲系统测角示意图。
图5中L1、L2分别为雷达两比相天线的相位中心,L1、L2连线的法线方向为雷达瞄准方向(DL射线)。为了讨论干扰角的偏转方向,同时假设雷达瞄准轴方向为零,右边角度为正。定义θ为雷达瞄准误差角,即两点源中心点与雷达中心连线OD相对于瞄准轴的夹角,设:


图5 两点相干源干扰下比相单脉冲系统测角示意图
则(O1、O2)在L1形成的合成场为:
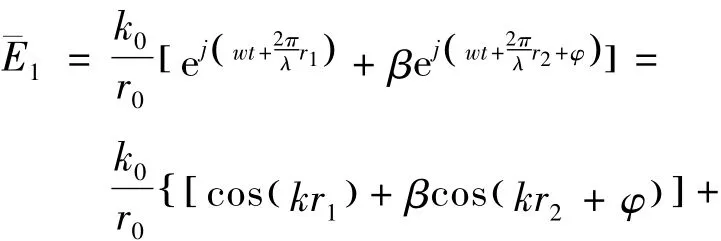
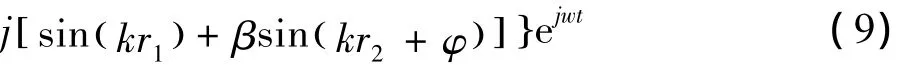
其中:


同样可以得到L2的相位为:

比相系统跟踪稳定的条件是 L1、L2的相位差为零:

将式(11)、式(12)分别代入方程(13)得到:
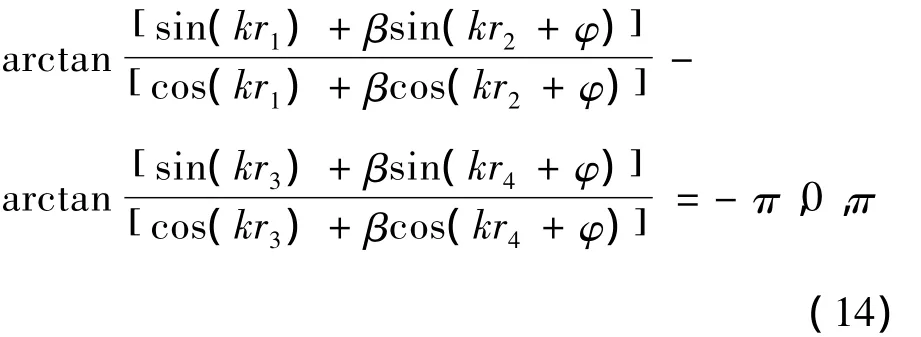
将式两边同时取正切:

利用三角函数的加法定理将其展开:

则可知式(16)中的分子为零,展开可得下式:
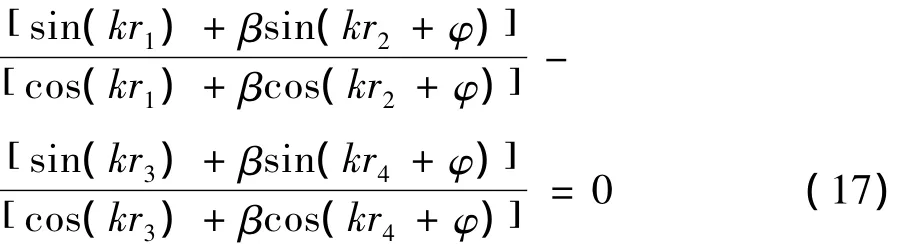
利用三角函数和差化积的公式,可对式(17)化简得到下式:
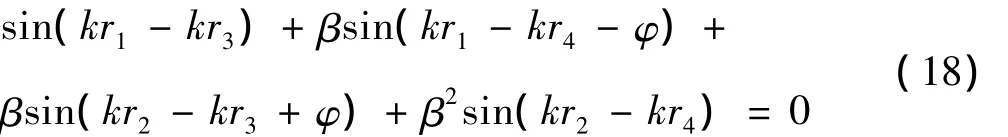
对式(18)进一步整理可得到下式:
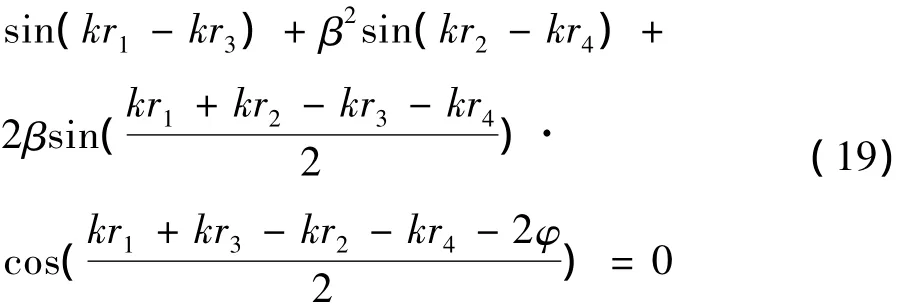
当 r0≫L,时,可做如下近似:θ1=kr1- kr3、θ2=kr2-kr4,其实际意义分别表示O1和O2与雷达瞄准轴的夹角。
设Δθ为两点源相对于雷达口面的张角。θ1=θ-另外,设δ1=k(r1- r2);δ2=k(r3-r4);
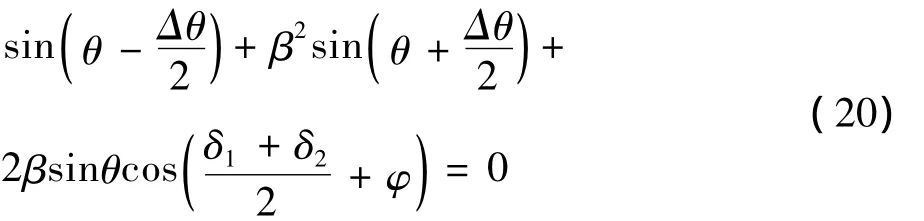
将式(20)展开后得到下式:
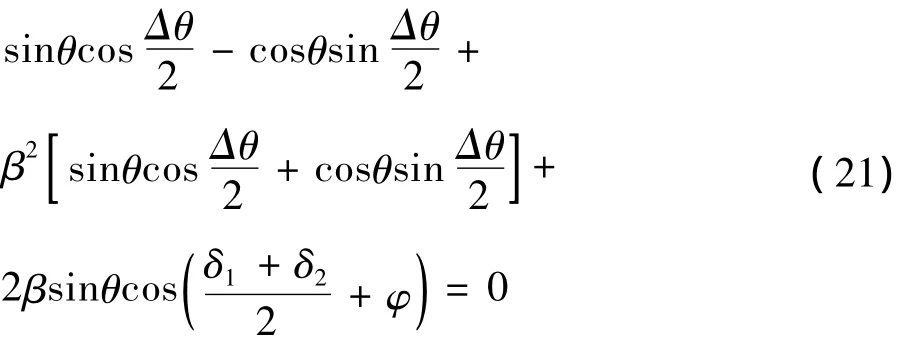
当θ、Δθ都为小角度时,可近似认为:

对式(24)作进一步整理可得下式:
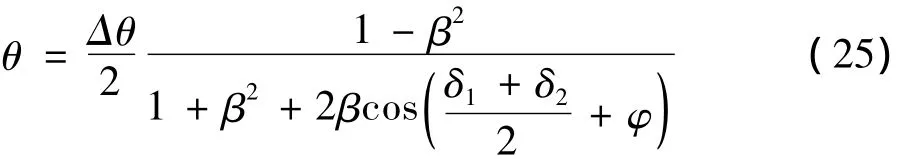
由式(25)可知,相干两点源对比相单脉冲的干扰角除了与两点源的幅度、相位有关外,还与它们与雷达的几何位置有关,由于几何位置引入的相位极其不确定,在工程上,通常采用双通道的干扰结构或者相位测量-补偿的方式消除传播路径的不确定性。如果通过某种手段使,式(25)变为:
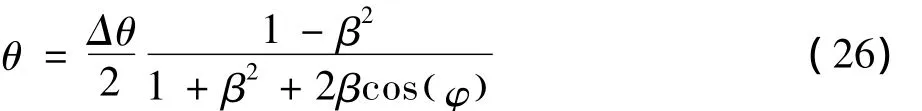
这里得到了与比幅单脉冲系统完全相同的角度干扰的公式,通过该式,可进一步分析干扰角的偏转方向:当E1>E2、β<1,θ>0,即出现图中的情况,瞄准轴靠近O1;当E2>E1、β>1,θ<0,瞄准轴靠近O2,即雷达瞄准轴始终偏向功率较大的干扰源。
总之,在小角度情况下,两点相干源对比相单脉冲的干扰效果与对比幅单脉冲的干扰效果完全一致,这说明两点相干源干扰,无论对比幅单脉冲还是比相法单脉冲都能产生相同的干扰效果。其实,无论是比幅单脉冲还是比相法单脉冲系统,都是跟踪信号的相位波前方向,相干两点源在雷达口面产生的相位波前与所采用的测角方法无关,因此产生完全一致的结论是理所当然,通过文中的推论,再次证明两点相干源对比相单脉冲的角度干扰也是有效的。
3 结论
针对单脉冲测角原理,在已有的基础上,详细分析了相干两点源对比相单脉冲雷达的干扰机理,并得出与比幅单脉冲雷达一致的角度诱骗量计算公式,文中的研究对于相干两点源干扰系统的研制和使用具有较强的参考价值。
[1]Arnold D Seifer.Monopulse-radar angle tracking in noise or noise jamming[J].IEEE Transaction on Aerospace and E-lectronic Systems,1992,28(3):622-638.
[2]N M Harwood,W N Dawber,V A Kluckers,et al.Multiple-element cross-eye[J].IET Radar Sonar Navig.,2007,1(1):67-73.
[3]C Musso,C Curt.Robustnes s of a new angular countermeasure[C]//Proc.Radar 97,1997:415-419.
[4]陈宁,蒋勇.相干两点源对单脉冲角跟踪诱偏方向的研究[J].电子对抗,2009(3):6-9.
[5]林象平.雷达对抗原理[M].西安:西北电讯工程学院出版社,1985:317-355.
[6]L B Van Brunt.Applied ECM[M].New York:EW Engineering,Inc.,1978,Vol.1.
[7]J H Dunn,D D Howard.Radar target amplitude,angle,and Doppler scintillation from analysis of the echo signal propagating in space[J].IEEE Trans.Microw.Theory Tech.,1968,9(9):715-728.
[8]W Pdu Plessis,J W Odendaal,J Joubert.Extended analysis of retrodirective cross-eye jamming[J].IEEE Transactions on Antenna and Propagation,2009,57(9):2803-2806.
[9]S M Sherman.Monopulse principles and techniques[M].Boston:Aretech House,1984.

