改进的小波阈值算法在红外图像去噪中的应用*
沙俊名,刘泽乾,庞 帅,夏志申
(空军航空大学航空军械工程系,长春 130022)
0 引言
航空武器在制导末段获取红外图像过程中,由于受恶劣外界环境条件和探测器本身固有特性的影响,不可避免的产生大量噪声。这些噪声主要包括热噪声、散粒噪声、电流噪声、复合噪声等,并可以用高斯模型来描述[1]。这些噪声对红外图像后期的分析和处理带来很大影响,因此,图像去噪成为航空武器红外图像处理中不可或缺的重要部分。传统的去噪方法如:直方图滤波、维纳滤波和中值滤波等,虽然算法简单,硬件实现方便,但在复杂背景条件下去噪效果显得力不从心。近年来,基于小波变换的去噪方法成为目前图像去噪的主要手段之一。小波变换以其基于频率域内信号与噪声谱不重叠的思想保证了图像细节信息不丢失,同时小波还具有低熵性、多分辨率、去相关性、选基灵活性等优点,使得小波变换在图像去噪中具有独特的优势。
文中在Donoho提出的小波阈值去噪算法基础上对阈值函数和阈值选取方法分别加以改进,提出了一种改进的小波去噪算法,并将其应用于航空武器获取到的红外图像上。通过建立评价体系,将该算法与传统阈值算法、维纳滤波算法以及中值滤波算法的处理结果进行进一步定量分析,以证明该方法在红外图像去噪中的优势。
1 小波变换原理
1.1 小波变换
与傅里叶变换不同,小波变换的基础函数是一些具有变化的频率和有限持续时间的小型波,称为小波,它被认为是数学显微镜。小波变换定义为:把一个称为基本小波的函数ψ(t)做位移τ后,在不同尺度a下与待分析信号x(t)做内积:
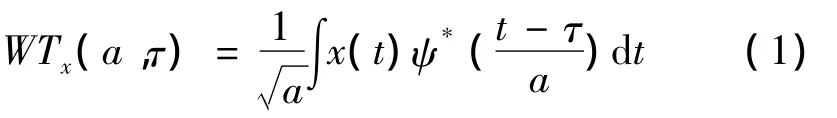
其中ψ*为ψ的共轭。从式(1)可以看出小波变换的实质是用一个合适的基小波ψ(t)通过时间轴上的位移与缩放和幅度的变化产生一系列派生小波,用系列小波对要分析的信号进行时间轴上的平移比较,获得用以表征信号与小波相似程度的小波系数,从而获得傅里叶分析不能获得的局部时间区间信息。小波函数ψ(t)存在许多可选性,如非正交小波、正交小波以及双正交小波等,针对处理问题的不同可选用不同的小波函数。
1.2 Mallat算法
1986年S.Mallat和Y.Meyer提出了多分辨率分析概念,其思想是将原始信号分为不同分辨率上的几个信号,然后选择合适的分辨率或者在各级分辨率上处理此信号[2]。在多分辨率理论分析的基础上,S.Mallat引入了离散栅格上小波变换的快速算法,即Mallat算法,此算法被广泛应用于图像去噪领域。
把红外图像看成二维可分离信号,设矩阵Aj(l,k)为在空间分辨力2j上(j是分辨力索引,M≤j≤N,M、N为图像矩阵的大小)对原始图像Y的多分辨分析。根据Mallat算法,有:
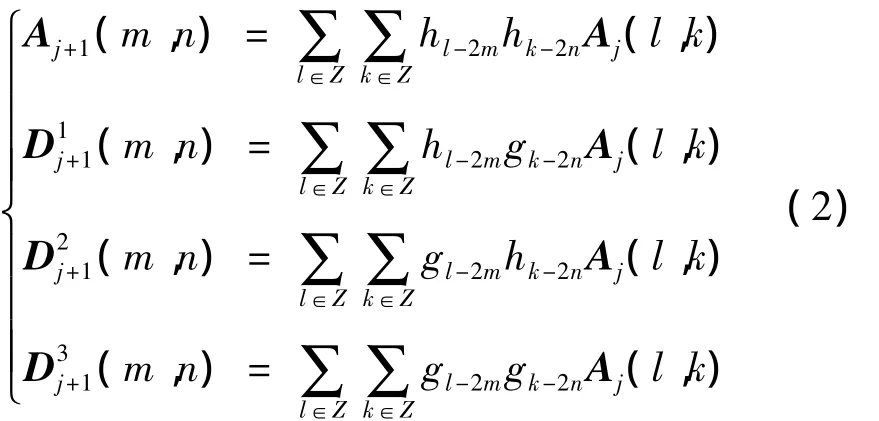
从图1表示的分解过程可以看出:二维图像的小波分解可以对图像依次按行、按列与一维的低通h和高通g滤波器作卷积来实现,在卷积之后进行相应的降2采样。二维图像的这种行、列可分离性简化了图像的小波变换,保证了图像处理的快速性。
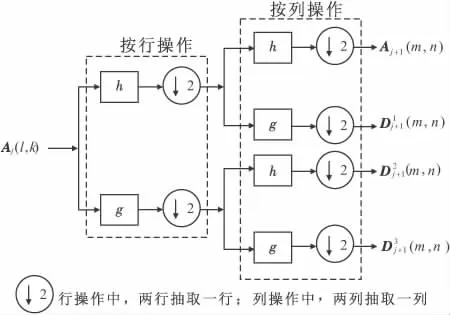
图1 二维Mallat算法分解过程
2 改进的小波阈值算法研究
近年来,基于小波变换的去噪方法层出不穷。Zhang提出的神经网络阈值函数法[3],通过一系列平滑非线性函数对小波系数进行解算,最终得到最佳阈值;Chang S G等人提出的一种BaresShrink去噪方法[4],具有很好的自适应特性,去噪效果好。文中结合空地导弹捕获目标的实时性要求选择实现简便、处理效果较好的阈值萎缩法对获取到的红外图像进行去噪。
2.1 阈值萎缩去噪方法
由于小波分解后能够将原始信号的能量集中到几个比较大的小波系数上,将噪声的能量分散到其他大量的小波系数上,因而噪声的小波系数比较小。通过设置合适的阈值算子λ削减这些较小的小波系数,同时保持较大的小波系数不变。常用的阈值函数为Donoho提出的软阈值(soft thresholding)和硬阈值(hard threshloding)函数。分别定义如下:
软阈值函数:
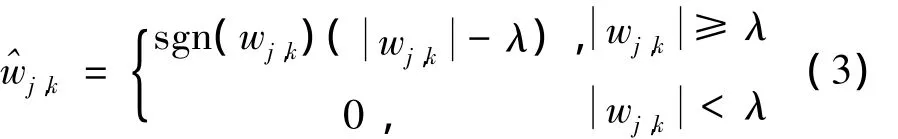
硬阈值函数:
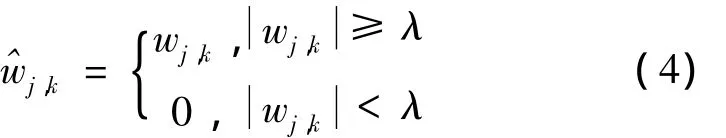
其对应的图像分别如图2(a)、图2(b)所示。
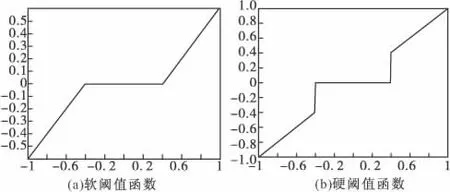
图2 两种函数的图形比较
从图2的对比中可以看出,软阈值函数整体连续性较好,处理效果相对平滑。但对阈值以外的信号进行了压缩处理,影响了重构后图像的逼近程度,造成边缘模糊等失真现象;硬阈值函数在阈值点处不连续,导致图像出现伪吉布斯效应等视觉失真。因此,有必要对阈值去噪方法加以改进。
2.2 阈值函数的改进
为了弥补传统阈值方法的不同,Sahraeian等人提出了一种基于指数函数形式的非线性滤波器[5],该方法既具有硬阈值函数刻画图像细节的性能,又具有软阈值函数平滑图像的处理效果。但该函数图像在阈值点处上升过快,曲线不平滑,导致图像出现振铃现象。
文中在此方法的基础上加以改进,构造了一种新的阈值函数,该函数在阈值点处趋近平滑,曲线近似连续,避免了图像产生振荡。阈值函数表示如下:
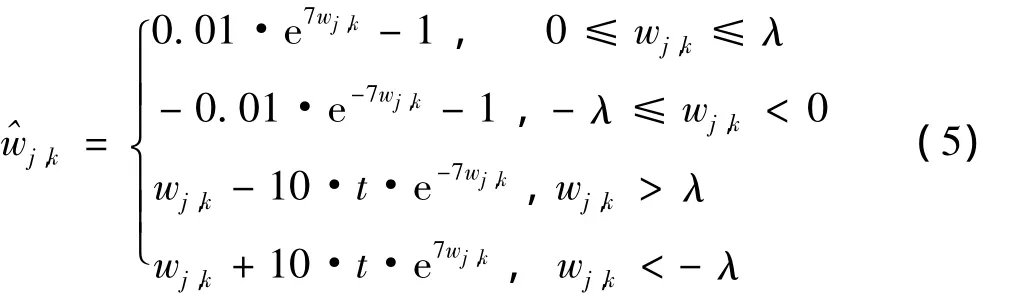
其中:t=0.1·(log(λ)+4.6)+0.1是此阈值函数的稳定因子,它对较大的阈值进行压缩以满足在任何情况下(阈值为任何值时)函数始终保持曲线平滑效果;式中的指数函数用来实现噪声区间与信号区间函数的平稳过渡,指数函数的幂越大,曲线曲率越大,反之幂越小,曲线越平滑。阈值函数图像如图3所示。
图3显示的是当阈值为0.5时的硬阈值函数、软阈值函数以及改进后的阈值函数。从比较中可以看出,改进后的阈值函数不仅具备软阈值函数的连续性,并且在阈值外更加逼近于硬阈值函数,能够保留更多的图像信息,保护图像边缘。在阈值附近的图像逼近平滑,避免了动荡图像的产生。
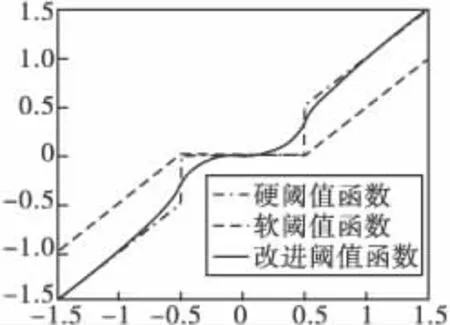
图3 阈值函数图像
2.3 新阈值的确定
阈值的选取是小波阈值去噪的中心问题之一,阈值选取的好坏直接影响到去噪效果。如果阈值选择过大,在去除噪声小波分量的同时,有用信号的一部分小波系数也会被去除,造成图像细节丢失[6];反之,如果阈值选择过小,就不会有效地去除噪声小波分量。
传统的阈值选取包括全局阈值、通用阈值以及BayesShrink阈值等[7]。全局阈值由Donoho 和Johnstone提出,是目前最常用的阈值,其表达式为:T为噪声标准方差,N为信号的尺寸长度。该方法运算简便,对一些要求不高的图像处理效果较好。事实上,小波变换将噪声从信号域压缩到小波域,这使得噪声方差随着小波分解级数的增多而基本不变,信号方差将会越来越大[8]。
将图像dam做1~5层小波分解,分别计算在每一分解级数上的信号方差、噪声方差以及噪声信号比率。其统计图如图4所示。
其中,横坐标为小波分解级数。从图中可以看出,随着小波分解级数的增加,信号方差不断变大,噪声方差几乎无变化,噪声在系数方差中的比例不断下降。在一级分解中子带所含近一半信息几乎被噪声淹没,随着分解级数的递增,到第5级分解,噪声在系数中的方差仅占0.15%。
基于以上现象,全局阈值无法适用于多级小波分解。因此需要对全局阈值加一权重因子,使其随着分解级数的增加阈值有所减小。设定:

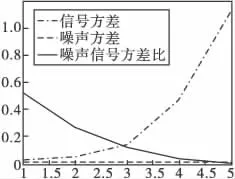
图4 方差统计图
其中:σ为噪声标准方差;N为信号的尺寸长度;j为小波分解级数;β为文中设定的权重因子,该权重因子使阈值随着噪声信号方差比的衰减而成比例的下降。
2.4 改进的小波阈值算法步骤
改进后的小波阈值算法步骤如图5所示。
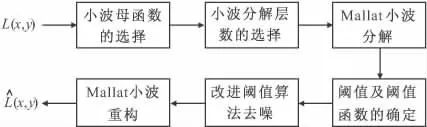
图5 改进后的算法步骤
具体处理步骤为:
1)选择合适的小波母函数及小波分解级数;
2)对航空武器获取到的红外图像利用Mallat算法进行小波分解;
3)运用式(5)~式(7)分别计算出阈值函数和阈值;
4)对分解出的高频小波系数运用改进的阈值函数进行去噪处理;
5)将处理后的小波系数运用Mallat小波重构算法进行重构,从而得到去噪后的红外图像。
3 实验结果与分析
基于db8母小波支集长度长、正则性好的特点[9],文中选用db8母小波对红外图像dam进行3级Mallat小波分解,并对分解后的高频小波系数进行改进后的阈值去噪处理。改进后的处理结果以及其他方法的处理结果如图6所示。

图6 图像去噪效果比较
从实验结果可以观察到:中值滤波与维纳滤波去除了图像中的部分噪声,但处理后的图像过于平滑,且丢失了部分细节;硬阈值法有效地去除了图像中大部分噪声,且较好的保持了图像边缘的细节特性,但图像出现了一些震荡;软阈值法的去噪效果虽然不及硬阈值法,但保持了图像的平滑特性;改进后的阈值算法去噪效果优于之前的算法,且较好的保留了图像细节信息,视觉效果清晰。
为进一步对以上5种算法的不同去噪效果做定量分析,建立评价体系结构,对其进行峰值信噪比(PSNR)的计算。计算公式为:

其中MSE是均方误差,表达式为:
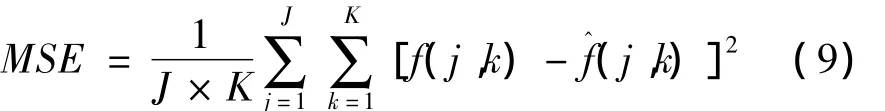

表1 不同图像去噪方法的峰值信噪比比较
从统计数据可以看到,采用改进后的阈值去噪方法得到的峰值信噪比明显大于其他算法,表明该算法在去噪方面具有明显的优势。
4 结论
针对航空武器在制导末段获取到的红外图像噪声较大的问题,提出运用小波变换的方法对红外图像进行去噪处理。文中在Donoho提出的小波阈值去噪算法基础上对阈值函数和阈值选取方法做了研究并加以改进,提出了一种新的小波阈值去噪算法,并将其应用于航空武器获取到的红外图像上。实验结果和实验数据表明改进后的算法在图像去噪方面具有明显的优势,并且保留了图像的细节信息,避免了振荡的产生。应用改进后的小波阈值算法对红外图像进行去噪处理有效地提高了航空武器末段精确打击的能力。
[1]占必超,吴一全.基于平稳小波变换和Retinex的红外图像增强算法[J].光学学报,2010,30(10):2788-2793.
[2]李晋炬,马志峰.基于旋转、平移和尺度不变的平稳小波图像去噪[J].激光与红外,2010,40(11):1263-1268.
[3]Xiao-Ping Zhang.Space-scale adaptive noise reduction in images based on thresholding neural network[C]//Proc.ICASSP,Salt Lake City.2001,5:1889-1892.
[4]Chang S G,Yu B,Veterli M.Spatially adaptive wavelet thresholding with context modeling for image denoising[J].IEEE Transactions on Image Processing,2000,9(9):1522-1531.
[5]S M E Sahraeian.Wavelet image denoising based on Improved thresholding neural network and cycle spinning[C]//IEEE International Conference on Acoustics,Speech and Signal Processing,2007:585-588.
[6]Khare A,Khare M,Jeong Y.Despeckling of medical ultrasound images using Daubechies complex wavelet transform[J].Signal Process,2010,90(2):428- 439.
[7]Bhuiyan M I H,Ahmad M O,Swamy M N S.Spatially adaptive thresholding in wavelet domain for speckling of ultrasound images[J].IET Image Proc.,2009,3(3):147-162.
[8]Han Jinku,Li Dahui.The application of estimation method based on improved wavelet coefficients[C]//International Conference on Multimedia Communications.IEEE Press,2010:175-178.
[9]段瑞玲.非线性阈值自调整小波图像去噪方法研究[J].光电子·激光,2006,17(7):871-874.

