基于误差分离的初始对准方法研究*
张 玲,赖际舟,刘建业,吕 品
(南京航空航天大学导航研究中心,南京 210016)
0 引言
初始对准技术是惯性技术研究的热点,使用高精度的初始对准方法也是重要的研究方向。目前,初始对准技术的研究主要集中在以下几个方面:静基座初始对准技术、动基座初始对准技术以及传递对准技术。
文中针对航向角误差较大的情况提出了一种新的对准方法。建立了新的姿态误差模型,通过对姿态误差中的航向误差和水平姿态角误差分步处理的方式,改进了初始对准算法,避免了航向误差对水平姿态角对准的影响,提高了对准的精度,改善了对准的性能,并可与静基座、动基座及传递对准等进行组合,起到更好的对准效果。
1 初始对准原理与分析
1.1 捷联惯导系统及坐标系模型
定义相关坐标系:惯性坐标系(i系),地球坐标系(e系),导航坐标系(n系),水平坐标系(h系)和机体坐标系(b系)。在地理坐标系里,速率矢量的表达式为:
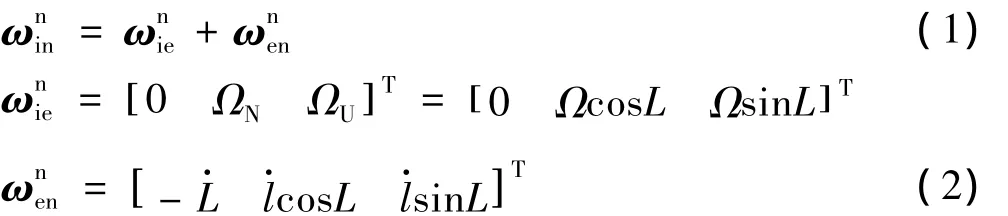
1.2 初始精对准原理分析
精对准的目的是:自动检测陀螺的漂移,精确的计算方位角,为导航计算提供准确的初始条件,以便正常地进行导航工作。由于单一固定位置对准时系统的可观测性矩阵不满秩,无法对所有状态进行估计,为了能对更多误差状态量进行估计,采用转动惯性测量单元的方式,获取不断变化的载体姿态,改善捷联惯导系统误差的可观测性[1]。
以最优多位置精对准为例,由于地理位置精确已知,忽略了位置误差,同时考虑惯导系统的垂直通道不稳定,所以只采用水平方向的速度误差和加速度计误差作为状态量,初始对准误差状态方程定为10阶。以北-东-地地理坐标系为导航坐标系,初始对准误差模型的状态方程为[2]:

式中:δVN、δVE为速度误差沿北、东方向的分量;φN、φE、φD为平台误差角在北、东、地方向的分量;∇x、∇y为水平加速度计的零偏;εx、εy、εz为三轴陀螺漂移;ωD=-ωiesinL为地球自转角速度在地向的投影分量;ωN=ωiecosL为地球自转角速度在北向的投影分量;g为当地重力加速度矢量的绝对值;Cij(i=1,2,3;j=1,2,3)为姿态转移矩阵中相应的元素,
将两个水平速度误差δVN、δVE作为卡尔曼滤波器的观测量,观测方程为:

其中,V是速度误差的观测噪声矢量,为高斯白噪声过程,服从正态分布。
具有代表性的最优多位置对准方法有:二位置方法与三位置方法。二位置对准中,当方位角改变180°时,方位失准角估计误差达到最小值,则确定该位置为初始对准的最优第二位置。三位置对准则是在二位置对准基础上,进一步减小等效天向陀螺漂移估计误差。当横滚角(或俯仰角)改变90°时,等效天向陀螺漂移估计误差达到最小值,因此将该位置作为初始对准的最优第三位置。根据参考文献[3-5]分析可知,最优多位置对准能有效提高方位失准角估计精度,且一定程度上能够改善惯性器件误差的估计精度,但对准所需的时间仍较长。
2 姿态角误差分离方案
2.1 姿态角误差分离算法研究
建立地理系与水平系的相对关系如图1所示。H坐标系是当地水平坐标系,绕地理系的纵轴做角度为航向角ψ的旋转。
姿态角(横滚γ、俯仰θ、航向ψ)中横滚角和俯仰角合称为水平角。将水平角和航向角分开考虑,得到机体系与导航系的坐标余弦矩阵包含两部分:

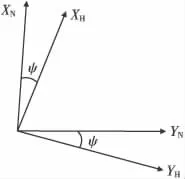
图1 地理系与水平系的关系
方向余弦矩阵的估计误差为:

当机体系与导航系之间的误差角为小量时,对三角函数取一阶近似,可以得到:

这里,δϑn=[δϑEδϑNδϑU]T是导航系下的小角度误差矢量。当航向角误差较大时,会引入较大的模型误差。此时,需要对姿态误差模型进行改进。
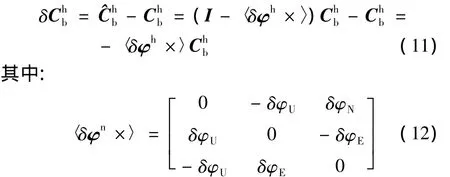
这里,δφn=[δφEδφNδφU]T是H坐标系下的小角度误差矢量。

将式(13)和式(14)代入式(9),得:
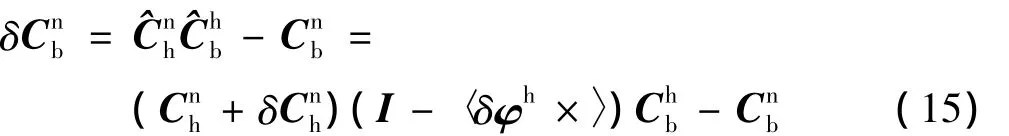

2.2 水平初始姿态角求解
当捷联惯导系统的陀螺仪误差较大且没有经过有效补偿时,方位角误差很大,此时可以用加速度计的信号代替陀螺的输出进行水平初始姿态角的计算,即矩阵的求解。
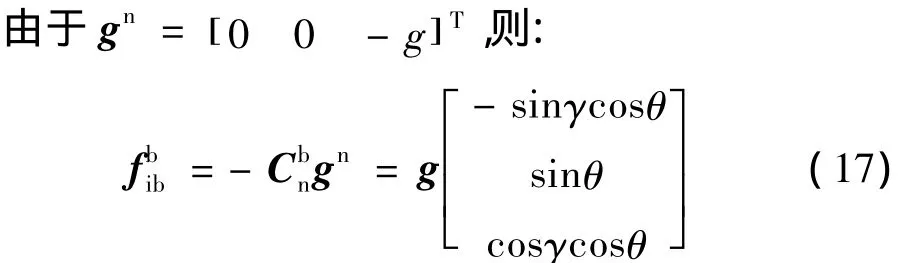
可以计算水平姿态角:
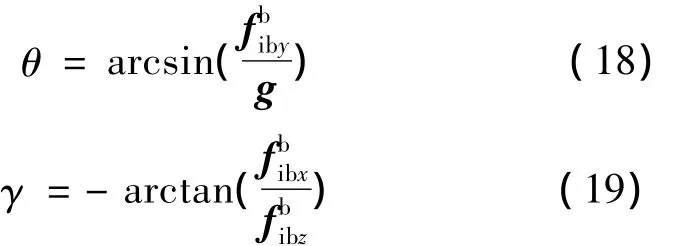
3 分离算法的仿真与分析
为了验证姿态角误差分离算法对系统性能的改善效果,文中建立了基于误差分离的惯导系统仿真平台,通过某型光纤陀螺与挠性加速度计构建IMU,在2TD-450双轴转台上进行模拟试验,采用姿态角误差分离算法对实测的数据进行分析。融合姿态角误差分离的捷联惯导解算原理图如图2所示。
IMU的性能参数为:光纤陀螺0.3°/h,加速度计0.0006g。IMU的运动模式设定为绕垂直轴做6°/s的旋转,在姿态解算时分为:水平角不变,航向角以6°/s的速度变化。经过姿态角误差分离算法的补偿,得到捷联惯导系统补偿前后的对比曲线如图3~图6所示。

图2 改进的捷联惯导解算原理图
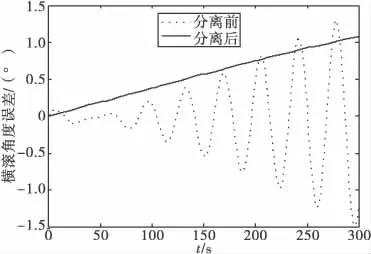
图3 横滚角误差

图4 俯仰角误差
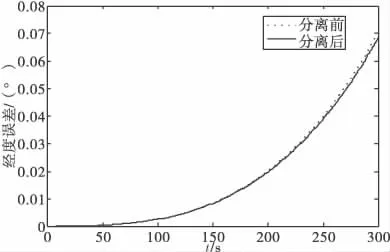
图5 经度误差

图6 纬度误差
分析图3~图6可知:
1)IMU在安装过程中存在非正交性误差,水平方向上的旋转角速率误差,使得横滚角和俯仰角误差出现震荡现象;
2)使用姿态角误差分离算法,横滚角和俯仰角不会因为IMU安装的非正交性而存在垂直旋转角速率的分量,图3和图4所示的水平姿态角误差不存在震荡误差,平稳性得到很好的改善;
3)姿态角误差分离算法对位置精度的改善不明显,分离前后的经度误差曲线基本趋于一致,如图5所示;纬度误差虽然有所改善,但是仍保持在10-4量级不变。
综合分析,在对准过程中使用姿态角误差分离方法,对水平姿态角的误差起到很好的改善作用。
4 结论
针对惯导系统初始航向角误差较大的问题,提出了一种新的误差分离方法。文中研究了姿态误差分离的算法,分析并推导了误差分离矩阵,建立了基于误差分离方法的惯导系统仿真平台。仿真实验结果表明,通过航向、水平姿态角的误差分离,有效避免了航向误差对水平姿态角的污染,该方法的研究对进一步提高初始对准的精度起到很好的推进作用,具有一定的理论研究价值。
[1]Goshen-Meskin D,Bar-Itzhack I Y.Unified Approach to Inertial Navigation System Error Modeling[J].Journal of Guidance,Control,and Dynamics,1992,15(3):648-653.
[2]万德均,房建成.惯性导航初始对准[M].南京:东南大学出版社,1998.
[3]蒋庆仙,马小辉,陈晓璧,等.光纤陀螺寻北仪的二位置寻北方案[J].中国惯性技术学报,2006,14(3):1-5.
[4]Chung D Y,Lee J G,Park C G,et al.Strapdown INS error model for multiposition alignment[J].IEEE Transactions on Aerospace and Electronic Systems,1996,32(4):1362-1366.
[5]Yu Fei,Ben Yue-yang,Li Qian,et al.Optimal two-position alignment for strapdown inertial navigation system[C]//Intelligent Computation Technology and Automation,2008 International Conference,2008:158-164.

