卡尔曼滤波在陀螺漂移时间序列模型中的应用*

张晓霞，曹咏弘

(中北大学理学院，太原 030051)

0 引言

随着 MEMS(micro-electro-mechanical system，微电子机械系统)技术的发展，MEMS陀螺已经步入了全面发展的阶段，基于MEMS惯性器件构建低成本的微型惯性导航系统也成为目前惯性技术领域的一个研究热点。

MEMS陀螺误差分为确定误差和随机误差两部分。其中确定误差可以通过测试和标定的方法进行补偿，而随机误差因为具有随机性，只能用统计模型来描述。近年来，使用时间序列分析法来建立随机误差模型，是提高微惯性导航系统精度的一种有效方法。文献[1]利用时间序列分析法对随机漂移建立ARMA模型，但并未给出检验。文献[2]采用时间序列分析法建立随机误差模型，然后基于该模型设计了卡尔曼滤波器，但文中在建立模型时，没有根据实测的数据进行分析而是从实践经验中选择模型。

基于以上的不足，文中同样采用时间序列分析法来建模并利用Matlab时间序列工具箱对模型参数进行估计并检验，最后设计了卡尔曼滤波器对其进行误差补偿。

1 时间序列分析与建模

1.1 数据的采集、预处理与检验

采集信号以得到观测数据，对该数据进行预处理并检验，以得到平稳、正态、零均值的时间序列，这是时间序列建模的基础。

1)数据采集。MEMS陀螺输出的实际数据是连续的，而建模要求是离散的，故要以一定的采样频率对其进行采集，得到离散序列 yk，k=1，2，…，350001。MEMS陀螺X轴的原始漂移信号见图1。

2)数据预处理。建模前，首先保证数据为零均值、平稳、正态。陀螺原始数据中的常值分量可以通过求均值来提取，但有时信号中还可能存在一定的趋势项，可以对其作一阶或几阶差分处理。提取均值并作一阶差分得到 xk，k=1，2，…，350000，xk=yk+1－ yk。

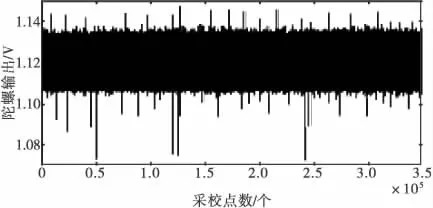
图1 MEMS陀螺X轴的原始漂移信号

3)数据检验。对其上述处理过的数据进行检验，以确定是否符合建模要求。通过统计检验的方法[3]对处理后的数据进行检验，是平稳、正态、零均值，符合建模要求。

1.2 模型的建立与参数的估计

1.2.1 模型的建立

自回归滑动平均模型(ARMA(p，q))的一般形式[3]：

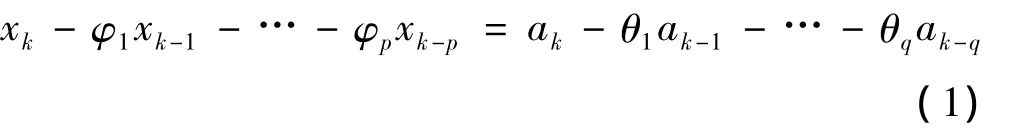
其中：xk为随机时间序列;p、q为自回归阶数和滑动平均阶数;φi(i=1，2，…，p )、θj(j=1，2，…，q)为自回归系数和滑动平均系数;ak为均值为零方差为的白噪声。式(1)中，如果q=0，则ARMA(p，q)退化为p阶自回归模型，记为 AR(p);如果 p=0，则ARMA(p，q)退化为q阶滑动平均模型，记为MA(q)。

模型的确定目前采用的主要方法有：相关特性(自相关函数和偏相关函数表现出不同的”截尾”和”拖尾”特性[4])、数理统计、信息准则等。在此采用相关特性和信息准则来确定MEMS陀螺的随机漂移模型。

由图2知：偏相关函数具有明显的拖尾现象。因此，模型可选MA模型或ARMA模型。

图2 自相关函数与偏相关函数

1.2.2 模型参数的估计

将ARMA(p，q)模型写成矩阵的形式：

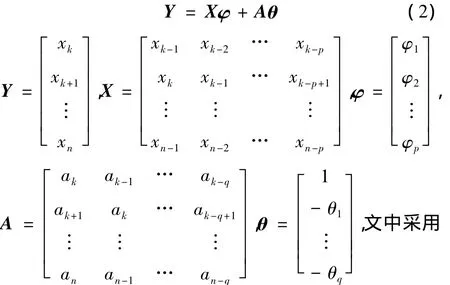
Yule-walker法[3]估计式(2)中的φ和θ，得到估计值

1.3 模型检验

陀螺随机漂移模型的阶次一般不会超过3阶。在此采用armax函数[5]来估计参数并求出AIC和FPE值，从MA和ARMA模型中选择AIC和FPE值最小的模型。所有模型及计算得到相应的准则值如表1所示。

表1 序列模型的定阶

由表1知，ARMA(2，2)的AIC和FPE值最小。因此选择ARMA(2，2)模型，表达式为：

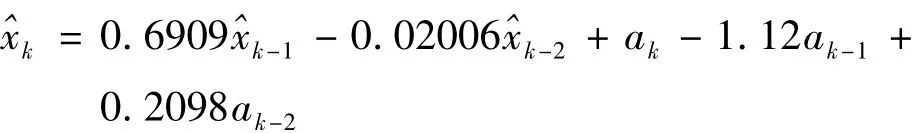
xk由yk经一阶差分得到，故MEMS陀螺随机漂移时间序列模型ARIMA(2，1，2)的表达式：

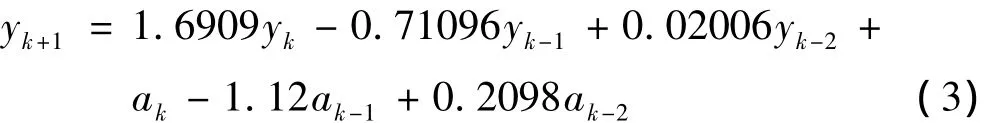
其中：yk+1为 ARIMA(2，1，2)模型的输出，即估计的时间序列，ak为白噪声。

2 基于ARIMA(2，1，2)模型的卡尔曼滤波

基于ARIMA(2，1，2)模型，利用传统的卡尔曼滤波算法来抑制误差，其表达式：

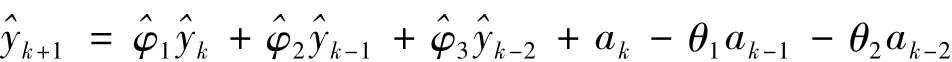
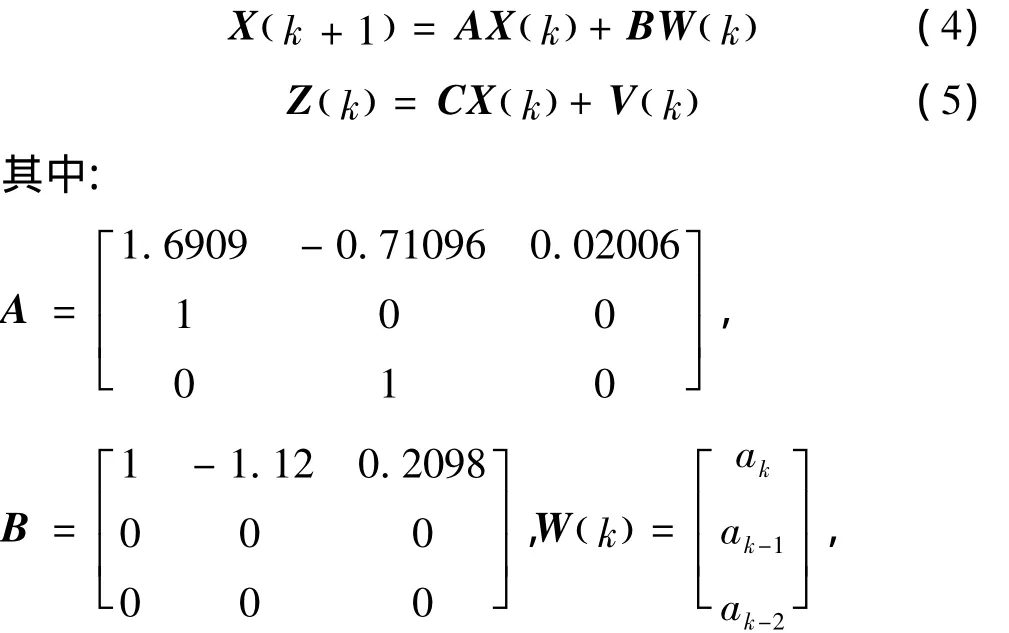
C=[ 1 0 0]。W和V分别为均值为零方差为Q和R的白噪声且互不相关。

卡尔曼滤波的递推方程[6]：

预测、估计误差方差阵分别为：

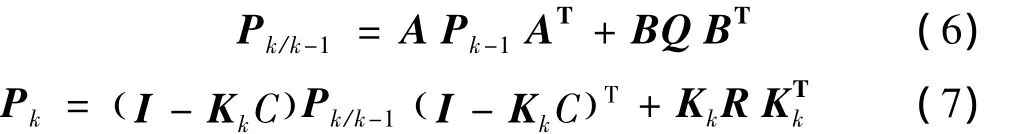
增益矩阵为：

预测、估计状态分别为：

卡尔曼滤波是一种递推算法，给定初始状态向量及误差方差阵，就可以通过上面的递推方程进行最优估计。

3 仿真实验

为了验证上述建立的时间序列模型及卡尔曼滤波算法的有效性，对某三轴MEMS陀螺实测数据进行仿真。取卡尔曼滤波初值为：X(0)=[ 0 0 0]T，P0/0为单位阵。仿真实验结果见图3～图5。同时也通过计算得到三轴数据滤波前后的均值和方差并进行了比较，如表2～表4所示。

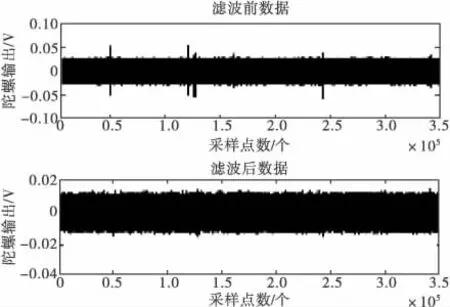
图3 MEMS陀螺X轴滤波前后对比图

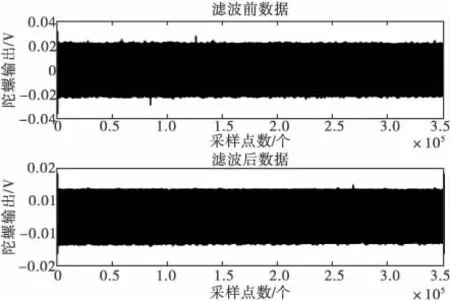
图4 MEMS陀螺Y轴滤波前后对比图

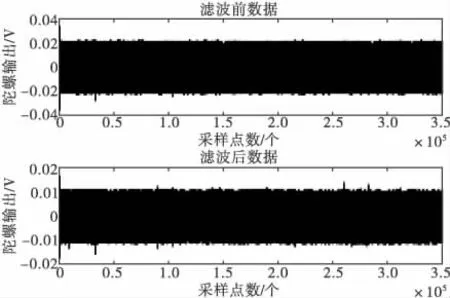
图5 MEMS陀螺Z轴滤波前后对比图

表2 MEMS陀螺X轴滤波前后数据比较

表3 MEMS陀螺Y轴滤波前后数据比较

表4 MEMS陀螺Z轴滤波前后数据比较

由图3～图5得：滤波前后曲线的变化规律没有改变，而噪声明显减小，滤波后的随机漂移至少减小了原来的50%。由表2～表4得：其均值在MEMS陀螺精度范围内可认为没有发生变化，但方差却比滤波前明显减小了一个数量级。仿真实验表明：建立的ARIMA模型及卡尔曼滤波器有效减小了随机误差，明显降低了随机漂移，从而提高了陀螺精度。

4 结论

提出了一种MEMS陀螺随机漂移误差的有效补偿方法。采用时间序列分析的方法对MEMS陀螺随机漂移动态信号数据建立ARIMA模型，运用Matlab函数对参数进行估计，并基于该模型设计了卡尔曼滤波器对其进行误差补偿。最后对实测的MEMS陀螺数据进行仿真实验，结果表明：建立的模型和卡尔曼滤波算法有效的减小了随机误差，明显的降低了随机漂移，从而提高了导航精度。

[1]王栋，万宝琳.微机械陀螺随机漂移误差分析与建模[J].中国水运，2008，8(11)：147－148.

[2]李杰，张文栋，刘俊.基于时间序列分析的Kalman滤波方法在MEMS陀螺仪随机漂移误差补偿中的应用研究[J].传感技术学报，2006，19(5)：2215－2219.

[3]杨叔子，吴雅，轩建平.时间序列分析的工程应用[M].2版.武汉：华中理工大学出版社，2007.

[4]于宁莉，易东云，涂先勤.时间序列中自相关与偏相关函数分析[J].数学理论与应用，2007，27(1)：54－57.

[5]曹鲜花，吴美平，胡小平.MATLAB在光纤陀螺随机漂移建模中的应用[J].航天控制，2007，25(1)：18－20.

[6]王志贤.最优状态估计与系统辨识[M].西安：西北工业大学出版社，2004.