小型察打无人机投弹非稳态干扰下六自由度仿真*

龚军锋，祝小平，周 洲

(1西北工业大学航空学院，西安 710072;2西北工业大学无人机研究所，西安 710065)

0 引言

小型察打无人机总重轻，携带的战斗部杀伤威力有限，对制导精度有很高的要求。无人机稳定性和机动性要满足控制和导引精度要求，特别是在受到机弹分离的非稳态气动力干扰影响下，要能够快速消除干扰所造成的姿态扰动。小型察打无人机的武器质量占全机比重比较高，投弹前后无人机整体的转动惯量发生了比较大的变化，对无人机的纵向和横航向稳定性都有影响，其挂弹位置、投射顺序等对无人机平台的飞行安全造成了严重影响。

进行载机投弹状态飞行力学仿真时，机弹分离的流场其非稳态气动力干扰难以用一套工程上可表达的方式建模。文中拟采用CFD技术求解物体运动的非定常流场获得实时气动力数据，进行飞行力学仿真。该建模方法特别适合这种察打无人机存在机弹干扰，有精确制导需求而气动干扰力复杂又要求精确的仿真。

1 基于CFD的非稳态气动干扰力

采用适用于移动边界的非结构网格非定常流场的计算方法，耦合外挂武器刚体六自由度运动学、动力学方程，求解出外挂武器的运动轨迹及姿态。同时非定常流场给出无人机的实时气动力，与稳态的气动力相减，给出外挂武器分离所带来的时间历程非稳态气动干扰力。

1.1 非结构动态网格及控制方程

近年来，最新发展起来的非结构动网格计算技术为计算机弹分离之类复杂相对运动造成的时变流场等领域提供了实际可行的工程方法。非结构动态网格迭代法的网格更新方法主要有弹簧光顺模型和局部重构模型[1－2]。

控制方程采用基于动网格的守恒型三维可压缩非定常N-S方程，其积分形式为：

图1 CFD计算网格

其中：Q=[ρ，ρu，ρv，ρw，e]T;F 为通量项，它包括无粘项FE和粘性项FV两部分：

理想气体的状态方程为：

与常规的N-S方程相比，对流项采用相对速度代替了流体对流速度。对时间的导数由偏导改为全导，即要考虑控制单元的体积随时间的变化。基于动网格的N-S方程的雷诺平均与以往的RANS具有相同的形式和雷诺应力项。层流粘性系数由Sutherland公式给出，应用Boussinesq假设，湍流粘性系数由湍流模型给出。湍流模型采用S-A湍流模型，近壁处理采用壁面函数法。

采用有限体积法进行计算区域及控制方程的离散。非定常时间推进采用双时间的积分形式。

1.2 外挂武器六自由度运动方程

忽略外挂武器投放运动过程中自身的变形，作为刚体考虑。计算运动刚体上的气动力、重力以及其它外力，求解运动的牛顿－欧拉方程得到运动刚体的新的位置和姿态，并更新流场网格进行下一时间步的计算。刚体的姿态采用3个欧拉角描述，俯仰θ、偏航ψ、滚转φ。

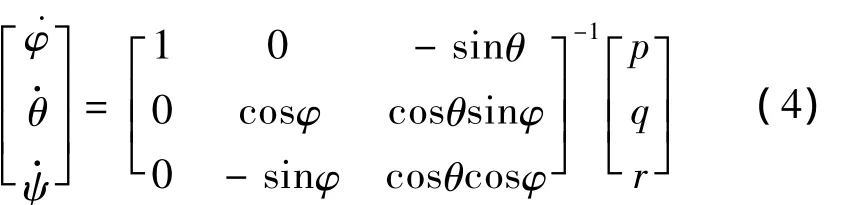
图2 耦合求解流程图

先以分离前的定常流场计算结果作为初始流场。当每一时间步流场计算完成，积分出分离弹体上的气动力和力距。将气动力、力距和外力模型给出的力诸如重力、弹射力、发动机推力等叠加，然后输入到弹体六自由度动力学模型中。在六自由度动力学模块中给出弹体下一时刻的位置、姿态和速度等信息，弹体位置、姿态信息传给网格划分模块。网格划分模块更新流场网格，然后进行下一轮的迭代计算。以此类推。

2 载机的六自由度仿真模型

2.1 六自由度动力学及运动学方程

文中采用建立在机体坐标轴下的载机六自由度动力学方程[3－4]。下式为机体轴系绕质心转动动力学方程，不同于一般的面对称飞行器，式中的惯性积Ixy≠0、Iyz≠ 0。

2.2 六自由度动力学及运动学方程

巡航阶段的控制率在察打无人机武器投放阶段起控制作用，通过调整升降舵、副翼、方向舵以及发动机动力来控制无人机的姿态、速度和高度[5]。飞行控制系统的舵回路一般可等效为一个一阶惯性环节。

其中：kδ为舵回路的静态增益;Tδ为时间常数。实际含舵机控制系统存在的惯性主要来自舵回路，文中Tδ=0.1s。

2.3 投弹前后仿真模型的变化

除了无人机投弹后的时间历程非稳态气动干扰力由CFD给出外，投弹前后无人机的状态发生了以下突变：稳态的气动力数学模型发生变化，主要是无人机的全机状态发生了变化，气动特性数据需要由挂弹状态改为投弹后状态。投弹后，无人机的重量、重心位置、转动惯量都发生了变化。

2.4 非线性仿真模型的建立

在带弹的稳态气动力状态下，进行稳定飞行的配平及仿真。在机弹分离的一瞬间，稳态气动力数据更新为投弹后的状态，并同时更新无人机质量、转动惯量特性。CFD求解器对无人机机体进行气动力积分，给出机体气动力在分离过程中的实时气动力，然后与投弹后的稳态气动力求差，给出非稳态干扰气动力。将该非稳态气动力作用于无人机六自由度模型，仿真求解给出无人机的动态响应。

图3 仿真系统框图

3 仿真结果及分析

3.1 机弹分离过程

采用CFD求解技术计算了机弹分离的非定常流场，给出机弹分离的动态过程中弹体的运动参数以及流场的压力分布，积分给出载机所承受的气动力。

图3、图4给出机弹分离过程的弹体轨迹及姿态的时间历程变化。由图可以看出，由于存在重力方向的运动，使气流相对弹体存在正攻角，在稳定翼面的作用下，弹体的俯仰角越来越大。

图4 轨迹曲线

图5 不同挂弹位置机弹分离三维轨迹图(Δt=0.05s)

3.2 非稳态干扰气动力

根据上述方法，图5给出了距对称面1m、2m及3m的单边投放的CFD数值模拟流场作用于载机的非稳态干扰气动力。

图6 时间历程非稳态干扰气动力

由图6可以看出非稳态干扰气动力在前0.5s变化比较剧烈，0.5s后逐渐平稳的向零收敛。在3个方向的干扰力和力矩中载机的侧向力量值最小。距离机身最远的挂弹位置，干扰力没有意料中的大，而且很快的衰减。从气动干扰来讲，挂弹位置离机身越远越好。

3.3 载机的动态响应

在载机的动态响应仿真前，首先进行了投弹前巡航状态的配平。在载机的稳定状态基础上，进行投弹过程载机的动态响应仿真。

3.3.1 不同挂载位置的载机动态响应

在机翼上挂弹越远离对称面，对转动惯量及干扰力矩的影响越大。文中对距对称面3个位置的单边投放情况载机的动态响应进行了仿真。

挂弹展向位置的变化对纵向气动特性的影响不大，载机动态响应的变化主要体现在横航向上。挂弹位置越靠近翼尖，对方向舵，特别是副翼的用舵量变大，载机的滚转角也越大。采用该仿真方法能给出载机动态响应，方便对挂弹方案进行评估。

3.3.2 不同投放间隔的载机动态响应

以某无人机机翼左右各挂一枚制导炸弹为例分析：投弹前的状态为构型一、左侧的武器投放后为构型二、左右武器都投放后为构型三。文中对左右投弹的不同投放间隔的载机动态响应进行了仿真，分别为单边投放、同时投放、间隔2s至0.1s不等。

图7 不同挂载位置投放的载机动态响应

图8 不同投放间隔的载机动态响应

由图8仿真结果可以看出左右投放越接近，对横航向的扰动越小，但随即对纵向的扰动变大。由于文中的挂载方案远离临界边界，所以载机动态响应比较小，对安全性的影响不大。当挂载方案接近临界边界，就需要综合纵/横航向扰动情况对投放间隔给出约束条件。

由于文中的研究目的是建立对该类问题的研究方法，为了研究方便，只考虑了自由投放的气动干扰力，研究对象没有考虑弹射投放的弹射力以及挂架发射的后座力、摩擦力以及喷流的干扰。但这些因素可以很容易的反映到本文建立的模型中。

4 结论

文中采用CFD技术求解机弹分离的非定常流场，获得实时非稳态干扰气动力数据。考虑投弹前后无人机的状态突变及非稳态干扰气动力，建立了察打无人机投弹六自由度的仿真平台。通过该仿真平台可以分析不同挂弹位置及投放间隔等挂弹方案对察打无人机平台的安全性影响，并指导方案设计。

[1]Farhat C，Degand C，Koobus B，et al.An improved method of spring analogy for dynamic unstructured fluid meshes，AIAA 98－2070[R].1998.

[2]Lohner R，Baum J D.Three-dimensional store separation using a finite element solver andadaptive remeshing，AIAA 91－0602[R].1991.

[3]胡兆丰，何值岱，高浩.飞行动力学——飞机的稳定性与操纵性[M].北京：国防工业出版社，1985.

[4]方振平，陈万春，张曙光.航空飞行器飞行动力学[M].北京：北京航空航天大学出版社，2005.

[5]张明廉.飞行控制系统[M].北京：航空工业出版社，1993.