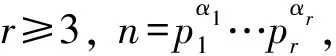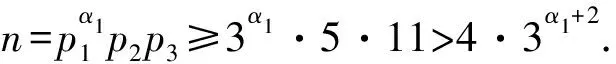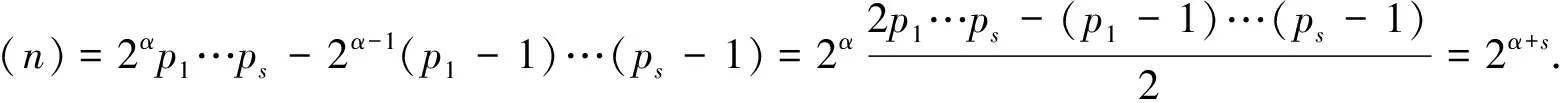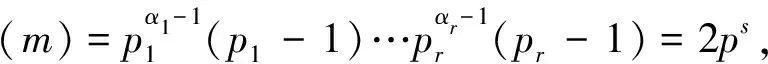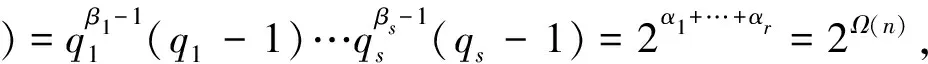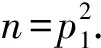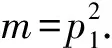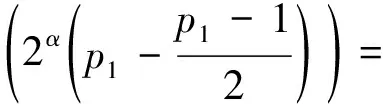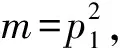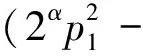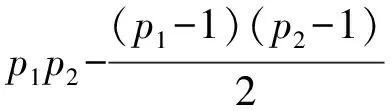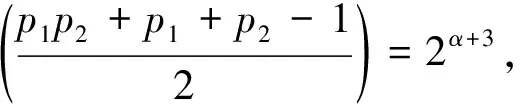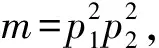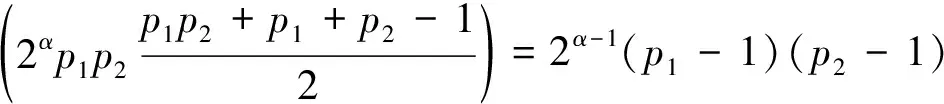若干包含Euler函数φ(n)的方程

孙翠芳, 程 智

(安徽师范大学 数学计算机科学学院, 安徽 芜湖 241000)

Ω(1)=0,Ω(n)=α1+…+αr.

本文将对三类方程n-φ(n)=2Ω(n),n-φ(φ(n))=2Ω(n)和φ(n-φ(n))=2Ω(n)正整数解的情况进行研究, 给出了它们所有的正整数解. 所得结果不仅给出了部分非φ值和非对偶φ值, 而且利用数论函数Ω(n)对正整数n与φ(n)差的情况做了相应刻划.

引理1[9]对任意正整数m和n, 若mn, 则φ(m)φ(n).

引理2[9]若q=2l+1是一个素数, 则有非负整数k, 使得l=2k.

素数q=22k+1称为Fermat素数.

引理3设s是大于1的整数, 若qi=22ki+1(i=1,2,…,s)是不同的Fermat素数, 2k1+…+2ks=r, 则q1q2…qs<(220+1)r=3r.

证明: 由于qi(i=1,2,…,s)是不同的Fermat素数, 所以不妨设q1

证明: 当r=3时, 若α2≥2或α3≥2, 则有

当r≥4时, 有

所以当r≥3时, 结论成立.

引理5若r≥3,n=p1…pr, 其中p1,…,pr是不同的奇素数, 则n-φ(n)>2·3r.

证明: 对r使用数学归纳法, 若r=3, 则

假设结论对r成立, 即有p1p2…pr-(p1-1)(p2-1)…(pr-1)>2·3r成立, 则对r+1的情形, 有

由归纳法知结论成立.

证明: 当r≥3,s≥1时, 由引理5, 有

定理1方程n-φ(n)=2Ω(n)的所有正整数解是n=2α·3, 其中α是正整数.

证明: 方程n-φ(n)=2Ω(n)显然没有奇数解. 设n是方程n-φ(n)=2Ω(n)的偶数解, 令n=2αm, 其中:α是正整数;m是奇数.

即s=1,p1=3, 且n=2α·3, 其中α是正整数. 证毕.

定理2方程n-φ(φ(n))=2Ω(n)的所有正整数解是n=3.

证明: 方程n-φ(φ(n))=2Ω(n)的奇数解显然只有n=3. 设n是方程n-φ(φ(n))=2Ω(n)的偶数解, 令n=2αm, 其中:α是正整数;m是奇数.

如果m=1, 则n=2α=2Ω(n), 且φ(φ(n))≥1, 因而n=2α不是方程n-φ(φ(n))=2Ω(n)的解. 如果m>1是奇数, 则φ(m)是偶数, 于是设φ(m)=2βt, 其中:β是正整数;t是奇数. 从而有

即2m-φ(φ(m))=21+Ω(m)及4⫮φ(φ(m)), 从而φ(m)=1,2,4,ps,2ps, 其中:p≡3(mod 4)是奇素数;s是正整数.

即r=1,α1=s+1,p=p1=3, 从而m=3s+1且

2m-φ(φ(m))=2·3s+1-2·3s-1=24·3s-1≠21+s+1=21+Ω(m),

故方程n-φ(φ(n))=2Ω(n)在这种情况下没有解. 证毕.

定理3方程φ(n-φ(n))=2Ω(n)的所有正整数解是n=2α·7,2α·11,2α·52,2α·3·7,52, 其中α是正整数.

即β1=…=βs=1,qi-1=2li,l1+…+ls=α1+…+αr, 根据引理2,q1,…,qs都是Fermat素数. 当r≥3时, 根据引理3,n-φ(n)=q1…qs<3α1+…+αs, 根据引理5及引理6,n-φ(n)>2·3α1+…+αr, 矛盾, 从而方程φ(n-φ(n))=2Ω(n)无解.

φ(n-φ(n))=φ(p1+p2-1)=4,p1+p2-1=5,8,2·5,22·3,

p1(p1+p2-1)=n-φ(n)=(220+1)(221+1)=3·5,

p1p2(p1+p2-1)=n-φ(n)=222+1=17,

所以方程无解.

如果r≥3, 若m=3α1·5·7,n=2α·3α1·5·7, 此时n不是方程的解, 所以m≠3α1·5·7, 由引理4～引理6知

2m-φ(m)=m-φ(m)+m>2·3Ω(m)+4·3Ω(m)=2·3Ω(m)+1.

即β1=…=βt=1, 并有正整数ki, 使得qi=22ki+1是Fermat素数, 2k1+…+2kt=Ω(m)+1.

由引理3知2m-φ(m)=2q1…qt<2·3Ω(m)+1, 矛盾, 所以方程在这种情况下无解.

即p1=5, 于是n=2α·52.

即

[1] Ford K, Luca F, Pomerance C. Common Values of the Arithmetic Functionsφandσ[J]. Bull London Math Soc, 2010, 42(3): 478-488.

[2] Makowski A. On Some Equationφ(n+k)=2φ(n) [J]. Elem Math, 1974, 29: 13.

[3] Nathanson M B. Elementary Methods in Number Theory [M]. New York: Springer-Verlag, 1999.

[4] Carmichael R D. Note on Euler Functionφ(n) [J]. Bull Amer Math Soc, 1922, 28: 109-110.

[5] Erdös P. On the Normal Number of Prime Factors ofp-1 and Some Related Problems Concerning Euler Functionφ(n) [J]. Quart J Math, 1935, 6(1): 205-213.

[6] Woolridge K. Values Taken Many Times by Euler Functionφ(n) [J]. Proc Amer Math Soc, 1979, 76(2): 229-234.

[7] Guy R K. Unsolved Problem in Number Theory [M]. 3rd ed. New York: Springer-Verlag, 2004.

[8] Maire H, Pomerance C. On the Number of Distinct Values of Euler’sφ-Function [J]. Acta Arith, 1988, 49: 263-275.

[9] Rosen K H. Elementary Number Theory and Its Applications [M]. 5th ed. Boston: Addison Wesley, 2005.