风电系统参数对Hopf分岔影响的仿真

李 季, 周雪松, 马幼捷, 王海洋

(1. 天津大学 电气与自动化工程学院, 天津 300072；2. 天津理工大学 天津市复杂系统控制理论及应用重点实验室, 天津 300384; 3. 白城师范学院 机械工程学院, 吉林 白城 137000)

随着风力发电风电容量的迅速增加, 风电并网对系统的影响日益显著, 但风电大规模接入电网会导致电能质量下降、 线路传输功率越限、 系统短路容量增加和暂态稳定性变化等问题[1-3]. 文献[4]指出风速变化会影响并网风电系统的电能质量, 引起系统电压的波动； 文献[5]指出风电机组对风电系统电压的影响程度决定于电网结构强度和风机容量大小.

风电的大规模接入必然会使系统运行点向稳定极限点靠近, 一对共轭特征根出现于虚轴而产生的Hopf分岔是该特征的一种现象. Hopf分岔是常见的分岔现象[6], 是导致电压失稳的3种分岔形式之一[7]. 分岔理论已成功解释了DAE(differential algebraic equation)方程所表示的非线性动态电力系统电压失稳机理[8-10]. 文献[11]研究了含风电场的电力系统静态电压稳定问题； 文献[12]基于延拓法追踪了基于风电系统静态模型的二维参数分岔边界. 但已有研究很少涉及风电系统DAE方程的Hopf分岔. 本文应用延拓算法追踪风电系统的平衡解曲线及两参数Hopf分岔边界, 分析参数对风电系统电压稳定性的影响, 并研究静止无功补偿器(static var compensation, SVC)对Hopf分岔的控制作用.

1 延拓算法

对于动力学系统[13]

(1)

其中：x表示状态变量；λ表示分岔参数.

设式(1)在平衡点(x,λ)出现Hopf分岔, 则该系统的Jacobi矩阵A=∂f/∂x在平衡点处有一对共轭纯虚根, 记为jω[13]. 对Hopf分岔, 有

f(x,λ)=0,Aq=jωq, 〈q,q0〉=1,

(2)

式(2)为复数, 即向量q和q0,x,λ,q,ω为方程的未知数, 方程的个数与未知数个数相等.

设式(1)的平衡点方程为f(x,λ)=0, 则该方程在n+1维的空间y=(x,λ)∈Rn×R1中定义了一个一维流形M, 称为平衡解曲线或平衡解流形, 延拓算法可追踪该平衡解流形, 即用一系列离散点(y1,y2,…)逼近曲线M, 该离散点满足平衡点的要求. 追踪该平衡流形的过程中, 通过检测局部分岔条件判断在该流形上是否存在分岔点. 但一般的延拓法仅能追踪到一维流形, 因此只能计算单参数分岔值. 为了实现微分代数方程表示的风电系统二维参数分岔边界的追踪. 可从单参数分岔点出发, 假设已追踪得到式(1)的单参数分岔点, 据此可探索将延拓算法应用到求解直接算法所能求解的数学方程中. 即等价于应用延拓算法追踪局部分岔满足的流形, 并非上述意义下的平衡解流形, 这时可求得式(1)的二维参数局部分岔边界.

2 风电系统模型

风电系统模型如图1所示. 该模型由2个发电机和1个风电场组成, 发电机G1为无穷大电源.

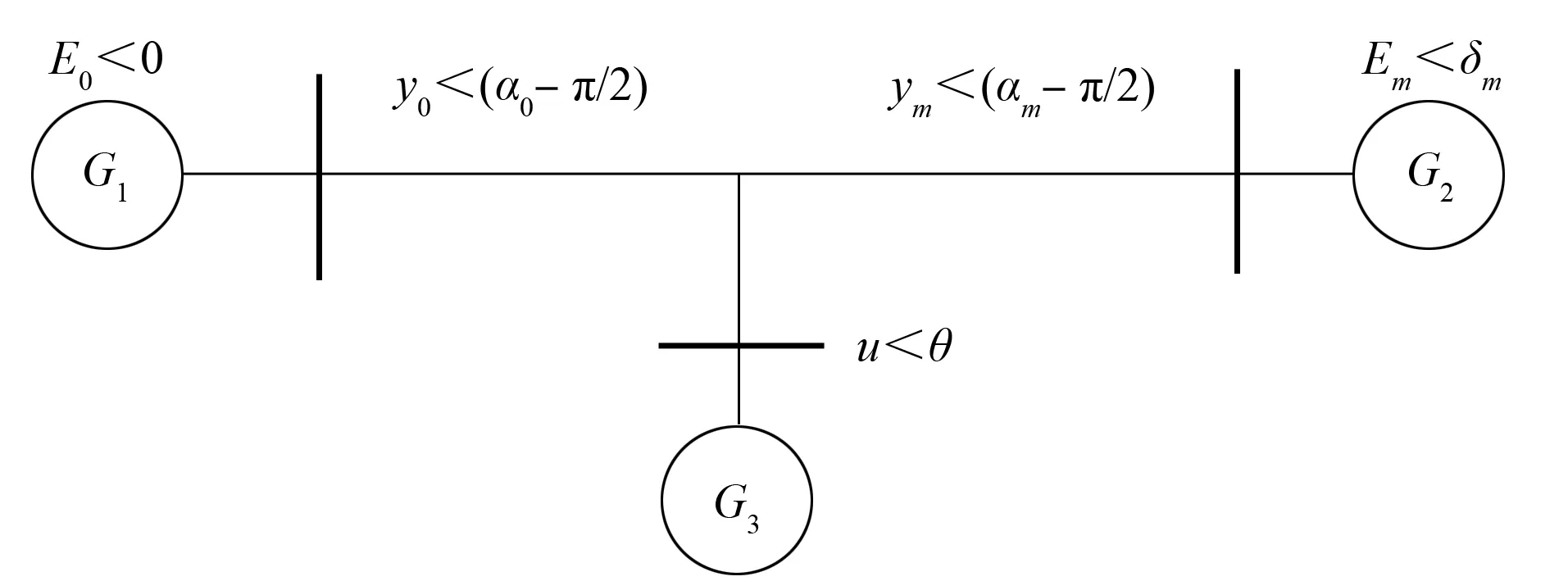
图1 风电系统模型Fig.1 Model of wind power system

2.1 等值发电机模型

等值发电机G2采用下述二阶模型:

其中：Em,M,Tm和Dm分别表示发电机机端电压、 发电机的惯量、 输入转矩及阻尼系数；ω和δm分别表示发电机角频率和发电机功角；ym和am表示网络参数.

2.2 风电场模型

异步发电机技术较成熟、 性价比高、 运行可靠, 是目前多数风电场的主流机型[14], 异步发电机运行时发出有功功率, 同时吸收无功功率, 使整个风电场对无功功率需求较大, 降低了风电接入地区电网的电压稳定性.

异步发电机采用忽略定子磁通暂态过程, 考虑转子绕组暂态过程的暂态模型.

1) 定子电压方程为

u=(r1+jx′)Is+E′.

(3)

2) 电磁暂态方程为

(4)

3) 转子运动方程为

(5)

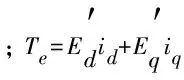
3 风电系统参数对Hopf分岔的影响

3.1 有功功率和无功功率对Hopf分岔的影响

Hopf分岔是最具代表性的动态分岔, 也是其他动态分岔的基础. Hopf分岔和电力系统的参数密切相关, 不同参数对Hopf分岔的影响也不同. 下面针对几个风电系统的典型参数对Hopf分岔影响进行分析.

由于风速的随机性和不确定性, 感应发电机消耗或吸收的无功功率也会不断变化, 导致电网电压的波动, 引起风电发电机组机端电压下降, 因而极大降低了系统电压的稳定水平. 以风电场吸收的无功功率Q1作为分岔参数时, 风电场机端电压u的Hopf分岔曲线如图2所示, 本文仅分析稳定平衡态的上半分支. 当无功功率Q1逐渐增加时, 风电场电压u快速降落, 在系统运行到极限点(limit point, LP)前的某时刻,Q1约达到1.499 884, 风电系统发生了Hopf分岔, 此时电压u=0.908 584, 如图2中的H1, Hopf分岔理论指出, 当系统发生Hopf分岔时, 系统出现振荡, 进而维持周期性振荡或振幅不断增大而导致最终失稳, 因此风电场消耗的无功功率将影响风电系统动态电压的稳定性.

风速的不断变化导致感应风电机组在运行中有功功率和无功功率同时变化, 二者相互影响, 因此针对风电场的两参数Hopf分岔分析更有意义. 如图3所示,P1和Q1为分岔参数风电系统电压u的二维Hopf分岔边界, 随着风电机组发出有功功率P1的增加, 其所吸收的无功功率Q1也会相应增加, 此时系统电压u下降. 由图2可见, 风电系统无功功率的增加易导致Hopf分岔发生, 所以图3给出了避免Hopf分岔发生, 提高电压稳定性的规律, 即随着风电场发出有功功率的增大, 必须减小风电场吸收的无功功率. 相应地, 如果风电场的无功功率增加, 则必须减少风电场的有功功率, 这样虽有效避免了系统运行在Hopf的二维分岔边界点上, 但Hopf分岔的消失以牺牲风电场的有功功率为代价. 所以控制风电场所吸收的无功功率是提高系统电压稳定性的一种有效方式.

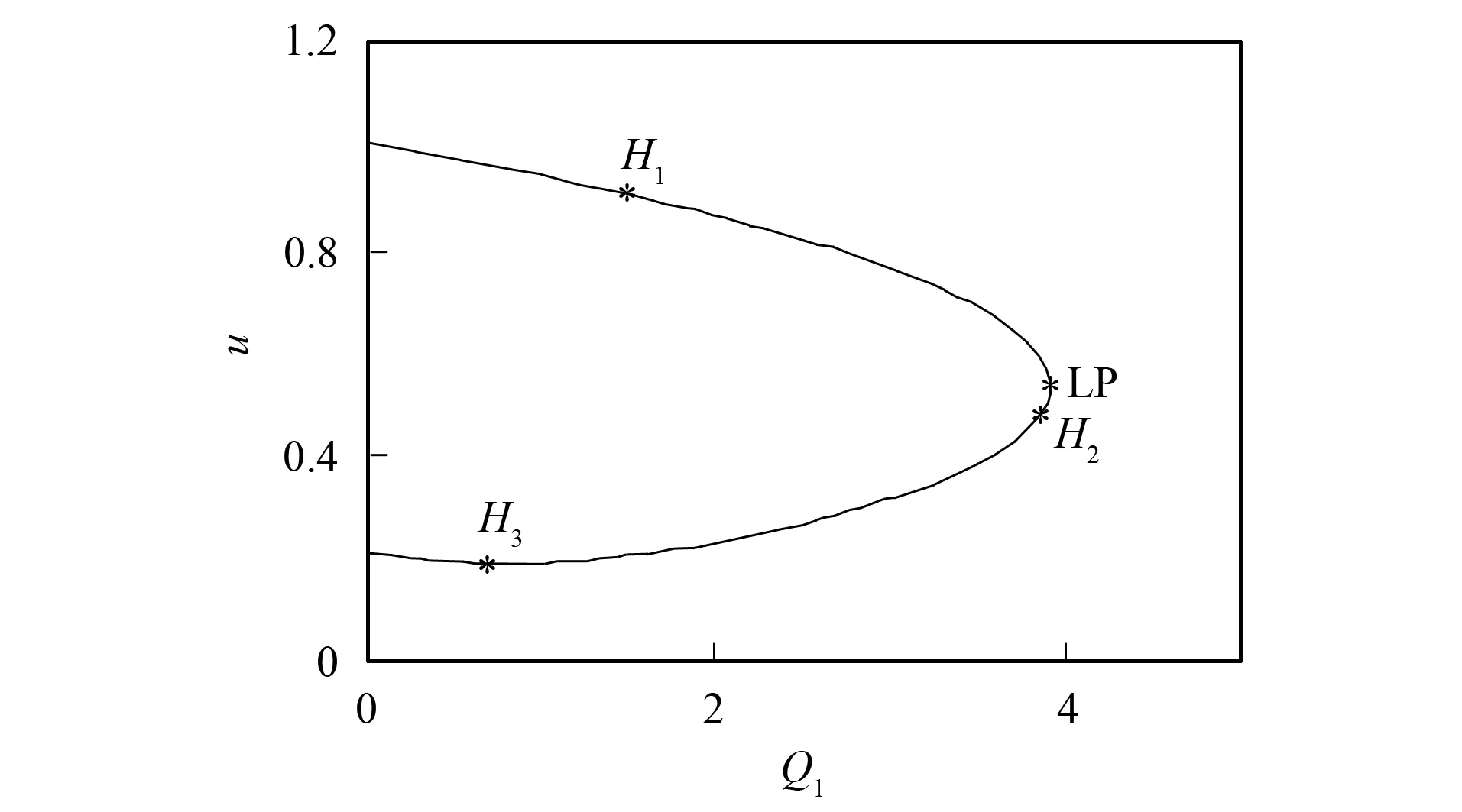
图2 Q1变化时风电系统的Hopf分岔曲线Fig.2 Hopf bifurcation curve of wind power system with Q1 variation

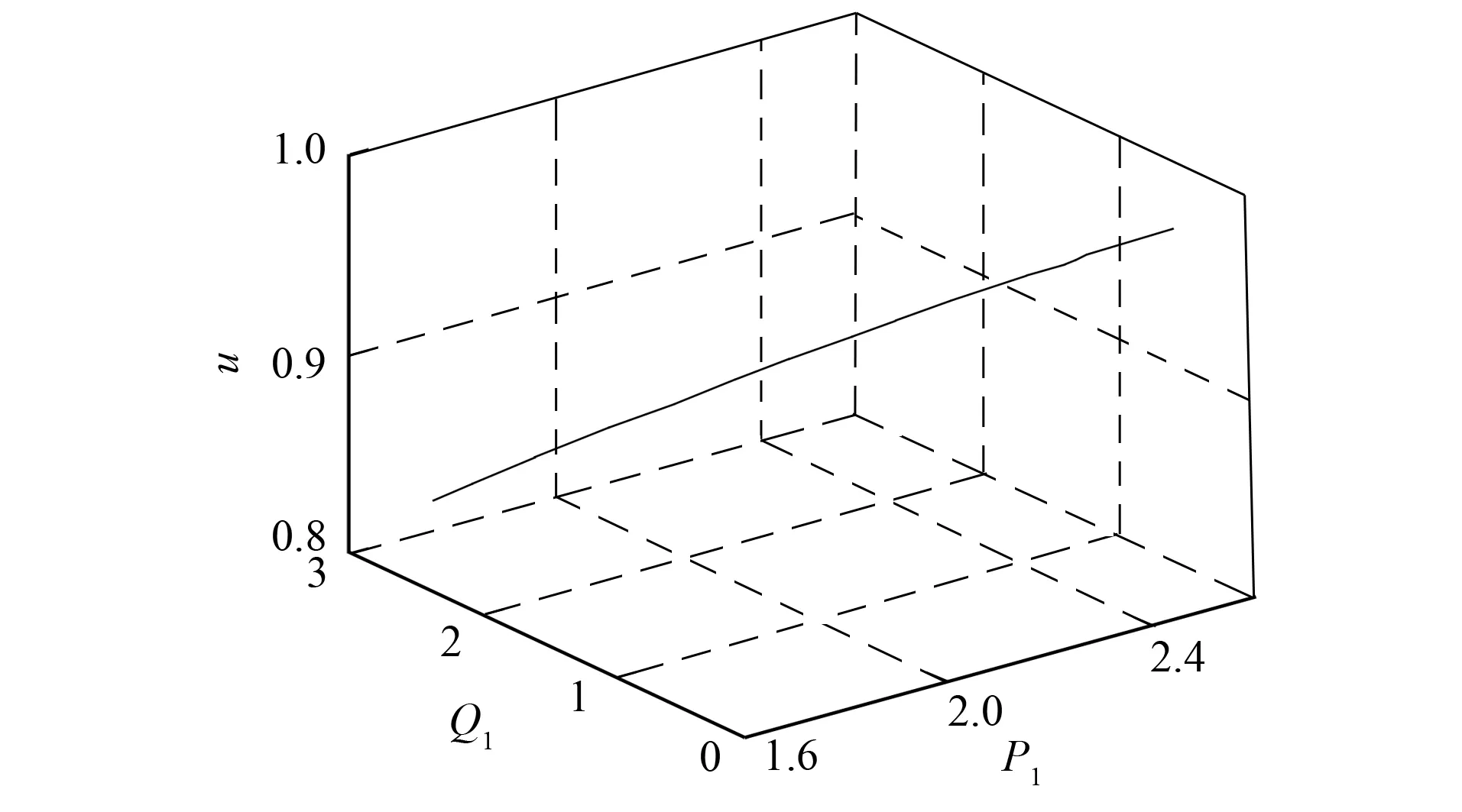
图3 P1-Q1的二维Hopf分岔边界Fig.3 Two-dimensional Hopf bifurcation boundary of P1-Q1

3.2 传输线路导纳对Hopf分岔的影响

图4为y0变化时的风电系统Hopf分岔曲线. 由图4可见, 线路的导纳参数对系统电压水平影响较小. 图5给出了系统导纳参数y0和ym共同作用下二维Hopf分岔边界. 由图4和图5可见, 随着线路导纳的增加, 系统分岔边界电压水平变化不大. 当y0=5.626 611时, 系统发生Hopf分岔, 如图4的H1, 当增大传输线路导纳y0时, 即缩短了线路的电气距离, 降低了线路所需的无功功率, 相应地, 系统供给风电场的无功功率也会增加, 因而使系统的Hopf分岔延后, 提高了系统电压的稳定性.

图4 y0变化时风电系统的Hopf分岔曲线Fig.4 Hopf bifurcation curve of wind power system with y0 variation

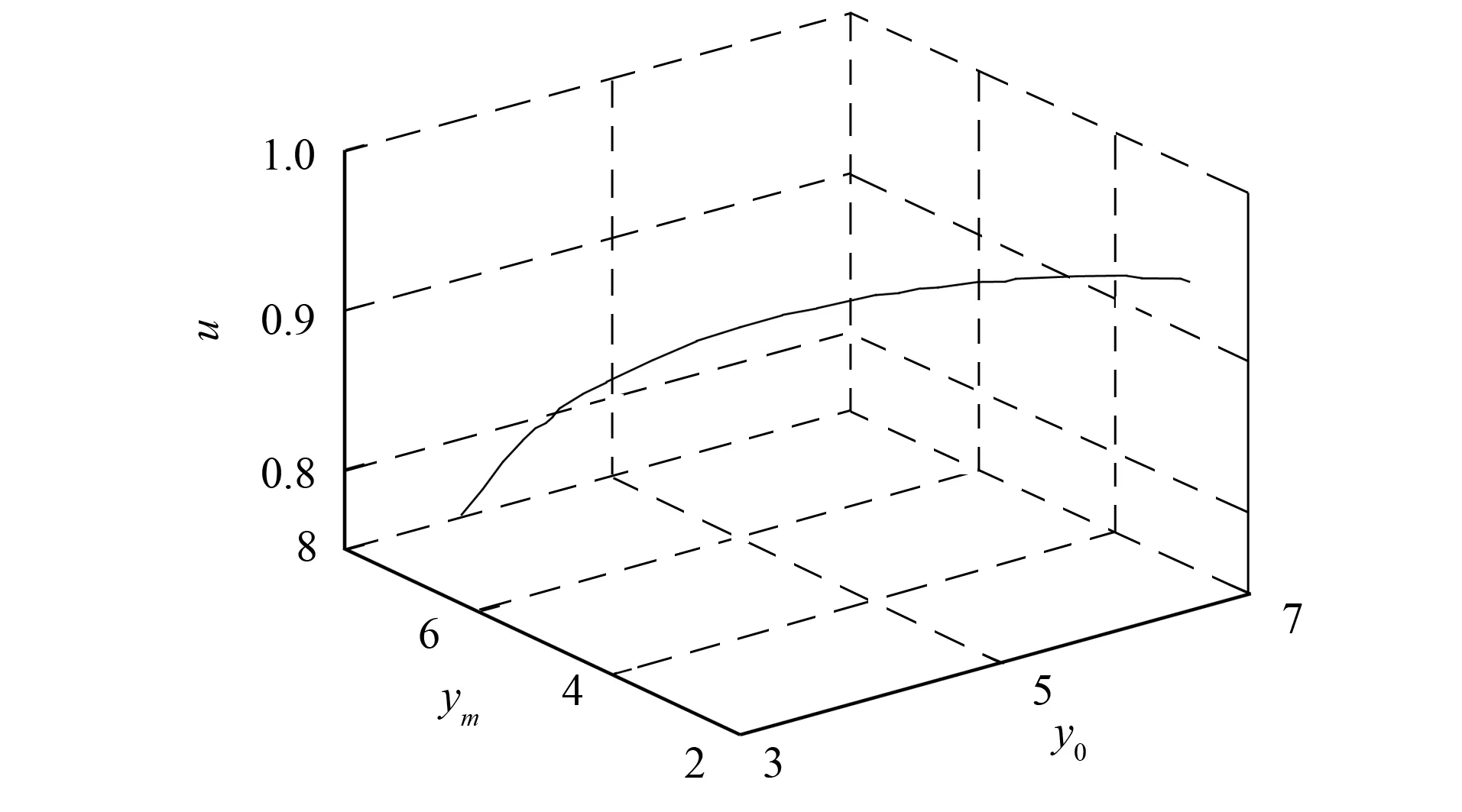
图5 y0-ym的二维Hopf分岔边界Fig.5 Two-dimensional Hopf bifurcation boundary of y0-ym

4 静止无功补偿器对Hopf分岔的影响

Hopf分岔可导致风电系统电压不稳定, 所以控制系统中的Hopf分岔能避免电压崩溃. 由上面分析可知, 系统Hopf分岔和无功功率关系密切, 而异步风电机组通常只能吸收无功, 无功控制主要依靠电容器就地补偿, 无法实现快速的无功调节. 静止无功补偿器(SVC)作为灵活的动态无功补偿装置, 在实际应用中可有效控制分岔[12].

本文采用在风电系统的风电场端安装静止无功补偿器有效控制无功功率, 如图6所示.

图6 加装SVC的风电系统模型Fig.6 Wind power system with SVC

数学模型为

(6)

其中：u表示补偿点电压；uref表示参考电压；Tr表示时间常数；Kr表示控制器增益；bSVC表示输出电压； 无功功率Q=bSVCu2.

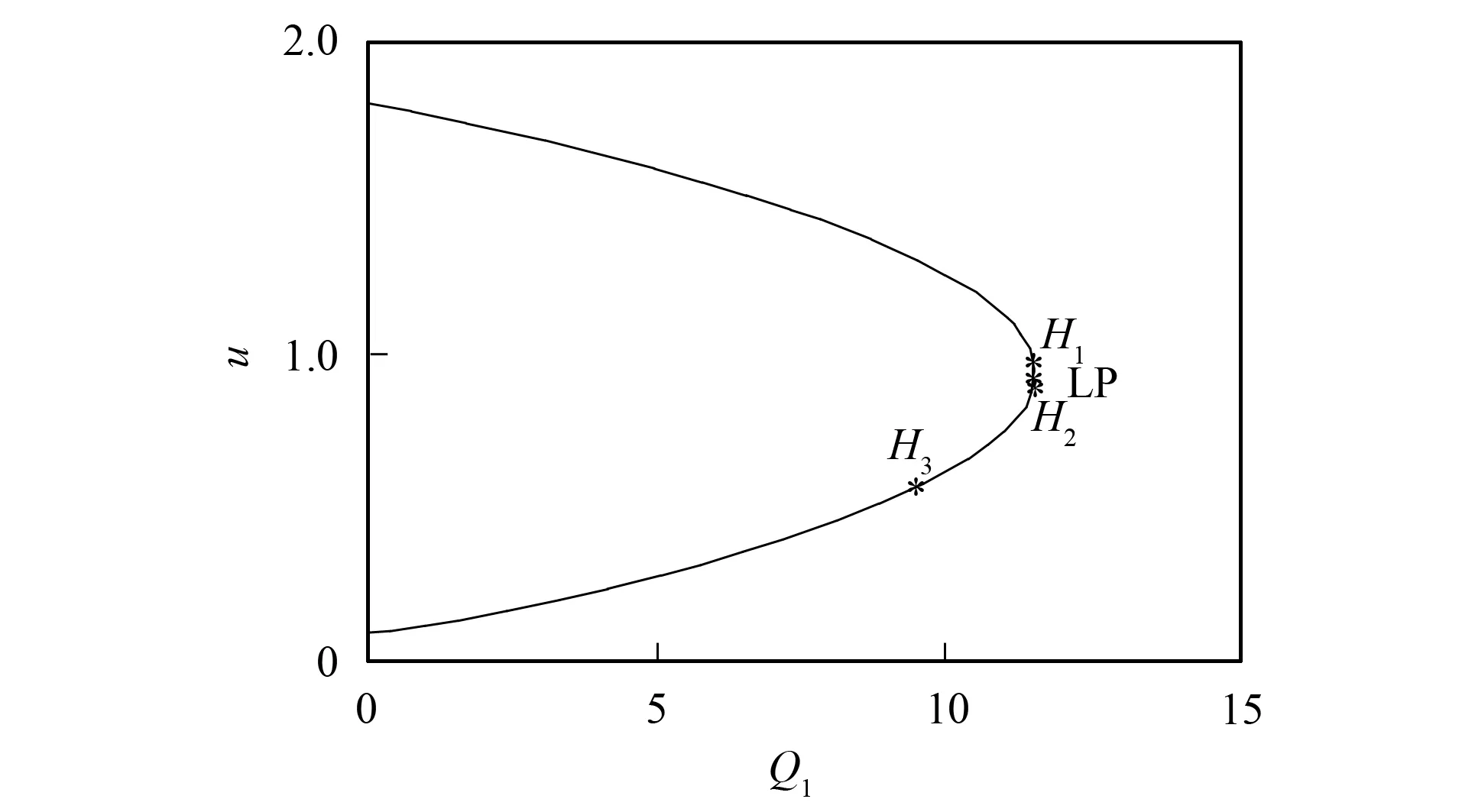
图7 加装SVC的风电系统Hopf分岔曲线Fig.7 Hopf bifurcation curve of wind power system with SVC

以Q1对风电系统的Hopf分岔影响为例, 分析静止无功补偿器对系统Hopf分岔及电压稳定性的影响. 当Kr=1.5,Tr=0.02时, 求得平衡点处风电场端电压数值随分岔参数Q1的变化情况如图7所示. 与图2比较可见, 含SVC的风电系统,Q1增加时, 提高了风电场的电压水平, 且系统的Hopf分岔点H1无限接近系统的LP点, 对应的无功功率也提高到Q1=11.531 989. 表明静止无功补偿器补偿了风电场吸收的无功功率, 同时延迟了Hopf分岔, 扩大了风电系统的电压稳定域.

综上所述, 本文应用延拓算法求取了风电系统的平衡解流形, 并针对几种分岔参数和静止无功补偿器对风电系统的Hopf分岔影响进行了研究, 进而分析了其对风电系统电压稳定性的影响： 1) 随着风电场发出有功功率的增加, 需减小风电场吸收的无功功率, 既避免了系统运行在Hopf分岔边界上, 又提高了系统电压水平; 2) 风电系统线路导纳的增加, 使风电系统的Hopf分岔延后, 增加了系统稳定域, 提高了风电系统的电压稳定性; 3) 静止无功补偿器为风电场有效提供了无功功率, 可延迟系统的Hopf分岔点, 增加负荷极限, 提高风电系统的电压稳定性.

[1] LIN Li, SUN Cai-xin, WANG Yong-ping, et al. Calculation Analysis and Control Strategy for Voltage Stability of Power Grid with Large Capacity Wind Farm Interconnected [J]. Power System Technology, 2008, 32(3)： 41-46. (林莉, 孙才新, 王永平, 等. 大容量风电场接入后电网电压稳定性的计算分析与控制策略 [J]. 电网技术, 2008, 32(3)： 41-46.)

[2] Vittal E, O’Malley M, Keane A. A Steady-State Voltage Stability Analysis of Power Systems with High Penetrations of Wind [J]. IEEE Transactions on Power Systems, 2010, 25(1)： 433-442.

[3] CHEN Ning, ZHU Ling-zhi, WANG Wei. Strategy for Reactive Power Control of Wind Farm for Improving Voltage Stability in Wind Power Integrated Region [J]. Proceedings of the CSEE, 2009, 29(10)： 102-108. (陈宁, 朱凌志, 王伟. 改善接入地区电压稳定性的风电场无功控制策略 [J]. 中国电机工程学报, 2009, 29(10)： 102-108.)

[4] ZHANG Feng, CHAO Qin. Research on Improving Transient Voltage Stability of Wind Farm by STATCOM [J]. Power System Technology, 2008, 32(9)： 70-73. (张锋, 晁勤. STATCOM改善风电场暂态电压稳定性的研究 [J]. 电网技术, 2008, 32(9)： 70-73.)

[5] WEI Xiao-guang, CHI Yong-ning, WEI Xiao-yun, et al. Transient Voltage Stability Enhancement of Induction Generator-Based Wind Farm by VSC-HVDC [J]. Transactions of China Electrotechnical Society, 2008, 23(5)： 100-107. (魏晓光, 迟永宁, 魏晓云, 等. 电压源换相高压直流输电改善异步发电机风电场暂态电压稳定性的研究 [J]. 电工技术学报, 2008, 23(5)： 100-107.)

[6] CHEN Yu-dong, PEI Chun-yan, CAO Zong-jie. Stability Analysis of Nonlinear System at Critical Point of Hopf Bifurcation [J]. Journal of Jilin University: Engineering and Technology Edition, 2009, 39(4): 993-996. (陈宇东, 裴春艳, 曹宗杰. 非线性系统Hopf分叉临界点的稳定性 [J]. 吉林大学学报: 工学版, 2009, 39(4): 993-996.)

[7] Radunskaya A, Williamson R, Yinger R. A Dynamic Analysis of the Stability of a Network of Induction Generators [J]. IEEE Transactions on Power Systems, 2008, 23(2)： 657-663.

[8] Kataoka Yoshihiko, Shinoda Yukio. Voltage Stability Limit of Electric Power Systems with Generator Reactive Power Constraints Considered [J]. IEEE Transactions on Power Systems, 2005, 20(2)： 951-962.

[9] LI Hong-zhong, CHENG Hao-zhong, TENG Le-tian, et al. A Direct Method for Computing Hopf Bifurcation Point in Power System Dynamic Voltage Stability [J]. Proceedings of the CSEE, 2006, 26(8)： 28-32. (李宏仲, 程浩忠, 滕乐天, 等. 以简化直接法求解电力系统动态电压稳定Hopf分岔点 [J]. 中国电机工程学报, 2006, 26(8)： 28-32.)

[10] JIANG Wei, WANG Cheng-shan, YU Yi-xin, et al. A New Method for Direct Calculation the Critical Point of Static Voltage Stability [J]. Proceedings of the CSEE, 2006, 26(10): 1-6. (江伟, 王成山, 余贻鑫, 等. 直接计算静态电压稳定临界点的新方法 [J]. 中国电机工程学报, 2006, 26(10): 1-6.)

[11] MA You-jie, ZHANG Ji-dong, ZHOU Xue-song, et al. Study on Steady State Voltage Stability of Power System Containing Wind Farm Based on Bifurcation Theory [J]. Power System Technology, 2008, 32(9)： 74-79. (马幼捷, 张继东, 周雪松, 等. 基于分岔理论的含风电场电力系统静态电压稳定问题研究 [J]. 电网技术, 2008, 32(9)： 74-79.)

[12] MA You-jie, WEN Hu-long, ZHOU Xue-song, et al. Calculation and Research of Two-Dimensional Parameter Bifurcation Boundary of Power System Voltage Stability Model with Wind Farm by Continuation Method [J]. Proceedings of the CSEE, 2011, 30(19)： 26-30. (马幼捷, 问虎龙, 周雪松, 等. 采用延拓法的风电系统稳定模型二维参数分岔边界的计算与研究 [J]. 中国电机工程学报, 2011, 30(19)： 26-30.)

[13] GUAN Qing-guang, ZANG Lin. Numerical Computation of Periodic Solutions Generated by Generalized Hopf Bifurcation of 3-Dimensional Piecewise Smooth Filippov-Type Equation [J]. Journal of Jilin University: Science Edition, 2010, 48(3): 371-374. (管庆光, 臧林. 三维分片光滑Filippov-型方程Hopf分支周期解的数值计算 [J]. 吉林大学学报: 理学版, 2010, 48(3): 371-374.)

[14] ZHANG Rui-ming, ZHANG Xin-yan. Study on Static Voltage Stability of Power System Based on Static Models of Common and Doubly Fed Asynchronous Generators [J]. Power System Technology, 2011, 35(1)： 175-179. (张瑞明, 张新燕. 基于普通异步发电机和双馈风力发电机静态数学模型的系统静态电压稳定性研究 [J]. 电网技术, 2011, 35(1)： 175-179.)