持续自适应的Web服务组合方法

付燕宁, 赵东范, 赵 健

(1. 吉林财经大学 信息经济学院, 长春 130122; 2. 吉林大学 计算机科学与技术学院, 长春 130012)

Web环境的改变可以导致过去是有效的组合服务不再有效, 过去是优化的组合服务不再优化, 组合服务性能可能会退化甚至无法运行. 文献[1]根据将具体服务绑定到组合规范的时机把基于过程的服务组合分为三类： 1) 在设计时确定具体的服务并将其绑定到组合规范； 2) 在组合服务执行前将过程模型中的任务绑定为服务, 然后引擎再执行组合服务； 3) 按照过程模型中任务间的执行逻辑, 逐步将过程模型中的任务绑定为服务并进行调用. 后两类在一定程度上适应了动态的Web环境, 但当用户再次发出同样的服务请求时, 则会出现以下问题： 第二类(如文献[2-3])将以往形成的服务组合当成最终版本, 每当用户再次发出服务请求时, 直接利用过去形成的组合服务, 不再探索新的服务组合, 这种处理方式只有对以往组合方案的利用, 而没有对环境的探索, 因此不能适应动态变化的Web环境； 第三类(如文献[4-5])将每次组合服务的执行都作为一个全新的问题, 重新探索新的环境形成新的组合服务, 这种处理方式只有对新环境的探索而缺乏对以往服务组合的利用, 导致增加系统开销. 这两类服务组合方式均缺乏对动态Web环境的可持续适应性, 因此, 将强化学习应用于基于过程的服务组合, 可使组合流程无论在何时运行, 均既可以利用以往获得的Web服务性能数据, 又能探索动态的Web环境, 在利用的基础上进行探索并调整组合策略, 持续适应不断变化的Web环境. 虽然文献[5-7]将学习机制用于动态Web环境下的Web服务组合, 但文献[5]仅考虑了组合服务每次执行时对环境的探索, 未考虑对以往形成的Web服务性能数据的再利用, 对Web服务及其性能的探索缺乏可连续性； 而文献[6-7]仅考虑了对以往数据的利用, 未考虑对环境的探索. 为解决对Web环境缺乏可持续适应性的问题, 本文根据解决该类服务组合的特点, 提出一种基于Markov决策模型的任务分配模型, 并为实现对动态变化的Web环境的可持续探索和利用, 提出了持续自适应服务组合方法.

1 任务分配模型

任务分配策略是将基于过程的任务分配视为随机顺序决策问题, 将任务分配过程分为若干个连续阶段, 利用强化学习技术在每个阶段尝试选择满足任务需求的Web服务, 并从选择的结果中进行学习, 在执行过程中逐步逼近从初始阶段到终止阶段累计代价最小的任务分配.

1.1 过程模型

服务请求的过程模型可形式化表示为SR=(T,R,δ), 其中:T={t1≤t≤m}表示一组构成服务请求的任务集合；R⊆T×T表示任务之间执行的次序; (t→t+1)∈R表示只有当t执行成功,t+1才开始执行；δ：T→D表示每个任务到抽象任务描述的映射,D表示抽象任务功能描述的集合, 即D={d1≤d≤m}.

抽象任务描述与任务一一对应, Web服务发现算法利用过程模型给出的抽象任务描述查找相应的服务.

1.2 候选服务集合

如果将发现服务的过程表述为函数φ：D→CS, 则任务t所对应的服务集合为CSt=φ(δ(t)), 该服务集合称为候选服务集合. 服务集合由功能相同、 QoS属性不同的一组服务组成.

如果将基于过程的任务分配分为若干阶段, 则这种组合问题具有如下特点： 每个任务分配对应一个阶段, 每个任务对应一个侯选服务集合, 即CS, 因此, 一个阶段即存在多种可能的任务分配, 需要在每个阶段确定出执行任务的Web服务； 在当前阶段确定了某个服务后, 则进入到下一阶段的某个状态(状态即一个阶段开始时算法所处的环境)并且Web服务的选择只取决于当前状态, 与过去各阶段的状态无关； 如果在每个阶段都根据某种标准确定出优化的Web服务, 则由各个阶段选择出的Web服务所构成的组合服务也是优化的. 因此, 这种服务组合问题实际上是随机顺序决策问题, Markov决策模型适合为该问题建模.

1.3 任务分配模型

基于Markov决策模型, 将任务分配问题表示为TAM=(k,s,ξ,ρ).

1)k表示任务分配阶段, 1≤k≤m. 若过程模型包含m个待分配的串型任务, 则基于过程的Web服务组合过程可被划分为m个连续阶段.

2)s表示在每个阶段开始时算法所处的状态. 初始阶段k=1, 只包括一个状态(即初始状态, 记为s0)； 其余各阶段k≠1, 所包含的状态数取决于前一阶段可供分配的Web服务数量； 特别当k=m时, 没有可用于分配的Web服务, 为了算法处理的需要, 需设定一个无代价的任务分配终止状态, 记为sd.

如果阶段k存在n个可供选择的Web服务, 表明阶段k的某个状态有n种可能的任务分配, 这种可能的任务分配完成后, 算法可能到达的状态称为可达状态. 如果阶段k的可达状态为n, 则阶段k+1存在n个状态.

尽管每个阶段可能有多种状态, 但在算法执行过程中只能处于某个阶段的某一种状态, 即在算法执行过程中, 状态和阶段是相对应的, 因此, 如果将某阶段k的某个状态记为s(k), 则s(k)也可以记为s； 同理,CS(k)也可记为CS(s).

3)ξ:πs(w)→w是Web服务选择函数, 表示在状态s(k)根据概率分布πs(w)为该状态所对应的任务选择Web服务.πs(w)是在状态s上关于Web服务的概率分布(简称为状态s的概率分布). 如果状态s的候选服务集为CS(s)={w1,w2,w3}, 则其概率分布πs(w)是πs(w1),πs(w2),πs(w3). 概率分布实质是关于代价rk(w)的多项式函数,rk(w)是关于Web服务某种性能的实际观察值函数.

4)ρ: (s(k),ξ)→s(k+1)是状态转移函数, 表示在当前状态s(k), 由函数ξ(πs(w))做出了某种任务分配, 下一个阶段的某个状态s(k+1)也就完全确定了, 即表示在状态s(k)完成任务分配后转换到下一个状态s(k+1).

因此, 任务分配模型具有如下特点： 一旦在某个状态选定了一个服务, 则下一个阶段的某个状态也就确定了, 即s′=ρ(s,w); 并且不同的服务选择可导致不同的状态, 即ρ(s,w1)≠ρ(s,w2).

1.4 策略Π

策略Π由各阶段(或状态)上的服务选择函数ξ组成, 即Π={ξkk=1,2,…,m}. 由于ξ由各阶段上的概率分布决定, 因此, 策略Π也可定义为是由各阶段上的概率分布组成的, 即Π={πs(w)s=1,2,…,m}.m个阶段的任务分配过程包括m个状态转换, 与任务分配模型相对应的任务分配状态转移如图1所示, 表示了各阶段的状态及状态转移.

图1 任务分配状态转移Fig.1 Task allocation transition

假设服务请求模型包括4个任务, 存在13个可供分配的Web服务, 其中,CS(1),CS(2),CS(3),CS(4)分别为4,4,3,2, 阶段1～阶段5的状态数分别为1,4,4,3,2. 图1中节点表示任务分配状态, 边表示状态转移； 实线边表示实际转移, 虚线边表示可能的状态转移； 实心节点表示实际到达的状态, 空心节点表示可能达到的状态.

算法从初始状态出发直到终止状态通过学习机制逐步逼近一条累计代价的优化路径. 在初始状态, 有4个可供分配的Web服务, 算法根据函数ξ为任务1选择某个Web服务后, 到达下一个状态2(图1中实心节点所示)； 通过服务的执行获得其实际执行代价, 计算该状态的概率分布πs(w), 对于其他状态算法重复上述过程, 直至终止状态. 通过学习算法不断地执行, 不断更新服务组合策略, 逐步逼近从初始状态到终止状态的优化任务分配策略.

2 主要方法

2.1 选择Web服务的依据

当将QoS作为选择服务的依据时, 要注意服务提供者所给出的性能发布值是否能准确反映Web服务的实际性能, 否则会将不是真实性能的Web服务加入到组合中而影响组合服务的性能, 因此在选择Web服务时要根据Web服务执行的实际性能, 而不是根据服务提供者所发布的性能. 文献[8-10]使用“信任”从一组执行同样任务的服务中选择优化的Web服务, 利用Web服务使用者给出的评价计算信誉. 这种计算信誉度的弊端是采用了使用者的主观评价, 而不同使用者的评价标准不同, 因此, 人为的评价不一定能反映Web服务的真实性能. 本文选择某种QoS性能参数的信誉度作为选择Web服务的依据, 通过比较所观察到的Web服务实际性能和Web服务提供者所发布的性能计算信誉度.

对于服务, 其参数k的信誉度函数为

(1)

2.2 选择Web服务的技术

根据任务分配模型可知, 该结构恰好对应确定性最短路径, 可考虑采用动态规划或强化学习解决这种优化问题. 由于将Web服务的实际性能参数作为选择Web服务的依据, 因此, 在Web服务执行前, 算法并不能获得Web服务的实际性能, 这样每个状态的概率分布事先并不可知. 如果在概率分布未知的情况下, 优化问题则转化为强化学习问题, 通过值迭代或策略迭代的方式逼近MDP中的最优策略. 根据Bellman最优定理, 对于状态空间有限的单链MPD问题, 必然存在一个最优策略[11]； 同理, 对于服务选择问题也必然存在一个最优的任务分配策略Π={πs(w)s=1,2,…,m}.

因此, 采用如下在线概率分布模型[12]:

(2)

(3)

综上可知, 概率分布取决于服务执行的实际代价, 同时也受θs(即熵)的制约, 可通过事先指定各状态的熵值, 确定各状态的探索级别.

2.3 控制随机选择

探索是尝试解决新问题的方法, 而利用是重用曾经成熟的解决方案. 因此, 既要使算法保持一定程度上的探索, 还要使其利用以往获得的Web服务性能数据. 探索和利用间的平衡问题是学习算法要解决的问题之一, 强化学习是以集成方式确切地处理探索和利用之间的平衡问题及概率分布的在线估计问题[12], 为了量化探索, 利用候选服务集概率分布的熵定义各状态的探索度.

3 算法与分析

3.1 学习算法

该算法的主要步骤是从初始状态s0出发, 在每个状态s根据概率分布πs(w)选择一个服务w并执行该服务, 根据服务执行产生的实际代价, 更新c(s,w),πs(w)和U(s), 然后转移到新的状态s′. 重复这个过程直至终止状态. 由于sd是终止状态, 因此sd的代价为0. 其中,c(s,w),πs(w),U(s)需要预先给定初始值, 一般情况下, 令πs(w),U(s)的初始值为1/ns和0, 当πs(w)=1/ns时,c(s,w)的初始值已经不再重要. 算法步骤如下:

WSCompositionPolicy(entropyπ)

1) begin

2)t← identifyTask(SR)

3)CSt=φ(δ(t))

4) if (s≠sd)

5)w←ξ(πs(w))

6) execution(w)

7)c(s,w)=rk(w)

8)θs← computeTeta(πs(w))

10) goto 2)

11) endif

12) end

该算法在不同状态与不同的环境交互, 通过步骤3)感知Web环境中服务的变化. 在步骤5)和步骤6)尝试选择执行任务的Web服务, 如何尝试取决于该状态的概率分布. 步骤7)表明算法根据Web服务的执行而观察到该服务实际执行性能(在动态环境下随时间的改变而改变), 并由此计算出rk(w). 步骤9)更新该状态的概率分布, 之后学习算法进入下一个任务分配状态s+1, 直至终止状态sd. 注意算法第一次执行时, 根据初始概率分布选择执行任务的Web服务.

该算法每次执行都是自学习、 自适应过程, 通过算法的不断执行, 算法不断地获得所选中Web服务的执行代价, 根据该代价不断更新各状态的概率分布, 逐渐逼近一个优化的任务分配策略, 即Π={πs(w)s=1,2,…,m}.

3.2 算法分析

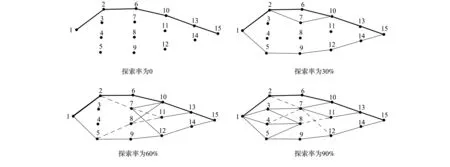
当θs=0时, 概率分布退化为πs(w)=1/ns, 熵值Es=logns, 所有状态的探索度达到最大值, 此时算法总是处于随机探索状态, 不计代价随机地选取一个Web服务进行任务分配, 不再利用以往学习到的策略. 因此, 当0

通过上述分析可知, 合理地给定熵值Es, 该算法即可逐步逼近一个优化的服务选择策略. 每当Web环境发生变化时, 该算法都能动态地调整服务组合策略； 如果Web环境未发生变化, 则可利用由Web服务以往性能参数所学习到的组合策略.

4 实验结果与分析

为了验证算法对环境变化的适应性, 本文通过给定不同的探索率, 考察算法在静态和动态两种环境下对环境的探索程度. 每次模拟实验开始, 令U(s)和πs(w)的初始值为0和1/ns, 且每个状态的探索率都相同；根据方程(3)和(4)在每一步更新平均代价和转换概率.

4.1 静态环境

当探索率分别为0,30%,60%和90%时, 通过算法探索的路径, 考察算法对探索率的变化规律. 路径[1,2,6,10,13]上边的代价初始值为1, [1,5,9,12,14]上边的代价为2, 而其他边的代价初始值为3, 由于15是终止状态, 因此[13,15], [14,15]的代价始终为0. 图2给出了算法运行10 000次(一次运行表示一次完整的任务分配)探索的路径. 图2中粗线边表示高访问率, 细线边表示较高访问率, 长虚线表示中访问率, 短虚线表示低访问率.

图2 算法在4种不同探索率下的探索路径Fig.2 Paths from source to destination for four exploration rates

当探索率为0时, 一旦找到从节点1到节点15的最短路径, 即[1,2,6,10,13,15](图2粗线边所示路径), 则算法不再进行探索, [1,2,6,10,13,15]是唯一的遍历路径； 当探索率为30%时, 尽管探索到了其他边, 但最短路径仍然是[1,2,6,10,13,15], 表明对原有组合的利用大于探索； 当探索率为60%时, 算法探索了更多的边, 但仍然采用[1,2,6,10,13,15]作为最短路径, 虽然增加了探索, 但探索仍然低于利用； 当探索率为90%时, 不再利用原来的最短路径, 探索明显大于利用. 因此, 随着探索率的提高, 算法的探索程度逐渐加大.

4.2 动态环境

当探索率分别为0,30%,60%和90%时, 通过执行代价变化趋势, 考察算法在不同探索率下对环境变化的适应性. 图3给出了随着算法运行次数的增加, 算法执行代价的变化规律.

图3 4种探索率的算法执行代价Fig.3 Cost trends for four exploration rates

初始时, 路径[1,2,6,10,13]上边的代价为3, [1,5,9,12,14,]上边的代价为4, 其他边的代价为6, 边[13,15],[14,15]的代价仍然为0. 此时最短路径为[1,2,6,10,13,15], 该路径的总代价是12. 对不同探索率算法分别执行13 000次, 当算法执行到7 501次时, 将所有内部边的代价置为1, 此时观察算法对不同探索率的变化规律. 由图3可见, 虽然内部边的代价发生了变化, 在整个模拟实验过程中算法执行代价始终为12, 原因是在探索率为0时, 尽管某些边代价发生了改变, 产生了新的最短路径, 但算法不再进行探索； 当探索率不为0时, 算法可以在环境发生变化的情况下找到新的优化路径(所有经过内部节点3,4,7,8,11经过13到达15的路径是最短路径), 代价由12变为4且探索率越高, 找到新优化路径的速度越快, 其原因是当探索率不为0时, 算法可对环境进行探索发现性能更好的Web服务, 对原来形成的组合策略进行调整.

[1] Stephan Leutenmayr. Selected Languages for Web Services Composition: Survey, Challenges, Outlook [D]: [Ph D Thesis]. Munich: University of Munich, 2007.

[2] CHEN Yan-ping, LI Zeng-zhi, TANG Ya-zhe, et al. A Method Satisfying Markov Process of Web Service Composition under Incomplete Constrains [J]. Chinese Journal of Computers, 2006, 29(7): 1076-1083. (陈彦萍, 李增智, 唐亚哲, 等. 一种满足马尔可夫性质的不完全信息下的Web服务组合方法 [J]. 计算机学报, 2006, 29(7): 1076-1083.)

[3] LIU Shu-lei, LIU Yun-xiang, ZHANG Fan, et al. A Dynamic Web Services Selection Algorithm with QoS Global Optimal in Web Services Composition [J]. Journal of Software, 2007, 18(3): 646-656. (刘书雷, 刘云翔, 张帆, 等. 一种服务聚合中QoS全局最优服务动态选择算法 [J]. 软件学报, 2007, 18(3): 646-656.)

[4] ZENG Liang-zhao, Benatallah B, Dumas M, et al. Quality Driven Web Service Composition [C]//Proceedings of the 12th International Conference on World Wide Web. New York: ACM, 2003: 411-421.

[5] FAN Xiao-qin, JIANG Chang-jun, WANG Jun-li, et al. Random-QoS-Aware Reliable Web Service Composition [J]. Journal of Software, 2009, 20(3): 546-556. (范小芹, 蒋昌俊, 王俊丽, 等. 随机QoS感知的可靠Web服务组合 [J]. 软件学报, 2009, 20(3): 546-556.)

[6] Abdallah S, Lesser V. Modeling Task Allocation Using a Decision Theoretic Model [C]//Proceedings of the Fourth International Joint Conference on Autonomous Agents and Multiagent System. New York: ACM, 2005: 719-726.

[7] Hannah H, Mouaddib A I. Task Selection Problem under Uncertainty as Decision-Making [C]//Proceedings of the First International Joint Conference on Autonomous Agents and Multiagent System. New York: ACM, 2002: 1303-1308.

[8] Maximilien E M, Singh M P. Multiagent System for Dynamic Web Services Selection [C]//Proceedings of 1st Workshop on Service-Oriented Computing and Agent-Based Engineering. Netherlands: [s.n.], 2005: 25-29.

[9] ZHAI Hong-yi. Management Tool Design for IP QoS Policy [J]. Journal of Jilin University: Information Science Edition, 2011, 29(3): 225-230. (翟红艺. IP网络QoS策略管理工具设计 [J]. 吉林大学学报: 信息科学版, 2011, 29(3): 225-230.)

[10] ZHU Mei-ling, ZHAO Xiao-hui, GU Hai-jun, et al. Adaptive Resource Allocation Algorithm for Multiuser OFDM System Based on QoS [J]. Journal of Jilin University: Engineering and Technology Edition, 2009, 39(5): 1347-1352. (朱美玲, 赵晓晖, 顾海军, 等. 基于QoS的多用户OFDM系统自适应资源分配算法 [J]. 吉林大学学报: 工学版, 2009, 39(5): 1347-1352.)

[11] GAO Yang, ZHOU Ru-yi, WANG Hao, et al. Study on an Average Reward Reinforcement Learning Algorithm [J]. Chinese Journal of Computers, 2007, 30(8): 1372-1378. (高阳, 周如益, 王皓, 等. 平均奖赏强化学习算法研究 [J]. 计算机学报, 2007, 30(8): 1372-1378.)

[12] Achbany Y, Fouss F, Yen L, et al. Optimal Tuning of Continual Online Exploration in Reinforcement Learning [C]//Proceedings of the International Conferrence on Artificial Neural Networks. Berlin: Springer, 2007: 790-800.