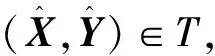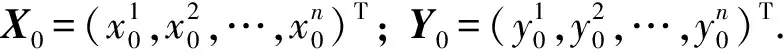矩阵型网络DEA模型解的存在性及其性质

程 昀, 杨印生, 盛学之

(1. 吉林大学 管理学院, 长春 130025； 2. 山东大学威海分校 机电与信息工程学院, 山东 威海 264209；3. 密歇根州立大学 数学系, 美国 东兰辛 48823)

网络DEA[1]主要针对复杂系统相对有效性(简称效率)的求解问题. 常见的复杂系统有链式结构、 环型结构和复合结构, 分别如图1～图3所示. 这些复杂结构的系统统称为网络结构, 求解其效率的DEA方法统称为网络DEA方法. 文献[2-6]以供应链系统结构为主, 构建了串型系统DEA效率评价模型； 文献[7-10]针对并型独立子系统提出了一系列DEA效率评价模型; 文献[11]基于静态情形, 得到了以效率区间表示的环型系统效率. 但对于如图3所示的不同阶段、 不同层次的子系统都存在投入产出关系, 每个子系统还存在外部投入产出关系, 系统之间构成很多环型结构的这类复合系统, 目前对其提出具体的网络DEA模型报道较少.

图3所示的系统内部纵横交错, 类似多维矩阵的形式, 该类系统称为矩阵型网络系统. 基于生命周期评价(LCA)的供应链管理系统、 投入产出系统等均为此类结构形式. 对于3个子系统的矩阵型网络结构, Amatatsu等[12]在SBM模型[13-14]的基础上, 提出一个网络DEA模型, 但未对该模型解的存在性及性质进行讨论. 本文针对图3所示的n个子系统的矩阵型网络结构进行分析, 提出了求解其效率的网络DEA模型, 证明了新模型解的存在性, 给出了决策单元弱DEA有效性的定义, 并讨论了决策单元的弱DEA有效性与相应多目标规划弱Parteo解的关系.

图1 链式结构的串型结构(A)和并型结构(B)Fig.1 Serial stucture (A) and parallel stucture (B) of chain stucture

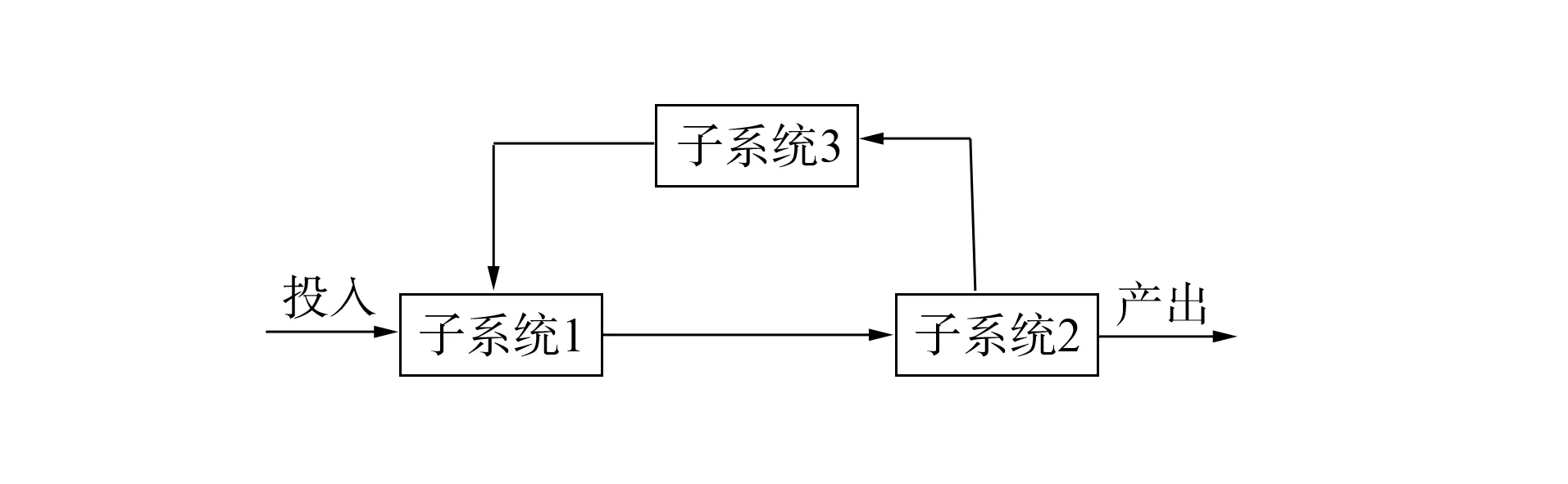
图2 环型结构Fig.2 Ring structure

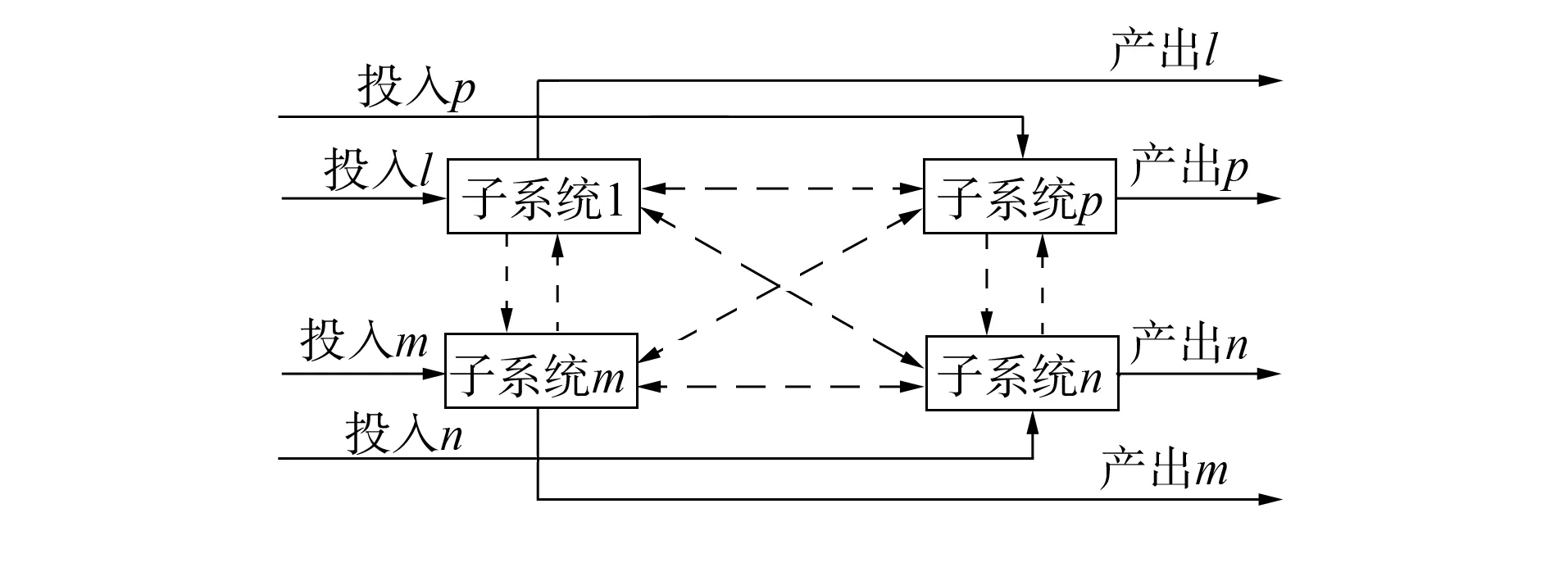
图3 复合结构Fig.3 Composite structure

1 矩阵型网络系统DEA模型及其对偶

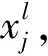
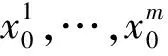
(1)

易得矩阵型网络DEA模型(1)的对偶模型如下：

(2)

显然, 矩阵型网络DEA模型及其对偶模型均为线性规划模型.

2 矩阵型网络DEA模型解的存在性

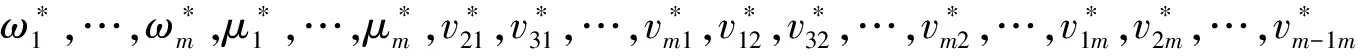
(3)

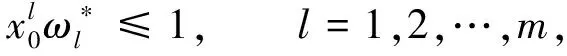
(4)

将不等式(3)中的l=1,2,…,m累加, 得

整理可得

(5)

由对偶理论可知, 模型(1)与对偶模型(2)的最优值相同, 即

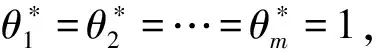
3 矩阵型网络DEA模型解的性质

考虑如下多目标规划：

(6)

其中

为矩阵型网络DEA模型(1)的生产可能集.

定义2设(X*,Y*)∈T, 若不存在(X,Y)∈T, 使得F(X,Y)

引理1设(X0,Y0)为多目标规划(6)对应的线性加权问题

的最优解, 若(ω0T,μ0T)≥0, 则(X0,Y0)为多目标规划(6)的弱Pareto解.

定理2若决策单元DMUj 0是弱DEA有效的, 则(X0,Y0)必为多目标规划(6)的弱Pareto解.

且k≠l,

(11)

则由式(8)可知

(12)

进一步整理不等式(12)左边后两项可得

再结合不等式(11)可得

(13)

则

(14)

因此, 对∀(X,Y)∈T, 结合式(14)有

即(X0,Y0)为多目标问题(6)相应于以ω*,μ*≥0为权的如下线性加权和问题的最优解:

从而由引理1知, (X0,Y0)为多目标问题(6)的弱Pareto解.

综上, 本文通过建立矩阵型网络DEA模型解决了矩阵型网络结构的效率评价问题. 新模型的性质表明, 新模型在矩阵型网络结构的效率评价方面可行、 有效.

[1] Fare R, Grosskopf S. Network DEA [J]. Socio-Economic Planning Sciences, 2000, 34(1): 35-49.

[2] Sexton T R, Lewis H F. Two-Stage DEA: An Application to Major League Baseball [J]. Journal of Productivity Analysis, 2003, 19(2/3): 227-249.

[3] CHEN Yao, LIANG Liang, YANG Feng, et al. Evaluation of Information Technology Investment: A Data Envelopment Analysis Approach [J]. Computers & Operations Research, 2006, 33(5): 1368-1379.

[4] BI Gong-bing, LIANG Liang, YANG Feng. A DEA-Based Efficiency-Measuring Model for a Two Stage Production System [J]. Chinese Journal of Management Science, 2007, 15(2): 92-96. (毕功兵, 梁樑, 杨锋. 两阶段生产系统的DEA效率评价模型 [J]. 中国管理科学, 2007, 15(2): 92-96.)

[5] WEI Quan-ling, PANG Li-yong. The Chain Network with Stages’Final Output DEA Models [J]. Mathematics in Practice and Theory, 2010, 40(10): 53-60. (魏权龄, 庞立永. 具有阶段最终产出的链式网络DEA模型 [J]. 数学的实践与认识, 2010, 40(10): 53-60.)

[6] KAO Chiang, HWANG Shiuh-nan. Efficiency Decomposition in Two-Stage Data Envelopment Analysis: An Application to Non-life Insurance Companies in Taiwan [J]. European Journal of Operational Research, 2008, 185(1): 418-429.

[7] YANG Ying-sheng, MA Ben-jiang, Koike M. Efficiency-Measuring DEA Model for Production System withkIndependent Subsystems [J]. Journal of the Operations Research Society of Japan, 2000, 43(3): 343-354.

[8] DUAN Yong-rui, TIAN Peng, ZHANG Wei-ping. DEA Models with Independent Subsystems and Their Application [J]. Journal of Industrial Engineering/Engineering Management, 2006, 20(1): 27-31. (段永瑞, 田澎, 张卫平. 具有独立子系统的DEA模型及其应用 [J]. 管理工程学报, 2006, 20(1)： 27-31.)

[9] KAO Chiang. Efficiency Measurement for Parallel Production Sysytems [J]. European Journal of Operational Research, 2009, 196(3): 1107-1112.

[10] YANG Feng, LIANG Liang, LING Liu-yi, et al. DEA Efficiency Evaluationg Models for DMUs with Parallel Structure [J]. Chinese Journal of Management Science, 2009, 17(6): 157-162. (杨锋, 梁樑, 凌六一, 等. 并联结构决策单元的DEA效率评价研究 [J]. 中国管理科学, 2009, 17(6): 157-162.)

[11] YANG Feng. Efficiency Evaluation of DMUS with Multiple Subsystems [D]: [Ph D Thesis]. Hefei: University of Science and Technology of China, 2006. (杨锋. 含有多个子系统的决策单元的DEA效率评估研究 [D]: [博士学位论文]. 合肥： 中国科技大学, 2006.)

[12] Amatatsu H, Ueda T. Input-Output Tables and Network DEA: Efficiencies of the 47 Prefectures of Japan [C]//DEA Symposium 2009. Osaka: Osaka University, 2009: 91-97.

[13] Tone K. A Slacks-Based Measure of Super-Efficiency in Data Envelopment Analysis [J]. European Journal of Operational Research, 2002, 143(1): 32-41.

[14] Tone K, Tsutsui M. Network DEA: A Slacks-Based Measure Approach [J]. European Journal of Operational Research, 2009, 197(1): 243-252.