基于改进自适应模糊推理系统的YG3硬质合金精密外圆磨削表面质量预测

刘茂福

湖南机电职业技术学院，长沙，410151

0 引言

近年来，硬质合金材料以其硬度高、断裂韧性和抗弯强度大以及优良的耐腐蚀性和耐高温性等特点，广泛应用于航空航天、国防、机械、汽车等行业的切削工具、模具、结构零件、耐磨零件等的制造中［1］，典型零件如各种硬质合金轴、销等回转类零件。目前，硬质合金材料零部件的坯料是由难熔的金属碳化物（如 WC）及金属粘结剂（如Co）经粉末冶金方法烧结制备而成的。而其后续半精加工及精加工则主要采用树脂基金刚石砂轮进行精密磨削以保证表面质量和尺寸精度［2］。因此，为了提高硬质合金材料零部件的表面完整性和表面质量，获得所要求的几何精度，提高加工效率并降低加工成本，有必要对其精密磨削后表面质量的预测技术进行研究。

由于精密磨削加工是一个复杂的非线性过程，影响零部件表面质量的因素众多，一般采用表面粗糙度来表征其表面质量。传统的预测方法主要是通过试验数据的多元回归分析来预测磨削加工后的表面粗糙度［3］，但这一方法由于难以找到适当的回归模型而导致预测精度不高。文献［4］中采用BP神经网络对磨削表面粗糙度进行了预测，但该方法存在全局搜索能力弱、收敛速度慢、易陷入局部极小值等缺点。而自适应模糊推理系统（adaptive network－based fuzzy inference system，ANFIS）融合了神经网络的学习机制和模糊系统的语言推理能力等优点，克服了上述神经网络的缺点和模糊系统的偶然性，已在非线性系统建模、故障诊断、噪声处理等领域得到应用［5－7］。本文以YG3硬质合金精密外圆磨削表面的表面粗糙度为研究对象，建立了基于ANFIS的预测模型。同时为了确定合适的隶属函数及搜索最佳参数，进一步提高所建立的ANFIS预测模型的精度，引入混合田口遗传算法（hybrid Taguchi genetic algorithm，HTGA）对预测模型进行了改进。最后，进行了YG3硬质合金精密外圆磨削工艺试验，采用相应的磨削加工参数及测得的表面粗糙度作为训练样本和测试样本，通过对BP神经网络模型、传统ANFIS预测模型及改进ANFIS预测模型这三种模型的预测结果进行对比分析，验证了所提出的改进ANFIS表面粗糙度预测模型的有效性。

1 基于ANFIS的表面粗糙度预测模型的建立

1.1 精密外圆磨削的一般过程

典型精密外圆磨削通常分为纵向磨削法和横向磨削法，本文采用的是纵向磨削法。其中，砂轮以线速度vs旋转，工件以线速度vw旋转，两者在接触处旋转方向相反，同时工件与磨床工作台一起以进给速度vf做纵向往复运动。每一纵向行程或往复运动终了时，砂轮按给定的磨削深度ap做一次横向进给。

1.2 基于ANFIS的表面粗糙度预测模型的建立

参照典型ANFIS结构［5-7］，本文采用如图1所示的ANFIS结构，选取对YG3硬质合金精密外圆磨削表面粗糙度影响较大的四个参数——砂轮线速度vs、工件线速度vw、进给速度vf、磨削深度ap作为ANFIS的输入变量，而磨削后工件表面粗糙度Ra作为ANFIS的输出变量，则具有n个模糊if－then规则的规则集可表示为

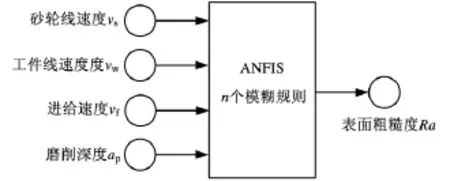
图1 基于ANFIS的表面粗糙度预测模型

这里，Rl（l＝1，2，… ，n）表示规则集中第l个规则，Ah、Bi、Cj及Dk（h，i，j，k＝1，2，3，4）分别为具有隶属函数μAh（vs）、μBi（vw）、μCj（vf）及μDk（ap）的前件部分的语言变量，fl为输出变量，而pl、ql、rl、sl和tl是后件参数。从式（1）中推导出的ANFIS输出可以表示为

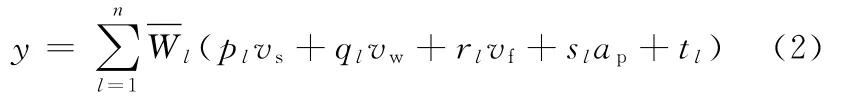
即预测的表面粗糙度，且有

式中，α为用于试验数据训练的组数；Ram为试验测得的表面粗糙度；Ra′m为预测得到的表面粗糙度。

由式（4）可知，性能指标J的值实际上依赖于集合 ｛aAh，bAh，aBi，bBi，aCj，bCj，aDk，bDk，pl，ql，rl，sl，tl｝，则有

上述问题等价于以下优化问题：

式（6）是一个具有连续变量的非线性函数。下面采用混合田口遗传算法搜索式（6）所示优化问题的最优解。

2 基于HTGA的ANFIS预测模型的改进

为确定合适的隶属函数及搜索最佳的参数，并进一步提高所建立的ANFIS预测模型的精度，引入了HTGA对ANFIS预测模型进行改进。本文采用的HTGA方法［8－9］结合了传统遗传算法（traditional genetic algorithm，TGA）和田口方法（Taguchi method），并将正交试验设计的思想引入到遗传算法中。田口方法在TGA的交叉和变异操作之间引入，通过采用田口方法的两个主要工具——信噪比（signal－to－noise ratio）和正交矩阵（orthogonal array）将田口方法的系统推理能力并入交叉操作中，以系统地选择更优的基因实现交叉操作。该方法不仅可以找到最优解或次优解，而且具有更好的收敛性，增强了遗传算法的处理能力，避免了传统遗传算法存在的近亲繁殖、早熟收敛等缺陷。图2为基于HTGA的优化过程的流程图。

图2 基于HTGA的优化过程流程图

3 预测结果及分析

3.1 YG3硬质合金精密外圆磨削试验

YG3硬质合金精密外圆磨削试验在一台MB1320／H半自动精密外圆磨床上进行，整个磨削试验系统如图3所示。砂轮架的横向进给和工作台的往复运动分别由两台步进电机控制，通过工控机发出步进脉冲给步进电机驱动器，由驱动器驱动步进电机实现启停和调速控制，完成纵向和横向的进给运动。通过控制两台变频器，可对砂轮电机和工件电机进行变频调速，实现对砂轮和工件转速的变速及控制。通过尺寸传感器监测工件的径向尺寸，通过光栅尺测量工作台的位移和砂轮架位移。所有信号都经由转换卡进行数据采集，并输入工控机中进行集中控制与处理。

砂轮采用树脂结合剂金刚石砂轮，砂轮规格如表1所示，在试验之前须对砂轮进行精密整形与修锐，以保证砂轮的正确形状和锋锐性，磨削液采用普通水基磨削液。工件采用经粗磨后直径为15mm、长度为80mm的YG3硬质合金棒料，材料性能如表2所示。试验当中采用的具体磨削参数如表3所示。磨削后工件表面粗糙度Ra采用Hommel T1000粗糙度仪离线测量。

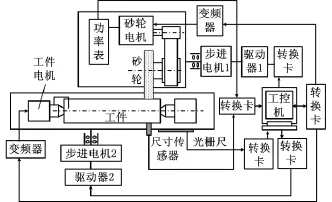
图3 YG3硬质合金精密外圆磨削试验系统

表1 砂轮规格

表2 实验用YG3硬质合金材料特性

表3 磨削参数

3.2 样本选择及参数设置

由于影响表面粗糙度的主要因素是磨削参数，因此本文选取砂轮线速度vs、工件线速度vw、进给速度vf、磨削深度ap作为所建立的改进ANFIS预测模型的输入变量，而磨削后工件表面粗糙度Ra为该模型的输出变量。用于预测模型训练和测试的样本来自于以上YG3硬质合金精密外圆磨削工艺试验，其中的36组数据作为所建立的预测模型的训练样本，而另外18组数据作为测试样本。

根据所提出的预测模型，在 MATLAB 7.0中编制相应的程序，同时对预测模型各参数设置如下：模型所采用的模糊规则数n＝20，根据式（4）、式（5）得到前后件参数的总数为132（即β＝132），种群数量 M＝300，交叉概率Pc＝0.9，变异概率Pm＝0.1，进化代数为300，隶属函数采用高斯隶属函数，正交矩阵采用L256（2255）。

3.3 预测结果分析

用相对误差Er和均方根相对误差EMSRE作为最终评价指标：

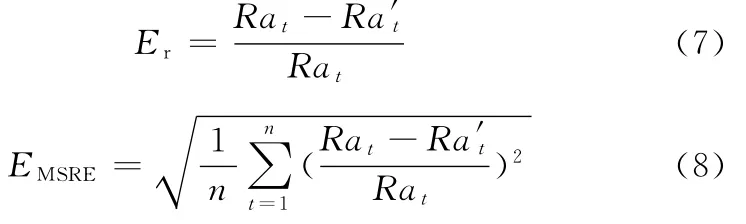
式中，Rat、Ra′t分别为试验和预测获得的表面粗糙度值；n为数据的组数。

表4所示为表面粗糙度试验结果与不同模型预测结果的对比，表中Ra0为试验测得的工件表面粗糙度值，Ra1、Ra2、Ra3分别为采用BP神经网络模型、传统ANFIS预测模型及改进ANFIS预测模型预测获得的表面粗糙度值，而Er1、Er2、Er3分别为采用上述三种预测模型时试验值与预测值之间的相对误差，三种预测模型的预测误差分析比较结果如图4所示。从表4和图4中可以看出，采用改进ANFIS预测模型时，在18组数据中有10组相对误差的绝对值小于4%，其中最小的为2.06%；采用BP神经网络模型时，相对误差绝对值最大为13.07%，最小值为5.29%，在18组数据中有14组相对误差的绝对值在6%～10%之间；采用传统ANFIS预测模型时，相对误差绝对值最大为7.51%，最小值为4.20%，在18组数据中有16组相对误差的绝对值在4%～7%之间。由三者的均方根相对误差可知，采用改进ANFIS预测模型时的均方根相对误差仅为4.13%，与BP神经网络模型和传统ANFIS预测模型相比，分别低4.57%和1.48%。从预测值相对误差的分布及均方根相对误差的大小来看，本文提出的改进ANFIS预测模型的预测精度均高于BP神经网络模型和传统ANFIS预测模型。

表4 表面粗糙度实验结果与不同模型预测结果对比

图4 三种预测模型的预测误差分析比较

4 结语

本文建立了基于ANFIS的YG3硬质合金精密外圆磨削表面粗糙度的预测模型，并引入了HTGA方法对所提出的预测模型进行了改进。完成了YG3硬质合金精密外圆磨削工艺试验，从试验数据中分别选取训练样本和测试样本，对所提出的改进ANFIS表面粗糙度预测模型的有效性和预测精度进行了验证。经过对BP神经网络模型、传统ANFIS预测模型及改进ANFIS预测模型三者预测结果的对比分析可知，从预测值相对误差的分布及均方根相对误差的大小来看，本文所提出的改进ANFIS表面粗糙度预测模型均具有较高的预测精度，该模型是一种有效的硬质合金精密外圆磨削表面质量预测方法，具有较高的实用价值。

［1］贾佐诚，陈飞雄，吴诚.硬质合金新进展［J］.粉末冶金工业，2010，20（3）：52－57.

［2］邓朝晖，万林林，张荣辉.难加工材料高效精密磨削技术研究进展［J］.中国机械工程，2008，19（24）：3018－3022.

［3］杜金萍，刘振生，王建民.平面磨削表面粗糙度预测模型的研究［J］.现代制造技术与装备，2007（3）：27－28.

［4］谢红梅，黄伟.基于人工神经网络的磨削表面粗糙度预测研究［J］.精密制造与自动化，2001（4）：30－31.

［5］Timothy J R.Fuzzy Logic with Engineering Applications［M］.Hoboken：John Wiley ＆Sons，Inc.，2004.

［6］张春美.基于粗糙集的自适应神经模糊推理系统的研究和应用［D］.太原：太原理工大学，2005.

［7］段晓燕.基于自适应神经模糊推理系统的迭代学习控制初始控制策略研究［D］.兰州：兰州理工大学，2009.

［8］Taguchi G，Chowdhury S，Taguchi S.Robust Engineering［M］.New York：McGraw－Hill，2000.

［9］Tsai J T，Chou J H，Liu T K.Tuning the Structure and Parameters of a Neural Network by Using Hybrid Taguchi－genetic Algorithm［J］.IEEE Tranctions on Neural Networks，2006，17（1）：69－80.