动载体光电平台角位移精密测量方法研究

李玉龙 何忠波 白鸿柏 郝慧荣 陶 帅 刘树峰

军械工程学院，石家庄，050003

0 引言

动载体光电平台测试技术是近年来发展起来的一门新兴技术，具有机动灵活、实时准确、测量范围广、针对性强等特点。但是由于动载体的振动会使成像仪器产生动态变形，使目标成像像点产生移动，从而导致系统成像质量劣化、成像对比度变差及图像清晰度下降等问题［1］。所以，近年来动载体光电平台隔振技术备受关注，国内外专家学者在这方面做了大量研究，设计了多种形式的动载体隔振装置，但这些隔振装置的设计必须有精密的线位移测试试验设备、尤其是角位移测试试验设备作保障，以检验设计的隔振装置的减振性能及可达到的稳定精度。因此，研制光电平台线位移、角位移的精密测试系统具有重要意义。

对角位移的测试通常采用目标法，用满足要求的分划板作为目标，观察目标成像情况，但此种方法只是定性分析，且人为因素影响较大，无法得到准确的数据；还可以采用编码器法，在被测平台与转台同步的情况下，同时记录平台和转台的数据，计算分析数据可得出稳定精度，但此种方法很难实现两者的完全同步；还有的采用激光自准直测量法，但这种方法需要引入稳定的激光光束，精密半透反射镜等光学设备，成本高，使用较为复杂，仅适合在条件较好的光学实验室使用，不易推广［2－5］。笔者将6个高精度直线微位移传感器安装在平台适当的位置，通过测试传感器放置点一定方向的线位移，推导出平台振动线位移和角位移的测试方法。理论分析表明，该方法简单有效，适用范围广，具有较大的推广价值。

1 光电平台测试系统六自由度位移的理论推导

1.1 坐标系的选择

将光电隔振平台等效成如图1所示模型，从其运动情况分析来看，为测得系统的6个自由度的位移量，需要建立以下几个坐标系：以平台静止时的质心O为原点，与地基固连的惯性坐标系OXYZ，即平台惯性坐标系，该坐标系各轴相对于地基固定不动；以平台质心C为原点，与平台固连的广义坐标系CXPYPZP，即平台固连坐标系，该坐标系相对平台自身坐标系固定；以平台平面一点S为原点，与OXYZ平行的SXSYSZS传感器平面坐标系，三坐标系示意图如图1所示。显然，当物体仅受到重力作用时，OXYZ、CXPYPZP这两个坐标系重合。

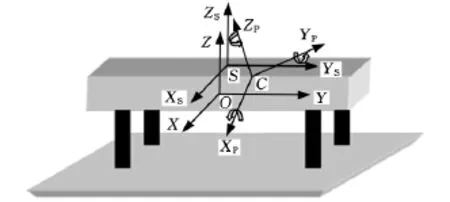
图1 平台坐标系

1.2 方向余弦变换

平台的运动可用平台相对于惯性轴的位移来描述，平台运动后质心C在惯性坐标系中的坐标假设为（xC，yC，zC），刚体绕XP、YP、ZP轴顺次转过α、β、γ，如图2所示。

图2 坐标系变换

不同的坐标系，对应不同的基向量组，不同基之间的坐标变换可通过方向余弦矩阵来建立。假设平台为刚体，如果坐标系间仅是平动，而无转动（α＝β＝γ＝0），则只需要对变量作平移变换，即可测出线位移；若仅绕中心O点转动，且O点与C点重合，顺次绕X、Y、Z三轴转动到XP、YP、ZP的过程可以通过三次分转动实现，每次分转动对应一个方向余弦矩阵（即Aα、Aβ、Aγ），可表示为

连续三次利用转动组合公式，可以得到台体绕三轴转动的方向余弦矩阵A为

若高精度的光电平台隔振系统绕三轴转动的角度α、β、γ非常小，可取近似值cosα≈cosβ≈cosγ≈1，sinα≈α，sinβ≈β，sinγ≈γ。研究小平移和小转动，根据有限转动的交换定理，转动次序是可以交换的，即转动最后位置与转动分量的顺序无关，并且绕平台轴旋转的角度和绕惯性轴旋转的角度是相等的［6］。交换定理体现在数学表达式上就是忽略坐标变换方向余弦阵的高阶项。因此，可以将方向余弦阵简化为

如果物体内有一点M，在惯性坐标系OXYZ中坐标为（xM，yM，zM），在CXPYPZP坐标系中的坐标为（xP，yP，zP），则两者有如下关系：

由于传感器放置于平台上平面，测得的位移变化量是相对于平台平面的值。假设平台上平面与OXYZ坐标系的Z轴交点坐标为S（0，0，h），以S为原点，建立与OXYZ平行的SXSYSZS传感器平面坐标系。要得到平台关于坐标系OXYZ的六自由度位移，首先需要将传感器信号通过平移和余弦转动阵转换到CXPYPZP坐标系中，然后再进行一次坐标平移转换到OXYZ坐标系。还以M 点为例，设M 在SXSYSZS坐标系中的坐标为（xS，yS，zS），则坐标转换方程为

其中，（xC，yC，zC）和α、β、γ 可以通过传感器测得信号变换后得到，h可以通过系统辨识得到，M点在平面坐标系SXSYSZS的坐标（xS，yS，zS）表示M点在平面中的位置，可以通过直接测量M点在平面中相对S点的尺寸得到。

1.3 平台六自由度位移的推导计算

要测得相对于惯性坐标系OXYZ的三轴平动和绕三轴转动位移，6个传感器均安装于平台上平面上（图3）。根据以上分析，首先需要确定6个传感器相对于平台上平面坐标系SXSYSZS及相对于CXPYPZP的位置，然后向广义坐标系OXYZ作平移，从而得出系统相对于固定惯性坐标原点的有效信号值。设坐标系CXPYPZP到SXSYSZS坐标系的六自由度平移量、转动角分别为xPS、yPS、zPS、α、β、γ，其中，Z 轴向上为正，Y 轴指向传感器5方向为正（图3）。

图3 平台系统结构示意图

以传感器Sy1点的坐标为例，其在平台固连坐标系CXPYPZP中的坐标Sy1（xy1，yy1，zy1）和固定惯性坐标系OXYZ中的坐标（x，y，z）间具有如下关系：

（xPS，yPS，zPS）表 示 CXPYPZP上 任 一 点 到SXSYSZS坐标系的平移量，OXYZ与SXSYSZS之间只有Z轴方向上的偏移量h。则坐标系SXSYSZS到坐标系OXYZ的坐标偏移量为

其中，（x0，y0，z0）表示Sy1点在SXSYSZS坐标系中的坐标，当系统处于初始状态下时，可以认为坐标系CXPYPZP与坐标系OXYZ重合，可以认为

由于一般的传感器只能测试一个方向上的线位移，因此每个传感器只能测得δ的一个元素值。将每一个传感器位置坐标代入上述坐标变换方程，就可以得到一个包含相对于坐标系OXYZ的6个未知量的方程，只要6个传感器布置合理，就可以得到不相关的6个方程组，联立求解可得到平台的位移。以第一个传感器位置Sy1点为例，坐标变换关系式中，有效方程只有一个，即

同理，可以得到其余5个传感器位置的位移方程：

其中，Δy1、Δz2、Δy3、Δz4、Δx5、Δz6分别表示各传感器所测得的位移，α、β、γ表示3个转动角度，下标x、y、z表示传感器方向，数字1～6表示传感器序号，包含3个垂直方向和3个水平方向共6个传感器。传感器位置相对于平台固连坐标系的坐标（xP，yP、zP）是固定的，传感器在该坐标系中的位置最直观、最精确，同时也可避免重心偏移带来的运算误差，所以假定坐标系CXPYPZP是“定坐标系”，在该坐标系下传感器Sz2、Sz4、Sz6的坐标分别为（l2x，l2y，lz）、（l4x，－l4y，lz）、（－l6x，－l6y，lz），传感器 Sy1、Sy3、Sx5的坐标 分别为 （－l1x，l1y，lz）、（l3x，l3y，lz）、（l5x，－l5y，lz）。 初 始状态下，相对于OXYZ的传感器坐标与在CXPYPZP中的坐标重合。由以上坐标变换可知，坐标平移会改变刚体中某点相对不同坐标系原点的坐标，但不改变刚体中任意点的位移量和偏转角度。由于OXYZ可以由SXSYSZS平移（0，0，－lz）得到，所以，在任意由OXYZ坐标系平移得到的坐标系中，传感器信号所表示的位置变化量是不变的。在初始情况下，以SXSYSZS为惯性坐标系时，按照以上安装方法，Sx5、Sz2的横坐标为零，所有传感器的Z坐标为零，即

坐标变换时，由于受传感器放置方向的限制，得出的Sy3点相对于惯性坐标系SXSYSZS的位移量与传感器测得信号是反向的，设Sy1、Sz2、Sy3、Sz4、Sx5、Sz6各传感器测试的信号值为S′y1、S′z2、S′y3、S′z4、S′x5、S′z6，那么S′y3＝－Δy3，将式（9）～式（11）联立可得

显然，通过直线位移传感器的信号可测出传感器安装点的位移，可利用式（14）推导得到平台三轴向的线位移和绕三轴转动的角位移。

2 测试系统传感器的选用及安装位置

以某机载光电平台为例进行研究，其要求如下：振动冲击的加速度为5g（20～500Hz）；无角位移减振器三向振动衰减率不小于20dB；最大角位移小于40μrad（曝光时间内）；光学角位移测量系统动态测量精度小于10μrad。由于曝光时间短，振动速度大，测试精度要求高，传感器需要具有宽频带、高精度、高灵敏度的性能。查阅传感器参数可知，中国地震局工程力学研究所研制的2000－2型拾震器，通频带为0.5～1000Hz，测试位移灵敏度为0.01μm，量程为高速时500mm，中速时200mm，低速时20mm，可以满足本系统要求。

2.1 传感器的安装位置分析

由式（14）可知，传感器确定以后，影响系统测试精度的主要因素是传感器信号是否能反映安装点实际位移情况，因此确定传感器安装位置十分重要，应该注意以下几点：

（1）传感器的位置要在信号反应最敏感的地方，也是在测试方向上输出能量最大的点上，不能放置在节点位置，以防止传感器测不到理想信号，甚至测不到信号［7］。

（2）为了减小传感器的测量误差，传感器一般沿X轴和Y轴或垂直于X轴和Y轴方向放置。隔振平台系统广义坐标原点选在平台重心的位置，而重心一般不在测量信号的平台平面上，所以当传感器测量水平、垂直信号及沿X轴和Y轴转动时，传感器位置与平台位置的偏差不会很大。但是，当测量绕Z轴转动的角位移时，由于绕轴的真实位移垂直于测点到原点的直线，要测到真实的绕Z轴的角位移，一般需要将两个传感器对称放置在X轴和Y轴上，如传感器Sy1、Sy3［8］。

（3）为了使传感器的布置尽量不影响平台重心的位置，需要尽可能地在使测试信号较大的同时，将传感器对称布置［9］。

所以，6个传感器的安装位置如图3所示。

2.2 影响系统测试精度的因素与使用范围分析

通过以上分析及推导公式中应用的数据可知，影响系统测试精度的因素主要有：①传感器测试信号的精度，传感器的测试精度越高，系统的测试精度也越高，反之越低［9］；② 尽管理想情况下，系统6个传感器测试数据反映测试点的真实位移，且计算推导时各测试值相互关联，但实际中，由于传感器存在个体差异，所以测试精度必然会受到影响；③传感器采集关于平台平面对称的6个点的位移，安装位置的精度直接决定计算的真实情况，所以应尽量保证传感器安装位置精度；④其他条件相同时，转动角度越小，测试的精度越高（方向余弦近似转化时的近似计算误差越小），所以本测试系统适合微隔振平台，对于角位移较大的隔振平台误差较大。

其中，传感器的个体差异不可避免；传感器放置位置精度越高越好，但误差无法避免。若假设两者都为理想状态，只有传感器的精度和平台转动角度的大小对平台测试精度有影响。选定的传感器测试精度（灵敏度）为0.01μm，以测试绕Z轴转动角度的Sy1和Sy3传感器为例（无绕X轴和Y轴的转动，即α＝β＝0），可以测得的最小位移为0.01μm。由式（12）得

图4 线位移与角位移偏移量关系

3 结语

本文根据某课题对动载体光电平台隔振效果验证的需求，设计了一种用直线位移传感器测试平台动态线位移、角位移的方法，分析了传感器参数与测试系统精度的相互关系。该方法利用刚体动力学的基本原理建立平台惯性坐标系、平台固连坐标系和传感器平面坐标系，再通过坐标变换建立各坐标系的相互关系，推导出传感器测试信号与平台线位移、角位移的关系式。测试时，仅需要测得各传感器的信号值，就可以计算平台的6个自由度的位移，方便有效，操作简单。选用宽频域传感器可实时测试高频率振动下平台的位移参数，对高频振动环境下平台线位移，尤其是角位移的测试有较大的应用价值。

［1］张葆，贾平，黄猛.动载体成像模糊的振动被动控制技术［J］.光学技术，2003，29（3）：281－283.

［2］段志姣，王宇.机载光电系统稳定精度测试方法［J］.光电与光学工程，2008，6（3）：53－56.

［3］杨波，陈就.一种双速同步机轴角位移高精度测量系统［J］.微电机，2010，43（4）：77－79.

［4］乐开端，曹建安，周翔，等.高精度激光测角技术研究［J］.光子学报，2004，33（9）：1108－1110.

［5］王雁，赵忠杰，马社.光电平台微角振动激光探测方法研究［J］.强激光与粒子束，2007，19（1）：40－44.

［6］贾书惠.刚体动力学［M］.北京：高等教育出版社，1987.

［7］刘福强，张令弥.作动器／传感器优化配置的研究进展［J］.力学学报，2000，30（4）：64－69.

［8］张春良.微制造平台振动主动控制研究［D］.杭州：浙江大学，2003.

［9］陶帅.六自由度压电微动平台主动隔振技术研究［D］.石家庄：军械工程学院，2010.