仿生移动机器人并联机构运动学正解的鱼群算法求解

宋孟军 张明路

河北工业大学，天津，300130

0 引言

并联机器人并联机构运动学正解的求解相对困难，且多数情况下正解的存在并不唯一，而并联机器人并联机构运动学逆解的求解相对简单，这与串联机器人串联机构的求解恰好相反，但并联机构运动学正解和逆解的求解，相对于串联机构均要略显复杂，尤其是并联机构运动学正解的求解。并联机构正解的求解暂无统一、有效且较为简便的数值或几何求 解方法［1－2］。赵杰等［3］利用几何方法对Delta并联机器人运动学正解进行了求解，可得到工作空间内满足运动连续性条件的唯一解；文献［4－5］同样利用代数消元和代数几何方法对6－6型Stewart并联机器人和五自由度并联机构进行了运动学正解求解。虽然并联机构的数值求解方法可以求解出并联机构的运动学正解精确解，但是计算过程繁琐，计算结果变量多，存在多解择优等问题。几何求解方法可以通过解算并联机构的几何关系来较为简捷地求解出并联机构的运动学正解，且正解唯一，但几何求解方法一般应用于结构较为特殊的并联机构，缺乏广泛的适应性验证。鉴于此，神经网络、遗传算法、粒子群算法等控制学算法被引入到并联机器人运动学正解的求解中。神经网络算法［6－7］可以避免复杂的公式推导，求解简单，但需借助运动学逆解并利用逆解结果进行训练学习；遗传算法［8－9］能够优化出并联机器人运动学正解的全部实数解，且稳定性较好，但存在过早收敛、收敛速度缓慢等问题；粒子群算法［10－11］能够进行全局优化，且代码易于实现，但容易陷入局部极值、存在进化后期收敛速度放慢等问题；

李晓磊等［12］于2002年提出了以觅食行为、聚群行为、追尾行为和随机行为为特征的鱼群算法，这是一种新型的集群智能算法，能够加快收敛速度，防止局部停滞振荡，并能够跳出局部极值进行全局寻优。在电力系统配电网规划、水资源联合调配、无线传感网络覆盖优化、图像处理等领域［13－17］取得了良好的应用效果。

本文应用空间解析几何方法求解出仿生移动机器人并联机构的解析解，并应用人工鱼群算法对并联机构的运动学正解进行了求解，并对运动学正解结果进行了仿真验证。

1 仿生移动机器人并联机构运动学正解

本文所研究对象为一种具有变形关节的新型多足移动机器人，通过变形关节可以实现多种运动模式，具有较强的地面适应能力，该移动机器人具有6条结构相同的变形轮腿，所以又兼具轮式移动机器人和腿式移动机器人的特点，如图1所示。变形移动机器人腿部为串联机构，具有4个旋转自由度，依据仿生学原理而建立，多腿协调可以模仿多种动物进行运动，因此本文称此种移动机器人为仿生移动机器人，此种机构为仿生移动机构。

图1 多运动模式变形移动机器人腿部模型

与动物运动机理相同，仿生移动机器人在运动时存在摆动腿和支撑腿，摆动腿向前迈进的同时，支撑腿负责支撑并向前移动，此时，所有支撑腿可看作一个并联机构：躯体为动平台，支撑物（如大地）为定平台，并联分支为各支撑腿。

由于3条支撑腿即可维持机体平衡，本文以对称布置于仿生移动机器人机体两侧的3条机械腿为研究对象，作为仿生移动机器人并联机构的3个分支，由于每一分支均为虎克铰—（变异）虎克铰—球面副机构，故3条支撑腿则构成3－TTS并联机构。

1.1 空间机构自由度

图2为3－TTS并联机构的运动螺旋分布图。将变异虎克铰与虎克铰进行数学建模，两者具有相同的数学模型：两转动轴线在空间内正交于一点。

图2 仿生移动机器人并联机构的运动螺旋分布

图2中，上三角代表动平台，为仿生移动机器人机身，下三角代表定平台，为地面，各支链的参考坐标系为OXYZ，固定于定平台上，各支链内的运动螺旋以＄ij表示（i代表第i个支链，j代表第j个运动副），在图2内的3个支链中选择第一个支链的第一个运动螺旋与参考坐标系OXYZ的X轴重合，第二个运动螺旋与Y轴平行，第三个运动螺旋与Z轴平行，各关节点在参考坐标系OXYZ 中的坐标为：A（a1，0，0），B（a2，0，b2），C（a3，0，b3），D（a4，0，b4），则支链1中各运动螺旋在参考坐标系中可以表示为

计算式（1）的约束螺旋可以发现，支链1并不存在约束螺旋系。又因＄15和＄16两运动副平行，所以存在一个冗余自由度。3个分支结构相同，则共存在3个冗余自由度。

当动平台在图3所示位姿下发生有限的转动或移动时，机构的运动螺旋系为

图3 仿生移动机器人并联机构的数学模型构建

计算式（2）可以发现，此时支链1并不存在约束螺旋系，又因＄15与＄16相互平行，所以支链1仍存在一个冗余自由度，3个分支共存在3个冗余自由度。

考虑到图2所示并联机构内各支链自由度数均较多，所以在不影响仿生移动机器人稳定性情况下，动平台发生任意方向的运动，该并联机构都将具有6个自由度，即3个转动和3个移动，并且包含3个冗余自由度，此并联机构共具有9个自由度。

另外，计算空间机构自由度的常用公式还有Kutzbach Grubler公式：

式中，M 为机构的自由度数；n为机构内杆件数；g为运动副的数目；fi为第i个运动副的自由度数。

因机构内公共约束的存在，所以式（3）通常写为

式中，d为机构的阶数；λ为公共约束数。

由于图3所示并联机构没有公共约束，故同样可以利用式（3）计算并得到相同的结果：

1.2 正解模型

3－TTS并联机构的三维模型及坐标系构建情况如图4所示。移动过程中，在所构建的运动学模型基础之上［18-19］，机器人动平台的运动满足零力矩点（ZMP）稳定性判定理论［20］，可对机器人的运动轨迹进行规划，并可同时对当前步态进行规划，使得ZMP轨迹落在满足稳定裕度的稳定区域内，因此可假定A、E、F三支撑点处于瞬时稳定支撑状态，进而可开展机器人运动学正解的求解。

图4 仿生移动机器人并联机构三维模型及坐标系构建

如图4所示，为便于计算，本文将采用相对运动的方法，将定平台设定为机身，动平台设定为地面。起始坐标系（Ox0y0z0）建立在3－TTS并联机构定平台（机身）的几何中心位置。动定平台采用正三角形结构，分别用于连接各分支第一关节和末端关节，并联机构的3个分支采用对称分布，起始坐标系原点与各分支第一关节中心点连线的距离相等，夹角为120°。动平台坐标系原点位于动平台的外接球球心处，即位于图4所示动平台的几何中心处。取AB、BC、CD 三杆长为90mm，定平台外接球的半径为70mm。

求解图4所示下平台O′点位置及下平台姿态即为求解仿生移动机器人并联机构运动学正解问题。

首先，构建图4所示并联机构第一分支的运动学模型，如图5所示。图5所示运动学模型各变量及参数如表1所示。

图5 仿生移动机器人腿部运动学模型构建

表1 仿生移动机器人腿部连杆参数及关节转角变量

依据坐标变换法则，可得关于表1所示各参数的变换矩阵，并求得关于该分支的运动学方程：

3－TTS并联机构其余两分支运动学模型与第一分支的构建方法相同，三分支末端位置的解析解如表2所示。

表2 仿生移动机器人并联机构三分支位置解

仿生移动机器人具有多种运动模式，可将3－TTS并联机构简化为3－TRS并联机构，即依据变形关节的特点，将关节4（Cx4y4z4）固定于某特定运动模式下，保持不变。如图3所示。

图3为3个分支的4个转角变量分别输入参考值0、－π／12、－π／12、π时的数学模型构建图，因3个分支均为独立的串联机构，本例以第一分支作为主动运动机构，而其余两分支作为从动运动机构，即以主从移动机器人协同运动的方式进行3－TRS并联机构运动学正解求解。并以3个分支末端之间的距离为约束条件，建立位置正解的非线性约束方程组如下：

式（8）中，P1、P2、P3为图3所示各分支末端的位置矢量，为已知矢量，P′1、P′2、P′3为运动后各分支末端的位置矢量，因第一分支为主动运动机构，所以P′1为已知矢量，而P′2、P′3为未知矢量。结合已有的约束方程组，运用人工鱼群算法的分解协调优化思路，并进行一定地改进，可对仿生移动机器人并联机构的运动学正解进行求解。

2 算法设计

人工鱼群算法通过模拟鱼群的觅食、聚群、追尾和随机游动等行为实现寻优，具有并行搜索、快速收敛、快速跟踪、算法简单、全局性强等特点［12-13］。人工鱼群的觅食行为是在视域范围内随机移动一步，若食物浓度高于目前位置则向该方向前进一步，若尝试多次后仍没有找到合适位置，则执行随机行为。聚群行为是探索邻域内所有伙伴中心处的食物浓度，若高于目前位置且不拥挤则向该方向前进一步，否则执行觅食行为。追尾行为是探索邻域内食物浓度最大的伙伴，若该伙伴处食物浓度高于目前位置且不拥挤，则向该方向前进一步，否则执行觅食行为。随机行为则是在视域范围内随机移动一步。

随着对象规模和问题复杂程度的增加，人工鱼群算法也暴露出一些不足，例如，当对象数量多、寻优域较大时，容易造成寻优结果不收敛，或容易陷入局部极值，收敛效果不理想。本文将针对仿生移动机器人并联机构的特点对鱼群算法的协调行为进行改进，寻找仿生移动机器人并联机构运动学正解的最优解。

2.1 数学模型

本文目标是寻找满足非线性约束方程组（式（4））的仿生移动机器人并联机构运动学正解的最优解，即

式中，δ为拥挤度因子。

2.2 人工鱼群初始化

式（9）内，已知P′2、P′3两未知矢量所在分支各有3个相互独立的未知变量：

式中，rand（）产生0～1随机数；i为鱼群种类；j为每条人工鱼的3个分量（第4个分量即θ5为常量）；k＝1，2，…，n，为人工鱼数目标号；R 为寻优域；AF（i）jk为人工鱼群，如 AF（1）23表示第1种类鱼群内的第3条人工鱼第2个分量（即原正解表达式内的θ3）；θj为人工鱼初始状态。

2.3 人工鱼群行为描述

人工鱼的觅食、聚群和追尾行为成功均须向前移动一步，AF（i）k表示包含3条人工鱼分量的第i组鱼的第k条鱼：

minAF（c）（）为第c类人工鱼食物浓度，即为式（9）的距离误差，c＝1，2，3。

人工鱼AF（i）的觅食行为描述如下：

（1）引入人工鱼AFk（i），设置尝试搜索的最大次数（Try＿numb er）。

（2）在视域范围内任选两条人工鱼p：

（3）若 minAF（i）（AFp（i））＜ minAF（i）（AFk（i）），则AFk（i）＝AFp（i）；否则继续步骤（2）。

（4）Try＿number次后，执行随机行为：

人工鱼AF（i）的聚群行为描述如下：

（1）设定拥挤度因子δ、δ1、δ2；

（2）同时判定两条鱼邻域内的伙伴数目，t、k表达意义如前：

（3）满足步骤（2）的伙伴数目n＿F：n＿F←n＿F＋1。

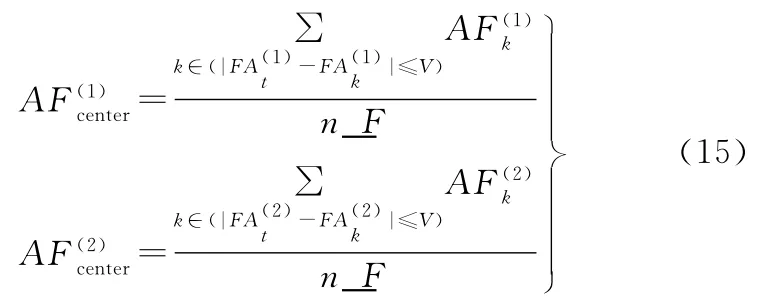
则两条鱼分别向中心位置前进一步：

否则执行觅食行为。

人工鱼AF（i）的追尾行为描述如下：

（1）从满足｜AFt（i）－AFk（i）｜≤V内的人工鱼中，选 出 minAF（i）（AFk（i））最 小 的 人 工 鱼k＝min，选择过程内，人工鱼须同时满足：

（2）将步骤（1）选出的最小值写入公告板B（i）：

则两条鱼均向k＝min位置前进一步：

否则执行觅食行为。

2.4 算法描述

人工鱼群算法流程如图6所示。

图6 算法流程图

（1）构造数学模型，输入人工鱼初始状态θj，设定视域V，步长S，拥挤度因子δ、δ1、δ2，寻优域R。

（2）设定人工鱼规模n、搜索次数Try＿num ber、初始化人工鱼群FA（i）。

（3）初始化公告板B（c），B（c）为c类人工鱼群的公告板：

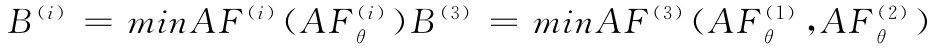
（4）对每组两条人工鱼AF（i）k进行计算：

式（19）为协调函数。

（6）循环次数：n＿for←n＿for＋1。

（7）公告板：B（c）＝ minAF（c）。

（8）迭代次数：n＿while←n＿while＋1。

（9）将 每 次 迭 代 获 取 的 公 告 板 B（c）输出，结束。

寻优域R与视域V 相同时，适当选取步长S，可获得更高的食物浓度minAF（i）（）。

2.5 仿真实现

基于MATLAB仿真实现了本文仿生移动机器人并联机构运动学正解的求解。在如图3所示仿生移动机器人并联机构数学模型上应用改进后的鱼群算法，对并联机构运动学正解进行描述，结果如图7～图14所示。

从图7、图8可以看出，尽管迭代起始处距离误差较大，但是随着迭代开始，两类鱼群（AF（i））均能够快速寻优，因为鱼群寻优的目标是距离误差最小化，食物浓度minAF（i）（）须趋近于0。

图7 鱼群1寻优

图8 鱼群2寻优

图9表明，协调函数值能够在拥挤度因子δ1、δ2规定范围内波动，因为AF（i）在寻优过程中不仅考虑了两类鱼是否满足同时寻优，而且引入协调函数，从而使并联机构运动学正解不断接近数学模型式（5）下的最优。

图9 协调寻优

从图10～图13可以看出，除少数鱼群聚集在局部极值之外，大多数鱼群均能聚集于全局极值，这是因为AF（i）在聚群和追尾过程中充分考虑了拥挤度因子δ的选择，在寻优过程中同时满足两类鱼群的视域、食物浓度和协调函数，使得两类鱼群逐渐向共同的优化目标移动。

图14表明，AF（i）所寻优的结果可以达到仿生移动机器人并联机构运动学正解的求解精度要求，因为人工鱼群AF（i）初始搜索范围在寻优域R内，且视域V＝R，所以在步长S适当时，人工鱼群AF（i）在觅食过程中增加了搜索全局极值的可能性，在聚群行为和追尾行为的作用下能够跳出局部极值寻优并加速向全局极值移动。

图10 鱼群1初始状态

图11 鱼群1聚集

图12 鱼群2初始状态

图13 鱼群2聚集

图14 寻优最终并联机构运动学正解

由图3与图14所示各分支末端位置解可知，鱼群算法所求正解误差与拥挤度因子的选取有关，本例中拥挤度因子δ、δ1、δ2分别为1.00、1.01、0.99。

如图14所示，满足式（5）的正解最优解分别为：0.0074mm，0.0024mm，364.5556mm（初始值为363.5152mm），迭代次数为100次，所求最优解可以满足仿生移动机器人运动精度要求。

由图7～图14所示仿真结果可知，增加并联机构的分支数，例如由目前三分支增加至六分支，合理分布于机身两侧，并利用文中1.2节所述运动学正解模型构建方法，对六分支并联机构的运动学正解模型进行构建，即对六足仿生机器人的运动学正解模型进行构建，通过增加式 （4）位置正解的非线性约束方程组数目，同理应用鱼群算法可对六分支并联机构的运动学正解模型进行求解。

3 结论

（1）对一种多运动模式仿生移动机器人并联机构进行简化，并运用螺旋理论计算该并联机构的自由度。

（2）应用坐标变换法则对仿生移动机器人并联机构的运动学正解模型进行构建，可同时构建仿生移动机器人并联机构的三维模型和该机构运动学正解的数学模型。

（3）提出了基于寻优域、视域、拥挤度因子等改进后的鱼群算法，构建了鱼群算法的数学模型，引入了协调函数，对鱼群算法进行描述。

（4）仿真实现鱼群算法，结果表明，代码易于实现，运用鱼群算法对并联机构的运动学正解进行求解，无需逆解，无需初值，且具有较好的全局寻优，快速寻优性能。

［1］Jamwal P K，Xie S Q，Tsoi Y H，et al.Forward Kinematics Modelling of a Parallel Ankle Rehabilitation Robot Using Modified Fuzzy Inference［J］.Mechanism and Machine Theory，2010，45（11）：1537－1554.

［2］Li M，Huang T，Chetwynd D G，et al.Forward Position Analysis of the 3－DOF Module of the TriVariant：A 5－DOF Reconfigurable Hybrid Robot［J］.Journal of Mechanical Design，Transactions of the ASME，2006，128：319－322.

［3］赵杰，朱延河，蔡鹤皋.Delta型并联机器人运动学正解几何解法［J］.哈尔滨工业大学学报，2003，35（1）：25－27.

［4］Lee Tae－Young，Shim Jae－Kyung.Forward Kinematics of the General 6－6Stewart Platform Using Algebraic Elimination Original Research Article［J］.Mechanism and Machine Theory，2001，36（9）：1073－1085.

［5］Masouleh M T，Gosselin C，Husty M，et al.Forward Kinematic Problem of 5－RPUR Parallel Mechanisms （3T2R）with Identical Limb Structures［J］.Mechanism and Machine Theory，2011，46（7）：1－15.

［6］张世辉，孔令富，原福永，等.基于自构形快速BP网络的并联机器人位置正解方法研究［J］.机器人，2004，26（4）：314－319.

［7］Parikh P J，Lam S S Y.A Hybrid Strategy to Solve the Forward Kinematics Problem in Parallel Manipulators［J］.IEEE Transactions on Robotics，2005，21（1）：18－25.

［8］Jamwal P K，Xie Shengquan，Kean C A.Kinematic Design Optimization of a Parallel Ankle Rehabilitation Robot Using Modified Genetic Algorithm［J］.Robotics and Autonomous Systems，2009，57（10）：1018－1027.

［9］贺利乐，刘宏昭，王朋，等.基于改进遗传算法的六自由度并联机器人位置正解研究［J］.应用科学学报，2005，23（5）：522－525.

［10］Montalvo I，Izauierdo J，Pérez R，et al.Particle Swarm Optimization Applied to the Design of Water Supply Systems［J］.Computers and Mathematics with Applications，2008，56（3）：769－776.

［11］车林仙，何兵，易建，等.对称结构Stewart机构位置正解的改进粒子群算法［J］.农业机械学报，2008，39（10）：158－163.

［12］李晓磊，路飞，田国会，等.组合优化问题的人工鱼群算法应用［J］.山东大学学报（工学版），2004，34（5）：64－67.

［13］Ravinda K，Ahuj A，Ozlem E，et al.A Survey of Very Large－scale Neighborhood Search Techniques［J］.Discrete Applied Mathematics，2002，123（1／3）：75－102.

［14］张秋亮.鱼群算法在配电网规划中的应用研究［D］.保定：华北电力大学（保定），2008.

［15］高玉芳，张展羽.混沌人工鱼群算法及其在灌区优化配水中的应用［J］.农业工程学报，2007，23（6）：7－11.

［16］刘彦君.鱼群算法及在无线传感器网络覆盖优化中的应用［D］.济南：山东大学，2009.

［17］张赫，徐玉如，万磊，等.水下退化图像处理方法［J］.天津大学学报，2010，43（9）：827－833.

［18］Lacagnina M，Muscato G，Sinatra R.Kinematics，Dynamics and Control of a Hybrid Robot Wheeleg［J］.Robotics and Autonomous Systems，2003，45：161－180.

［19］Chen Li，Ma Shugen，Wang Yuechao，et al.Design and Modelling of a Snake Robot in Traveling Wave Locomotion［J］.Mechanism and Machine Theory，2007，42（12）：1632－1642.

［20］Ha Taesin，Choi Chong－Ho.An Effective Trajectory Generation Method for Bipedal Walking［J］.Robotics and Autonomous Systems，2007，55（10）：795－810.