RTCP算法中无碰刀轴矢量的确定

章永年 赵东标 陆永华 刘 凯

南京航空航天大学，南京，210016

0 引言

在多坐标加工中，由于受旋转运动的影响，机床各轴线性插补的合成运动会使实际刀位运动偏离编程直线，该误差称为非线性加工误差［1－2］。非线性误差控制方法主要有刀触点偏置法、线性加密法［3］、自 适 应 线 性 化 法［1］和 RTCP（rotation tool center point）算法［4－5］。其中前三种方法都是在后置处理中对刀位数据进行控制，当刀具磨损或刀具长度变化时必须重新通过后置处理生成数控程序，效率低下。而RTCP算法可保证插补点始终位于编程轨迹上，有效减小了非线性误差。

RTCP算法使得编程坐标直接针对刀具中心而不是坐标的转动中心（头中心）。传统算法要求机床的转轴中心长度正好等于后置处理所考虑的数值，任何修改都要求重新生成程序。集成RTCP算法的数控系统可以直接编写刀具中心轨迹程序，而不用考虑转轴中心长度。国外的一些高档数控系统如FANUC、SIEMENS、FIDIA和NUM数控系统中已具备了RTCP功能，但是其核心算法是保密的。

目前，国内对RTCP算法的研究还处于起步阶 段。 赵 薇 等［5］、Fan 等［6］设 计 了 一 种 集 成RTCP功能的插补算法，减小了非线性误差，但刀轴矢量采用线性插补法：插补过程中刀轴矢量始终位于首末向量所决定的平面内。由于刀轴矢量与旋转轴角度成非线性关系，刀轴矢量线性插补法得到的头中心旋转轴角速度可能超限。耿聪等［7］提出的大圆弧插补法也有类似的不足。因此本文提出了基于旋转轴线性插补的RTCP算法，保证了旋转轴的角速度限制条件，然而在实际加工过程中会出现相邻刀位点在无碰区域内而插补时刀具发生干涉的现象。国内外学者对多轴数控加工中的干涉检测算法进行了大量研究［8－11］，但多注重于给定刀具姿态下的干涉问题，对刀具运动过程中，尤其是集成RTCP功能的全局干涉问题还尚未涉及。

鉴于此，本文详细分析了基于旋转轴线性插补的RTCP算法机理、RTCP算法插补过程中干涉现象产生的原因，最后给出了具体的解决方案。

1 RTCP算法

对于五轴数控加工来说，从输入加工模型到电机运动，中间一般经过刀触点计算、刀轴矢量确定、后置处理和数控插补几个步骤。其中，刀触点计算模块将输入模型按照一定的精度要求离散成一系列的路径点，刀轴矢量确定模块获取各刀触点的无碰最优刀轴矢量，后置处理模块根据机床运动关系生成由许多微线段构成的数控程序，数控插补模块调用线性插补算法输出脉冲或其他信号控制电机运动。刀触点计算模块和刀轴矢量确定模块统称为前置处理模块，该模块在计算刀位点时假定了相邻刀位点之间的运动轨迹为直线段这样一个前提条件。后置处理生成的数控程序针对的是头中心坐标，图1中的Ps、Pe为刀位点，Pos、Poe为头中心。采用线性插补算法插补Pos、Poe时，头中心的运动轨迹为直线，由于旋转轴的加入，相邻刀位点之间的运动轨迹不一定为直线，这样就产生了非线性误差，如图1中的期望插补轨迹与实际插补轨迹不重合。

图1 传统算法示意图

（1）后置处理。设前置处理模块得到的刀位数据为（P，u），以AB双摆头机床为例，单位刀轴矢量u可通过工件坐标系上z轴单位矢量k＝（0，0，1）T旋转变换M ＝rot（Y，φ）·rot（X，θ）得到，即u（θ，φ）＝Mk，其中

这样可以得到刀位点的五轴坐标（P，θ，φ），其中旋转轴坐标由下式确定：

（2）线性插补。通过后置处理得到刀位点坐标后，需要将其转换为数控程序送入数控系统中加工。设直线段起点和终点的坐标为（Ps，θs，φs）、（Pe，θe，φe），线性插补方程为

其中，系数t1∈ ［0，1］。

笔者基于重力异常反演研究的基础上，对与概率成像技术进行设置模型，给予MATLAB程序将其实现，该成像算法具有方法简单，位场分离后异常概率成像分辨率高，抗噪性能强等特点。主要总结一下四个方面。

（3）坐标变换。线性插补得到粗插补刀具中心坐标后，需要计算相应的头中心坐标（Po，θo，φo）：

式中，Lo为刀具中心点到头中心之间的距离。

（4）速度校核。集成RTCP功能后，刀具中心的进给速率F等于编程速率f，而合成的头中心进给速率Fo可能会大于F。如果Fo太高，则控制系统需要限制它，使之不超出允许的最大进给速率。

经过以上步骤得到的刀位点运动轨迹与期望运动轨迹重合，非线性误差减小了，如图2所示。

图2 RTCP算法示意图

2 RTCP插补过程中的干涉现象

RTCP算法为五轴数控系统减小了非线性误差，然而由于旋转轴的存在，RTCP算法在插补过程中刀杆末端的运动轨迹偏离了球面大圆，这样有可能出现干涉现象。

图3 RTCP线性插补过程中发生干涉

不失一般性，下面以直线段起点和终点坐标分别为（Ps，θs，φs）、（Pe，θe，φe）为例计算 RTCP线性插补过程中的刀杆偏差e。

2.1 刀杆偏差e的确定

其中，θ（t）、φ（t）为t 时刻 的 旋转 坐 标，由下式确定：

进一步将相应坐标代入式（7），有

插补偏差为曲线PE（t）与PA（v）的最大法向差，对于只有旋转运动的情况即为图3中的e，然而e的求取比较困难，可采用连接两曲线中点的直线段长度来近似表示。即

将式 （1）、式 （5）、式 （6）、式 （8）代 入 式（10）可得

式中，η为刀杆偏差系数。

对于式（11），有

注意到e（θs，θe，Δφ）＝e（－θe，－θs，Δφ）＝e（θe，θs，Δφ）＝e（θs，θe，－Δφ），即函数e（θs，θe，Δφ）关于θs＝－θe、θs＝θe、Δφ＝0对称。

2.2 RTCP无碰区域的计算

考虑到RTCP插补过程中，实际的插补曲线与刀杆末端最短曲线（测地线）偏移了一定的距离e，为了避免全局干涉，确定无碰区域时，将无碰区域边界线C收缩ke（k为安全系数，k≥1）得到C′，以C′包围的区域R′作为新的无干涉区域，并以此确定刀轴矢量，则在插补过程中将不会发生干涉现象，如图3所示。

综上所述，要想应用RTCP算法，除了后置处理和数控插补与传统算法有所不同外，在确定无碰刀轴矢量时也有一定差异。表1给出了RTCP算法与传统算法的不同点。

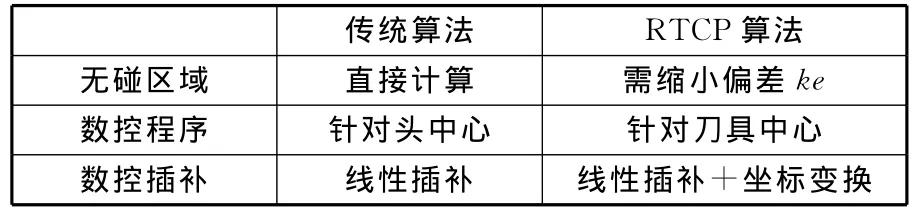
表1 算法比较

3 仿真实例

为了验证算法的有效性，进行了如下的仿真实验。

（1）RTCP插补实验。对表2中的相邻刀位点坐标分别采用传统算法和RTCP算法进行线性插补，仿真结果如图4、图5所示。比较两图可以得出结论，RTCP算法保证了相邻刀位点之间的运动轨迹为直线段，减小了非线性误差。

表2 刀位点坐标

（2）插补偏差仿真实验。由式（11）绘制给定Δφ＝50°下的η－（θs，θe）函数关系曲线如图6所示。从图6可以看出，偏差系数η关于直线θs＝－θe和θs＝θe对称，ηmax存在于θs或θe为最大／小值处。不同Δφ下的η－（θs，θe）关系图与图6类似，只是幅值有所不同，计算不同Δφ下的ηmax，绘制曲线如图7所示。从图7可以看出，ηmax随着Δφ的增大而增大。

图4 传统算法插补图

图5 RTCP算法插补图

图6 η－（θs，θe）函数关系图

图7 ηmax－Δφ函数关系图

（3）RTCP插补无碰刀轴矢量实验。待加工的整体叶轮如图8所示，其中一刀位点的刀杆末端轨迹如图9所示，通过计算得到的无碰区域为无碰边界1包围的区域，图中A、B两点为相邻刀位点的刀杆末端位置，采用式（1）～ 式（4）进行RTCP插补得到的插补曲线超过了无碰区域，发生了干涉。将无碰边界1内缩ke后得到RTCP算法的无碰边界2，将B点移至无碰边界2包围的无碰区域内重新插补则不会发生干涉现象。

图8 整体叶轮

图9 RTCP插补过程中干涉仿真图

4 结语

为了减小非线性误差，本文提出了基于旋转轴线性插补的RTCP算法，并就该算法在插补过程中出现的干涉现象进行了深入的理论分析，仿真实验表明Δφ很大时必须考虑插补过程中刀杆末端偏差。仿真结果证实了算法的可行性。

［1］周艳红，周济.五坐标数控加工的理论误差分析与控制［J］.机械工程学报，1999，35（5）：54－57.

［2］吴大中，王宇晗，冯景春，等.五坐标数控加工的非线性运动误差分析与控制［J］.上海交通大学学报，2007，41（10）：1608－1612.

［3］王丹，陈志同，陈五一.五轴加工中非线性误差的检测和处理方法［J］.北京航空航天大学学报，2008，34（9）：1003－1006.

［4］郑飂默，林浒，张晓辉，等.基于实时插补的五轴加工非线性误差控制［J］.小型微型计算机系统，2010，31（7）：1389－1392.

［5］赵薇，高春，马跃，等.通用RTCP算法的研究与设计［J］.小型微型计算机系统，2008，29（5）：980－984.

［6］Fan S T，Yang W P，Dong C J.RTCP Function in Five－axis Machining［J］.Key Engineering Materials，2011，464：254－259.

［7］耿聪，于东，张晓辉.五轴联动数控加工中的刀具轨迹控制算法［J］.中国机械工程，2010，21（24）：2904－2909.

［8］Lee Y S，Chang T C.2－phase Approach to Global Tool Interference Avoidance in 5－axis Machining［J］.Computer－Aided Design，1995，27（10）：715－729.

［9］Ho S，Sarma S，Adachi Y.Real－time Interference Analysis Between a Tool and an Environment［J］.Computer－Aided Design，2001，33（13）：935－947.

［10］Oleg I，Gershon E，Dan H，et al.Precise Global Collision Detection in Multi－axis NC－machining［J］.Computer－Aided Design，2005，37（9）：909－920.

［11］Ron W，Gershon E.Continuous Path Verification in Multi－axis NC－machining［J］.International Journal of Computational Geometry and Applications，2005，15（4）：351－377.