超球体平方根平淡卡尔曼滤波及其应用

王跃钢，蔚 跃，雷堰龙，陈苏邑

（解放军第二炮兵工程大学自动化系，陕西 西安 710025）

0 引言

初始对准对于惯导系统的精度与启动准备时间有着直接的关系，所以一直被看作惯性导航技术领域的重要问题之一［1］。捷联惯导系统（strap－down inertial navigation system，SINS）初始对准的实质就是确定载体坐标系到真实导航坐标系的转换矩阵。由于初始对准误差将严重影响系统的整体误差，因此要求初始对准的对准精度要高，对准时间要短。采用卡尔曼滤波是实现惯导系统自对准的有效途径之一，但卡尔曼滤波使用的条件是只能用于线性系统，对于非线性系统常用的方法是采用扩展卡尔曼滤波（extended kalman filter，EKF），而在大方位失准角情况下，这种近似线性化的方法舍弃了非线性函数的高阶项，引入了误差，使滤波结果为次优，甚至导致滤波发散［2］。Julier［3］等人从非线性均值和方差传播的角度提出平淡卡尔曼滤波（unscented kalman filter，UKF），这种方法直接利用非线性模型进行递推估计，避免了线性化误差的引入且递推估计过程不需计算矩阵，但随着状态空间维数的增加，计算量也会急剧增大，加重系统计算负担，同时无法保证在滤波更新阶段生成的状态协方差阵非负定［4］，从而直接影响采样点生成时进行的Cholesky分解。为此，本文提出超球体平方根平淡卡尔曼滤波方法，解决上述问题。

文章第一、二章为基础铺垫，第三章将超球体采样及平方根滤波结合提出一种新的滤波方法，并应用到捷联惯导系统大失准角下的非线性误差模型中，第四章通过matlab数值仿真，分别与EKF和UKF进行了对比，说明了新方法的可行性。

1 捷联惯导系统非线性误差方程

1.1 速度误差方程

式中，W为量测噪声，B为噪声驱动阵。

大失准角下的速度误差方程为［5］：

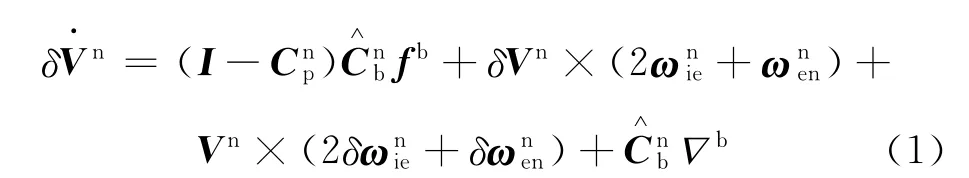
令欧拉失准角φx，φy，φz的转动顺序为φz、φx、φy。则可求得C由式（2）确定：

1.2 姿态误差方程

大失准角下姿态误差方程为［5］：

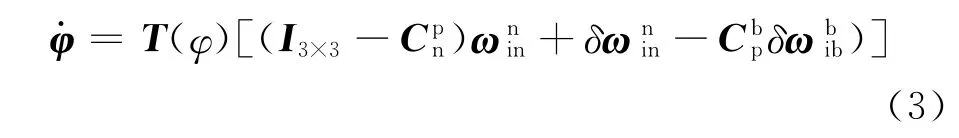
1.3 非线性对准滤波模型

假设陀螺和加速度计误差仅由常值漂移εb＝［εbxεbyεbz］T，▽b＝ ［▽bx▽by▽bz］T和观测噪声εg＝ ［εgxεgyεgz］T，▽r＝ ［▽rx▽ry▽rz］T组成，忽略其他因素的影响，可以表示为：

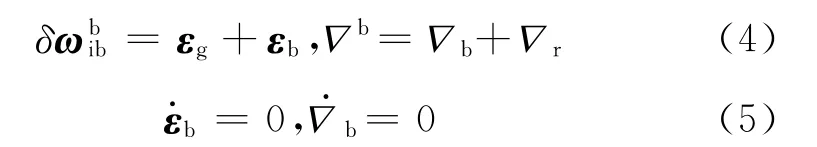
选取状态变量为：

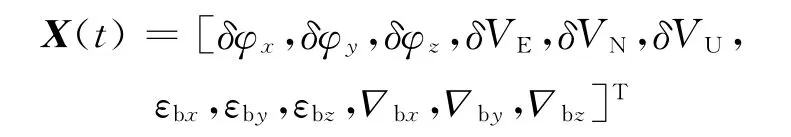
式（1）、式（3）、式（5）组成了大失准角下SINS误差状态方程。

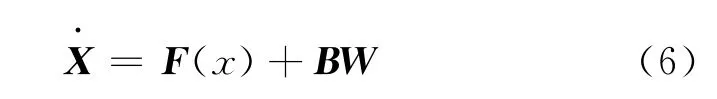
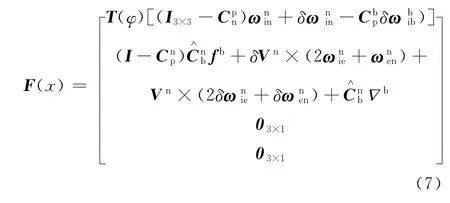
取速度误差为观测量得到SINS观测方程为：

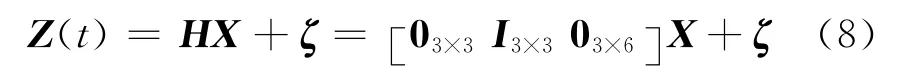
式（8）中，ζ为观测噪声。

式（6）、式（8）构成了非线性对准的滤波模型。

2 超球体采样及平方根滤波

2.1 超球体分布采样点变换方法

Julier等人［3］从非线性均值和方差传播的角度提出UKF，这种方法直接利用非线性模型进行递推估计，避免了线性化误差的引入，且递推估计过程不需计算矩阵，比EKF更为简单，后来又提出了超球体分 布 采 样 点 变 换 （spherical simplex unscented transformation，SSUT）方法［6］，减少采样点的求取，将采样点数目由2n＋1减小到n＋2，当系统维数很大时可以极大地降低计算量［7］。同时SSUT中采样点具有与状态相同的前二阶矩。SSUT采样点的选取步骤如下：

1）选择第0个权值W0，并且0≤W0≤1

2）计算其他权值

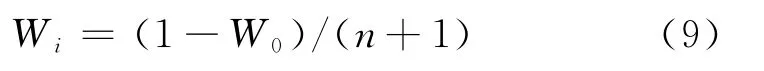
3）初始化一维化状态序列

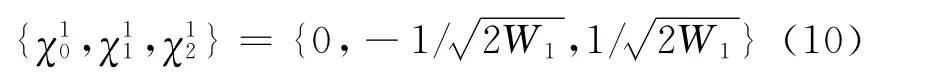
4）空间维数j＝2，3，…，n时，递推公式为：

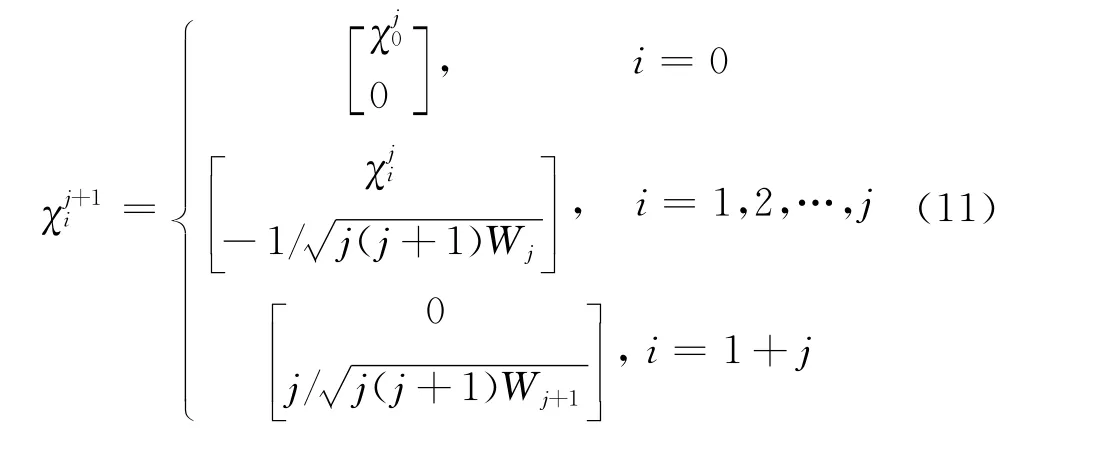
2.2 平方根平淡卡尔曼滤波算法

由于在标准UKF滤波状态更新阶段，P阵很容易失去正定性［8］。造成协方差阵P 无法进行Cholesky分解，不能生成采样点。采用平方根平淡卡尔曼滤波解决此问题，该方法在UKF滤波的时间更新和量测更新阶段采用平方根滤波将状态估计误差协方差阵的Cholesky因子形式Sa直接传递，避免了在采样点计算时对状态估计误差协方差阵的Cholesky分解，从而解决了UKF数值不稳定性的问题，减小了计算量。

3 超球体平方根平淡卡尔曼滤波算法

改进的平淡卡尔曼滤波算法是SSUT方法与平方根UKF结合的方法，这里称之为超球体平方根平淡卡尔曼滤波算法，取超球体采样的首字母以及平方根的第二个字母，该算法英文缩写为SRUKF（spherical root unscented kalman filter）。

不妨设非线性系统的模型如式（13）：

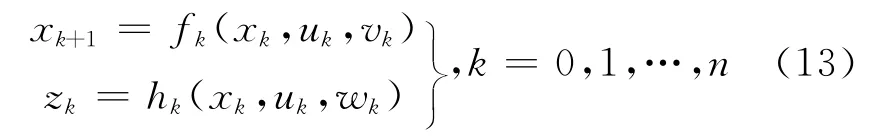
式中，过程噪声wk是均值为0，方差为Q的高斯白噪声。同样，量测噪声vk为均值为0，方差为R的高斯白噪声。

1）初始化

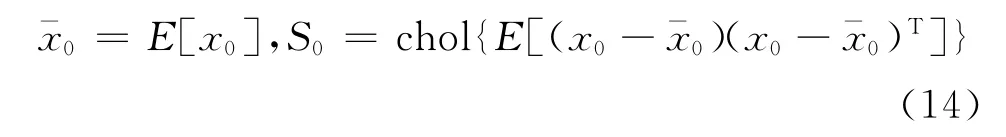
2）计算采样点

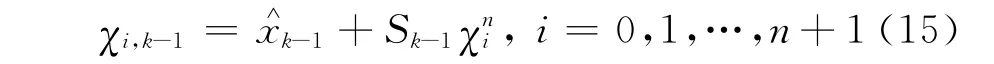
3）时间更新

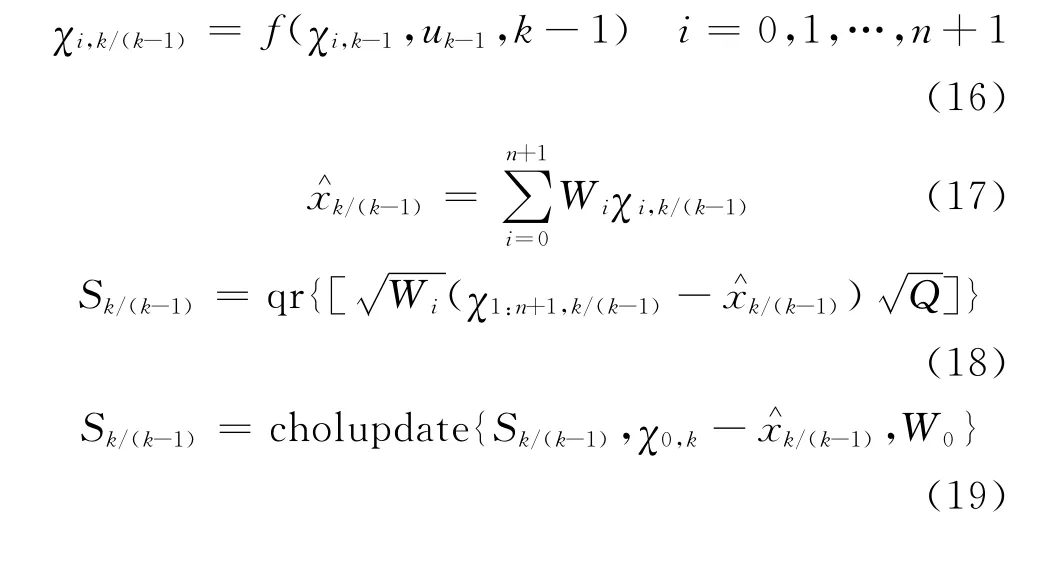
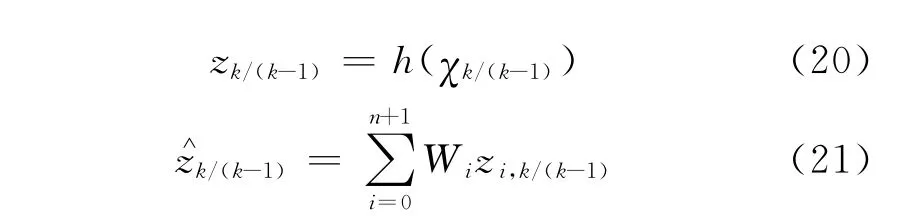
4）量测更新

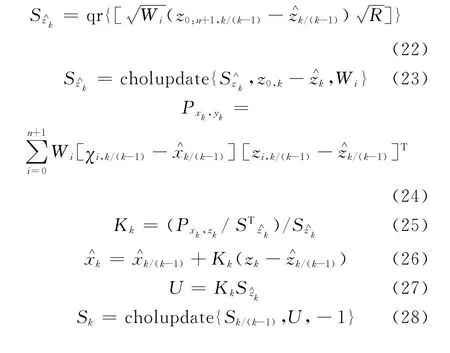
4 仿真分析

仿真初值按照如下选取：东向、北向、天向失准角分别取2°，2°，15°；陀螺常值漂移取0.02 （°）／h，随 机 漂 移 为 0.01 （°）／h；加 速 度 计 常 值 漂 移 为1×10－4g，纬度取45°，当地高度350m，仿真时间400s，SINS采样周期取0.05s。

按照以上仿真条件分别进行EKF，SRUKF，UKF滤波，仿真结果如表1和图1—图3所示。

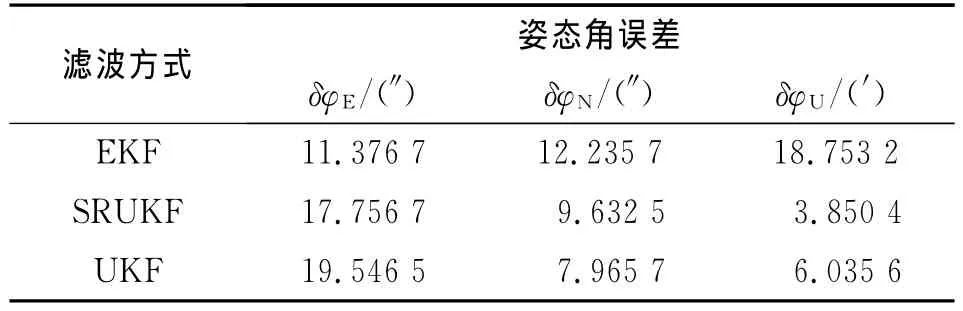
表1 捷联惯导系统的初始对准稳态均值Tab.1 Steady state mean of SINS initial alignment

其中，表1稳态均值是250～350s仿真结果取绝对值后的均值。这段时间内，滤波进入稳态没有了符号的变化，为了比较稳态值偏移0的距离，因此都取绝对值，100s时间段内求均值的目的是为了有效地克服单个奇异点带来的影响，不会对仿真结果造成影响。

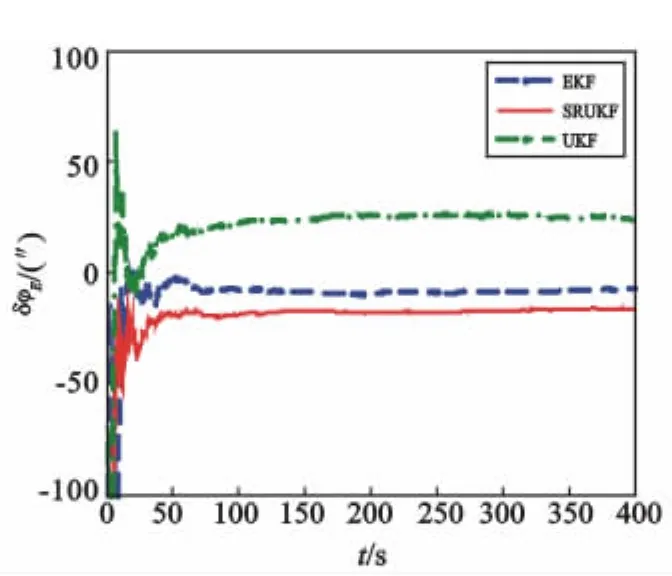
图1 东向误差角估计值Fig.1 Error estimation of east angle

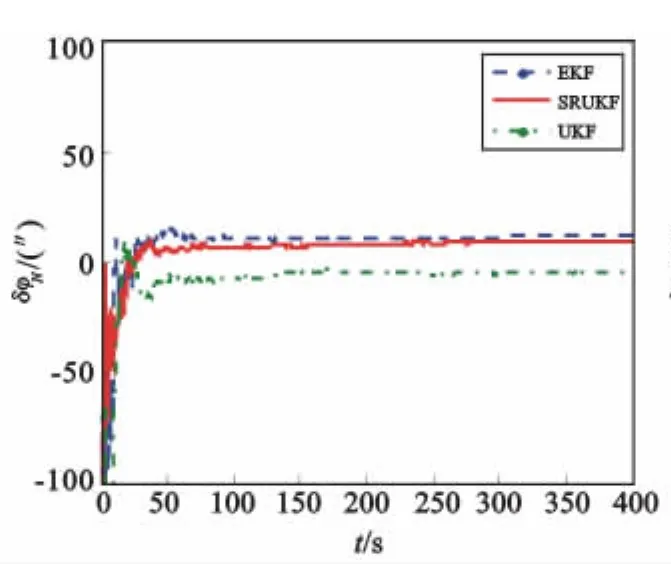
图2 北向误差角估计值Fig.2 Error estimation of north angle

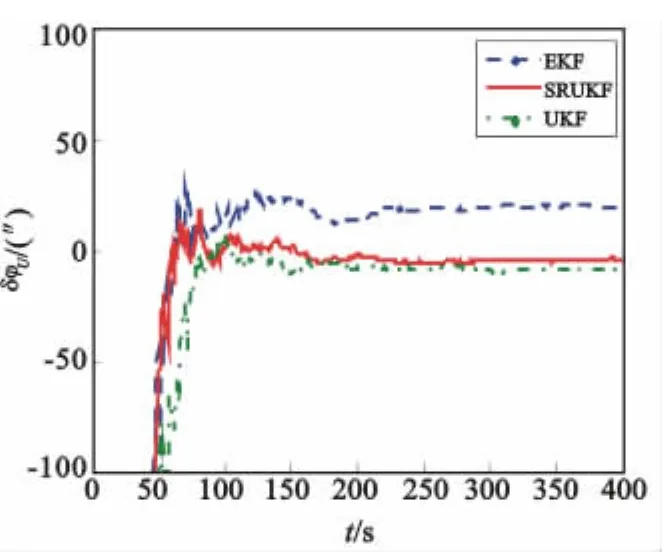
图3 天向误差角估计值Fig.3 Error estimation of attitude angld

捷联惯导系统在该初始条件下水平（东向与北向）误差角的理论稳态误差值为18.73″，天向理论稳态误差值为4.46′。仿真结果表明：水平误差角仿真结果与理论分析的效果相符，三种滤波方法水平失准角误差很小，收敛时间也很快，这是因为水平失准角是小角度。其次，对于初始对准的核心部分方位角的对准精度而言，表1指出SRUKF与UKF的滤波结果相对于EKF来讲与理论值更为接近，这从图3也可以直接看出，这是因为SRUKF和UKF在处理非线性系统的精度能达到二阶，而EKF在处理非线性问题上是按照泰勒级数展开取一阶的线性化方法，其精度只能达到一阶，要想达到更高精度就必须得求复杂的雅克比矩阵。因此，雅克比矩阵的求取是限制EKF精度的主要因素。最后，图3中SRUKF的收敛时间要比UKF快，原因是采样点数目由2n＋1减小到n＋2，系统维数较大时可以减小计算量。综上可知，SRUKF相对于EKF提高了滤波精度，相对于UKF缩短了对准时间，这种改进的方法提高了对准效率。

5 结论

提出了超球体平方根平淡卡尔曼方法，该方法是通过SSUT与平方根滤波结合，解决了UKF数值不稳定性的问题，同时当系统维数较大时降低了计算量。将超球体平方根平淡卡尔曼滤波方法应用到SINS大失准角下的初始对准当中，仿真结果表明：SRUKF对于EKF能有效提高方位失准角对准精度，由18.75′提高到了3.85′；相对于 UKF虽然精度差不多，但是减少了采样点，减小了计算量，提高了计算效率，是一种理想的滤波方法。

［1］邓正隆.惯性导航原理［M］.哈尔滨：哈尔滨工业大学出版社，1994.

［2］李涛.非线性滤波方法存导航系统中的应用研究［D］.长沙：国防科技大学，2003.

［3］Hovland G E，Von Hoff T P，Gallestey E A.Nonlinear estimation methods for parameter tracking in power plants［J］.Control Engineering Practice，2005（13）：1 341－1 345.

［4］NING Xiaolin，FANG Jiangcheng.An autonomous celestial navigation for LEO salellite based on unscented kalman filter and information fusion［J］.Aerospace Science and Technology，2007（11）：222－228.

［5］龙瑞，秦永元，赵长山.简化SPKF在捷联惯导系统非线性对准中的应用［J］.压电与声光，2010，32（5）：746－749.LONG Rui，QIN Yongyuan，ZHAO Changshan.Application of simplified SPKF in non－linear alignment of SINS［J］.Piezoelectrics ＆ Acoustooptics，2010，32（5）：746－749.

［6］Julier S J，Uhlmann J K.Reduced sigma point filters for the propagation of means and covariance through nonlinear transformations［C］／／AACC Proceedings of American Control Conference，2002：887－892

［7］Simon J Julier.The spherical simplex unscented transformation［J］.Proceddings of the IEEE American Control Conference，Denver Colorado，2003：2 430－2 434

［8］SONG Qi，HAN Jianda.An adaptive UKF algorithm for the state and parameter estimations of a mobile robot［J］.Acta Automatica Sinica，2008，34（1）：72－79.